Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

17.2 Causes of Flow Instabilities 503

T( ) = T -

= z +

= z

T( )

Temperature

distribution

for

γ γ

Fig. 17.7 Stability of temperature distribution in the atmosphere



)





)



κ−1





κ−1

, (17.11)

where T



and (T



)

are the ﬂuid-element temperature and P



and (P



)

represent the corresponding pressures at the considered heights.

From (17.11) one obtains

d(ln T



κ − 1

d(ln P ). (17.12)

From (17.9), it follows that

d(ln P )=−

(17.13)

so that the following diﬀerential equation holds:

d(ln T



)=−

κ − 1

. (17.14)

From T = T



1 −



, it follows that

dT = −

= −γ dx

. (17.15)

From (17.14) and (17.15), one obtains



= −

κ − 1

γ

. (17.16)

On introducing the adiabatic temperature gradient, common in meteorology:



κ − 1



(17.17)

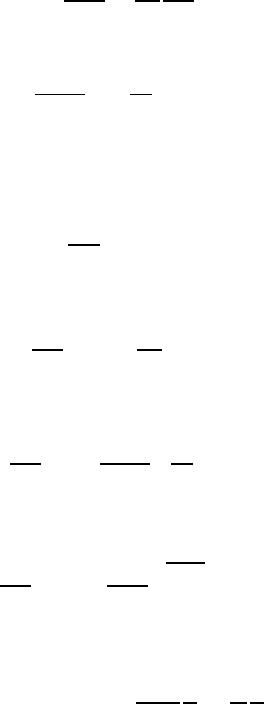
504 17 Unstable Flows

into the above relationship, one can then write



(17.18)

or integrated:



)





(γ

/γ)

. (17.19)

Due to the deﬂection of the ﬂuid particle from position z, where it was in

equilibrium with its surroundings, a ﬂuid motion results due to the presence

of the buoyancy force, for which the following equation of motion holds:



=(ρ − ρ



) g (17.20)

or, after further rewriting:

= g







− 1



. (17.21)

Thus, because (T



)

= T

, (17.21) holds:

= g





)





− 1



(17.22)

and thus one can write for the subsequent considerations

= g

⎡

⎣



T (z)



−γ

− 1

⎤

⎦

. (17.23)

For these considerations, it is important to know whether the existing linear

temperature gradient γ = T

/c is larger or smaller than the adiabatic temper-

ature gradient of the atmosphere, i.e.

(κ−1)

≡

γ decides the stability

of the temperature distribution in the atmosphere.

Hence, the following considerations can be carried out:

• A positive deﬂection z causes T (z) <T

because T = T

(1 −z/c), so that

for γ

>γit follows that d

z/ dt

< 0, i.e. the deﬂected ﬂuid element

experiences a restoring force. The considered temperature distribution is

stable.

• When there is a value of γ = T

/c > γ

, a ﬂuid element deﬂected in the

positive z-direction experiences a positive force, i.e. the induced deﬂection

of the ﬂuid element is increased. This temperature distribution therefore is

unstable. The smallest ﬂuctuations of temperature and/or pressure in the

atmosphere will therefore “under these conditions” lead to the formation

of forces disturbing the considered temperature distribution.

17.2 Causes of Flow Instabilities 505

Summarizing, it can therefore be stated that for T = T

(1 −z/c)=(T

−

γz) the following holds:

γ<

: stable temperature distribution,

γ>

: unstable temperature distribution.

These insights into the physics of aerostatics have to be considered when

employing (17.10) for the pressure distribution in the atmosphere. It holds

only for γ<

The above derivations make it clear also that there are mechanisms present

in the atmosphere which often are not noticed and which are suited to

reduce temperature ﬁelds with strong gradients in the atmosphere. When

the local temperature gradient reaches γ-values that are larger than g/c

the higher temperatures lying below the considered point will rise upwards

when disturbances occur. An intermixing of the air layers results, such that

γ ≤ g/c

is achieved.

17.2.2 Gravitationally Caused Instabilities

In order to investigate the gravitation-dependent instability of an interface

between two ﬂuids, two inﬁnitely extended ﬂuids are considered which have a

common interface surface in the plane x

–x

(see Fig. 17.8). Here, the density

of the upper ﬂuid is ρ

and that of the lower ﬂuid is ρ

.Itismoreover

assumed that the surface tension in the interface layer is given by σ.Dueto

the assumption that the ﬂuid A expands in 0 ≤ x

< +∞ and the ﬂuid B

in −∞ <x

≤ 0, an instability problem results that is spatially dependent

only on x

As it is assumed that the considered ﬂuids in the upper and lower regions

are viscous media, the considerations that should be carried out, concerning

possible instabilities, should be based on the Navier–Stokes equations. When,

however, one starts from the assumption that the following holds:



g! 

, (17.24)

Fig. 17.8 Stratiﬁed ﬂuids and stability of their

interface

Fluid A with

density

Fluid B with

density

Plane between

two fluids

506 17 Unstable Flows

where ν/! is the characteristic “viscous velocity” and

√

g! is the character-

istic “gravitation velocity”, one can assume for the stability considerations

to be carried out here that gravitation eﬀects dominate when compared with

viscous inﬂuences. These facts allow the employment of the “viscosity-free”

form of the basic equations, in order to investigate the instability caused by

gravitation, i.e. the instability of the ﬂuids with the common interface shown

in Fig. 17.8. As the considerations to be carried out start from the assumption

that the ﬂuids are at rest before the action of a disturbance sets in, the ﬂuid

motion imposed by the disturbance will be irrotational from the beginning.

Therefore, it is recommended to treat the considered instability problem by

introducing the potentials φ

and φ

for ﬂuids A and B.

It is understandable that in the case of the inﬂuence of a disturbance on

the interface surface, i.e. on x

=0forallx

–x

values, one can expect for

→±∞that the velocities reach (U

)

=(U

)

= 0, so that one can set,

without limiting the universal validity of the considerations:

→ 0forx

→ +∞ and φ

→ 0forx

→−∞. (17.25)

As the solutions for φ

and φ

must, for viscous-free ﬂows, satisfy the Laplace

equation, the following ansatzes can be chosen:

,t)=C

exp(αt − kx

)S(x

), (17.26)

,t)=C

exp(αt + kx

)S(x

), (17.27)

where S(x

) has to satisfy the following partial diﬀerential equation:



∂

∂x

∂

∂x

+ k



S (x

)=0. (17.28)

On deﬁning with η the deﬂection of the interface surface, the following

kinematic relationship holds:

∂φ

∂x

∂φ

∂x

∂η

∂t

for x

= η. (17.29)

This relationship indicates that at the interface surface (U

)

has to be equal

to (U

)

and that the velocity is given by the deﬂection velocity of the inter-

face surface. Strictly there exists an equality for the normal components of

the velocities. For small deﬂections of the interface it can generally be as-

sumed, however, that the normal components of velocity are equal to the

vertical components. By introducing this equality into the considerations to

be carried out, a linearization of the problem is introduced, i.e. the subsequent

considerations can be assigned to the ﬁeld of the linear instability theory.

When considering the relations (17.26) and (17.27) for x

=0,onecan

write for η(x

,t)

η = C exp(αt)S(x

). (17.30)

17.2 Causes of Flow Instabilities 507

With (17.26), (17.27) and (17.30), one obtains from (17.29):

−kC

= kC

= Cα. (17.31)

For the pressure diﬀerence between ﬂuids A and B,oneobtains:

− P

= σ





= σ



∂

∂x

∂

∂x



. (17.32)

With (17.30) one obtains, with consideration of (17.28):

− P

= −σk

η. (17.33)

Statements on P

and P

can also be obtained via the Bernoulli equation:

= −

∂φ

∂t

− gη;

= −

∂φ

∂t

− gη. (17.34)

Hence one can derive

(−αC

− gC) − ρ

(−αC

− gC)=−σk

C. (17.35)

The elimination of C

, C

and C from (17.30) and (17.35) allows the

following derivation for α:

g (ρ

− ρ

) k

(ρ

+ ρ

)

−

σk

(ρ

+ ρ

)

, (17.36)

where α indicates the growth rate of a disturbance with time, (see (17.29)),

so that

g (ρ

− ρ

)

(ρ

+ ρ

)

−

σk

(ρ

+ ρ

)

≥ 1 (17.37)

or solved in terms of k

(ρ

− ρ

) >

2π

. (17.38)

This relationship expresses that in the case of inﬁnitely extended ﬂuids with

a common interface there always exists an ! which fulﬁlls the condition for

instability when ρ

>ρ

. Fluids with a common horizontal interface, where

the heavy ﬂuid is above, are inherently unstable. The ﬂuids tend to “turn

over,” i.e. the heavier ﬂuid tends to move to the lower location.

17.2.3 Instabilities in Annular Clearances Caused

by Rotation

In the preceding considerations in this chapter, instabilities of static ﬂuids

were considered see also refs. [17.2]. A ﬂow which proves unstable for cer-

tain parameter combinations was treated by Taylor [17.7]. He considered the

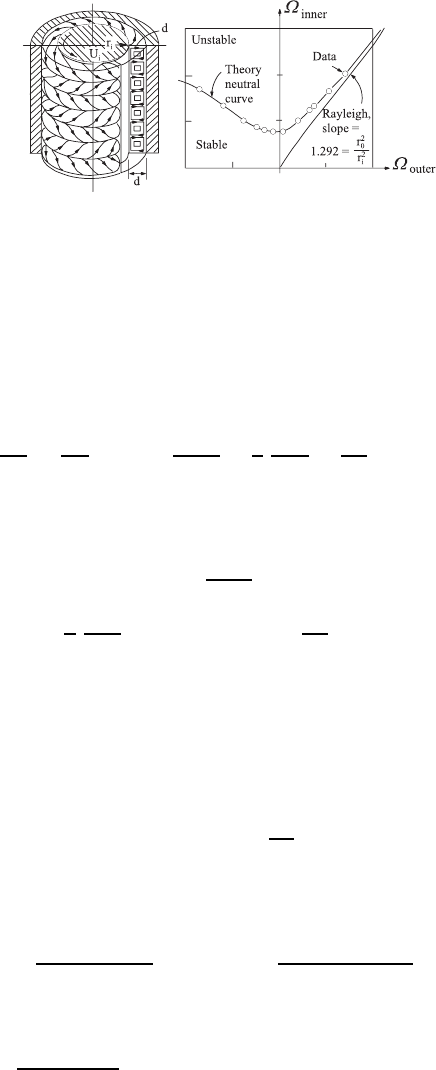
508 17 Unstable Flows

Fig. 17.9 Diagram of the vortex development for the Taylor annular-clearance ﬂow

and instability diagram

laminar ﬂow between two rotating cylinders, as sketched in Fig. 17.9. There,

the inner cylinder is assumed to rotate at a velocity (U

)

= R

and the

outercylinderat(U

)

= R

.ForU

=0andU

= 0, the following sys-

tem of equations results for the ﬂow in the annular clearance between the

two cylinders:

and

−

=0. (17.39)

The second diﬀerential equation for U

is of the Euler type and thus allows

particular solutions of the kind:

= C

;

dϕ

= C

k(k −1)r

k−2

= C

k−1

and

= C

k−2

(17.40)

This yields for k the general equation:

k(k − 1) + (k − 1) = (k +1)(k −1) = 0 (17.41)

and thus k

=1andk

= −1 are obtained. Therefore, the general solution

of the diﬀerential equation for the velocity U

reads:

= C

r +

. (17.42)

The integration constants C

and C

result from the boundary conditions

)=R

and U

)=R

, so that one obtains:

− ω

− R

and C

(ω

− ω

) R

− R

)

(17.43)

and thus for the velocity distribution U

(r):

(r)=

r (R

− R

)

− ω

+(ω

− ω

) R

. (17.44)

17.2 Causes of Flow Instabilities 509

The derivations carried out above show that the solution stated in (17.44)

for the ﬂow problem indicated in Fig. 17.9 fulﬁlls the Navier–Stokes equations

and the corresponding boundary conditions. The derivations carried out in

order to obtain the analytical solution leave, however, the question of the

stability of the solution unanswered, i.e. the extent to which disturbances

introduced into the ﬂow are attenuated or ampliﬁed still has to be resolved.

Taylor demonstrated that the question can be solved through purely analyti-

cal considerations. In accordance with Taylor’s considerations, we supplement

the above-indicated considerations by means of the following ansatzes for the

velocity components in the ϕ-, r-andz-directions:

= u



; U

= U

(r)+u



and U

= u



. (17.45)

On entering these velocity ansatzes into the basic equations and neglecting

the terms of second order, i.e. carrying out linear stability considerations, one

obtains the following equation system for the determination of the distur-

bances u



, u



and u



Continuity equation:

∂

∂r

(ru



∂

∂z

(ru



)=0. (17.46)

Momentum equations:

∂u



∂t

= −

∂p



∂r







+ ν



∂



∂z

∂



∂r

∂u



∂r

−





(17.47)

∂u



∂t

= −2C



+ ν

∂



∂z

∂



∂r

∂u



∂r

−



(17.48)

∂u



∂t

= −

∂p



∂z

+ ν



∂



∂z

∂



∂r

∂u



∂r



. (17.49)

Here, the boundary conditions u



= u



= u



=0forr = R

and r = R

hold. For their solution, the following ansatzes are now chosen:



= u

(r)cos(!z)exp(βt),u



= u

(r)cos(!z)exp(βt)and



= u

(r)sin(!z)exp(βt). (17.50)

Hence, the following equation system results for u

, u

and u

,whichall

depend only on the position coordinate r:



−

− !

2



=2C

, (17.51)

510 17 Unstable Flows



− !

2



= − 2





− ν



−

− !

2



, (17.52)

+ λu

=0, (17.53)

where the following holds for !



= !

. (17.54)

The system of equations for u

, u

and u

can be solved by ansatzes of

Fourier–Bessel series, where the development takes place in terms of the

Bessel function:

r)=α

r)+α

r) , (17.55)

where α

and α

are chosen such that the following holds:

)=z

)=0. (17.56)

Here

(r)=

∞



α=1

∞

r), (17.57)

where the coeﬃcients A

have to be determined by the following

relationships:

(r)z

r)dr with H

r)dr. (17.58)

For u

one obtains in accordance with (17.51):



−

− λ





=2C

∞



α=1

r) (17.59)

so that one obtains:

(r)=

∞



α=1

r) (17.60)

with the coeﬃcients B

being:

= −

ν (k

+ λ

2

)

. (17.61)

The boundary conditions u

)=u

) = 0 supply, however, u

(r)=0.

17.2 Causes of Flow Instabilities 511

To determine u

(r), the diﬀerential equation (17.53) is employed and a

known property of the Bessel function is implemented:

(kr)=−z

(kr) (17.62)

so that one obtains



− λ

2



=0. (17.63)

For this diﬀerential equation the following solution results:

(r)=z

(iλ



r)+constant. (17.64)

By employing the above solution, Taylor was able to demonstrate that in the

case of given values of ω

, ω

, R

and R

the quantities

λ and λ



(17.65)

are linked with one another.

Taylor carried out the above-indicated analysis in detail, assuming (R

−

) 

+ R

), i.e. his results hold for narrow annular clearances. His

results can be summarized as follows, in consideration of the stability diagram

in Fig. 17.10:

• When both cylinders, forming the annular clearance, rotate in the same

direction, the stability of the ﬂow is always guaranteed when R

holds (see Fig. 17.10).

• The elementary stability criterion given above is not applicable when the

rotating cylinders possess opposite directions of rotation.

• For

=1.292, the stability curve shown in Fig. 17.10 results. Here

the loss of stability is characterized by the so-called Taylor vortices that

form in the annular clearance. The directions of rotation of these vortices

alternate.

• With δ =(R

−R

)andU

= R

, the critical Taylor number Ta,where

the instability starts, can be stated as follows:

Ta=

≥ 41.3. (17.66)

The ﬂow forming in the annular clearance, due to the treated instability,

is laminar again.

• The energy which is introduced through the drive of the inner cylinder

drives the secondary vortices and, after the steady state of the ﬂow has

established itself, also the energy dissipation in the vortices.

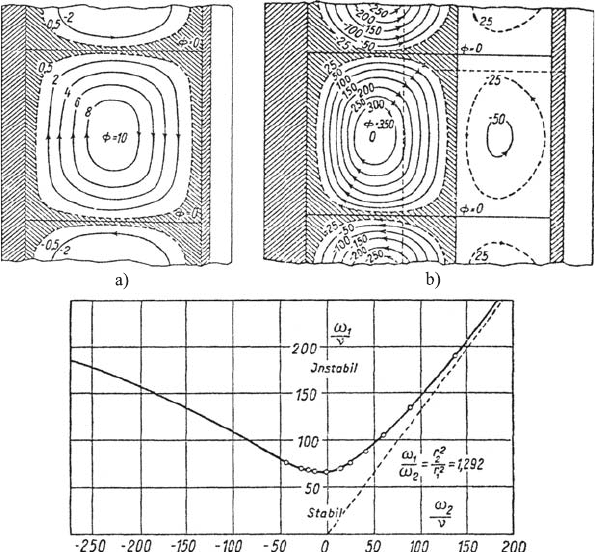
512 17 Unstable Flows

Fig. 17.10 (a) Vortex shapes between cylinders rotating in the same direction after

occurrence of the Taylor instability. (b) Vortex development with cylinders rotating

in the opposite direction after occurrence of the Taylor instability

It is interesting that in the cases of opposite directions of rotation of the two

cylinders, i.e. for ω

=0,thevalueforω

for which the Taylor instability

occurs increases again when departing from ω

= 0. It is further interesting

that the annular vortices change with the opposite mode of rotation. As

Fig. 17.10 shows, two vortex series form, one which is to be assigned to the

rotation of the inner cylinder and another which belongs to the rotation of

the outer cylinder.

17.3 Generalized Instability Considerations

(Orr–Sommerfeld Equation)

Section 17.2 showed to some extent how to proceed with considerations in the

framework of the linear instability theory. The approach presented there will

now be generalized for ﬂow computations for which the following disturbance

ansatzes hold, see also refs. [17.6]:

ˆu

= U

(y)+u



(x, y, t); ˆu

= u



(x, y, t); ˆu

=0, (17.67)