Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

15.2 Creeping Fluid Flows Between Two Plates 431

are carried out for viscous ﬂows of small Reynolds numbers, employing the

equations in (15.4). The considerations are carried out up to the computations

of forces, to make it clear how small Reynolds number ﬂows can be treated in

a complete way. The computations of forces require derivations of the pres-

sure distributions on the surface of bodies and also computations of the local

momentum losses of ﬂows at walls. The chosen examples are aimed to give a

suitable introduction to the treatments of ﬂows of small Reynolds numbers.

Solutions of other creeping ﬂow examples, going beyond the treatments in

this chapter, are easily possible and are often described extensively in books

on ﬂuid mechanics, see refs. [15.1] to [15.7]. Hence, no further considerations

of more complex ﬂows are needed here.

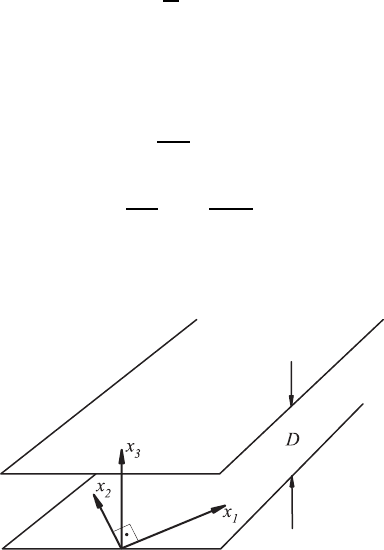
15.2 Creeping Fluid Flows Between Two Plates

In this section, the ﬂow of a viscous ﬂuid between two parallel plates is

considered, whose distance D can be regarded as being very small (Fig. 15.1).

When the area-averaged mean ﬂow velocity

U =

(15.5)

is also small, the conditions for the employment of the following diﬀerential

equations exist. When ρ = constant holds, then one can write

∂U

∂x

= 0 (15.6)

∂P

∂x

= µ

∂

∂x

, (15.7)

i.e. the Stokes diﬀerential equations can be employed to treat the ﬂow between

two parallel plates.

Fig. 15.1 The diagram shows the plates and the coordinate system for a ﬂow between

plates

432 15 Fluid Flows of Small Reynolds Numbers

This set of diﬀerential equations reads, written in full, for j =1, 2, 3:

∂U

∂x

∂U

∂x

∂U

= 0 (15.8)

j =1:

∂P

∂x

= µ



∂

∂x

∂

∂x

∂

∂x



(15.9)

j =2:

∂P

∂x

= µ



∂

∂x

∂

∂x

∂

∂x



(15.10)

j =3:

∂P

∂x

= µ



∂

∂x

∂

∂x

∂

∂x



. (15.11)

The above equations are valid within the limits −∞ <x

< +∞ and

0 ≤ x

≤ D. In addition, the ﬂow in the x

and x

directions is assumed

to be fully developed, i.e. ∂U

/∂x

=0and∂U

/∂x

= 0, so that one can

deduce from the continuity equation:

∂U

∂x

=0 ; U

= constant. (15.12)

Because U

=0forx

=0andx

= D, U

= 0 holds in the entire ﬂow region

between the two channel walls.

Due to the existence of fully developed ﬂow conditions in the x

and x

directions, the following diﬀerential equations hold:

∂P

∂x

= µ

∂

∂x

;

∂P

∂x

= µ

∂

∂x

;

∂P

∂x

=0. (15.13)

From these equations, one obtains for U



∂P

∂x



+ C

(15.14)

and for U



∂P

∂x



+ C

. (15.15)

The integration constants C

and C

can be determined from the boundary

conditions:

=0forx

=0andx

= D ; C

=0andC

= −

2µ

∂P

∂x

Thus one can derive for U

= −

2µ



∂P

∂x



(D − x

) (15.16)

15.3 Plane Lubrication Films 433

and likewise U

can be determined as:

= −

2µ



∂P

∂x



(D −x

). (15.17)

The equations for U

and U

show that the velocities diﬀer only due to the

pressure gradients imposed in the x

and x

directions.

With the aid of the above solutions for U

and U

, some further interesting

considerations can be carried out. The result is that the cross-sectional mean

velocities can be determined as follows, according to (15.5):

)=−

12µ



∂P

∂x



= −

12µ



∂P

∂x



, (15.18)

where

and

are the area-averaged velocities in the x

and x

directions.

On introducing the potential φ(x

), driving the mean ﬂow ﬁeld to an

extent that φ(x

)=−

12µ

P (x

) holds, then the following relationship

can be stated:

∂φ

∂x

and

∂φ

∂x

. (15.19)

These relationships between the components of the mean velocity ﬁeld and

the potential φ, express for the area-averaged ﬂuid velocity, the driving force

to be the diﬀerentials of φ. This essentially suggests that the ﬂow can be

regarded as having a block proﬁle and is formally running, like the vorticity-

free ﬂow of an ideal ﬂuid (potential ﬂow).

15.3 Plane Lubrication Films

Already daily experience shows that a ﬂuid ﬁlm between two plates has pos-

itive properties, as far as the sliding of one plate on another is concerned.

This provides insight into the ﬁlm action, suggesting that the forces acting

on two solid plates, that are exposed to a gliding process, can be reduced by

lubrication ﬁlms. One further notices that a ﬂuid ﬁlm placed between two

plates is able to absorb considerable forces. All these considerations make it

clear why ﬂuid ﬁlms can be used in so-called slide bearings in mechanical

systems, in order to make sliding and also rotating machine elements work

in practice. In order to understand the principal function of lubrication ﬁlms

and also their properties, the ﬂow in a very thin ﬁlm which develops between

two sliding plates is investigated. Such a ﬁlm which develops below a plate,

having a length l and leading to ﬁlm thicknesses h

and h

at the beginning

and end of the plate, respectively, is plotted in Fig. 15.2. Due to h

= h

an angle of inclination α develops by which the upper plate is inclined with

respect to the lower plate. Thus, the ﬁlm thickness h(x

) is determined by

the ﬁlm and its motion. Moreover, in the treatment of the ﬁlm motion, the

lower plate moves at a velocity U

relative to the upper plate.

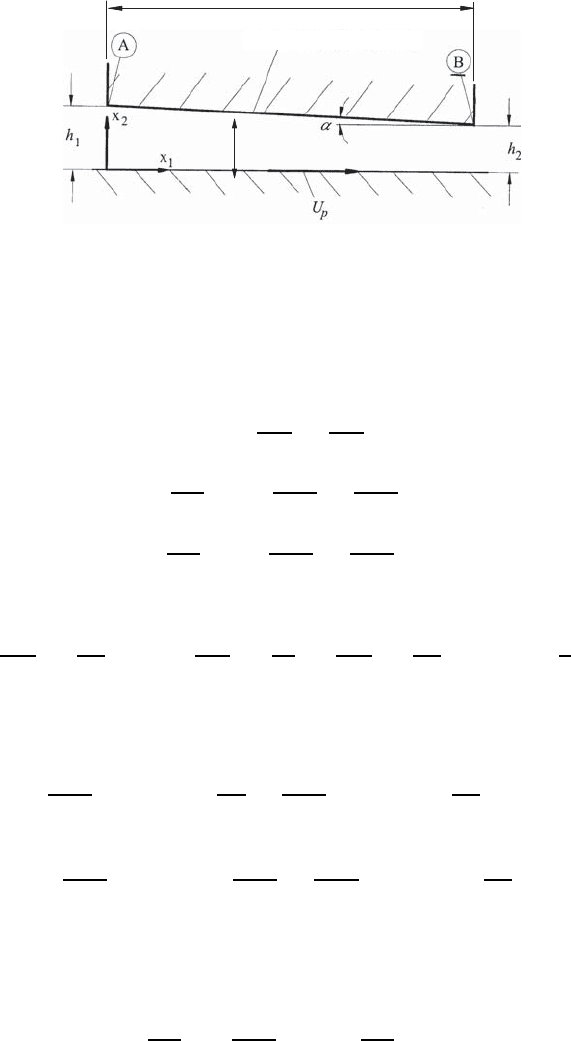
434 15 Fluid Flows of Small Reynolds Numbers

Lower plate (is moving)

Liquid film

)

Upper plate (is fixed)

Fig. 15.2 Considerations of the ﬂuid ﬂow between two plates (basic ﬂow of tripol-

ogy). U

= velocity of the moving lower plate; α = inclination angle between the

plates; R(x

) = variation of plate distance

For the ﬂow between the inclined plates, induced by the motion of the lower

plate in Fig. 15.2, (15.8)–(15.11) hold the Stokes’ equations in the following

form, because U

=0:

∂U

∂x

∂U

∂x

(15.20)

∂P

∂x

= µ



∂

∂x

∂

∂x



(15.21)

∂P

∂x

= µ



∂

∂x

∂

∂x



. (15.22)

Orders of magnitude considerations of the terms in (15.20) yield:



∂U

∂x



≈

and



∂U

∂x



∂U

∂x



≈ U





(15.23)

Because (h/l)  1, U

 U

(thin lubrication ﬁlm), the order of U

can be

computed. Similar considerations for the terms in (15.21) and (15.22) yield:

∂

∂x

=term1 ≈

;

∂

∂x

=term2 ≈

(15.24)

∂

∂x

=term3 ≈

;

∂

∂x

=term4 ≈

. (15.25)

Comparisons of terms 1–4 in (15.24) and (15.25) show that term 2 domi-

nates and that therefore the following simpliﬁed forms of (15.21) and (15.22)

describe, suﬃciently well, the ﬁlm ﬂow between two plates indicated in

Fig. 15.2:

∂P

∂x

= µ

∂

∂x

and

∂P

∂x

=0. (15.26)

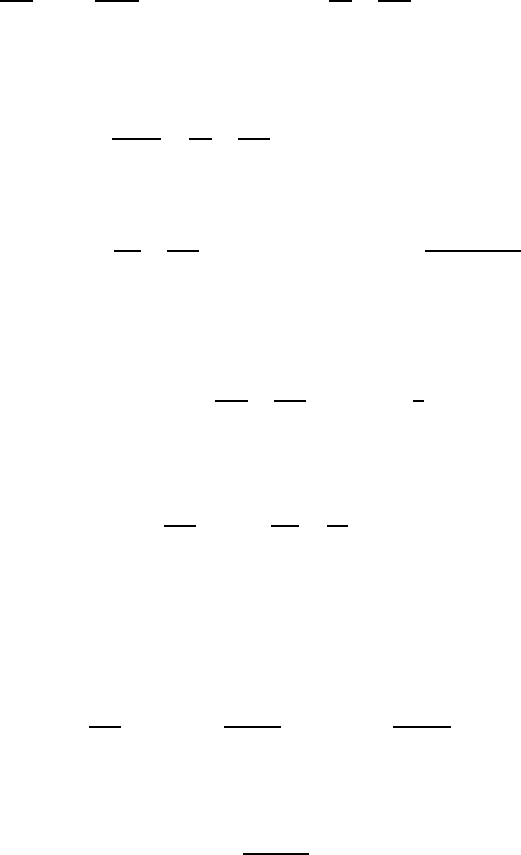
15.3 Plane Lubrication Films 435

For the induced ﬁlm ﬂow, the following boundary conditions hold:

=0 : U

, 0) = U

and x

= h(x

): U

,h)=0. (15.27)

Integrating ∂P/∂x

=0yieldsP = Π(x

), so that the diﬀerential equation

for the velocity ﬁeld reads



dΠ



= µ

∂

∂x

; U

2µ



dΠ



. (15.28)

With the boundary conditions in (15.27), the two integration constants in

(15.28) can be derived to read as follows:

= −

h(x

)

−

2µ



dΠ



h(x

)andC

= U

. (15.29)

Thus, the following equation for U

results:

−1

2µ



dΠ



[h (x

) − x

]+U



h (x

) − x

h (x

)



. (15.30)

The constant volume ﬂow rate of the ﬁlm ﬂow can be computed by

integration:

˙v (x

−1

12µ



dΠ



h(x

). (15.31)

Hence, the pressure gradient imposed by ˙v = constant is computed as follows:

dΠ

=6µ



−

2˙v



= f(x

). (15.32)

This relationship shows that the movement of the plates and the ﬂow with

avolumeﬂowrate ˙v within the ﬁlm lead to a pressure gradient dependent

on x

. In order to compute the pressure P (x

)=Π(x

), we carry out the

following integration, where P (x

=0)=P

= P

can be set:

P (x

)

dΠ

=6µ

)

− 12µ

˙v

)

. (15.33)

Simple geometric considerations yield:

h(x

)=h

−



− h



= h

− x

tan α. (15.34)

436 15 Fluid Flows of Small Reynolds Numbers

Hence, one can derive dh = −tan α dx

≈−α dx

, so that the following

result for the pressure distribution holds:

P (x

) − P

6µ





−



− ˙v



−



. (15.35)

As the ends of the slide bearing are exposed to the same ﬂuid space, P (x

= l)

= P

holds and one can derive from (15.35) the following:

˙v = U



+ h



. (15.36)

This relationship inserted in (15.32) yields for the pressure gradient in the

ﬂuid:

6µU

(h − h

)withh

+ h

)

. (15.37)

From this, it readily follows that:

> 0atthelocationh = h

;

< 0atthelocationh = h

= 0 at the location h = h

i.e. the pressure distribution in the liquid ﬁlm shows a maximum. For the

pressure distribution itself one can write:

P − P

σµU



− h)(h −h

)

+ h

)



. (15.38)

With the above relationships (15.36)–(15.38), the volume ﬂow rate and the

pressure distribution in the ﬁlm can be computed for the case that the relative

velocity of the moving plates is given and the entire bearing geometry can be

considered to be known. The employment of (15.38) yields P>P

, i.e.

the ﬁlm plotted in Fig. 15.2 produces an overpressure due to the indicated

relative movement of the plates. The ﬁlm is thus able to absorb forces that

act on the upper plate. A pressure maximum develops within the lubrication

ﬁlm at which the value of the pressure can be computed to be:

max

− P

= µl

. (15.39)

In this equation, the approximation (h

− h

) /h

≈ 1 has been introduced.

The resulting pressure force on the plate surfaces can be computed as follows:

P dx =

σµU



− 2

− h

)

+ h

)



. (15.40)

15.3 Plane Lubrication Films 437

The tangential force on the lower plate can be computed to yield:

)

low



∂U

∂y



y=0

dx =

2µU



− h

)

+ h

)

− 2ln





(15.41)

and for the upper plate:

)

= −



∂U

∂y



g=h

2µU



− h

)

+ h

)

− ln





. (15.42)

The tangential forces acting on the two surfaces of the plates are not equal

because the ﬂow between the plates is partly dragged along in the ﬁlm.

The ﬂow lines developing in the ﬁlm ﬂow are shown in Fig. 15.3, to-

gether with the plotted local velocity proﬁles. The proﬁles result from (15.30),

including (15.38) for the computations. The following was introduced:

ρU

µU

ρU





 1. (15.43)

The above considerations were carried out for plane ﬂows, as the intention

of the derivations was to give an introduction into the theory of tribological

ﬂows. Flows in slide bearings usually have to be treated as rotating cylinder

Guide

surface

Upper plate

Lower plate

Fig. 15.3 Flow lines and velocity proﬁle in a slide-bearing ﬂow

438 15 Fluid Flows of Small Reynolds Numbers

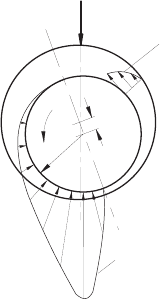
Fig. 15.4 Pressure distribution in rotating slide

bearings

Velocity

distribution

Force

Pressure

ﬂows with an eccentric bearing positioning of the inner cylinder, relative

to the outer one. This bearing case is plotted in Fig. 15.4, which shows the

developing pressure distribution due to rotation. It is characteristic for this

kind of ﬂow that the direction of the pressure maximum is not situated in the

direction of the load. Details of this ﬂow are treated in the following chapter.

They represent the basis for understanding the ﬂuid-mechanical functioning

of rotating slide bearings.

15.4 Theory of Lubrication in Roller Bearings

A roller bearing comprises a nonrotating bearing and a pivot rotating at

angular velocity ω. The practically employed double-cylinder arrangement is

shown in Fig. 15.5, with the following approximations being valid:

+ h ≈ R

+ e cos ϕ,

= R

+ e + δ,

h ≈ δ + e(1 + cos ϕ).

The solution of the equations for the ﬂuid motion, which is important for the

lubrication ﬂow in slide bearings, i.e. the rotating ﬂuid motion which develops

between pivot and bearing, probably represents the technically most impor-

tant application of Stokes’ equations. Due to the resultant ﬂuid movement

in a thin ﬁlm, well-known bearing friction laws result which diﬀer drastically

to those for dry friction laws. To demonstrate this, the motion of the inner

cylinder (pivot) having a radius r = R

is considered, which rotates at an-

gular velocity ω, while the outer cylinder (bearing), having the radius R

is at rest. The internal rotating cylinder thus has a circumferential velocity

U = R

ω. From the representation in Fig. 15.5, one can establish that the

position of the bearing can be given as r = R

+ h.Hereh = δ + e(1 + cos ϕ).

15.4 Theory of Lubrication in Roller Bearings 439

R =

Radius of pivot

= 0 : U = U

= h : U = 0

= h

r = R +

= 0

e cos

R =

Radius of bearing

Pivot

Bearing

Fig. 15.5 Bearing-pivot arrangement for considered roller bearing

These relationships hold with suﬃcient precision for the considerations car-

ried out. In this section, δ is the ﬁlm thickness of the lubrication ﬂuid existing

at ϕ = 180

◦

and e the eccentricity of the center point of the bearing with

regard to the position of the center point of the pivot.

On introducing into the considerations that the ﬁlm thickness δ is very

small with respect to the radius of the pivot, i.e. δ/R

 1 holds, then one can

show that ∂U

/∂r  1/r∂U

/∂ϕ holds. Order of magnitude considerations

of the remaining terms in the momentum equation (5.115) demonstrate that

the following diﬀerential equation can be employed for the treatment of ﬁlm

ﬂows in roller bearings:

∂P

∂ϕ

= µ

∂

∂r

. (15.44)

As the r values appearing in the ﬂow ﬁeld of the ﬁlm do not vary strongly,

the following approximation holds, because r ≈ R:

∂P

∂ϕ

= µ

∂

∂r

. (15.45)

Due to this simpliﬁcation, it is possible to treat the problem of roller bearings

in a way which comes close to that of the plane slide bearing.

Concerning the integration of the diﬀerential (15.45), one can proceed as

follows. The introduction of the variable ξ yields

r = R

+ ξ ; dr =dξ. (15.46)

Integration of (15.45) therefore yields:



dϕ



+ C

ξ + C

. (15.47)

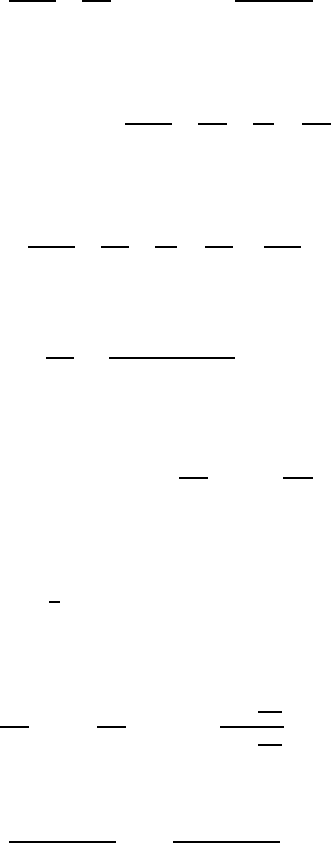
440 15 Fluid Flows of Small Reynolds Numbers

With the boundary conditions:

ξ =0 : U

= U and ξ = h : U

= 0 (15.48)

and C

can be determined, so that the following relationship holds:



∂P

∂ϕ



ξ (ξ − h)+

U(h − ξ)

. (15.49)

For the volume ﬂow rate, one can derive:

˙v =

R+h

dr =

dξ = −



∂P

∂ϕ



. (15.50)

Due to the introduction of a mean ﬁlm thickness h

with:

˙v = −



∂P

∂ϕ



(15.51)

and thus from (15.45), the following pressure gradient can be computed:

∂P

∂ϕ

6RµU(h − h

)

(15.52)

and by integration the pressure distribution results:

P (ϕ)=P(0) + 6R

µU

⎡

⎣

dϕ

− h

dϕ

⎤

⎦

. (15.53)

With h ≈ δ + e(1 + cos ϕ) from Fig. 15.5, the following results:

h(ϕ)=e



+1+cosϕ



= e (α +cosϕ) . (15.54)

Because P(2π)=P(0) = P

, according to (15.53) it must hold that:

2π

dϕ

= h

2π

dϕ

−→ h

2π

dϕ

2π

dϕ

. (15.55)

Considering:

2π

dϕ

(α +cosϕ)

dϕ

(α +cosϕ)

(15.56)