Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

15.7 The Slow Rotational Motion of a Cylinder 451

is compared with the pressure term:



∂P

∂r



θ=0

=3µ

∞

, (15.127)

i.e. put in relation to one another:





θ=0



∂P

∂r



θ=0

∞

2ν



1 −



1 −



. (15.128)

For large values of r, this relationship shows that the above solution should

be valid only when U

∞

r/2ν<1 holds, i.e. for large values of r the requested

condition for the validity of the solution is not fulﬁlled. As, however, for such

large values for r, the terms that have been employed above, for order of

magnitude considerations, become very small, it is justiﬁed to assume that

the velocity and pressure ﬁelds in the immediate proximity of the sphere are

not aﬀected by inﬂuences of the introduced assumption for the validity of

the obtained solution. In order to achieve the derived solution in a reliable

way, it had to be assumed, however, that (U

∞

R)/ν  1. On the basis of

such considerations, it can be assumed that the Stokes solution already does

not hold any longer for the ﬂow around a sphere for Re ≈ 1, i.e. when

Re =(U

∞

D/ν) ≈ 1. It is a solution for Re < 1.

15.7 The Slow Rotational Motion of a Cylinder

Analogous to the discussion of the slowly rotating ﬂow around a sphere in

Sect. 15.5, the rotating cylinder ﬂow will be discussed in this section. Here, the

ﬂow which occurs in the annular clearance between two concentric rotating

cylinders, with radii R

and R

, will be investigated. This ﬂow is described

by the equations that are stated below and which, assuming

∂U

∂ϕ

=0 and U

= U

(r) (15.129)

can be derived from the general basic equations of ﬂuid mechanics written in

cylindrical coordinates:

∂P

∂r

(15.130)

and





=0. (15.131)

These are the diﬀerential equations for the pressure P and the ﬂow velocity

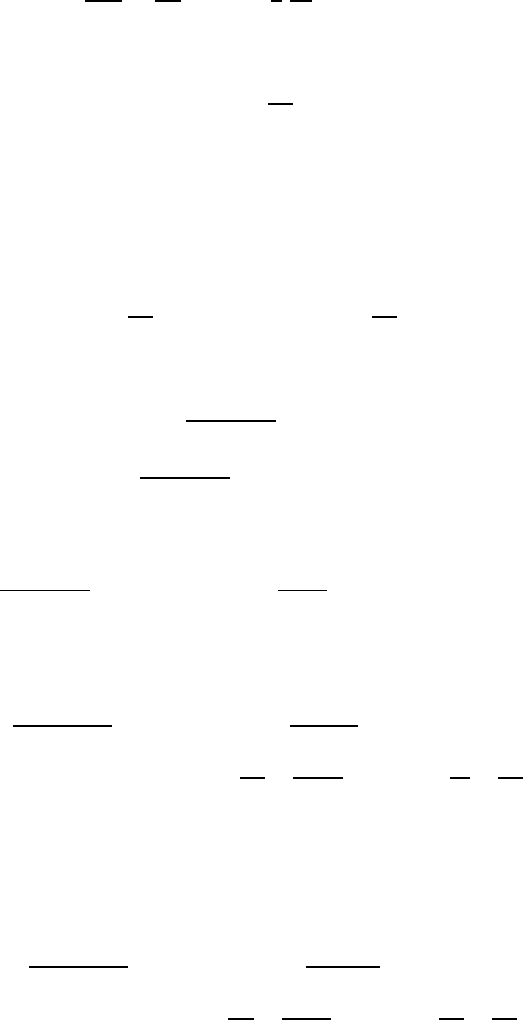
. From (15.131), one obtains by integration:

452 15 Fluid Flows of Small Reynolds Numbers

=2C

(rU

) . (15.132)

By further integration, one obtains:

= C

r +

(15.133)

with the integration constants C

and C

. These can be determined from the

boundary conditions:

r = R

; U

= ω

and r = R

; U

= ω

, (15.134)

i.e. the following equations hold for C

and C

= C

and ω

= C

(15.135)

and thus

= ω

− R

)

(ω

+ ω

) (15.136a)

− R

)

(ω

+ ω

) . (15.136b)

Inserting C

and C

in (15.133), one obtains:

− R

)



− ω

r −

(ω

− ω

)



. (15.137)

By means of (15.137), one obtains by integration from (15.130) for the

pressure distribution in the annular clearance:

P (r)=P

− R

)



− ω



− R



− 2R

(ω

− ω

)

− ω

−

(ω

− ω

)



−



(15.138)

The pressure at the internal cylinder wall was introduced in (15.138) with P

in order to determine the constant resulting from the integration of (15.130).

For the pressure distribution along the periphery of the external cylinder,

one can compute from (15.138)

P (R

)=P

− R

)



− ω



− R



− 2R

(ω

− ω

)

− ω

−

(ω

− ω

)



−



(15.139)

15.8 The Slow Translatory Motion of a Cylinder 453

For the molecular momentum transport, the following relationship holds:

rϕ

= −µ







. (15.140)

With the aid of the solution (15.137) for U

, one can compute

rϕ

−2µ

− R

)

(ω

− ω

) . (15.141)

The molecular-dependent momentum input into the internal cylinder amo-

unts to

rϕ

(r = R

−2µ

− R

)

(ω

− ω

) (15.142)

and for the external cylinder to

rϕ

(r = R

−2µ

− R

)

(ω

− ω

) . (15.143)

The circumferential forces acting on the cylinder can therefore be computed

as follows:

Fr(r = R

)=τ

rϕ

(r = R

)2πR

L = F

(r = R

)=τ

rϕ

(r = R

)2πR

L = F

(15.144)

From the relationships for the forces, one can see that the resulting circum-

ferential forces are directly proportional to the viscosity, a fact which is used

in the production of viscosimeters to measure the viscosities of ﬂuids.

15.8 The Slow Translatory Motion of a Cylinder

The considerations carried out at the end of Sect. 15.6 show that perform-

ing ﬂuid-ﬂow computations with induced simpliﬁcations into basic equations,

can lead to solutions for which, in some subdomains of the ﬂow ﬁeld, the as-

sumptions made for the simpliﬁcations are no longer valid. This fact has

resulted in some regions for the Stokes solution of the ﬂow around a sphere,

e.g. in regions where U

∞

r/ν ≥ 1. In these regions far away from the sphere,

the Reynolds number of the ﬂow becomes too large. There, the acceleration

terms, neglected in the Stokes solution ansatz, prove to be no longer small

in comparison with the considered pressure terms. Basically, unsatisfactory

argumentations had to be used to justify the validity of the obtained solution.

Strictly, only experimental investigations for determining the drag force on

the sphere could conﬁrm the correctness of the argumentation.

The problematic nature shown for the ﬂow around a sphere becomes even

clearer when one looks at the corresponding cylindrical problem, i.e. the

two-dimensional ﬂow around a cylinder. It shows indeed that for the plane

ﬂow around a cylinder of a viscous ﬂuid no solution at all can be found by

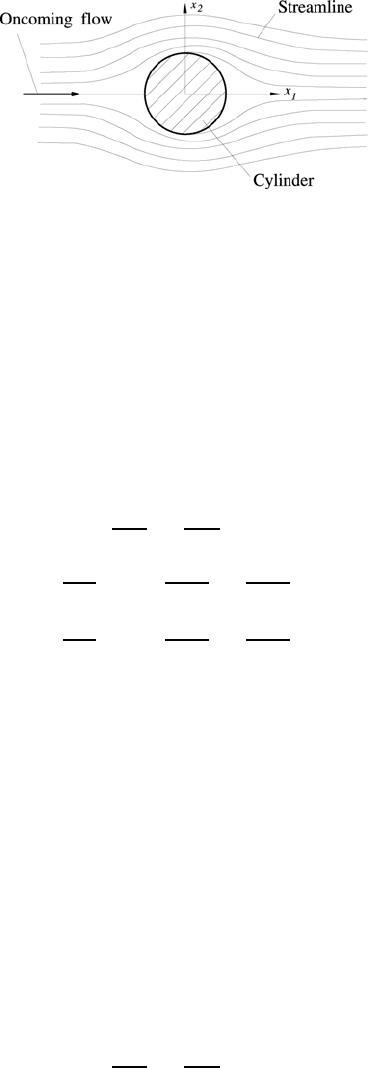
454 15 Fluid Flows of Small Reynolds Numbers

Fig. 15.9 Diagram of the ﬂow around a cylinder

employing the diﬀerential equations (15.4) or (15.6) and (15.7) or (15.8)–

(15.11). It is thus very problematic not to employ the complete set of basic

equations when solving ﬂow problems, but to use reduced sets of diﬀerential

equations. The latter approach is, however, often necessary for the reason

that analytical solutions for the complete set of the basic equations are not

available.

For the ﬂow around a cylinder, shown in Fig. 15.9, the following diﬀerential

equations hold, when assuming a ﬂow possessing a small Reynolds number,

i.e. to postulate the validity of the Stokes equations:

∂U

∂x

∂U

∂x

= 0 (15.145)

∂P

∂x

= µ



∂

∂x

∂

∂x



(15.146)

∂P

∂x

= µ



∂

∂x

∂

∂x



(15.147)

with the boundary conditions:

= U

=0 for r = R (15.148)

= U

∞

=0 for r →∞. (15.149)

The analytical solution that can now be determined for the above diﬀeren-

tial equations, proves to be of a form such that the boundary conditions

introduced for r = R and r →∞lead to two solutions that contradict one

another. Thus, it is consequently not possible to solve the simpliﬁed ﬂow

equations (15.145)–(15.147), in which the acceleration terms were neglected,

for the boundary conditions stated in (15.148) and (15.149). This insight

into the problem suggests leaving the acceleration terms in the basic equa-

tions. For the plane problem of the ﬂow around a cylinder, for ρ = constant

and stationary ﬂow conditions, one obtains the following set of diﬀerential

equations:

∂U

∂x

∂U

∂x

= 0 (15.150)

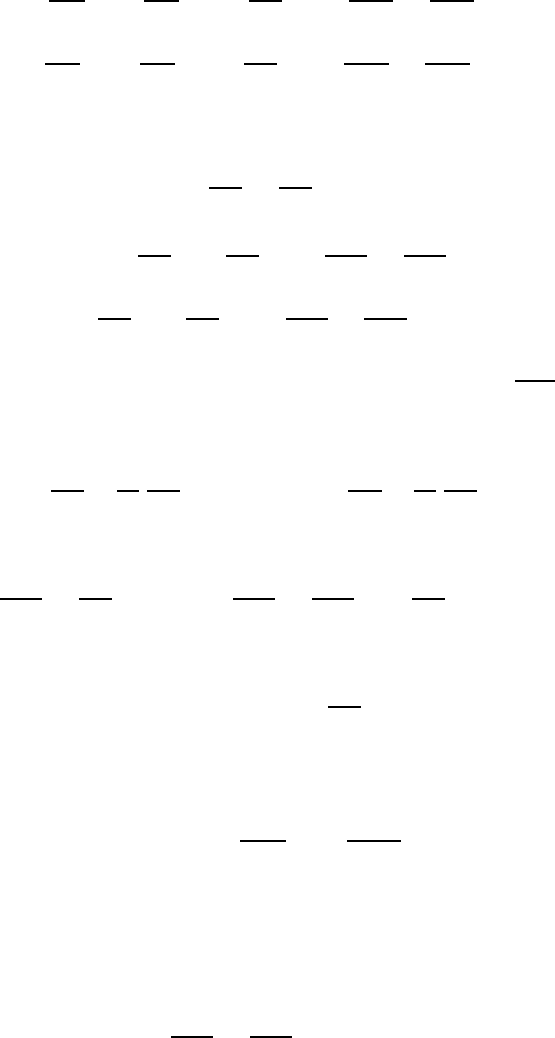
15.8 The Slow Translatory Motion of a Cylinder 455



∂U

∂x

+ U

∂U

∂x



= −

∂P

∂x

+ µ



∂

∂x

∂

∂x



(15.151)



∂U

∂x

+ U

∂U

∂x



= −

∂P

∂x

+ µ



∂

∂x

∂

∂x



. (15.152)

With U

= U

∞

+ u

and U

= u

, the following set of equations results,

assuming U

∞

 u

to yield the generalized Stokes equations:

∂u

∂x

∂u

∂x

= 0 (15.153)

ρU

∞

∂u

∂x

= −

∂P

∂x

+ µ



∂

∂x

∂

∂x



(15.154)

ρU

∞

∂u

∂x

= −

∂P

∂x

+ µ



∂

∂x

∂

∂x



. (15.155)

Introducing the potential function φ(x

), one obtains with

∂

∂x

=0,

according to a solution path proposed by Lamb (1911), the following ansatz

for u

and u

∂φ

∂x

∂χ

∂x

− χ and u

∂φ

∂x

∂χ

∂x

, (15.156)

where the quantities φ and χ fulﬁl the following diﬀerential equations:

∂

∂x

∂φ

∂x

=0 and

∂

∂x

∂

∂x

− 2k

∂χ

∂x

=0. (15.157)

Equations (15.153)–(15.155) are all fulﬁlled, when one inserts for the pressure:

P = P

∞

− ρU

∞

∂φ

∂x

. (15.158)

For φ(x

), the following ansatz can be found, in order to fulﬁl the

diﬀerential equation (15.157):

φ = A

ln r + A

∂ ln r

∂x

+ A

∂

ln r

∂x

+ ··· . (15.159)

For χ(x

), one introduces:

χ = ψ exp(kx

) (15.160)

so that for the determination of ψ the following diﬀerential equation results:

∂

∂x

∂

∂x

− k

ψ = 0 (15.161)

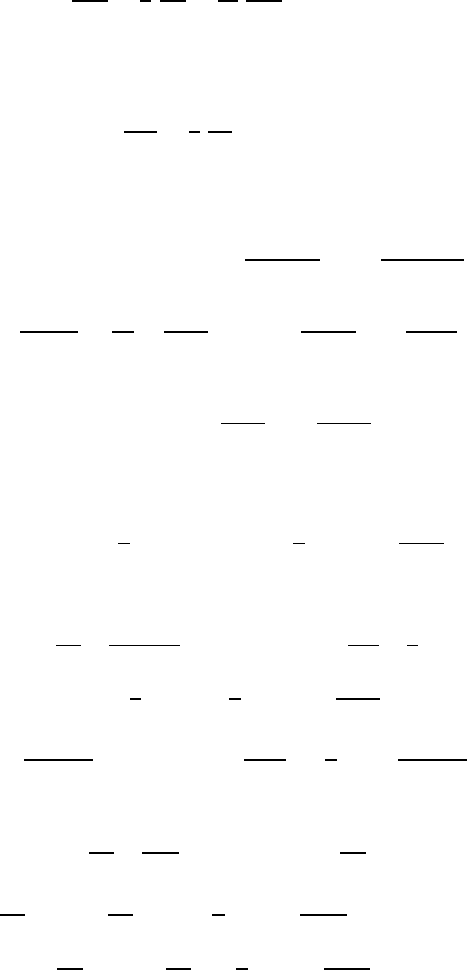
456 15 Fluid Flows of Small Reynolds Numbers

or in cylindrical coordinates:

∂

∂r

∂ψ

∂r

∂

∂ϕ

− k

ψ =0. (15.162)

On now looking for the solution of this equation, which depends on r,one

obtains the following ordinary diﬀerential equation:

dφ

− k

φ =0. (15.163)

This diﬀerential equation is determined by the Bessel function K

(kr)and

its derivatives, so that the following ansatz seems reasonable:

χ = −U

∞

+exp(kx)



(kr)+B

∂K

(kr)

∂x

+ B

∂

(kr)

∂x

+ ···



(15.164)

Because

∂(ln r)

∂x

cos ϕ

and

∂

ln r

∂x

= −

cos 2θ

(15.165)

it can be derived that:

φ = A

ln r + A

cos ϕ

− A

cos 2ϕ

. (15.166)

For the function χ one can write, on introducing the Mascheroni constant,

γ = 1.7811 or ln γ = 0.57722:

χ = −U

∞

− B







+ kr cos ϕ ln





− B

cos ϕ

(15.167)

so that for the velocity ﬁeld in cylindrical coordinates one can write:

(r, ϕ)=

−

cos ϕ

+ U

∞

cos ϕ − B



2kr

cos ϕ (15.168)

−

cos ϕ ln





+ B

cos ϕ

2kr

(r, ϕ)=−

sin ϕ

− U

∞

sin ϕ − B

sin ϕ





sin ϕ

2kr

. (15.169)

Including the boundary conditions for r = R,oneobtains:

−

2kR

=0 ; A

(15.170)

+ U

∞

−



1 − ln





2kR

= 0 (15.171)

−

− U

∞

−







2kR

=0. (15.172)

Thus, one obtains for the integration constants:

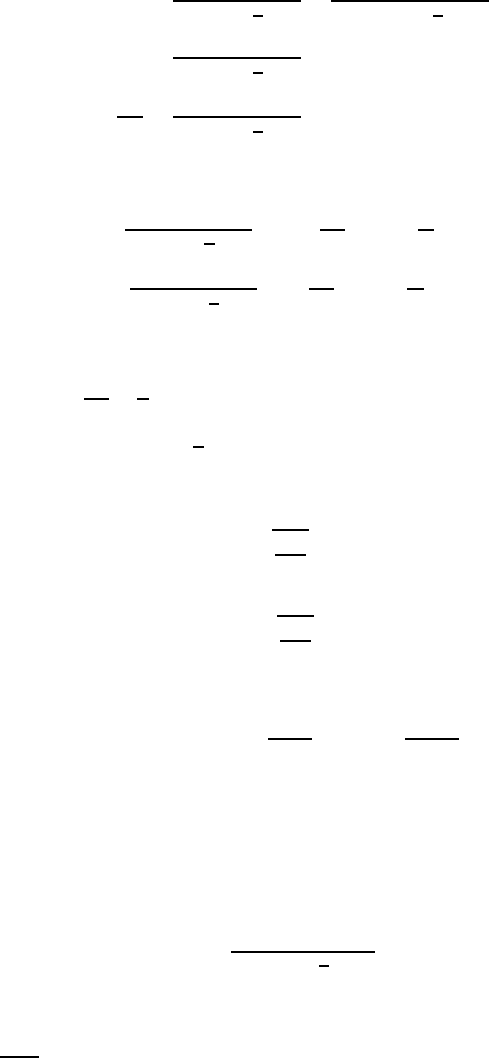
15.8 The Slow Translatory Motion of a Cylinder 457

4ν

1 − 2ln

∞

1 − 2ln

(15.173)

∞

1 − 2ln

(15.174)

−

−U

∞

1 − 2ln

. (15.175)

This yields for the velocity components in proximity of the cylinder:

(r, ϕ)=

∞

cos ϕ

1 − 2ln



−1+

+2ln







(15.176)

(r, ϕ)=

−U

∞

sin ϕ

1 − 2ln



1 −

+2ln







. (15.177)

For large distances the following equations hold for the velocity components:

(r, ϕ)=

exp (kr cos ϕ)[K



(kr) − cos ϕK

(kr)] (15.178)

(r, ϕ)=

exp (kr cos ϕ) K

(kr)sinϕ, (15.179)

where for large arguments (kr) the following asymptotic relationships hold:

(kr) ≈

2kr

exp(−kr) (15.180)

and



(kr) ≈−

2kr

exp(−kr). (15.181)

The pressure can be computed as:

P = P

∞

− ρU

∞

cos ϕ

+ ρU

∞

cos 2ϕ

. (15.182)

For the drag force, the following equation results:

=2πρU

∞

. (15.183)

When A

is inserted, the Lamb equation for the drag force per unit length

of a cylinder results:

8πµU

∞

1 − 2ln

. (15.184)

Although the acceleration terms are taken into consideration, the above

relation for F

, i.e. (15.184), can only be employed for small values for

Re =

∞

< 1.

458 15 Fluid Flows of Small Reynolds Numbers

Fig. 15.10 Stream lines for ﬂows around a cylinder at diﬀerent Reynolds numbers

Fig. 15.11 Drag coeﬃcients for the ﬂows around cylinders

If one does not want to have the above limitations of the derived solution

of the considered ﬂow problem, i.e. if one seeks a solution without any re-

strictions for the ﬂow around a cylinder, one has to solve the complete set of

equations numerically. Such solutions are nowadays possible for Re ≤ 10.000

by direct solutions of the continuity and Re−equations. They lead to the

results shown in Fig. 15.10 for the stream lines of the ﬂows. In Fig. 15.11, so-

lutions for the drag coeﬃcient of ﬂuid ﬂows for small Reynolds numbers are

shown. Fluid ﬂows information for small Re−number ﬂows around spheres

are provided in Fig. 15.12.

15.9 Diﬀusion and Convection Inﬂuences on Flow Fields 459

Fig. 15.12 Recirculating ﬂow regions behind spheres, from the book of Van Dyke

[15.8]

15.9 Diﬀusion and Convection Inﬂuences on Flow Fields

In paragraphs 3 and 5 the analogy of heat conduction and molecular momen-

tum transport is underlined and, in order to emphasize the signiﬁcance of

this analogy, the general form of the momentum equations was transformed

into the transport equation for vorticity (see Chap. 5):



∂ω

∂t

+ U

∂ω

∂x



= ρω

∂U

∂x

+ µ

∂

∂x

. (15.185)

For the two-dimensional ﬂow around a cylinder, ω

= ω is the only compo-

nent which is unequal to zero, and this fact allows one to write the vorticity

equation as a scalar equation. Because ρω

∂U

∂x

= 0, this equation reads:



∂ω

∂t

+ U

∂ω

∂x



= µ

∂

∂x

. (15.186)

On comparing this equation with the heat or mass transport equations for

convective and diﬀusive transport:

ρc



∂T

∂t

+ U

∂T

∂x



= λ

∂

∂x

and ρ



∂c

∂t

+ U

∂c

∂x



∂

∂x

. (15.187)

one sees that one can understand the inﬂuence of walls on ﬂows in such a way,

that at the boundary of the body the vorticity ω is produced. The vorticity

is then transported from the body to the ﬂuid, by molecular diﬀusion, into

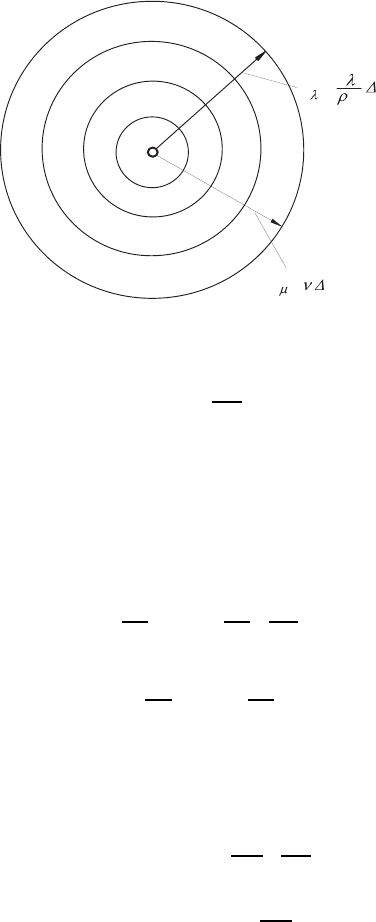
the moving ﬂuid, see Fig. 15.13.

In order to understand now the interaction between convection and diﬀu-

sion, it is thus possible to consider the diﬀusive and convective heat transport,

and to transfer the insight gained in this way to the vorticity and its transport

in the ﬂow ﬁeld.

On considering a heated cylinder with a small diameter when a sudden

temperature increase takes place, it can be seen that in a time ∆t,aheat

front dissipates as follows, due to heat conduction:

460 15 Fluid Flows of Small Reynolds Numbers

R ~

Expansion

heat

Expansion

vorticity

Fig. 15.13 Spreading of head and momentum by diﬀusion only

=const

ρc

∆t, (15.188)

where R

is a measure of the radial propagation, the heat has moved in the

time ∆t. For the vorticity one can write in an analogous way

=constν ∆t. (15.189)

For the diﬀusion velocity one thus obtains:

∆

=const



ρc



(15.190)

∆

=const

ν. (15.191)

When a ﬂuid now moves convectively at a small ﬂow velocity U

= U

∞

the state illustrated in Fig. 15.14 results, which is characterized by the fact

that a point can be found on the x

axis, at which the dissipation velocity is

= U

∞

,sothat

)

= R

=const

∞



ρc



(15.192)

)

= R

=const

∞

. (15.193)

With this it can be understood that in the presence of an inﬂow the inﬂuence

of the cylinder on the temperature or velocity ﬁeld can have an eﬀect in a

limited area only, as Fig. 15.14 shows. To the right of point (x

)

, there is no

information at all about the body lying in Fig. 15.14. The insights explained

in Fig. 15.14 are important when one has to ﬁnd in the inﬂow domain of a