Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

15.4 Theory of Lubrication in Roller Bearings 441

and because:

dϕ

(α +cosϕ)

√

− 1

arctan

α − 1

α +1

tan

(15.57)

one obtains for J

(ϕ = π), J

(ϕ = π), etc.

2π



(α

− 1)

; J

= −

dα

2πα



(α

− 1)

; J

= −

dα

2α



(α

− 1)

(15.58)

Thus, from (15.51) one can compute

= e

2eα

− 1

(2α

+1)

with α =





. (15.59)

For the pressure distribution between pivot and bearing (Fig. 15.6), one can

compute

P (ϕ) − P

=6R

µU

⎡

⎣

dϕ

(α +cosϕ)

2eα

− 1

(2α

+1)

dϕ

(α +cosϕ)

⎤

⎦

(15.60)

From (15.52), one can see that

∂P

∂ϕ

=0forh = h

On deﬁning with the angle ϕ

the angular position, where the pressure

shows an extremum, one obtains from (15.54)

e (α +cosϕ

2eα

− 1

(2α

+1)

(15.61)

cos ϕ

= −

3α

2α

. (15.62)

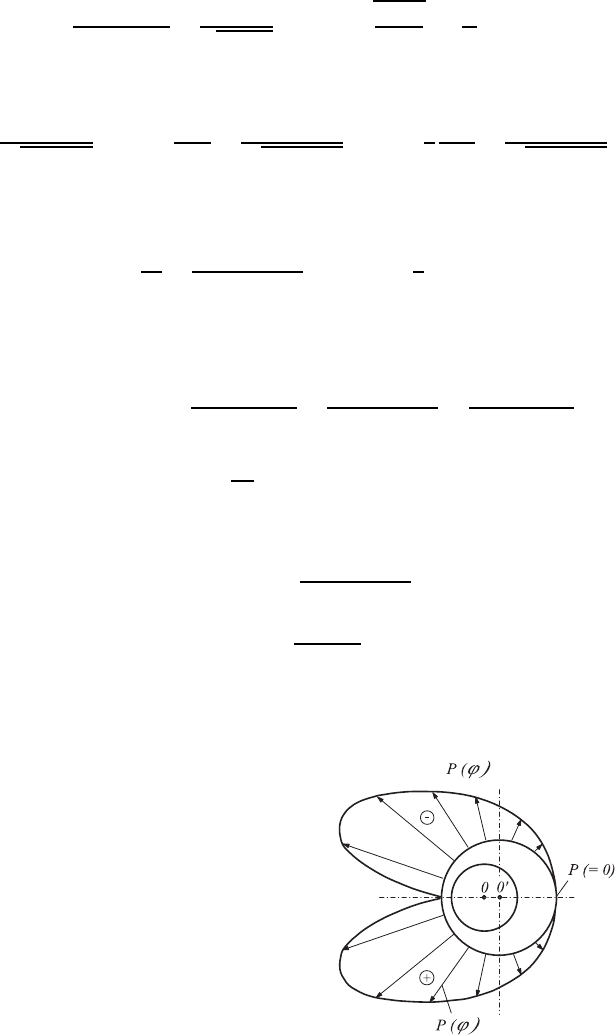
With this relationship, it has been shown that the points of highest and

lowest pressure are positioned on that half of the pivot circumference that

comprises the narrowest ﬁlm.

Fig. 15.6 Distribution of the normal pressure

on the pivot of a roller bearing

442 15 Fluid Flows of Small Reynolds Numbers

The derived pressure distribution can be used to compute the share of the

pivot force resulting from the pressure actions only.

By integration, one obtains:

12πµR

(2α

+1)

√

− 1

. (15.63)

For determining the friction force, the momentum loss due to the motion of

the pivot can be stated as follows:

rϕ

= −µ



∂U

∂ϕ

∂U

∂r

−



(15.64)

and because U

= U and U

= 0 hold on the pivot surface r = R

,onecan

deduce for τ

rϕ

= −µ



∂U

∂ξ



ξ=0

−

∂P

∂ϕ

Uµ

. (15.65)

With (∂P/∂ϕ)=6RµU(h − h

)/h

and h

inserted from (15.60), the

following results for the pressure gradient:

∂P

∂ϕ

µU



(α +cosϕ)

−

2α(α

− 1)

(2α

+1)

(α +cosϕ)



(15.66)

and for τ

rϕ

= µ

U(4h − 3h

)

2µU



(α +cosϕ)

−

3α(α

− 1)

(2α

+1)

(α +cosϕ)



so that the torque can be computed as:

M =

2π

rϕ

dϕ =

2µUR

2π(α

+2)

(2α

+1)

√

− 1

. (15.67)

In practice, the above equations can be employed as follows:

• When K

,µ,U,R,e,δ are known, the extremity of the pivot position and

also α can be determined by means of (15.63).

With (15.67), a friction factor can be introduced as

f =

3α

. (15.68)

As δ ≈ e holds in practice, one can deduce

≈

; M ≈ f

. (15.69)

15.5 The Slow Rotation of a Sphere 443

With this value, friction moments can be computed with suﬃcient accuracy

for application in practice. For large values of α, the following holds for M:

M =

2πµUR

. (15.70)

The above derivations have shown, in an exemplary way, that with the aid

of Stokes’ equations it is possible to treat technically relevant ﬂuid ﬂows in

such a manner that not only technically interesting insights result from the

derivations, but also quantitative results can be obtained.

15.5 The Slow Rotation of a Sphere

Considering the ﬂow in a viscous ﬂuid, which is caused by the slow rotation

of a small sphere, its Reynolds number can be determined as follows:

Re =

ωR

, (15.71)

where ω is the angular velocity of the rotation. Applying to the equations of

motion in spherical coordinates the conditions that exist due to the motion

of a sphere, as plotted in Fig. 15.7, then for

= U

(r, θ) (15.72)

the following diﬀerential equation holds, which represents an equation of

second order. This diﬀerential equation can be derived from the general

equations of motion in spherical coordinates:

Fig. 15.7 Flow in a viscous ﬂuid due to the

rotation of a sphere around the x

axis

444 15 Fluid Flows of Small Reynolds Numbers



∂

∂r



∂U

∂r



sin θ

∂

∂θ



sin θ

∂U

∂θ



sin

∂

∂φ

−

sin

sin θ

∂U

∂φ

2cosθ

sin

∂U

∂φ



. (15.73)

Because of the chosen rotational symmetry, the following terms are zero:

sin θ

∂U

∂φ

2cosθ

sin

∂U

∂φ

, and

sin

∂

∂φ

. (15.74)

Thus, (15.73) obtains the following form:

∂

∂r

∂U

∂r

∂

∂θ

cot θ

∂U

∂θ

−

sin

. (15.75)

As boundary condition one can write U

(R, θ)=Rω sin θ.

The aim of the solution of the ﬂow problem is to ﬁnd a function U

(r, θ),

which fulﬁls the diﬀerential equation (15.75), and at the same time is able to

fulﬁl the stated boundary conditions. Such a function proves to be:

= A(r)sinθ. (15.76)

Insertion of (15.76) into (15.75) yields:

sin θ +

sin θ −

sin θ +

cos

sin θ

−

sin θ

= 0 (15.77)

and as the diﬀerential equation for A(r)tobesolved:

−

=0. (15.78)

Integration of this diﬀerential equation yields

A(r)=C

r +

. (15.79)

Because U

(r →∞,θ) = 0, it follows that C

=0.

From U

(R, θ)=Rω sin θ =

sin θ it follows that C

= ωR

, and hence

one obtains as a solution for the velocity ﬁeld of the ﬂuid of the rotating

sphere:

ωR

sin θ. (15.80)

In order to maintain this ﬂow, imposed on the ﬂuid by the rotating sphere, a

moment has to be imposed continuously, which can be computed as derived

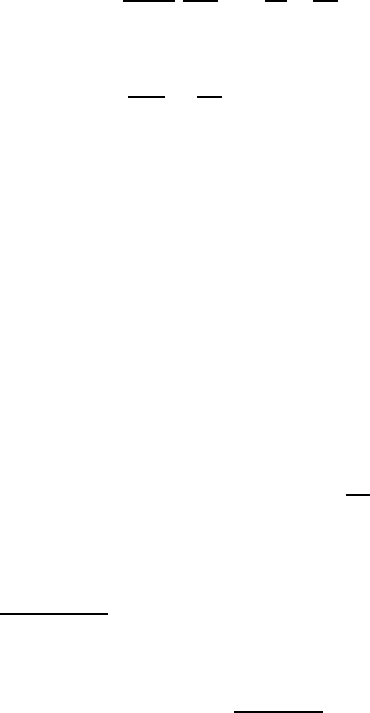
15.6 The Slow Translatory Motion of a Sphere 445

below. From

r,φ

= −µ



r sin θ

∂U

∂φ

+ r

∂

∂r





(15.81)

it follows for the momentum release to the ﬂuid by the rotating sphere:

R,φ

= −µ



∂U

∂r

−



r=R

=3µω sin θ (15.82)

and for this the moment can be computed to be:

M = −

(3µω sin θ)(R sin θ)

2πR

sin θ

dθ (15.83)

M = −6πµωR

sin

θ dθ =8µπR

ω. (15.84)

Analogous to the above solution concerning the problem of the ﬂuid motion

around a rotating sphere, the creeping ﬂuid motion between two concentri-

cally positioned rotating spheres, with radii R

and R

and angular velocities

and ω

, can be treated. The rotation is to take place again around the x

axis shown in Fig. 15.7. One obtains once more:

= A(r)sinθ with A(r)=C

r +

. (15.85)

With the boundary conditions A(R

)=ω

and A(R

)=ω

,one

obtains as a solution for the induced velocity ﬁeld:

(r, θ)=

sin θ

− R

)

− R

− ω

− R

(15.86)

and for the torque one can compute:

M = −8πµ(ω

− ω

)

− R

)

. (15.87)

As far as the above solution is concerned, it was assumed that the eventually

occurring disturbances of the ﬂow are attenuated by viscous eﬀects, i.e. that

the computed solution is thus stable. On the basis of the treatment of creeping

ﬂows, i.e. smallest Reynolds numbers, this assumption is justiﬁed, so that the

above analytically obtained results are very well obtained in experiments also.

15.6 The Slow Translatory Motion of a Sphere

The ﬂow around a sphere is considered in this section, as induced by the

straight and uniform motion of the considered sphere in a viscous ﬂuid. As

far as the equations to be solved are concerned, the problem is equivalent

446 15 Fluid Flows of Small Reynolds Numbers

to the ﬂow around a stationary sphere in a viscous ﬂuid. The speciﬁc ﬂuid

motion is characterized by a sphere of radius R, the ﬂuid velocity U

∞

,the

density ρ and the dynamic viscosity µ. From these, the Reynolds number of

the ﬂow problem is computed with ν = µ/ρ:

Re =

∞

< 1. (15.88)

Stokes (1851) was the ﬁrst to solve the problem of the translatory motion

of a sphere in a viscous ﬂuid by considering only the pressure and viscosity

terms in the Navier–Stokes equations and neglecting all other terms in the

equations of motion. The same procedure is shown below. In this context,

a stationary sphere, located in the center of a Cartesian coordinate system,

is assumed in the subsequent considerations. For this ﬂow case the following

boundary conditions hold:

= U

=0 for r = R

with r =



+ x

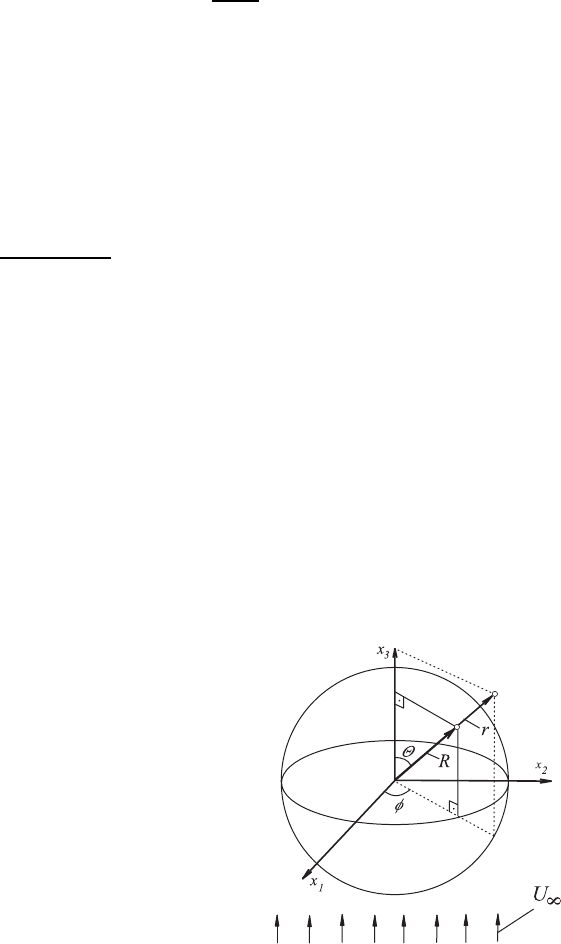
, as shown in Fig. 15.8. This ﬁgure shows the sphere

whose center is at the origin of a Cartesian coordinate system. Relative to

this system, the coordinates of the spheres r, φ, θ are also indicated, which are

subsequently employed for the treatment of the ﬂow around the considered

sphere. The surface of the sphere is located at r = R. Because of this assump-

tion of the location of the ﬂow boundary, it is advantageous to take the basic

equations of ﬂuid mechanics, for the solution of the ﬂow around a sphere, in

spherical coordinates. In this way, the boundary conditions, imposed by the

presence of the sphere, can be included much more easily into the solution

of the ﬂow problem, as if the treatment of the ﬂow in Cartesian coordinates

was sought.

The following considerations are based on the diagram in Fig. 15.8. At

inﬁnity, i.e. for r →±∞, the following values for the velocity components

will establish themselves:

Fig. 15.8 Flow around a sphere with

Cartesian and spherical coordinates

15.6 The Slow Translatory Motion of a Sphere 447

=0,U

= U

∞

for r →∞. (15.89)

As already mentioned, for the solution of the basic equations for ﬂows around

spheres, it seems obvious to employ the equations in spherical coordinates, in

order to be able to include the boundary conditions easily into the solution.

When considering the relevant terms for small Reynolds numbers, one ob-

tains the equations below. They can be derived from the general form of the

basic equations of ﬂuid mechanics, using spherical coordinates. The resulting

equationsreadasfollowsforStokesﬂows:

∂U

∂r

∂U

∂θ

cos θ

= 0 (15.90)

∂P

∂r

= µ



∂

∂r

∂

∂θ

∂U

∂r

cot θ

∂U

∂θ

−

∂U

∂θ

−

2cotθ



(15.91)

∂P

∂θ

= µ



∂

∂r

∂

∂θ

∂U

∂r

cot θ

∂U

∂θ

∂U

∂θ

−

sin



. (15.92)

In spherical coordinates, the boundary conditions can be stated as follows:

r = R : U

(R, θ)=0 and U

(R, θ) = 0 (15.93)

r →∞: U

→ U

∞

cos θ and U

→−U

∞

sin θ. (15.94)

Again, the boundary conditions suggest solving the above diﬀerential

equations with the following solution ansatzes for U

and U

(r, θ)=B(r)cosθU

(r, θ)=−A(r)sinθ (15.95)

and for the pressure:

P (r, θ)=µC(r)cosθ. (15.96)

On inserting these ansatz functions (15.95) and (15.96) into the above

diﬀerential equations (15.90)–(15.92), one obtains:

2(B −A)

= 0 (15.97)

−

4(B −A)

(15.98)

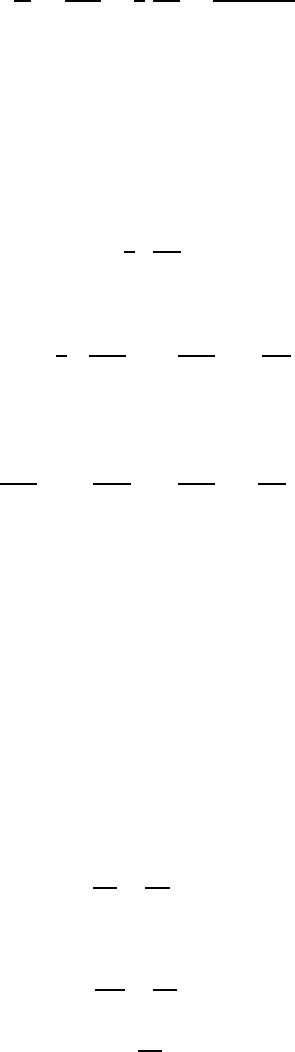
448 15 Fluid Flows of Small Reynolds Numbers

2(B −A)

. (15.99)

From the boundary conditions for ﬂows around spheres, the following

boundary conditions result for the functions A, B and C:

A(R)=0,B(R)=0,A(∞)=U

∞

, and B(∞)=U

∞

. (15.100)

The solution steps for the diﬀerential equations (15.97)–(15.99) can be stated

as follows

From (15.97) it follows that:

A =

+ B. (15.101)

Inserting A into (15.99) results in:

C =

+3r

. (15.102)

This diﬀerential equation can be diﬀerentiated with respect to r and the

result can be inserted into (15.98) to yield:

+8r

− 8

=0. (15.103)

The resulting Euler diﬀerential equation can be solved by integration with

particular solutions being sought of the form B = cr

.IfoneinsertsB = cr

into the above diﬀerential equations, an equation of fourth order for k results:

k(k −1)(k − 2)(k − 3) + 8k(k −1)(k − 2) + 8k(k −1) − 8k =0

or, written in a somewhat simpliﬁed form:

k(k − 2)(k +3)(k + 1) = 0 (15.104)

so that the following k-values result as solutions:

k =0,k=2,k= −3andk = −1. (15.105)

Thus, for B(r) the following general solution can be given:

B(r)=

+ C

. (15.106)

From the equations for A(r) (15.101) and C(r) (15.102) one obtains:

A(r)=−

+ C

+2C

(15.107)

C(r)=

+10C

r. (15.108)

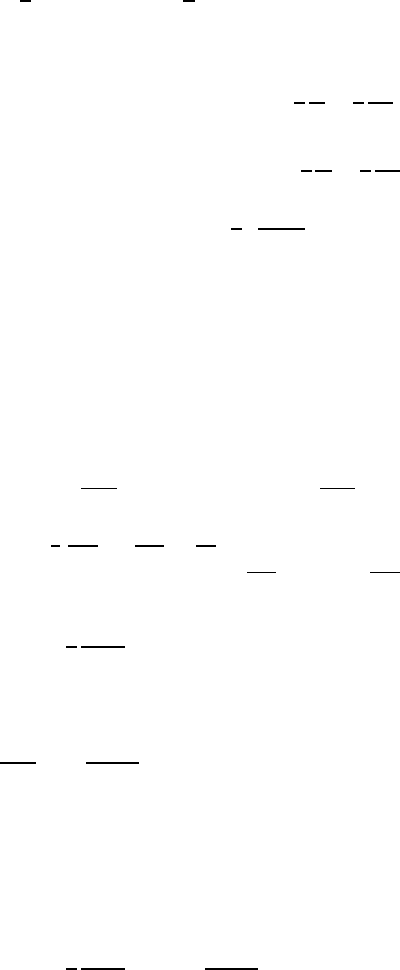
15.6 The Slow Translatory Motion of a Sphere 449

Inserting for A(r), B(r)andC(r) the boundary conditions (15.100), the

integration constants C

, C

and C

can be determined:

∞

; C

= −

∞

R; C

= U

∞

; C

=0. (15.109)

Thus, for U

(r, θ), U

(r, θ)andP (r, θ) the following solutions result:

(r, θ)=U

∞

cos θ



1 −



(15.110)

(r, θ)=−U

∞

sin θ



1 −

−



(15.111)

P (r, θ)=−

∞

cos θ. (15.112)

With these relationships, the solution for the velocity and pressure ﬁelds for

the ﬂow around a sphere are available. Although obtained by solving a set of

simpliﬁed diﬀerential equations, which was obtained as a reduced set from the

Navier–Stokes equations by neglecting the acceleration terms, an important

set of results emerged for U

, U

and P. However, the solutions obtained hold

only for Re < 1.

When looking at the diﬀerent momentum transport terms τ

and τ

rθ

the ﬂow problem discussed here, one obtains for ρ = constant:

= −µ



∂U

∂r



for r = R is



∂U

∂r



r=R

= 0 (15.113)

and τ

r,θ

= − µ

∂U

∂θ

∂U

∂r

−

. From this, one obtains for r = R,be-

cause U

= U

= 0 and therefore also

∂U

∂θ

=0and

∂U

∂θ

=0,atthesurface

of the sphere the following expression for the pressure:

P =

µU

∞

cos θ (acts on each point vertically (15.114)

to the surface of the sphere).

In addition,

r,θ

= −µ

∂U

∂r

= −

3µU

∞

sin θ (acts on each point tangentially (15.115)

to the surface of the sphere).

The drag force F

can thus be computed:

(P cos θ − τ

r,θ

sin θ)dF (15.116)

= −



µU

∞

cos

θ +

3µU

∞

sin



2πR

sin θ

dθ (15.117)

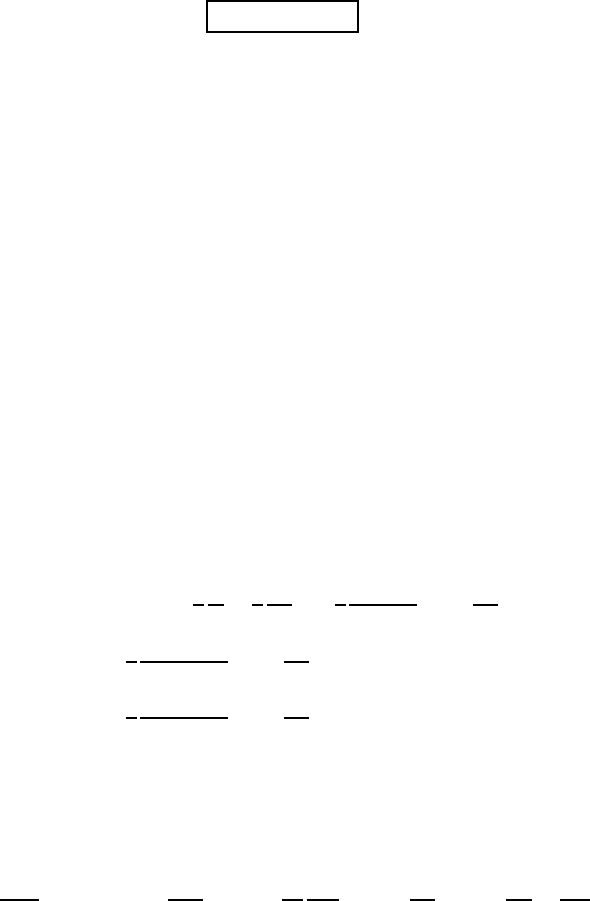
450 15 Fluid Flows of Small Reynolds Numbers

or rewritten and integrated:

= −

3πµU

∞

R(sin θ)dθ = −3πµU

∞

R (−cos θ)

(15.118)

F = −6πµU

∞

R .

The integration over the pressure acting on the surface of the sphere, and

over the momentum loss to the wall, yields the Stokes drag force W. Here it

is of interest that the share of force coming from the pressure:

= −

P cos θ2πR

sin θ dθ = −3πµU

∞

cos

θ sin θ dθ (15.119)

with F

= − 2πµU

∞

R amounts only to one-third of the total drag, i.e. two-

thirds of the drag force results thus from the molecular momentum input

to the surface of the sphere. This underlines the importance that must be

attached to the viscosity terms in the Navier–Stokes equations for the solution

of practical ﬂow problems at small Reynolds numbers.

In order to determine now the velocity components in Cartesian coordi-

nates, i.e. U

, U

and U

, the following equations for the transformation of

coordinates are employed:

= r cos θ ; U

= U

cos θ − U

sin θ (15.120)

= r sin θ cos φ ; U

= U

sin θ cos φ + U

cos θ cos φ − U

sin φ (15.121)

= r sin θ sin φ ; U

= U

sin θ sin φ + U

cos θ sin φ + U

cos φ.(15.122)

With these equations one obtains:

= U

∞



1 −

−



−

∞



1 −



(15.123)

= −

∞



1 −



(15.124)

= −

∞



1 −



. (15.125)

For the solution of the Stokes ﬂow around spheres, the above simpliﬁed ﬂow

equations (15.90)–(15.92) were employed. To be able to assess how large the

neglected terms of the Navier–Stokes equations are in comparison with the

terms considered in the solution, the acceleration:





θ=0

= ρ



∂U

∂r



θ=0

3ρ

∞



1 −



1 −



(15.126)