Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

410 14 Time-Dependent Flows

Application of boundary condition (14.96) yields

A exp (−λ

τ)J

(λ) = 0 (14.112)

Since setting A = 0 would result in a trivial solution, one must require

(λ) = 0 (14.113)

for the non-trivial solution. Therefore, one obtains multiple values of λ that

satisfy the boundary conditions at the wall. The values of λ obtained from

(14.113) are the 0-values of the zeroth order of Bessel functions of the ﬁrst

kind. From tables of Bessel functions, the solutions of (14.113) are obtained

as follows:

=2.405, 5.520, 8.654, 11.792, 14.931, 18.071, 21.212, 24.353, 27.494

(14.114)

Each of the solutions of λ

now constitutes an individual solution. Con-

sidering the linearity of the governing equations (14.94) and (14.97), the

complete solution for U

∗

(η, τ) is obtained by linear superposition:

∗

(η, τ)=

∞



n=1

exp (−λ

τ)J

(λ

η) = 0 (14.115)

For readers of this book, the values for J

(α)andY

(α)canbetaken

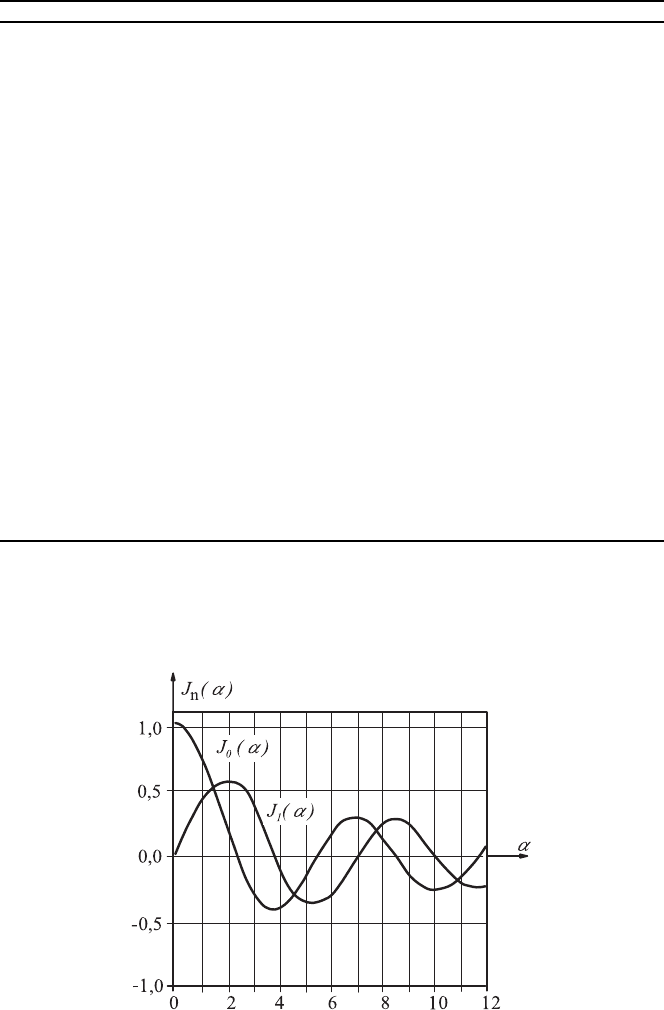
from Tables 14.1 and 14.2. The function J

(α)andJ

(α) are also given in

Fig. 14.6, Y

(α)andY

(α) in Fig. 14.7.

In order to be able to insert the boundary conditions, it is further necessary

to perform the derivatization dU

∗

/dη. For this it is important to know that

for the following relationship for the derivative holds:

(α)

= −J

(α)

dα

(14.116)

Thus one can write

∗

dη

= −

∞



n=1

exp

−λ

(λ

η) (14.117)

Now the boundary conditions can be implemented:

η =1 ; U

∗

=0 ; J

(λ

) = 0 (14.118)

and thus the following λ

values can be determined as already explained

above:

=2.405, 5.520, 8.654, 11.792, 14.931, 18.071, 21.212, 24.353, 27.494

(14.119)

14.2 Accelerated and Decelerated Fluid Flows 411

Table 14.1 Discrete values of Bessel functions of the ﬁrst kind

αJ

(α) J

(α) αJ

(α) J

(α) αJ

(α) J

(α)

0.00 +1.000 0.000 5.00 −0.178 −0.328 10.00 −0.246 +0.435

0.20 +0.990 +0.099 5.20 −0.110 −0.343 10.20 −0.250 −0.007

0.40 +0.960 +0.196 5.40 −0.041 −0.345 10.40 −0.243 −0.056

0.60 +0.912 +0.287 5.60 +0.027 −0.334 10.60 −0.228 −0.101

0.80 +0.846 +0.369 5.80 +0.092 −0.311 10.80 −0

.203 −0.142

1.00 +0.765 +0.440 6.00 +0.151 −0.277 11.00 −0.171 −0.177

1.20 +0.671 +0.498 6.20 +0.202 −0.233 11.20 −0.133 −0.204

1.40 +0.567 +0.542 6.40 +0.243 −0.182 11.40 −0.090 −0.223

1.60 +0.455 +0.570 6.60 +0.274 −0.125 11.60 −0.045 −0.232

1.80 +0.340 +0.582 6.80 +0.293 −0

.065 11.80 +0.002 −0.232

2.00 +0.224 +0.577 7.00 +0.300 −0.005 12.00 +0.048 −0.223

2.20 +0.110 +0.556 7.20 +0.295 +0.054 12.20 +0.091 −0.206

2.40 +0.003 +0.520 7.40 +0.279 +0.110 12.40 +0.130 −0.181

2.60 −0.097 +0.471 7.60 +0.252 +0.159 12.60 +0.163 −0.149

2.80 −0.185 +0.410 7.80 +0.215 +0.201 12.80 +0.189 −0.111

3.00 −

0.260 +0.339 8.00 +0.172 +0.235 13.00 +0.207 −0.070

3.20 −0.320 +0.261 8.20 +0.122 +0.258 13.20 +0.217 −0.027

3.40 −0.364 +0.179 8.40 +0.069 +0.271 13.40 +0.218 +0.016

3.60 −0.392 +0.096 8.60 +0.015 +0.273 13.60 +0.210 +0.059

3.80 −0.403 +0.013 8.80 −0.039 +0.264 13.80 +0.194 +0.098

4.00 −0.397 −0.066 9.00 −

0.090 +0.245 14.00 +0.171 +0.133

4.20 −0.377 −0.139 9.20 −0.137 +0.217 14.20 +0.141 +0.163

4.40 −0.342 −0.203 9.40 −0.177 +0.182 14.40 +0.106 +0.185

4.60 −0.296 −0.257 9.60 −0.209 +0.140 14.60 +0.068 +0.200

4.80 −0.240 −0.299 9.80 −0.232 +0.093 14.80 +0.027 +0.206

5.00 −0.178 −0.

328 10.00 −0.246 +0.435 15.00 −0.014 +0.205

Fig. 14.6 Bessel function of the ﬁrst kind

412 14 Time-Dependent Flows

From the initial condition of the considered ﬂow problem, one obtains

τ =0 ; U

∗

(η, 0) = 1 =

∞



n=1

(λ

η) (14.120)

i.e. no λ

n=0

exists and one thus obtains

∗

(η, 0) = 1 = A

(λ, η)+A

(λ

η)+···A

(λ

η)+··· (14.121)

For determining the constants A

one uses a special property of the Bessel

function:

(ax)J

(bx)dx =0 whena = b (14.122)

but

(ax)dx = 0 i.e. when a = b (14.123)

Table 14.2 Discrete values of Bessel functions of the a second kind

αY

(α) Y

(α) αY

(α) Y

(α) αY

(α) Y

(α)

0.00 −∞ −∞ 5.00 −0.309 +0.148 10.00 +0.058 +0.249

0.20 −1.081 −3.324 5.20 −0.331 +0.079 10.20 +0.006 +0.250

0.40 −0.606 −1.781 5.40 −0.340 +0.010 10.40 −0.044 +0.242

0.60 −0.309 −1.260 5.60 −0.335 +0.057 10.60 −0.090 +0.224

0.80 −0.087 −0.978 5.80 −0.318 −0.119 10.80 −0

.133 +0.197

1.00 +0.088 −0.781 6.00 −0.288 −0.175 11.00 −0.169 +0.164

1.20 +0.228 −0.621 6.20 −0.248 −0.222 11.20 −0.198 +0.124

1.40 +0.338 −0.479 6.40 −0.200 −0.260 11.40 −0.218 +0.081

1.60 +0.420 −0.348 6.60 −0.145 −0.286 11.60 −0.230 +0.035

1.80 +0.477 −0

.224 6.80 −0.086 −0.300 11.80 −0.232 −0.012

2.00 +0.510 −0.107 7.00 −0.026 −0.303 12.00 −0.225 −0.057

2.20 +0.521 +0.002 7.20 +0.034 −0.293 12.20 −0.210 −0.099

2.40 +0.510 +0.101 7.40 +0.091 −0.273 12.40 −0.186 −0.137

2.60 +0.481 +0.188 7.60 +0.142 −0.243 12.60 −

0.155 −0.169

2.80 +0.436 +0.264 7.80 +0.187 −0.204 12.80 −0.119 −0.194

3.00 +0.377 +0.325 8.00 +0.224 −0.158 13.00 −0.078 −0.210

3.20 +0.307 +0.371 8.20 +0.250 −0.107 13.20 −0.035 −0.218

3.40 +0.230 +0.401 8.40 +0.266 −0.054 13.40 +0.009 −0.218

3.60 +0.148 +0.415 8.60 +0.272 +0.001 13.60 +0.

051 −0.208

3.80 +0.645 +0.414 8.80 +0.266 +0.054 13.80 +0.091 −0.191

4.00 −0.017 +0.380 9.00 +0.250 +0.104 14.00 +0.127 −0.167

4.20 −0.094 +0.368 9.20 +0.225 +0.149 14.20 +0.158 −0.136

4.40 −0.163 +0.326 9.40 +0.191 +0.187 14.40 +0.181 −0.100

4.60 −0.224 +0.274 9.60 +0.150 +0.217 14.60 +0.197 −0.061

4.80 −0

.272 +0.214 9.80 +0.105 +0.238 14.80 +0.206 −0.020

5.00 −0.309 +0.148 10.00 +0.058 +0.249 15.00 +0.206 +0.021

14.2 Accelerated and Decelerated Fluid Flows 413

Fig. 14.7 Bessel function of the second kind

Thus the coeﬃcients A

···A

. ··· in (14.117) can be determined by

successive multiplication by ηJ

(λ

η) and by the following integration:

ηJ

(λ

η)dη =

ηJ

(λ

η)dη (14.124)

Thus for each of the coeﬃcients A

the following relationship results:

ηJ

(λ

η)dη

ηJ

(λ

η)dη

(14.125)

Carrying out a ﬁrst step of the integration yields:

(λ

)+J

(λ

)]

ηJ

(λ

η)dη (14.126)

By further integration one obtains:

(λ

)

(λ

)+J

(λ

))

(14.127)

Thus for the velocity distribution according to (14.111), the following expres-

sion results:

∗

(η, τ)=

∞



n=1

(λ

)

(λ

)+J

(λ

)

exp

−λ

(λ

η) (14.128)

414 14 Time-Dependent Flows

For the gradient of the velocity proﬁle one obtains according to (14.117):

∂U

∗

∂η

(η, τ)=−

∞



n=1

(λ

)

(λ

)+J

(λ

)

exp

−λ

(λ

η) (14.129)

Considering that

(λ

η)

dη

= −J

(λ

η) λ

is valid over the entire ﬂow ﬁeld,

one can employ the above results to determine the shear-stress distribution

for the considered ﬂow problem:

= −µ



−

∗

dη



µU

∗

dη

(14.130a)

and thus τ

is given by

= −

µU

∞



n=1

(λ

)

(λ

)+J

(λ

))

exp

−λ

(λ

η) (14.130b)

For the τ

value at the pipe wall, i.e. with η =1,oneobtains

(R, t)=−µ

∞



n=1

1+(J

(λ

) /J

(λ

))

exp(−λ

)

νt

(14.131)

i.e. a ﬁnite value, even for time t = 0. This is a surprising result when

comparing it with τ

→∞for t = 0 for the induced channel ﬂow.

14.3 Oscillating Fluid Flows

14.3.1 Stokes Second Problem

For further deepening the physical understanding of unsteady ﬂuid move-

ments, induced by momentum diﬀusion, those ﬂuid movements which occur

due to an oscillating plate will be discussed in this section. Hence, a ﬂuid ﬂow

problem is considered which comes about due to the oscillatory movement

of a plate in a such way that the ﬂuid movement created in the immediate

vicinity of the plate is communicated to the ﬂuid above the plate, by molec-

ular momentum diﬀusion. The movement of the ﬂuid above the plate is thus

governed by the following partial diﬀerential equation:

∂U

∂t

= ν

∂

∂x

(14.132)

Hence the same diﬀerential equation as in the previous sections describes

this ﬂow. Its particular features are introduced by the imposed initial and

boundary conditions.

14.3 Oscillating Fluid Flows 415

The initial and boundary conditions of the problem can be stated as

follows:

for all times t ≤ 0:U

,t) = 0 (14.133)

for all times t>0:

=0 ; U

(0,t)= U

cos(ωt) (14.134)

→∞ ; U

(∞,t) = 0 (14.135)

Again, a solution is sought which can be found by the following ansatz, i.e.

by separation of the variables:

,t)=f (x

)g(t) (14.136)

Inserting in (14.132) results in:

= νg

(14.137)

By separation of the variables one can derive:

νg

= ±iλ

(14.138)

In (14.138), the constant appearing on the right-hand side was set to read

±iλ

with i =

√

−1. This takes into consideration the fact that according

to (14.134), there is a periodic stimulation of the ﬂuid movement. Thus co-

sine and sine terms are expected in the solution, which can be expressed

by complex terms in the exponential function. Consequently, the following

diﬀerential equations have to be solved:

−

±iλ

νg = 0 (14.139)

−

±iλ

f = 0 (14.140)

The solutions of these two diﬀerential equations yields for U

,t):

,t)=C

∗

exp

±iλ

νt ± λ

√

±ix

(14.141)

Because of the combination of positive and negative signs, four solutions

result:

= A exp



−

√

+ i



νt −

√



(14.142)

= B exp



−

√

− i



νt −

√



(14.143)

= C exp



√

+ i



νt −

√



(14.144)

= D exp



√

− i



νt +

√



(14.145)

416 14 Time-Dependent Flows

The last two partial solutions of the diﬀerential equations do not represent

reasonable results from a physical point of view because of the requirement

(14.135), as for x

→∞they yield for the velocity U

(∞,t) →∞.Thusasa

solution ansatz, that is physically meaningful, the following results:

,t)=U

,t)+U

,t) (14.146)

i.e.

,t)=exp



−

√

<

∗

exp





νt −

√



+ B

∗

exp



−i



νt −

√

=

(14.147)

The expressions in the curly brackets can be written as cosine and sine

functions:

,t)=exp



−

√



A cos



νt −

√



+ B sin



νt −

√



(14.148)

Applying the boundary condition (14.134), one obtains

(0,t)=U

cos(ωt)=A cos(λ

νt)+B sin(λ

νt) (14.149)

and thus B =0,A = U

and λ =



ω/ν so that one obtains as a solution

,t)=U

exp



−

2ν



cos



ωt −

2ν



(14.150)

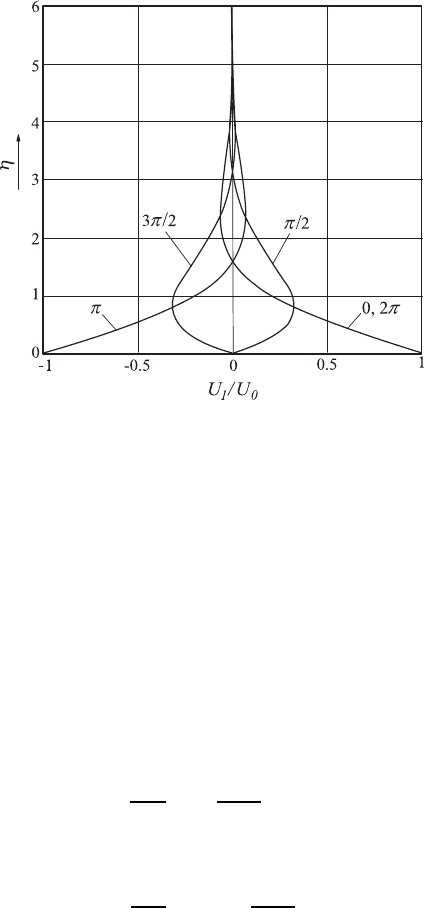
This equation describes the velocity distributions stated for certain ωt val-

ues in Fig. 14.8 which are present in the ﬂuid above the plate. In Fig. 14.8,

velocities are given for ωt =0,

,π,

3π

, 2π.

The velocity distributions indicated in Fig. 14.8 show that the ﬂuid move-

ment in ﬂuid layers, some distance away from the wall, always lags behind the

movement of the plate. The amplitude of the ﬂuid movement decreases with

increasing distance from the plate. At the plate itself, the ﬂuid movement

follows exactly the movement of the plate, i.e. speciﬁcations existing due to

the boundary conditions are fulﬁlled.

The above-mentioned phase shift is of great interest for a number of

ﬂuid motions. For practical purposes, one can state that a perceivable ﬂuid

movement can only be observed for

≤ 2π

√

(14.151)

The larger the kinematic viscosity of the ﬂuid is, the thicker this layer

becomes. Moreover, the relationship (14.151) says that high-frequency os-

cillations can penetrate less deep into the ﬂuid interior than low-frequency

oscillations. These kinds of results of the analytical considerations above give

important insights that can be used advantageously in considerations of many

externally induced ﬂuid ﬂows.

14.4 Pressure Gradient-Driven Fluid Flows 417

Fig. 14.8 Velocity proﬁles above an oscillating plane plate at ﬁxed phases of the

plate motion

14.4 Pressure Gradient-Driven Fluid Flows

14.4.1 Starting Flow in a Channel

The considerations below were carried out in order to investigate the inﬂuence

of viscosity on the channel ﬂow, setting in due to gravitational forces. It

is assumed that the entire ﬂuid in the channel in Fig. 14.9 is at rest for

t<0. At time t = 0, the ﬂuid is set in motion, namely by the gravitational

acceleration g. The setting in, non-stationary ﬂuid ﬂow is described by the

following diﬀerential equation:

∂U

∂t

= µ

∂

∂x

+ ρg (14.152)

This diﬀerential equation can be rewritten as

∂U

∂t

= g + ν

∂

∂x

(14.153)

This equation has to be solved for the following initial and boundary

conditions:

Initial condition:

for t ≤ 0 U

,t) = 0 (14.154)

for t>0 ; U

=0 for −D<x

< +D (14.155)

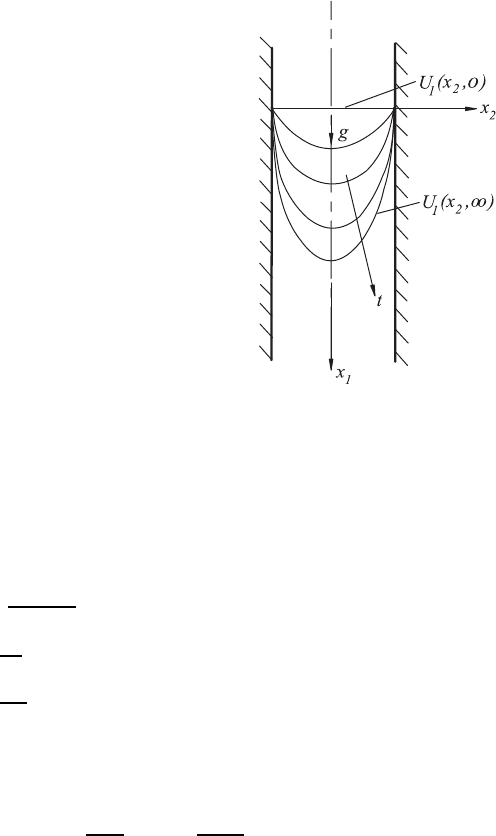
418 14 Time-Dependent Flows

Fig. 14.9 Starting ﬂow in a channel

The boundary conditions are:

=0 for x

= ±D (14.156)

To solve the partial diﬀerential equation (14.153), it is recommended to

introduce the following dimensionless variables:

∗

/2ν

dimensionless velocity (14.157)

η =

= x

∗

dimensionless position coordinate (14.158)

τ =

νt

= t

∗

dimensionless time (14.159)

On inserting these dimensionless quantities in (14.153), one obtains the par-

tial diﬀerential equation (14.160) for the above-introduced dimensionless

velocity U

∗

∂U

∗

∂τ

=2+

∂

∗

∂η

(14.160)

with the initial and boundary conditions formulated for the dimensionless

variables as follows:

initial conditions: τ ≤ 0: U

∗

=0for − 1 <η<+1

boundary conditions: η =+1:U

∗

=0forallτ>0

η = −1:U

∗

=0forallτ>0

(14.161)

When looking for a solution of the partial diﬀerential equation (14.160), the

approach is to look for the stationary solution U

∗

∞

(occurring for τ →∞)

and for the non-stationary part U

∗

, to yield generally

14.4 Pressure Gradient-Driven Fluid Flows 419

∗

= U

∗

∞

− U

∗

(14.162)

Due to the stationarity of the ﬂow for τ →∞, one obtains the following

partial diﬀerential equation for U

∗

∞

0=2+

∂

∗

∞

∂η

(14.163)

Taking into consideration the above boundary conditions, the following

results for U

∗

∞

∗

∞

=(1− η

) (14.164)

On introducing U

∗

=(1− η

) − U

∗

into the diﬀerential equation (14.160),

one obtains a diﬀerential equation to be solved for U

∗

∂U

∗

∂τ

∂

∗

∂η

(14.165)

with the following initial condition and the boundary condition:

τ =0:U

∗

= U

∗

∞

(14.166)

τ>0:U

∗

=0forη = ±1 (14.167)

With the ansatz for a solution by separation of variables:

∗

= f(η)g(τ) (14.168)

one obtains

∂U

∗

∂τ

= f

dτ

and

∂

∗

∂η

= g

dη

(14.169)

and by insertion in (14.165):

dτ

dη

(14.170)

As this equation can on the left-hand side be only a function of τ andonthe

right-hand side only a function of η, the diﬀerential equation can be fulﬁlled

only by setting both sides equal to a constant:

dτ

= −λ

; g = A exp

−λ

(14.171)

dη

= −λ

; f = B cos(λη)+C sin(λη) (14.172)

where A, B and C are the constants introduced by the integration. When

considering the coordinate system sketched in Fig. 14.9 and quantitatively

described in Fig 14.10, yielding a solution that is symmetrical with regard to