Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

13.7 Pipe Flow (Hagen–Poiseuille Flow) 379

13.7 Pipe Flow (Hagen–Poiseuille Flow)

The laminar fully developed pipe ﬂow is another important ﬂuid ﬂow which

can be treated as stationary, one-dimensional ﬂow, i.e. by solving the following

diﬀerential equation:

−

dΠ

+ µ





+ ρg

=0. (13.94)

When considering the horizontal pipe ﬂow as indicated in Fig. 13.9, the

following simpliﬁed diﬀerential equation holds, as g

=0:







dΠ



r. (13.95)

This equation expresses the fact that the external pressure gradient im-

posed on the ﬂuid is maintained in equilibrium by viscous forces acting also

on the ﬂuid, so that a non-accelerated ﬂow results.

The boundary conditions for this ﬂow are:

r =0;

= 0 and for r = R; U

=0.

The ﬂow occurring in the cylindrical pipe indicated in Fig. 13.9 requires a

pressure gradient to be maintained in the developed state ( dΠ/z), i.e. this

quantity has to be applied externally for a pipe ﬂow to be established. For

the resultant ﬂow velocity one obtains the following diﬀerential equation:







dΠ



r. (13.96)

Pipe wall

Parabolic velocit

profile

Fig. 13.9 Laminar ﬂow in a pipe

380 13 Incompressible Fluid Flows

By a ﬁrst integration of (13.96), the following results:

2µ



dΠ



r +

. (13.97)

By a second integration one obtains:

4µ



dΠ



+ C

ln r + C

. (13.98)

Applying the boundary conditions:

r → 0;

→ 0andr = R : U

=0. (13.99)

and C

can be determined:

=0 and C

= −

4µ



dπ



. (13.100)

Thus the equation for the velocity distribution U

(r) for the laminar pipe

ﬂow reads:

= −

4µ



dΠ



1 −







. (13.101)

The velocity proﬁle is parabolic and U

is positive; the minus sign takes into

account the presence of a negative pressure gradient in the z direction, i.e.

the pressure decreases in the +z direction and the ﬂuid thus ﬂows in that

direction.

The volume ﬂow through the pipe (volume per unit time) can be

computed as follows:

Q =

2πrU

dr = −

πR

8µ



dΠ



(13.102)

or rewritten:



dΠ



∆p

∆z

= −

8µ

πR

. (13.103)

In the case of a laminar pipe ﬂow, the pressure drop per unit pipe length is

proportional to the dynamic viscosity of the ﬂowing ﬂuid and the volume ﬂow

rate, as well as inversely proportional to the fourth power of the pipe radius.

The mean velocity results as:

U =

πR

= −

8µ



dΠ



. (13.104)

The above connection between the volume ﬂow, the inner radius R of the pipe,

the viscosity of the ﬂow medium and the resultant pressure gradient is known

13.7 Pipe Flow (Hagen–Poiseuille Flow) 381

as the Hagen–Poiseuille law. It was found by Hagen in 1839 and by Poiseuille

in 1840/41 independently of one another in experimental investigations. The

experimental conﬁrmation of the above-derived relations stresses the validity

of the assumptions made for the pipe ﬂow and beyond that the fact that the

validity of the Navier–Stokes equations for the description of ﬂuid ﬂows of

Newtonian media hold.

The momentum loss to the wall of the pipe, due to the laminar, fully

developed pipe ﬂow, can be computed as

= −µ







dΠ



R. (13.105)

The friction coeﬃcient can thus be calculated as follows:

2τ

(2R)

Uµ

U2R



dΠ



R(2R)



dΠ



, (13.106)

i.e. we obtain the following functional relationship:

with Re =

U2R

. (13.107)

The representation of the friction coeﬃcient as function of the Reynolds num-

ber yields, in a diagram with double-logarithmic axes, a straight line with the

gradient (−1).

Further insight into the ﬂuid ﬂow and the molecule interactions, taking

place in viscous mediums, can be gained by computing the energy dissipation

in the pipe ﬂow by the action of the ﬂuid viscosity. Based on the general

relationship for the energy dissipation per unit volume in a Newtonian ﬂuid,

one obtains:

diss

=2µ



∂U

∂r





∂U

∂ϕ





∂U

∂z



+µ



∂

∂r







dϕ



+ µ





∂U

∂ϕ





∂U

∂z



+µ



∂U

∂z





∂U

∂r



. (13.108)

When considering all the simpliﬁcations which were introduced for the

derivation of (13.94), the above general relationship for the energy dissipation

of a viscous pipe ﬂow can be described as follows:

diss

= µ



∂U

∂r



= µ





. (13.109)

382 13 Incompressible Fluid Flows

By introducing dV =2πr dz dr, one obtains

diss

= µ





2πr dz dr. (13.110)

/dr can be written as:

= −

2µ



dΠ



r. (13.111)

Thus the dissipated energy per unit length of a pipe ﬂow can be calculated

as:

diss

2µ



dΠ



dr. (13.112)

On integrating this equation, one obtains the energy dissipated per unit pipe

length dz:

diss

2µ



dΠ



dr =

8µ



dΠ



, (13.113)

i.e. the pressure gradient that has to be applied per unit length of the pipe

serves for supplying the mechanical energy dissipated into heat, per unit

length of the ﬂuid motion. Considering:

Q =

πR

8µ



dΠ



, (13.114)

(13.113) can be written as:

diss



dΠ



or ∆E

diss

Q∆P

diss

. (13.115)

This relationship expresses that the pressure gradient to be applied per

unit length of the pipe corresponds to the energy dissipated per unit length

of the pipe and per unit volume ﬂow:

dΠ

diss

. (13.116)

The validity of the above-derived relationships for the pipe ﬂow is, however,

limited to laminar ﬂows, i.e. to Reynolds numbers which are smaller than

crit

. This critical Reynolds number is for pipe ﬂows in the range

crit

U2R

 2.3to2.5 × 10

. (13.117)

When the Reynolds number of a pipe ﬂow is larger than this critical value,

and when no special precautions are taken to keep ﬂow perturbations away

13.8 Axial Flow Between Two Cylinders 383

from the pipe ﬂow, then the ﬂow in the range of the critical Reynolds number

changes abruptly from laminar to turbulent. In this case there is no longer

a directed ﬂow present as described by the above relationships. The ﬂow

in the pipe shows, superimposed on a mean ﬂow ﬁeld, stochastic velocity

ﬂuctuations which lead to an additional momentum transport transverse to

the ﬂow direction. This momentum transport is not covered by the above

basic equations.

The most important properties of turbulent pipe-channel ﬂows are in-

dicated in Chap. 18 and some references are made to deviations from the

laminar pipe ﬂow as discussed here.

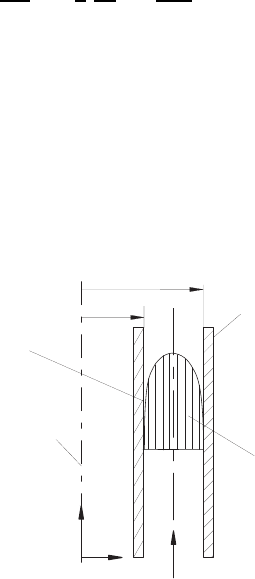
13.8 Axial Flow Between Two Cylinders

In chemical engineering, there are a large number of axially symmetric appa-

ratus in which ﬂows can be treated as stationary, fully developed ﬂows. They

are described by the following partial diﬀerential equation:

−

dΠ

+ µ

∂

∂r



∂U

∂r



+ ρg

=0. (13.118)

Annular axial ﬂows are among them, of the kind sketched in Fig. 13.10;

the boundary conditions for this ﬂow can be given as:

for r = R

: U

= 0 and for r = R

: U

=0.

As an interesting example, the ﬂow in a cylindrical annular channel, as

shown in Fig. 13.10, will be discussed here. The annular channel is formed by

two axially positioned pipes having radii R

and R

Inside wall

Axis

r = 0

Outside wall

Velocity

profile

Fig. 13.10 Upwards ﬂow for a cylindrical annular clearance

384 13 Incompressible Fluid Flows

For further simpliﬁcation of the derivation,

K = R

,Π

∗

= Π + ρgz (13.119)

are introduced. Considering the coordinate system indicated in Fig. 13.10,

= −g holds and thus one obtains the following form of the diﬀerential

equation describing the annular channel ﬂow of Fig. 13.10

∂

∂r



∂U

∂r



∂

∂z

(Π + ρgz)=

∂Π

∗

∂z

. (13.120)

Taking into account the assumptions

∂

∂z

(···) = 0 for the ﬂow ﬁeld, i.e. as-

suming a fully developed ﬂow in the z direction, the above-mentioned partial

diﬀerentials can be written as total diﬀerentials, as follows:





dΠ

∗

r. (13.121)

In Sect. 13.6, it was shown that this equation has the following general

solution:

4µ

dΠ

∗

+ C

ln r + C

. (13.122)

Based on the boundary conditions stated in Fig. 13.10, the integration con-

stants C

and C

for the ﬂow in a cylindrical annular clearance can be

determined by (13.123) and (13.124).

From the boundary condition r = R

; U

= 0 results the ﬁrst equation for

the computation of the integration constants C

and C

0=R

+ C

ln R

+ C

. (13.123)

On considering r = R

; U

=0,oneobtains:

0=R

+ C

ln R

+ C

, (13.124)

the second relationship for the computation of the integration constants C

and C

. In this way, one arrives at:

= R

1 −





ln (R

)

(13.125)

or, considering K = R

= R

(1 − K

)

ln K

. (13.126)

results as

= R



− 1)

ln K



ln R

− 1. (13.127)

13.8 Axial Flow Between Two Cylinders 385

For the velocity distribution, the following equation results:

= −

4µ



dΠ

∗



3

1 −





− 1

ln K

× ln





. (13.128)

The above equation shows that for K → 0 the velocity distribution for the

fully developed pipe ﬂow is not obtained. The position of the maximum

velocity is computed as

r =(u

= u

max

)=R

1 − K

2ln(1/K)

. (13.129)

The maximum velocity is thus computed from the equation for U

)

max

= −

4µ



dΠ

∗





1 −



1 − K

2ln(1/K)



1 − ln



1 − K

2ln(1/K)



(13.130)

Thevolumeﬂowresultsas

Q = −

∗

8µ

dΠ

∗



1 − K

−

(1 − K

)

ln (1/K)



(13.131)

and for the mean velocity one obtains

π (R

− R

)

8µ



dΠ

∗





1 − K

−

1 − K

ln (

/K)



. (13.132)

The molecular momentum transport can be computed as

r,z



dΠ

∗







−



1 − K

2ln(1/K)





. (13.133)

The quantity τ

r,z

is naturally at the position du

/dr = 0, i.e. at U

= U

max

equal to zero, so that one obtains from (13.133):

r (τ

r,z

=0)=R

1 − K

2ln(1/K)

. (13.134)

For the annular clearance it also holds that the above relationships can only

be employed for laminar ﬂows. The additional momentum transports, occur-

ring in turbulent ﬂows due to the turbulent velocity ﬂuctuations, were not

taken into consideration in the above equations. Therefore, the derived equa-

tions in this section can be employed only when it has been conﬁrmed that

the ﬂow in the considered annular channel ﬂows in a laminar way.

386 13 Incompressible Fluid Flows

13.9 Film Flows with Two Layers

The problems of steady, two-dimensional and fully developed ﬂows of incom-

pressible ﬂuids, discussed in the previous chapters, can be extended to ﬂuid

ﬂows that comprise of several non-mixable ﬂuids. The derived basic equations

for fully developed ﬂows have to be solved, in the presence of several ﬂuids,

for each ﬂuid ﬂow and the boundary conditions existing in the inter-layers of

the ﬂuids have to be considered in the solutions. This is shown below for a

ﬁlm ﬂow made up of two layers.

In coating technology, it is customary to insert superimposed ﬁlm ﬂows

of non-mixable ﬂuids in order to coat several ﬁlms, in one process step, on

to a substrate. In practice, up to 20 layers can be simultaneously applied

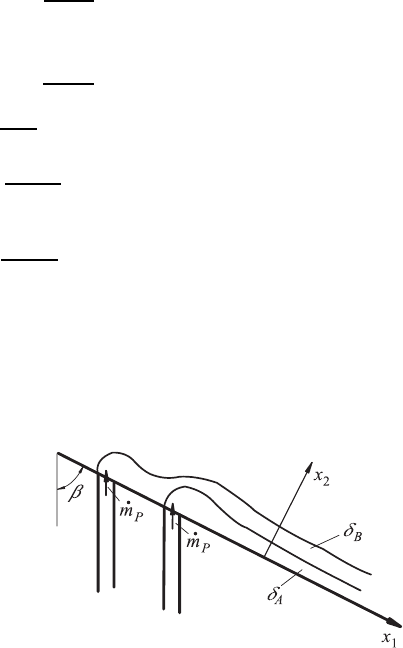
with high accuracy. If one limits oneself to two layers, ﬂow conﬁgurations as

shown in Fig. 13.11 develop. The ﬁgure shows two superimposed ﬁlm ﬂows

which are moved by gravitation on top of a plane inclined wall. Flows of this

kind are described by the following diﬀerential equations:

0=µ

+ ρ

(13.135)

and

0=µ

+ ρ

(13.136)

with g

= g cos β and ν

A,B

, so that one obtains by integration:

= −



g cos β

2ν



+ C

(13.137)

and

= −



g cos β

2ν



+ C

. (13.138)

By this integration, four integration constants were introduced in the above

relationships which have to be determined by appropriate boundary con-

ditions:

=0 ; U

= 0 (no-slip wall condition) ; C

=0, (13.139)

Fig. 13.11 Flow between ﬂuid ﬁlms

on top of a plane, inclined wall

13.9 Film Flows with Two Layers 387

= δ

+ δ

;

= 0 (free surface), (13.140)

= δ

; U

= U

and also µ

= µ

. (13.141)

From the boundary condition for the free surface, C

results as:

g cos β

(δ

+ δ

) . (13.142)

The equality of the local ﬁlm velocities in the common interface between the

ﬁlms yields:

−

g cos β

2ν

+ C

= −

g cos β

2ν

g cos β

(δ

+ δ

) δ

+ C

. (13.143)

The equality of the local momentum transport terms in the common interface

between the ﬁlms further yields:

−δ

g cos βδ

+ C

= −ρ

g cos βδ

+ ρ

g cos β(δ

+ δ

). (13.144)

From the above equation, one can deduce:

=(ρ

+ ρ

)g cos β (13.145)

and for C

,oneobtains:

= −g cos β

+ ν

+(ρ

+ ρ

) g cos β −

g cos β

(δ

+ δ

) δ

(13.146)

Thus, one obtains for the velocity distributions U

and U

= −



g cos β

2ν



+[(ρ

+ ρ

) β] x

for 0 ≤ x

≤ δ

(13.147)

and

= −



g cos β

2ν



g cos β

2ν

(δ

+ δ

) x

−g cos β

+ ν

2ν

+(ρ

+ ρ

) g cos β

−

g cos β

(δ

+ δ

) δ

for δ

≤ x

≤ δ

. (13.148)

For ˙m

and ˙m

,wecanwrite:

˙m

= ρ

)dx

and ˙m

= ρ

(δ

+δ

)

)dx

. (13.149)

388 13 Incompressible Fluid Flows

By integration one obtains

˙m

= ρ



−

g cos β

2ν



+ C



. (13.150)

˙m

= ρ



−

g cos β

2ν



(δ

+ δ

)

− δ

+ C

+ δ

+ C

(13.151)

In this way, the layer mass ﬂows ˙m

and ˙m

can be determined, when δ

and δ

are given and the properties of the ﬂuids of the coating ﬂuids are

known.

13.10 Two-Phase Plane Channel Flow

In Fig. 13.12, a plane channel ﬂow is sketched which is composed of the ﬂow

of two superimposed non-mixable ﬂuids, i.e. ﬂuids A and B that ﬂow simul-

taneously through a channel formed by two parallel plates. Fluid A forms a

layer of thickness δ

and has density ρ

,viscosityµ

and mass ﬂow ˙m

The ﬂuid that is on top of it has the density ρ

,viscosityµ

and mass ﬂow

˙m

. For both ﬂuids, the following diﬀerential equations for the molecular

momentum transport τ

hold:

dτ

= −

dΠ

and

dτ

= −

dΠ

. (13.152)

With τ

= −µ dU

the velocity ﬁeld results

dΠ

and

dΠ

. (13.153)

Integration of (13.152) yields for both ﬂuids

Fig. 13.12 Plane channel ﬂow with two-layered ﬂows; a solution is stated for δ =0