Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

12.7 Normal Compression Shock (Rankine–Hugoniot Equation) 359

00.5

1.0

x - 1

x + 1

Isentropic flow

Rankine-Hugoniot shock

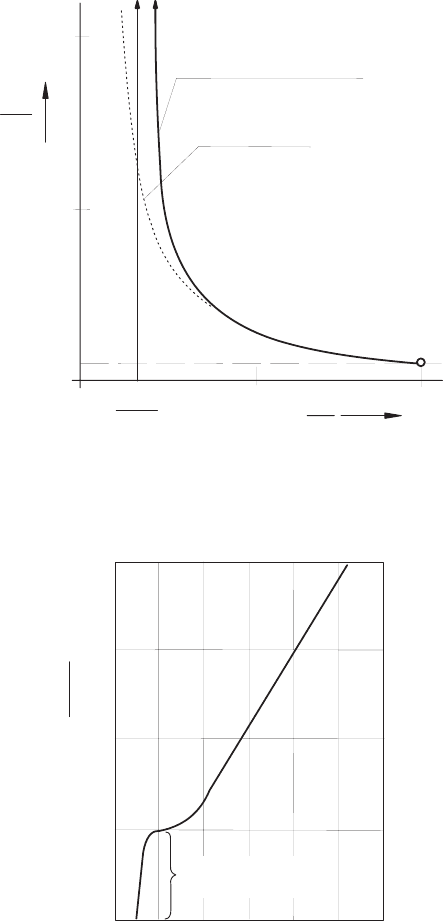
Fig. 12.16 Changes of state for vertical compression shock

1.0 2.0 3.0 4.0 5.0 6.0

3.0

2.0

1.0

-1.0

Normal shocks

are impossible

−

Fig. 12.17 Change of entropy as a result of vertical compression shocks in an ideal

gas with κ =1.4

360 12 Introduction to Gas Dynamics

Figure 12.16 shows further that the ﬂuid is compressed when it is mov-

ing through the compression shock. The pressure, density and temperature

increase on passing through the compression shock, i.e.

≥ 1;

≥ 1; and

≥ 1

When considering the diﬀerence s

− s

, using (12.46), it is evident (see

Fig. 12.17) that s

− s

can only be larger than zero for M

≥ 1. This

expresses that dilution shocks cannot occur in ideal gases, as they are not

permitted by the second law of thermodynamics, which demands s

−s

≥ 0.

In this section only an introduction into gas dynamics was given providing

treatments of compressible ﬂows in a manner also applied in refs. [12.1] and

[12.2] as well as in [12.4] to [12.6]. More advanced treatments are provided in

[12.3].

References

12.1. Boˇsnjakovi´c, F., Technische Thermodynamik I, Verlag von Theodor Steinkopﬀ,

Dresden, Leipzig, 1960.

12.2. Currie, I.G., Fundamental Mechanics of Fluids, McGraw-Hill, New York, 1974.

12.3. Oswatitsch, K., Gasdynamik, Springer, Berlin Heidelberg New York Vienna,

1952.

12.4. Yuan, S.W., Foundations of Fluid Mechanics, Prentice-Hall, Englewood Cliﬀs,

NJ, 1971.

12.5. Becker, E., Technische Thermodynamik, Teubner Studienbuecher, Mechanik,

Stuttgart, 1985.

12.6. Spurk, J.H., Stroemungslehre, Springer, Berlin, Heidelberg, New York, 4. Auﬂ.,

1996.

Chapter 13

Stationary, One-Dimensional Fluid Flows

of Incompressible, Viscous Fluids

13.1 General Considerations

In this chapter, ﬂows of viscous ﬂuids (µ = 0) are considered which are

stationary and two-dimensional. They are assumed to occur in ﬂuids of con-

stant density and, in addition, the ﬂuid is assumed to be fully developed in

the ﬂow direction. The simpliﬁed equations determining this class of ﬂow can

be derived from the general equations of ﬂuid mechanics and the resultant

equations are basically one-dimensional. They are, moreover, for a number of

boundary conditions, accessible to analytical solutions and thus well suited

for students of natural and engineering sciences to provide to them an intro-

duction into ﬂuid mechanics of viscous ﬂuids. The basic knowledge gained

by studying these ﬂuid ﬂows can then be deepened in specialized lectures.

In this way, the knowledge of how ﬂows of viscous ﬂuids behaves in one-

dimensional ﬂow cases can be extended and used for the solution of practical

ﬂow problems.

As shown below, the problems discussed in this chapter can be tackled by

analytical solutions. Hence their properties with regard to the physics of ﬂuid

ﬂows can be described with a few terms of the Navier–Stokes equations and

solutions become possible due to the existence of simple boundary conditions.

In addition, it is assumed that stationarity exists for all ﬂow quantities and

that ﬂuids with a constant density are treated, i.e. ﬂuids with ρ = constant.

This property holds not only for thermodynamically ideal liquids but also,

as shown in Sect. 12.1, for thermodynamically ideal gases when they ﬂow at

moderate velocities.

Simple considerations show that gas ﬂows with Mach numbers Ma ≤ 0.2

can be treated as incompressible with a precision which is suﬃcient for

practical application, i.e. gas ﬂows at low Mach numbers can be treated

as ﬂuids of constant density. For such ﬂuids, the basic equations in the

form stated below hold, for Newtonian media when τ

is introduced as

follows:

361

362 13 Incompressible Fluid Flows

= −µ



∂U

∂x

∂U

∂x



∂U

∂x

  

=0 because

ρ=constant

. (13.1)

• Continuity equation:

∂U

∂x

∂U

∂x

∂U

∂x

=0. (13.2)

• Momentum equations:

– x

-component:



∂U

∂t

+ U

∂U

∂x

+ U

∂U

∂x

+ U

∂U

∂x



= −

∂P

∂x

+ µ



∂

∂x

∂

∂x

∂

∂x



+ ρg

. (13.3)

– x

-component:



∂U

∂t

+ U

∂U

∂x

+ U

∂U

∂x

+ U

∂U

∂x



= −

∂P

∂x

+ µ



∂

∂x

∂

∂x

∂

∂x



+ ρg

. (13.4)

– x

-component:



∂U

∂t

+ U

∂U

∂x

+ U

∂U

∂x

+ U

∂U

∂x



= −

∂P

∂x

+ µ



∂

∂x

∂

∂x

∂

∂x



+ ρg

. (13.5)

13.1.1 Plane Fluid Flows

As a further simpliﬁcation for the subsequent considerations, the ﬂow ﬁeld

is assumed to be two-dimensional, i.e. for all quantities of the velocity and

pressure ﬁelds [∂(···)/∂x

] = 0 can be introduced. It is further assumed that

in the x

direction there is no ﬂow component or that it is always possible

to introduce a coordinate system in such a way that only in the directions

of the two coordinate axes x

and x

do velocity components occur. Thus

one obtains the ﬁnal equations for two-dimensional and two-directional ﬂow

problems, which are employed in the following analytical solutions:

∂U

∂x

∂U

∂x

=0, (13.6)



∂U

∂t

+ U

∂U

∂x

+ U

∂U

∂x



= −

∂P

∂x

+ µ



∂

∂x

∂

∂x



+ ρg

, (13.7)



∂U

∂t

+ U

∂U

∂x

+ U

∂U

∂x



= −

∂P

∂x

+ µ



∂

∂x

∂

∂x



+ ρg

. (13.8)

13.1 General Considerations 363

The above equations are employed in subsequent sections for analytical com-

putations of ﬂuid ﬂows. It is assumed here that the ﬂow causing eﬀects are

known and that they fulﬁl the assumptions made to yield the above-stated

simpliﬁed form of the basic equations, i.e. (13.6)–(13.8).

Further restrictions which are made concerning the subsequently treated

ﬂow problems should be mentioned with regard to the boundary conditions.

It is assumed that these boundary conditions are known and that they fulﬁl

the condition of stationarity, i.e. temporal changes do not occur. Because

of another restriction in the following considerations, only solutions of the

above equations are listed which are laminar. The perturbations acting on

ﬂuid ﬂows in practice constitute, in general, boundary conditions that depend

on time. Moreover, the disturbances have to be considered as unknown. Their

eﬀects on ﬂows are therefore not treated in the subsequent considerations in

this section.

13.1.2 Cylindrical Fluid Flows

For a large number of ﬂow problems, boundary conditions exist which

originate from axi-symmetric ﬂow geometries and which can be introduced

more easily into solutions of the basic equations of ﬂuid mechanics, when

these equations are written in cylindrical coordinates. To provide these

equations, ρ = constant and µ = constant are also assumed.

• Continuity equation:

∂ρ

∂t

+ ρ



∂

∂r

(rU

∂

∂ϕ

∂

∂z

)



=0. (13.9)

• Momentum equations:

– r-component:

∂U

∂t

+ U

∂U

∂r

∂U

∂ϕ

−

+ U

∂U

∂z

= −

∂P

∂r

+ µ



∂

∂r



∂(rU

)

∂r



∂

∂ϕ

−

∂U

∂ϕ

∂

∂z



+ ρg

(13.10)

– ϕ-component:



∂U

∂t

+ U

∂U

∂r

∂U

∂ϕ

+ U

∂U

∂z



= −

∂P

∂ϕ

+µ



∂

∂r



∂(rU

)

∂r



∂

∂ϕ

∂U

∂ϕ

∂

∂z



+ ρg

(13.11)

364 13 Incompressible Fluid Flows

– z-component:



∂U

∂t

+ U

∂U

∂r

∂U

∂ϕ

+ U

∂U

∂z



= −

∂P

∂z

+ µ



∂

∂r



∂U

∂r



∂

∂ϕ

∂

∂z



+ ρg

. (13.12)

For stationary, incompressible (ρ = constant) ﬂuid ﬂows of Newtonian

ﬂuids, assuming axi-symmetry ∂(···)/∂ϕ =0andU

= 0, one can obtain

the following ﬁnal equations:

∂(rU

)

∂r

∂U

∂z

=0, (13.13)



∂U

∂r

+ U

∂U

∂z



= −

∂P

∂r

+ µ



∂

∂r



∂(rU

)

∂r



∂

∂z



+ ρg

, (13.14)



∂U

∂r

+ U

∂U

∂z



= −

∂P

∂z

+ µ



∂

∂r



∂U

∂r



∂

∂z



+ ρg

. (13.15)

These equations can be employed for solutions of ﬂuid ﬂow problems for

stationary axially symmetric ﬂuid ﬂows and for U

=0.

13.2 Derivations of the Basic Equations

for Fully Developed Fluid Flows

13.2.1 Plane Fluid Flows

The basic equations for stationary, two-dimensional and fully developed ﬂuid

ﬂows can be derived from the equations for incompressible Newtonian media

on the assumption that the resulting ﬂuid ﬂow in the x

direction fulﬁls the

following relationships:

∂U

∂x

=0 and

∂U

∂x

=0. (13.16)

Thus the continuity equation is reduced to:

∂U

∂x



∂U

∂x

=0 ;

∂U

∂x

= 0 and therefore U

= f(x

). (13.17)

Based on the assumption of a fully developed ﬂuid ﬂow, the relationships

(13.16) hold and from (13.17) we can derive:

13.2 Derivations of the Basic Equations 365

= constant U



= 0 holds for ﬂuid ﬂows with

impermeable walls



(13.18)

i.e. stationary, incompressible and internal ﬂows are unidirectional. They ﬂow

only in the x

direction, i.e. only one U

component of the ﬂow ﬁeld exists.

This is a statement for the ﬂow ﬁeld that was obtained from the continuity

equation for ﬂuid ﬂows which are fully developed in the ﬂow direction x

.The

momentum equations are simpliﬁed for this class of ﬂuid ﬂows as follows:

direction:

0=−

∂P

∂x

+ µ

∂

∂x

+ ρg

. (13.19)

direction:

0=−

∂P

∂x

+ ρg

. (13.20)

From (13.20), one obtains a general solution for the pressure ﬁeld:

P = ρg

+ Π(x

). (13.21)

The pressure ﬁeld P (x

) comprises an externally imposed pressure, Π(x

which can be applied along the x

axis. The implementation of Π(x

) usually

takes place in practice with pumps and blowers. On introducing this general

pressure relationship into the momentum equation x

,takingU

)into

consideration, one obtains:

0=−

dΠ

+ µ

+ ρg

, (13.22)

i.e. a diﬀerential equation for the unknown ﬂow ﬁeld U

). This is the basic

equation which holds for incompressible, stationary and one-dimensional, i.e.

fully developed, ﬂuid ﬂows, if the ﬂow medium has Newtonian properties and

the ﬂuid can be regarded as incompressible and the viscosity as constant.

Physically, the equation can be interpreted in such a way that the pressure

gradient imposed externally in the x

direction counteracts the viscosity and

mass forces of the ﬂow ﬁeld

dΠ

= µ

+ ρg

. (13.23)

Here it is important that the pressure gradient, in accordance with (13.21),

can assume any externally imposed value, which for the ﬂow problems treated

here must depend only on x

. Considering however, (13.18), and admitting

only constant mass forces, i.e. g

= constant, the right-hand side of (13.22) is

a function only of x

. Thus the pressure gradient in the x

direction assumes

a constant value in the case of stationary, incompressible and one-dimensional

ﬂuid ﬂows.

366 13 Incompressible Fluid Flows

13.2.2 Cylindrical Fluid Flows

Analogous to the above derivations of plane ﬂuid ﬂows, the derivations of

the basic equations for stationary, one-dimensional ﬂuid ﬂows can be made

for axi-symmetric ﬂow cases also. For the following derivation, it is assumed

that in the z direction the ﬂuid ﬂow is fully developed, i.e. all derivatives of

the velocity components are zero in the z direction, as stated below

∂U

∂z

=0,

∂U

∂z

=0. (13.24)

With these assumptions, one obtains from the continuity equation:

∂

∂r

(rU

)=0 ; ρrU

= constant (13.25)

and because of the assumption of impermeable walls for the ﬂuid (see (13.18))

one obtains:



for the presence of impermeable walls

for the considered ﬂuid ﬂow



(13.26)

and thus the momentum equations hold:

0=−

∂P

∂r

+ ρg

. (13.27)

0=−

∂P

∂z

+ µ



∂

∂r



∂U

∂r



+ ρg

(13.28)

by integration of:

P (r, z)=ρg

r + Π(z), i.e.

∂P

∂z

dΠ

. (13.29)

Finally, the above derivations result in:

0=−

dΠ

+ µ



∂

∂r



∂U

∂r



+ ρg

. (13.30)

This last equation represents the conditional equation for the velocity ﬁeld,

which has to be employed for solutions of one-dimensional (fully developed)

ﬂow problems in axi-symmetric geometries.

13.3 Plane Couette Flow

In chemical process engineering, it is common practice, e.g. when coating

sheet metals, foils, plates, etc., to employ coating systems of the kind shown

in Fig. 13.1. This ﬁgure shows that the actual material to be coated is moved

13.3 Plane Couette Flow 367

Outlet chamber

Coated layer

Outlet for

stripped fluid

Prechamber

Substrate to

be coated

Coating fluid

supply

Couette flow

Device to

stripp fluid

Fig. 13.1 Schematic representation of a coating system

through a pre-chamber ﬁlled with the coating ﬂuid. From there the material

enters a channel with plane parallel walls that end in a ﬂuid collecting cham-

ber, where the coating thickness is brought to the required ﬁnal value by

scrubbers installed on both sides. The wiped oﬀ coating material is collected

in the discharge chamber and is fed back through a discharge pipe to the

coating ﬂuid supply system.

The ﬂow forming in the slots between the pre-chamber and the discharge

chamber, after a certain distance from the inlet, is called Couette ﬂow. It is

characterized by the fact that no pressure gradients are used for driving the

ﬂow, i.e. for Couette ﬂow the following holds:

dΠ

= 0 and therefore 0 = µ

+ ρg

. (13.31)

In the case of a horizontal ﬂow direction with respect to the vertical direc-

tion of the ﬁeld of gravity, no mass forces are active which could drive the

ﬂuid ﬂow, as the x

direction is vertical to the direction of the gravitational

acceleration, i.e. for the Couette ﬂow in Fig. 13.1 the following holds:

=0. (13.32)

Thus the basic equation stated in Sect. 13.2 for plane ﬂows is reduced to the

diﬀerential equation describing the Couette ﬂow:

−

dΠ



+ µ

+ ρg



=0 =⇒

∂

∂x

=0. (13.33)

From the resulting equation for U

, i.e. from (13.33), it can be seen that

the velocity proﬁle U

) occurring in the slot is independent of the viscosity

of the coating ﬂuid. Thus also the required quantity of coating material is

independent of the viscosity of the coating medium, a property which is often

regarded to be desirable for well-designed coating systems. The system thus

becomes equally applicable for all ﬂuid properties and results in velocity

proﬁles that are independent of the ﬂuid properties (Fig. 13.2).

368 13 Incompressible Fluid Flows

Velocity profile of

Couette flow

Fig. 13.2 Basic geometry of the upper slit in the coating system shown in Fig. 13.1

(width of the slit in the x

direction is B)

When considering that, for the assumptions made, the velocity U

can

depend on the coordinate x

only, the ﬁnal equation can be written as follows:

=0 ; U

= C

+ C

. (13.34)

Because of the boundary conditions existing due to the operation of the

coating system, the integration constants C

and C

result in values as shown

below

=0:U

= U

= C

0+C

; C

= U

= D : U

=0=C

D + C

; C

= −U

/D.

(13.35)

Thus for the velocity proﬁle one obtains

(D − x

)for0≤ x

≤ D. (13.36)

The required ﬂuid volume of the coating material that has to be supplied

per unit time results from integration over the entire slot having the width

B in the x

direction, i.e. the integration has to be taken over both slot

openings, on the top and at the bottom of the substrate. For the system in

Fig. 13.1,

needed for coating results from the following integration:

Q =2B



−



(13.37)





(13.38)

or as the ﬁnal relationship:

Q =

D. (13.39)