Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows
Подождите немного. Документ загружается.

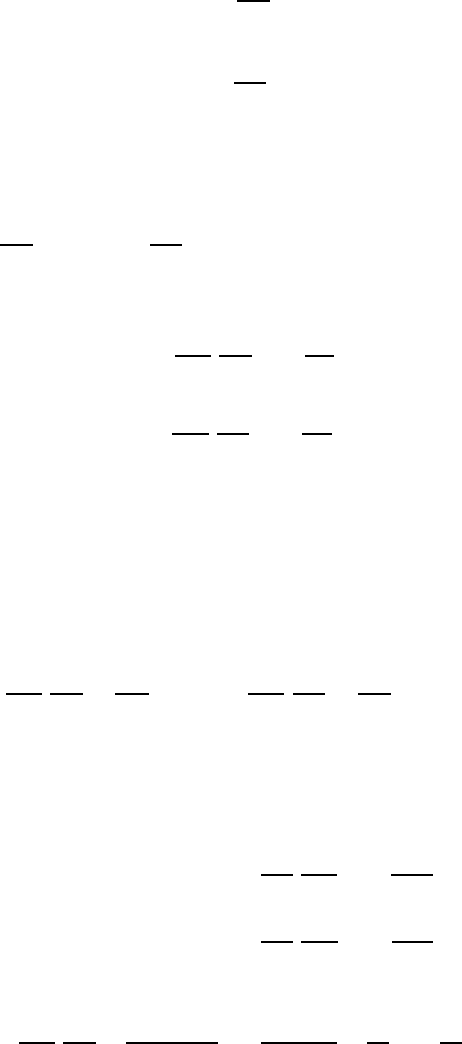
13.10 Two-Phase Plane Channel Flow 389
τ
A
21
= −
dΠ
dx
1
x
2
+ C
A
1
(13.154)
and
τ
B
21
= −
dΠ
dx
1
x
2
+ C
B
1
. (13.155)
Introducing the boundary conditions that the momentum transport is
equal due to the common surface A and B,oneobtainsτ
A
21
(x
2
= δ)=
τ
B
21
(x
2
= δ):
−
dΠ
dx
1
δ + C
A
1
= −
dΠ
dx
1
δ + C
B
1
; C
A
1
= C
B
1
= C
1
. (13.156)
When carrying out the integration for the velocity fields U
A
1
and U
B
1
,one
obtains:
U
A
1
= −
1
2µ
A
dΠ
dx
1
x
2
2
+
C
A
1
µ
A
x
2
+ C
A
2
(13.157)
and
U
B
1
= −
1
2µ
B
dΠ
dx
1
x
2
2
+
C
B
1
µ
B
x
2
+ C
B
2
. (13.158)
The coordinate system plotted in Fig. 13.12 was chosen such that the x
2
direction yields positive values for δ, i.e. the area between the two fluids lies
above the plane x
2
= 0. In this way, one can obtain the second boundary
condition that has to be imposed in the interface
U
A
1
=(x
2
= δ)=U
B
1
(x
2
= δ) ; C
A
2
= C
B
2
, (13.159)
i.e. the following relationship holds:
−
δ
2
2µ
A
dΠ
dx
1
+
C
1
δ
µ
A
+ C
A
2
= −
δ
2
2µ
B
dΠ
dx
1
+
C
1
δ
µ
B
+ C
B
2
, (13.160)
δ = 0 results in a reduction in the effort for determining C
A
2
and C
B
2
.This
special case is discussed below. For δ = 0 it results that C
A
2
= C
B
2
= C
2
.
The remaining integration constants can be determined with the following
boundary conditions:
x
2
= −D ; U
A
1
=0: 0=−
dΠ
dx
1
1
2µ
A
D
2
−
C
1
D
µ
A
+ C
2
, (13.161)
x
2
=+D ; U
B
1
=0: 0=−
dΠ
dx
1
1
2µ
B
D
2
+
C
1
D
µ
B
+ C
2
. (13.162)
Hence one obtains for the velocity distributions in the fluids A and B:
U
A
1
= −
D
2
2µ
A
dΠ
dx
1
+
2µ
A
(µ
A
+ µ
B
)
+
µ
A
− µ
B
µ
A
+ µ
B
x
2
D
−
x
2
D
2
(13.163)
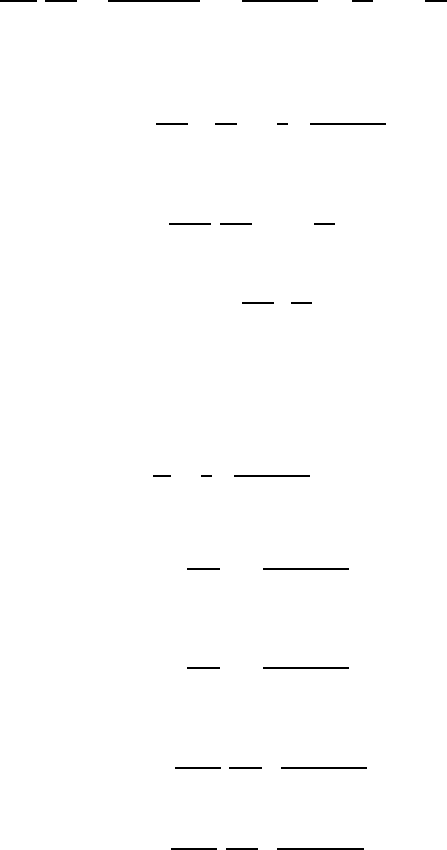
390 13 Incompressible Fluid Flows
and
U
B
1
= −
D
2
2µ
B
dΠ
dx
1
+
2µ
B
(µ
A
+ µ
B
)
+
µ
A
− µ
B
µ
A
+ µ
B
x
2
D
−
x
2
D
2
. (13.164)
For the distribution of the molecular-dependent momentum transport, the
following expression can be deduced:
τ
21
= −D
dΠ
dx
1
x
2
D
−
1
2
µ
A
− µ
B
µ
A
+ µ
B
. (13.165)
When choosing in the above relations µ
A
= µ
B
,oneobtains:
U
1
=
−D
2
2µ
A
dΠ
dx
1
1 −
x
2
D
2
(13.166)
and
τ
21
= −D
dΠ
dx
1
x
2
D
, (13.167)
which ends up in a parabolic velocity profile with the velocity maximum in
the middle of the channel and a linear τ
21
distribution with τ
21
=0onthe
channel axis.
For µ
A
= µ
B
, the position of the velocity maximum, with τ
21
=0,results
from (13.163):
δ
D
=
1
2
µ
A
− µ
B
µ
A
+ µ
B
. (13.168)
The momentum transport to the upper wall yields:
τ
A
W
= −
dΠ
dx
1
D
µ
A
+3µ
B
µ
A
+ µ
B
. (13.169)
The momentum transport to the lower wall yields:
τ
B
W
= −
dΠ
dx
1
D
3µ
A
+ µ
B
µ
A
+ µ
B
. (13.170)
The mean velocities of the partial flows A and B can be computed as:
˜
U
A
1
= −
D
2
12µ
A
dΠ
dx
1
7µ
A
+ µ
B
µ
A
+ µ
B
(13.171)
and
˜
U
B
1
= −
D
2
12µ
B
dΠ
dx
1
µ
A
+7µ
B
µ
A
+ µ
B
. (13.172)
The corresponding mass flows can be computed as:
˙m
A
= BD
˜
U
A
1
and also ˙m
B
= BD
˜
U
B
1
. (13.173)
The above treated one-dimensional flow problems are only a few of
those examples available in many text books of fluid mechanics. For further
examples see refs. [13.1] to [13.2].
References 391
References
13.1. Bird, R.B., Stuart, W.E., Lightfoot, E.N., “Transport Phenomena”, Wiley, New
York, 1960
13.2. Hutter, K., “Fluid- und Thermodynamik- eine Einfuehrung”, Springer, Berlin,
Heidelberg, New York 1995
13.3. Pnoeli, D., Gutfinger, Ch., “Fluid Mechanics”, Cambridge University Press,
Cambridge, 1992
13.4. Potter, M.C., Voss, J.F., “Fluid Mechanics”, Wiley, New York, 1975
13.5. Schlichting, H., “Boundary Layer Theory”, McGraw-Hill, New York, Series in
Mechanical Engineering, 1979
Chapter 14
Time-Dependent, One-Dimensional Flows
of Viscous Fluids
14.1 General Considerations
The flow problems, discussed in Chap. 13 for viscous fluids, were characterized
by the fact, among other things, that they fulfilled the condition of station-
arity, i.e. the examined flows were not dependent on time. All the derivations
in Chap. 13 that led to (13.22), can be repeated, maintaining the time deriva-
tive of the velocity field in the equations. For time-dependent flows, this term
cannot be set equal to zero and, hence, one obtains the basic equation for
time-dependent, one-dimensional flows of viscous fluids, i.e. U
1
= f(x
2
,t):
ρ
∂U
1
∂t
= −
∂Π
∂x
1
+ µ
∂
2
U
1
∂x
2
2
+ ρg
1
(14.1)
where U
1
(x
2
,t)andalsoΠ(x
1
,t) are now to be regarded as functions of
both space and time. On transcribing this equation for incompressible flow,
it follows that:
∂U
1
∂t
= ν
∂
2
U
1
∂x
2
2
time−dependent diffusion
−
1
ρ
∂Π
∂x
1
− g
1
Source term
(14.2)
and one obtains an equation that is well known for dealing theoretically with
transport processes. Without the source term in (14.2), it represents the
fundamental equation for all transient one-dimensional, diffusion problems;
e.g. for unsteady, one-dimensional, heat conduction problems it reads:
∂T
∂t
= α
∂
2
T
∂x
2
2
with α =
λ
ρc
p
(14.3)
Analogous to heat-conduction problems, a number of transient, one-
dimensional flow problems can be solved via analytical methods. For this pur-
pose, it is useful to consider first the dimensionless form of (14.2) without the
393

394 14 Time-Dependent Flows
source term, i.e. the following equation which holds for the one-dimensional
molecular momentum transport:
∂U
1
∂t
= ν
∂
2
U
1
∂x
2
2
⇒
∂U
∗
1
∂t
∗
=
ν
c
t
c
!
2
c
ν
∗
∂
2
U
∗
1
∂x
∗
2
2
(14.4)
In this equation, the term (ν
c
t
c
)/!
2
c
is the reciprocal of the product of the
characteristic Reynolds and Strouhal numbers, Re =(!
c
U
c
)/ν
c
and St =
!
c
/(U
c
t
c
). It may be compared with the Fourier number of heat conduction,
Fo =(a
c
t
c
/!
2
c
), which is normally introduced when dealing, in general, with
time-dependent heat-conduction problems.
For the time-dependent, one-dimensional flow problems of viscous fluids,
to be discussed in this chapter, a generalization of the considerations can be
attained by setting
Fo =
1
ReSt
=
ν
c
t
c
!
2
c
= 1 (14.5)
such that the left- and right-hand sides of (14.4), in the dimensionless form,
are of equal order of magnitude. Hence we are introducing the characteristic
measures of time, length and velocity for purely diffusive flow problems as
follows:
t
c
=
!
2
c
ν
c
!
c
=
√
ν
c
t
c
u
c
=
ν
c
!
c
(14.6)
If a flow is generated in a fluid, with a constant flow velocity U
0
, describing
a one-dimensional problem, its properties can be derived from (14.4) by the
following solution ansatz:
U
1
U
0
= F
x
2
2
√
νt
= F (η)withη =
x
2
2
√
νt
(14.7)
Introducing into (14.4) all terms of (14.7), one can carry out the follow
derivations:
∂U
1
∂t
= U
0
dF
dη
∂η
∂t
= U
0
dF
dη
∂
∂
−
η
2t
= −U
0
η
2t
F
η
(14.8)
∂U
1
∂x
2
= U
0
dF
dη
∂η
∂x
2
= U
0
dF
dη
1
2
√
νt
(14.9)
∂
2
U
1
∂x
2
2
= U
0
∂
∂x
2
dF
dη
∂η
∂x
2
= U
0
3
d
2
F
dη
2
2
∂η
∂x
2
2
+
dF
dη
∂
2
η
∂x
2
2
4
(14.10)
∂
2
U
1
∂x
2
2
= U
0
d
2
F
dη
2
1
4νt
(14.11)
When the partial derivatives in (14.8) and (14.11) are inserted into the partial
differential equation (14.4), that needs to be solved, one obtains an ordinary
differential equation of second order for the function F (η):
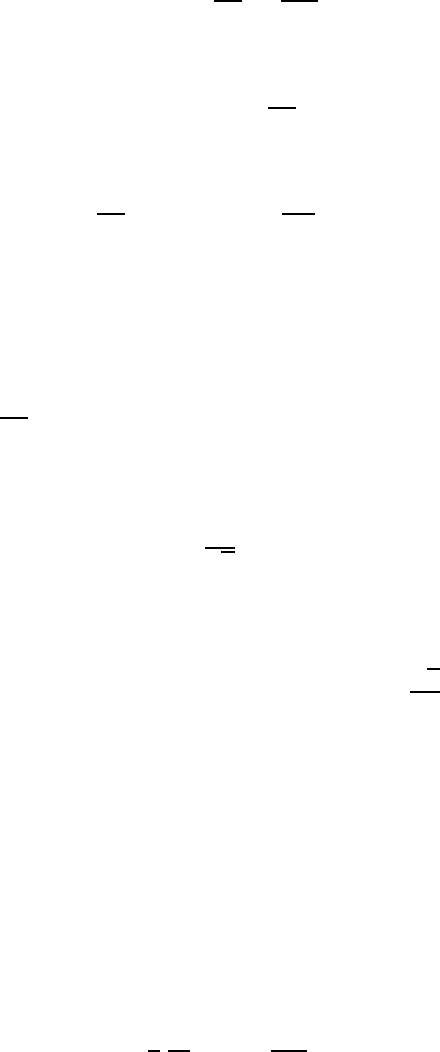
14.1 General Considerations 395
−2η
dF
dη
=
d
2
F
dη
2
(14.12)
By introducing a new function G(η):
G(η)=
dF
dη
(14.13)
one obtains from (14.12):
dG
dη
= −2ηG ⇒
dG
G
= −2η dη (14.14)
Through integration of (14.14), one obtains:
ln G = −η
2
+lnC
1
⇒ G(η)=C
1
exp(−η
2
) (14.15)
Hence one can express the function G(η) as follows:
G(η)=
dF
dη
= C
1
exp(−η
2
) ⇒ F (η)=C
1
η
#
0
exp(−η
2
)dη + C
2
. (14.16)
Using the definition of the error function:
erf(η)=
2
√
π
η
#
0
exp(−η
2
)dη (14.17)
one obtains a general solution for one-dimensional, transient, diffusion-driven
flows of an incompressible fluid:
F (η)=C
1
erf(η)+C
2
with C
1
= C
1
√
π
2
(14.18)
From equation (14.18), one obtains the solution for U
1
:
U
1
= U
0
[C
1
erf (η)+C
2
] (14.19)
In the subsequent sections, the above general solution will be employed in
order to find specific solutions for predefined initial and boundary conditions,
i.e. for different flows.
A number of one-dimensional, unsteady flow problems for incompressible,
viscous fluids can be dealt with more easily in cylindrical coordinates. The
basic equation for such flows can now be stated for such flow problems. The
derivations of the related equations start from the two-dimensional equa-
tions that were derived in Chap. 5 written in cylindrical coordinates. These
equations read:
1
r
∂
∂r
(rU
r
)+
∂U
z
∂z
= 0 (14.20)
396 14 Time-Dependent Flows
ρ
∂U
r
∂t
+ U
r
∂U
r
∂r
+ U
z
∂U
r
∂z
= −
∂P
∂r
+ µ
∂
∂r
1
r
∂ (rU
r
)
∂r
+
∂
2
U
r
∂z
2
+ ρg
r
(14.21)
ρ
∂U
z
∂t
+ U
r
∂U
z
∂r
+ U
z
∂U
z
∂z
= −
∂P
∂z
+ µ
1
r
∂
∂r
r
∂U
z
∂r
+
∂
2
U
z
∂z
2
+ ρg
z
(14.22)
Introducing the demand for the one-dimensionality of the flow, i.e. no change
of the flow field in the z direction because the flow is assumed to be fully
developed:
∂U
r
∂z
=0 and
∂U
z
∂z
= 0 (14.23)
With the help of these expressions, it then follows from the continuity
equation (14.20):
1
r
∂
∂r
(rU
r
)=0 ⇒ rU
r
= F (z,t) (14.24)
Since
∂U
r
∂z
= 0 holds, the function F (z, t)=F (t). Because U
r
=
0 at the wall, the following holds: the one-dimensional, non-stationary flow
of incompressible viscous mediums is unidirectional and has only a U
z
component.
Hence the basic equations in cylindrical coordinates can be reduced to:
0=−
∂P
∂r
+ ρg
r
(14.25)
ρ
∂U
z
∂t
= −
∂P
∂z
+ µ
1
r
∂
∂r
r
∂U
z
∂r
+ ρg
z
(14.26)
By integration of (14.25), one obtains:
P = ρg
r
r + Π(z,t) (14.27)
Thus the equation corresponding to the partial differential equation (14.1),
but written in cylindrical coordinates, reads as follows:
∂U
z
∂t
= ν
1
r
∂
∂r
r
∂U
z
∂r
−
1
ρ
∂Π
∂z
− g
z
(14.28)
This generally valid equation will also be employed subsequently to deal
with unsteady, one-dimensional flows of incompressible, viscous fluids that
are axisymmetric.
14.2 Accelerated and Decelerated Fluid Flows 397
14.2 Accelerated and Decelerated Fluid Flows
14.2.1 Stokes First Problem
Stokes (1851) was one of the first scientists who provided an analytical solu-
tion for an unsteady, one-dimensional flow problem, namely the solution for
the fluid motion induced by the sudden movement of a plate and the related
momentum diffusion into an infinitely extended fluid lying above the plate.
In order to understand better the induced fluid movement, also observed
in practice, in this and the subsequent sections flow processes are discussed
which occur in fluids due to imposed wall movements. The simplest examples
on the subject discussed in this chapter on wall-induced fluid motions concern
the movement of plane plates. However, the general physical insights gained
from these examples are not limited to the plate-induced fluid motions only,
but can also be transferred to axially symmetrical flows (rotating cylinders).
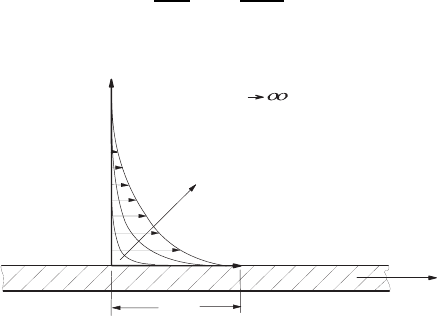
Figure 14.1 shows schematically the velocity distribution which takes place
in a fluid due to a wall moved at a velocity U
0
. The flow setting in, due to
the movement of the plate, can be expressed mathematically as follows:
For t<0:U
1
(x
2
,t)=0
For t ≥ 0:U
1
(x
2
=0,t)=U
0
U
1
(x
2
→∞,t)=0
(14.29)
As a consequence of the fluid viscosity (molecular momentum transport), the
momentum of the fluid layer, moved in the immediate vincinity of the plate,
is transferred to the layers that are further away. With progress of time, layers
that are further away from the moved wall are also included in the induced
fluid motion. The differential equation describing this entire process reads:
∂U
1
∂t
= ν
∂
2
U
1
∂x
2
2
(14.30)
Increase in time
t
U
0
x
2
x
1
U
0
For
x
2
no
fluid motion
Fig. 14.1 Sketch of the flow induced by a plane wall suddenly set in motion

398 14 Time-Dependent Flows
For this equation, the following general solution was found in Sect. 14.1 in
terms of transformed variables, η =
x
2
2
√
νt
and
U
1
U
0
= F (η):
U
1
= U
0
[C
1
erf (η)+C
2
] (14.31)
For the problem of the induced plate movement, the following boundary
conditions result for 0 <t<∞:
x
2
=0, i.e. η =0 U
1
= U
0
(14.32)
and
x
2
→∞, i.e. η →∞ U
1
= 0 (14.33)
From the general solution (14.31) and for the boundary conditions (14.32)
and (14.33), it follows that:
1=C
1
erf(0) + C
2
= C
2
(14.34)
0=C
1
erf(∞)+C
2
= C
1
+ C
2
(14.35)
i.e. the integration constants can be evaluated as:
C
1
= −1andC
2
= +1 (14.36)
Hence the solution reads:
U
1
= U
0
[1 − erf (η)] = U
0
1 − erf
x
2
2
√
νt
(14.37)
This relationship shows that the movement of the plate is imposed on the
fluid only with progressing time. If ν = 0, then for all t and all x
2
,U
1
=0
holds, i.e. without the momentum transport carried out by the molecules,
which is expressed by the finite viscosity of the fluid, one does not succeed
in causing a fluid movement by the movement of the plate. The momentum
in each fluid layer, coming about due to the movement of the plate in the x
1
direction, has to be communicated to the fluid via the molecular momentum
transport. The larger the viscosity ν is, the quicker the fluid layers far away
from the plate are affected, i.e. are set into motion.
For the entire physical understanding of the induced fluid motion, it is
important that the force per unit area acting on the plate can be computed
using:
τ
w
= −µ
∂U
1
∂x
2
x
2
=0
(14.38)
∂U
1
∂x
2
can be evaluated from (14.37):
∂U
1
∂x
2
= U
0
dF (η)
dη
∂η
∂x
2
= −
U
0
√
πνt
exp(−η
2
) (14.39)

14.2 Accelerated and Decelerated Fluid Flows 399
Thus for η = 0 one obtains
∂U
1
∂x
2
x
2
=0
= −
U
0
√
πνt
and consequently:
τ
w
= U
0
0
ρµ
πt
(14.40)
This relationship explains that the required force increases with increase in
viscosity and density of the fluid, to be set in motion, and it decreases with
progress of time. At time t = 0 an infinitely large force results from the
derivations. However, because of the similarity relationship:
η =
x
2
2
√
νt
(14.41)
in which the time appears in the denominator, the result for t = 0 is un-
defined. Consequently, the above statement regarding the required infinitely
large shear force is not permissible. For t →∞one can compute τ
w
→ 0and
U
1
= U
0
for all x
2
, i.e. the entire fluid mass will move with the velocity of
the plate if the plate motion is maintained for a long time.
14.2.2 Diffusion of a Vortex Layer
The so-called first problem of Stokes, discussed in Sect. 14.2.1, can also be
dealt with by means of the vorticity equation which, for the component ω
3
,
can be written as follows:
∂ω
3
∂t
+ U
1
∂ω
3
∂x
1
+ U
2
∂ω
3
∂x
2
= ν
∂
2
ω
3
∂x
1
2
+
∂
2
ω
3
∂x
2
2
(14.42)
With ω
3
= ω and U
2
=0andalso
∂ω
3
∂x
1
=0,oneobtains:
∂ω
∂t
= ν
∂
2
ω
∂x
2
2
(14.43)
This equation describes how the vorticity, continuously produced at the plate
due to its movement, is transported by molecular diffusion into the fluid above
the plate. ω can be expressed in the following way:
ω = −
∂U
1
∂x
2
(14.44)
Thus, the characteristic vorticity for this flow problem can be given as ω
c
=
U
c
/!
c
= U
0
(νt)
1/2
,sothatforω the following similarity approach holds:
ω(η, t)=U
0
(νt)
−1/2
f(η)withη =
x
2
√
νt
(14.45)
