Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

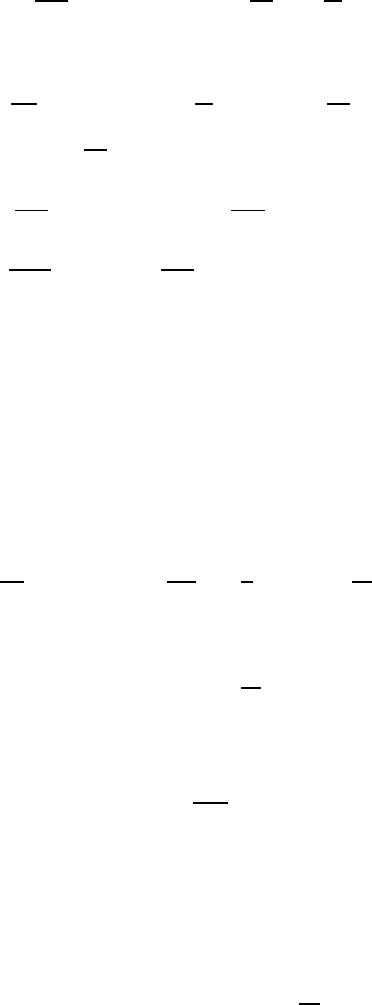
400 14 Time-Dependent Flows

The partial derivatives of η with respect to x

and t are given as:

∂η

∂x

=(νt)

−1/2

and

∂η

∂t

= −

(14.46)

Therefore, one obtains

∂ω

∂t

= U

(νt)

−1/2



−

f(η)+f



(η)

∂η

∂t



= −

(νt)

−1/2

[f(η)+ηf



(η)]

(14.47)

∂ω

∂x

= U

(νt)

−1/2



(η)

∂η

∂x

= U



(η) (14.48)

∂

∂x

= U



(η)

∂η

∂x

= U

(νt)

−1/2



(η) (14.49)

Introducing the equations (14.47) to (14.49) into the partial diﬀerential equa-

tion (14.43), one obtains the following ordinary diﬀerential equation for

f(η):



+ ηf



+ f =2f



+(ηf)



= 0 (14.50)

By integrating this equation once, one obtains:



+ ηf = C

(14.51)

The distribution of the vorticity is symmetrical with respect to x

, and thus



(η =0)=0holdsC

= 0. With this, (14.51) can be rewritten as follows:

dη

= −ηf ;

= −

dη = − d





(14.52)

Therefore, as a solution of this ordinary diﬀerential one obtains:

f(η)=C exp



−



(14.53)

With the following integration:

∞

ω dx

= −

∞

∂U

∂x

= U

(14.54)

and setting ω into the above integral, one obtains

C =(π)

−1/2

(14.55)

Thus as a solution for ω one obtains

ω(x

,t)=U

(πνt)

−1/2

exp



−

νt



(14.56)

14.2 Accelerated and Decelerated Fluid Flows 401

∗

(a) Vorticity

(

Ω

)(

)

∗

1/2

(b) Velocity

(

u/U

)

∗

x = x

(

)

∗

-1/2

Fig. 14.2 Diﬀusion of vorticity and molecular momentum transport in the ﬂuid as

a consequence of a moved plane plate

This solution corresponds to:

,t)=U



1 − erf



√

νt



= U

erfc



√

νt



(14.57)

The diﬀusion of the vorticity, expressed by (14.56) is sketched in a normalized

form in Fig. 14.2 and the corresponding dimensionless velocity distribution

expressed by (14.57) is plotted next to it.

For the ﬂow shown in Fig. 14.2, the following integral parameters can be

computed:

• Vorticity diﬀusion radius

Ω

max

=(πνt)

1/2

(14.58)

• Displacement thickness of the ﬂow

∞

− U

)dx



νt



1/2

(14.59)

• Momentum-loss thickness of the ﬂow

+∞

−∞

− U



νt

8π



1/2

(14.60)

402 14 Time-Dependent Flows

These ﬁnal properties of the ﬂow are usually employed to calculate the state

of the ﬂow at a certain time.

14.2.3 Channel Flow Induced by Movements of Plates

In this section, a one-dimensional transient ﬂow problem of an incompressible

ﬂuid will be discussed, which cannot be solved with the help of the general

solution derived in Sect. 14.1, as this solution is unable to fulﬁl the bound-

ary conditions characterizing the ﬂow problem sketched in Fig. 14.3. This

fact requires the derivation of another particular solution for the diﬀerential

equation characterizing the problem. It is additionally required that the new

solution can satisfy the predeﬁned boundary conditions for the problem un-

der consideration. For this purpose, a solution path is taken which can be

obtained through the well-known Fourier analysis, as employed in the theory

of heat conduction. The ﬂow problem discussed in this section will therefore

serve as an example to point out the application of this known method of

heat conduction in ﬂuid mechanics.

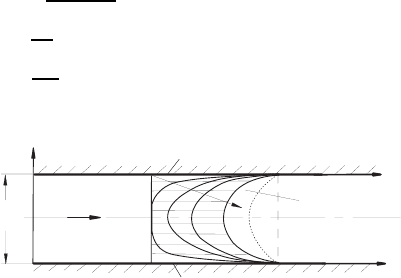
Figure 14.3 shows schematically the ﬂow problem to be solved. Two walls

are shown that are placed in a ﬂuid. Both walls together form a plane channel

between themselves. For t<0 both walls are at rest, whereas they both

assume a velocity U

along the x

-axis for t ≥ 0. As a consequence of this,

a ﬂuid movement is induced, which starts at both sides of the plates and

it moves inwards due to the ﬂuid viscosity. For the problem treated in this

section, the ﬂuid ﬂow induced between the plates and its transient progress

will be discussed.

In order to obtain the solution of the general ﬂow problem of plate-induced

channel ﬂow, the introduction of the following dimensionless quantities is

recommended:

∗

− U

dimensionless velocity

η =

dimensionless position coordinate

τ =

νt

dimensionless time

Induced fluid

Plane plate 1

Plane plate 2

Fig. 14.3 Fluid ﬂow induced by the movement of the walls of a plane channel

14.2 Accelerated and Decelerated Fluid Flows 403

The partial diﬀerential equation:

∂U

∂t

= ν

∂

∂x

(14.61)

describing the ﬂow problem can thus be written:

−

νU

∂U

∗

∂τ

= −ν

∂

∗

∂η

∂U

∗

∂τ

∂

∗

∂η

(14.62)

The initial condition expressed in dimensionless quantities:

τ =0,U

∗

(η) = 1 (14.63)

and the boundary conditions at the walls:

η = ±1,U

∗

(η = ±1) = 0 (14.64)

and also the demand for symmetry at the center line of the channel:

η =0,

∂U

∗

∂η

= 0 (14.65)

deﬁne the ﬂow problem sketched in Fig. 14.3.

For the solution of the partial diﬀerential equation (14.62), there is a classi-

cal solution path, which is based on the method of separation of the variables,

i.e. the solution is sought with an ansatz of the following form:

∗

(η, τ)=f(η)g(τ) (14.66)

From this, it follows that the left-hand side of (14.62) can be expressed as:

∂U

∗

∂τ

= f

dτ

(14.67)

and for the right-hand side:

∂

∗

∂η

= g

dη

(14.68)

The expressions in (14.67) and (14.68) are inserted into the partial diﬀerential

equation (14.62) to yield:

dτ

dη

= −λ

(14.69)

As the left-hand side of this ordinary diﬀerential equation depends only on

the variable τ and the right-hand side only on the variable η, the equation

404 14 Time-Dependent Flows

can only be fulﬁlled when both sides are set equal to a constant which is

introduced into (14.69) as −λ

The following ordinary diﬀerential equations thus result from (14.69) for

the function g:

dτ

= −λ

g (14.70)

and the equation for f reads:

dη

= −λ

f (14.71)

The general solutions of these diﬀerential equations are obtained by

integrations as:

g = A exp(−λ

τ) (14.72)

f = B(cos λη)+C(sin λη) (14.73)

where A, B and C are integration constants. Applying the symmetry of the

solution, demanded in (14.65) to the above solutions, one obtains C =0,as

the sine function is unable to fulﬁl the requirement of symmetry at η =0.

Applying the second boundary condition (14.64), one obtains:

B(cos λ) = 0 (14.74)

In order to permit now a non-trivial solution of the ﬂow problem, i.e. a solu-

tion that is diﬀerent from zero, it is necessary that B = 0, i.e. the introduced

quantity λ can only assume some speciﬁc values such that (14.74) fulﬁls the

boundary conditions. Thus one obtains:

λ =



n +



π for n =0, ±1, ±2, ±3 ... (14.75)

In this way, the general solution of the problem, which fulﬁls the boundary

conditions of the ﬂow problem, results as:

∗

= A

exp

−



n +



cos



n +



πη



(14.76)

Since the governing diﬀerential equation is linear, one obtains the most

general solution as the sum of the individual solutions stated in (14.76):

∗

∞



n→−∞



exp

−



n +



cos



n +



πη



(14.77)

Considering the symmetry of all n functions around n = 0 in the sum (14.77),

the solution can be written as:

14.2 Accelerated and Decelerated Fluid Flows 405

∗

∞



n=0

exp

−



n +



cos



n +



πη



(14.78)

In this expression, D

= A

+ A

−(n+1)

is an integration constant

which assumes a diﬀerent value for each value of n. These values can be

determined from the initial condition (14.63):

∞



n=0

cos



n +



πη



(14.79)

Multiplying (14.79) by

cos



m +



πη



dη

and integrating both sides from η = −1toη = +1, i.e. carrying out the

following integration:

−1

cos



m +



πη



dη =

∞



n=0

−1

cos



m +



πη



cos



n +



πη



dη

(14.80)

one obtains on the right-hand side for all n-values being always zero, when

m = n.Form = n the integration on both sides yields the following

conditional equation for D

sin

m +

πη

m +

−1

= D

m +

π +

sin

m +

2πη

m +

−1

or D

2(−1)

m +

⇒ D

2(−1)

n +

(14.81)

With this conditional equation for D

one obtains the ﬁnal relation for the

plate induced transient channel ﬂow:

∗

+∞



n=0

(−1)

n +

exp

−



n +



cos



n +



πη



(14.82)

or in terms of the dimensional quantities:

= U

− 2U

∞



n=0

(−1)

n +

exp

−



n +



νt

cos



n +





(14.83)

The above inﬁnite series has the property of converging very quickly when

the dimensionless time (νt/D

) is large. On the other hand, the convergence

is slow when (νt/D

) is small. Considering the derived solution (14.83) for

(νt/D

) → 0, the result is in agreement with the solution of the plate-induced

406 14 Time-Dependent Flows

Fig. 14.4 Computed velocity distribution in the ﬂow as a function of location and

time

ﬂuid movement treated in Sect. 4.3.2. By employing Laplace transformation

for small dimensionless times, the employment of (14.37) can be recom-

mended for the computation of the velocity distribution in the channel. This

relationship has to be applied to both halves of the channel and the diﬀerent

positions of the coordinate systems in Figs. 14.1 and 14.3 have to be taken

into consideration.

In Fig. 14.4, a graphical representation is given for the velocity distribution

described by the ﬁnal equation (14.83). This representation shows that, for

small dimensionless times (νt/D

), only the ﬂuid layers between the plane

plates of Fig. 14.3 near the wall are moved. Likewise, only for a dimensionless

time (νt/D

) ≥ 0.04 is a perceivable movement of the ﬂuid in the middle of

the channel obtained. For (νt/D

) ≥ 1, almost the entire ﬂuid in the space

between the plates has reached the plate velocity U

.For(νt/D

) →∞,the

entire ﬂuid moves between the plates with the velocity U

On considering the ﬁnal state of the plate-induced channel ﬂow for

(νt/D

) →∞, one recognizes that it no longer depends on time, i.e. one

should be able to compute it also by solving the partial diﬀerential equation

for stationary, one-dimensional ﬂows. The partial equation and its solution

read

∂

∂x

=0 ⇒ U

= C

+ C

(14.84)

Applying the boundary conditions U

= U

for x

= ±D to this solution,

one obtains

=0 and C

= U

(14.85)

and thus U

= U

is obtained for plane plate-induced channel ﬂow for

(νt/D

) →∞. This solution shows that for the characteristic time of this

14.2 Accelerated and Decelerated Fluid Flows 407

ﬂow problem to go to inﬁnity, all ﬂuid moves at the constant plate velocity;

the entire ﬂuid is swept along by the plates.

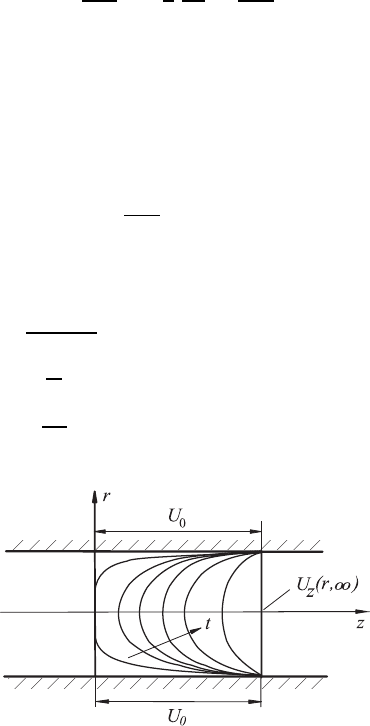
14.2.4 Pipe Flow Induced by the Pipe Wall Motion

Analogous to the ﬂow between two plates discussed in Sect. 14.2.3, which

was caused by the movement of the plate walls, the pipe ﬂow can also be

treated, which is brought about by the movement of the pipe wall as sketched

in Fig. 14.5. The basic equation to this problem is the partial diﬀerential

equation derived from (14.28) where only the ﬁrst term on the right-hand

side is considered:

∂U

∂t

= ν

∂

∂r



∂U

∂r



(14.86)

The ﬂow problem to be studied with this equation can be deﬁned by the

following initial and boundary conditions:

initial condition U

(r, t =0)=0 for0≤ r ≤ R (14.87)

boundary condition U

(R, t)=U

moving wall

for all times t ≥ 0 (14.88)

∂U

∂r

(0,t) = 0 symmetry (14.89)

Analogous to the treatment of the channel ﬂow, induced by the movements

of the walls, the following dimensionless quantities are introduced:

∗

− U

dimensionless velocity (14.90)

η =

dimensionless position coordinates (14.91)

τ =

νt

dimensionless time (14.92)

Fig. 14.5 Fluid ﬂow in a pipe induced by the motion of the pipe walls

408 14 Time-Dependent Flows

Thus the diﬀerential equation (14.86) can be written in dimensionless

quantities as follows:

−ν

∂U

∗

∂τ

= −ν





∂U

∗

∂η

∂

∗

∂η



(14.93)

∂U

∗

∂τ

∂U

∗

∂η

∂

∗

∂η

(14.94)

The following initial condition for the dimensionless velocity results:

τ =0 U

∗

(η) = 1 (14.95)

and boundary conditions can be given for all times t ≥ 0 as follows:

η =1 U

∗

= 0 (14.96)

and

η =0

∂U

∗

∂η

= 0 (14.97)

Again, the classical solution path can be chosen with the ansatz that the

variables can be separated:

∗

(η, τ)=f(η)g(τ) (14.98)

With the substitution of this ansatz into the diﬀerential equation (14.94),

one obtains:

dτ

dη

+ g

dη

(14.99)

As g depends only on τ and f only on η, by separation of variables the

following ordinary diﬀerential equations for g and f result:

dτ

= − λ

(14.100)

dη

= − λ

(14.101)

The solution for the diﬀerential equation (14.100) can be derived by

integration:

g = C

exp(−λ

τ) (14.102)

In order to determine the solution of the diﬀerential equation for f (η),

(14.101) can be written as follows:

dη

+ λ

f = 0 (14.103)

14.2 Accelerated and Decelerated Fluid Flows 409

From rewriting of (14.103), a Bessel diﬀerential equation results:

dη

+ η

dη

+ λ

f = 0 (14.104)

and with

α = λη (14.105)

one obtains

dα

+ α

dα

+ α

f = 0 (14.106)

This equation has the following general solution:

f(α)=C

(α)+C

(α) (14.107)

The solution for J

results from the Bessel diﬀerential equation:



(x)+xy



(x)+(x

− p

)y(x) = 0 (14.108)

which plays an essential role in many ﬁelds of theoretical physics and which

has the solution

(x)=

∞



n=0

(−1)

Γ (n +1)Γ (n + p +1)





2n+p

(14.109)

where the Γ -function is deﬁned as follows:

Γ (n)=

∞

exp (−x) x

n−1

dx for n>0 (14.110)

and can also be determined, for non-discrete values of n,byintegral

arguments.

The function J

(x) is deﬁned as being a Bessel function of the ﬁrst kind

and of order p.

The second function required for the complete solution of the Bessel dif-

ferential equation of zero order (14.106) is the Bessel function of the second

kind, but also of zero order, i.e. Y

(α). This function is often also called the

Neumann or Weber function. Thus the solution ansatz (14.107) in terms of

(α)andY

(α) is composed of the Bessel functions of ﬁrst and second kinds

and of zero order.

Considering the symmetry boundary condition in (14.97) or, noting that

at η =0,Y

(λη) →∞, one ﬁnds C

= 0 in (14.107). Therefore, the solution

for U

∗

, substituting α = λη, may be written as

∗

(η, τ)=C

exp(−λ

τ)J

(λη)=A exp(−λ

τ)J

(λη) (14.111)