Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

12.3 Non-Linear Wave Propagation 339

Momentum equation:

∂U

∂t

+ U

∂U

∂x

= −

∂P

∂x

. (12.26)

From (12.25) the following relation results for ρ = ρ(U):

dρ

∂U

∂t

+ U

dρ

∂U

∂x

+ ρ

∂U

∂x

=0. (12.27)

Analogously, (12.26) can be written:

∂U

∂t

+ U

∂U

∂x



dρ



dρ



∂U

∂x

=0. (12.28)

On multiplying (12.28) by dρ/dU and subtracting it from (12.27), one

obtains:

∂U

∂x



dρ



dρ



∂U

∂x

, (12.29)

or rewriting:

dρ

= ±



dρ



= ±



∂P

∂ρ



. (12.30)

This equation can now be integrated:

dU = ±

∞



dρ



dρ

. (12.31)

For isentropic ﬂows, i.e. P/ρ

= constant, (12.31) can be integrated:

U = ±

∞

√

κ constant ρ

κ−1

dρ

= ±

κ − 1





κρ

κ−1

constant



∞

U = ±

(κ − 1)

(a − c). (12.32)

Thus for the propagation velocity of a wave of large amplitude:

a = c ±

(κ − 1)

U, (12.33)

a propagation velocity a results, which depends on the local ﬂow velocity.

Here c is the computed sound velocity for the undisturbed ﬂuid.

By inserting (12.30) into (12.28), one obtains the following relationship:

∂U

∂t

+ U

∂U

∂x



dρ



∂U

∂x

=0, (12.34)

340 12 Introduction to Gas Dynamics

or rewritten:

∂U

∂t

+(U ± a)

∂U

∂x

=0. (12.35)

From the continuity equation, one obtains:

∂ρ

∂t

+(U ± a)

∂ρ

∂x

=0, (12.36)

so that for ρ the following general solution of the diﬀerential (12.36) can be

stated:

ρ = F

− (U

± a)) = F



−



c ±

κ +1



, (12.37)

where F

() can be any function. Analogously for the velocity:

U = F

(x − (U ± a)) = F



x −



c ±

κ +1



. (12.38)

Equations (12.37) and (12.38) allow one to explain the propagation of a

disturbance with a propagation velocity c ±

κ+1

U. Because of this propaga-

tion velocity, which depends on the local ﬂow velocity, wave deformations

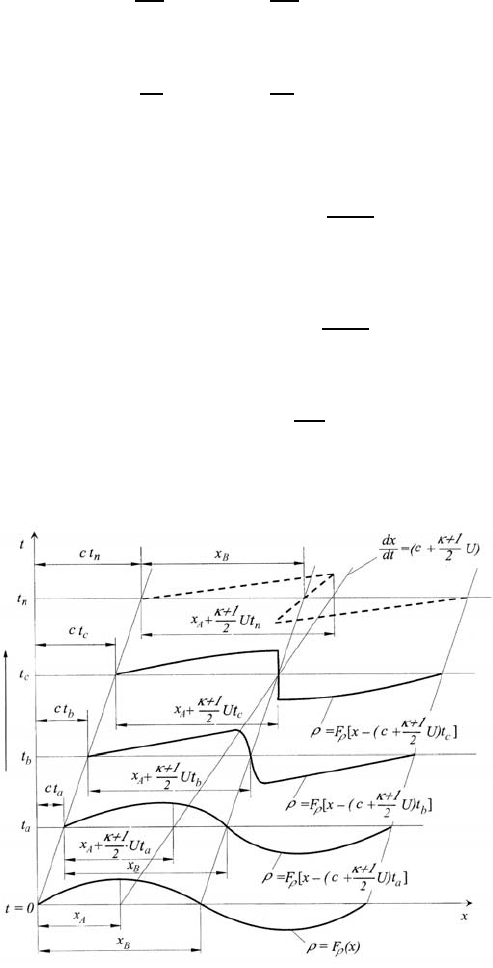
develop as they are indicated in Fig. 12.8. On considering the propagating

Progress in time

Fig. 12.8 Wave deformations and formation of compression shocks

12.4 Alternative Forms of the Bernoulli Equation 341

part with a + sign, then characteristic position changes in times t can be

stated as



= c · t

; x



= x

+ ct

κ +1

; x



= x

+ ct

. (12.39)

The developing and progressive deformation of the wave is apparent. Thus

the formation of compression shocks comes about.

The local ambiguity of the density stated in Fig. 12.8 for t

cannot occur,

of course. When the wave front has built up in such a way that all thermody-

namic quantities of the ﬂuid and also the velocity experience sudden changes,

then the maximum deformation possible of the propagating ﬂow is reached.

A compression shock has built up.

12.4 Alternative Forms of the Bernoulli Equation

In Sect. 9.4.2, the stream tube theory was used to consider one-dimensional

isentropic ﬂows leading to the Bernoulli equation for compressible ﬂows:

(κ − 1)

. (12.40)

The thermodynamically possible maximum velocity was determined for

(P/ρ) → 0:

max

)

2κ

(κ − 1)

2κ

(κ − 1)

. (12.41)

Thus (12.40) may be expressed as

max

−

(κ − 1)

. (12.42)

As the Mach number represents a fundamental quantity in the treatment of

gas-dynamic ﬂow problems, we can write



max



−

2κ

(κ − 1)



max



−

(κ − 1)

. (12.43)

or rewritten:

κ − 1



max



− 1

. (12.44)

The basis for the above considerations was an expanding ﬂow, as it is in-

dicated in Fig. 12.9. For this ﬂow the so-called critical state results, when

the local velocity reaches the speed of sound, i.e. U

= c = U

. Then, from

(12.40):

(κ − 1)

2κ

(κ +1)

. (12.45)

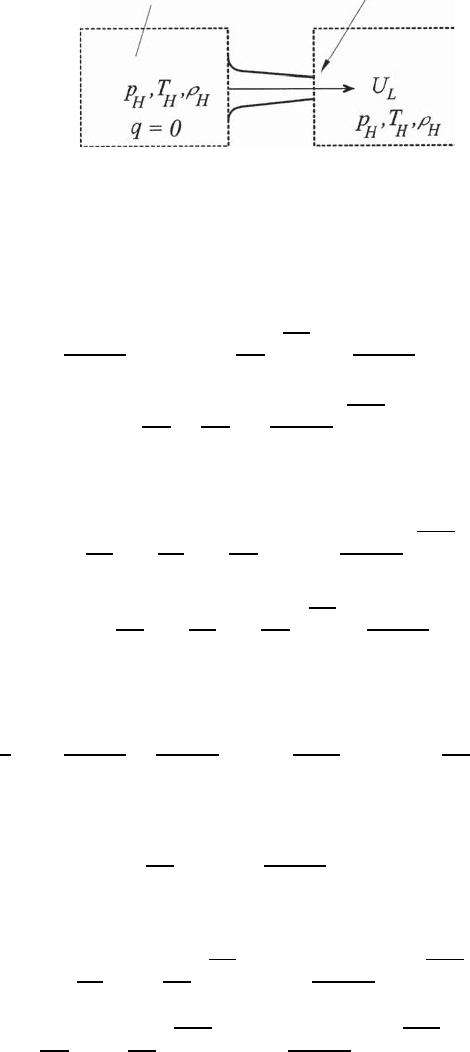
342 12 Introduction to Gas Dynamics

Large reservoir

Nozzle end

x = L

x = 0

Fig. 12.9 Flow between two pressure tanks of diﬀerent pressures

The critical pressure can be computed according to (12.40), considering

(12.45) and assuming isentropy:

2κ

(κ − 1)

1 −





κ−1

2κ

(κ +1)

. (12.46)

∗



(κ +1)



(κ−1)

. (12.47)

Employing the relationships for isentropic density and temperature changes,

one obtains:





∗



∗



1/κ



(κ +1)



(κ−1)

. (12.48)





∗



∗



κ−1

(κ +1)

. (12.49)

The above results may now be expressed in terms of the Mach number. From

Bernoulli’s equation for compressible ﬂuids it follows that:

(κ − 1)

;

κ − 1

+1=

, (12.50)

or rewritten for the temperature ratio:







(κ − 1)



−1

. (12.51)

For the density and pressure variations, the following relations can be

derived:









κ−1



(κ − 1)



−1

(κ−1)

, (12.52)









(κ−1)



(κ − 1)



−κ

(κ−1)

, (12.53)

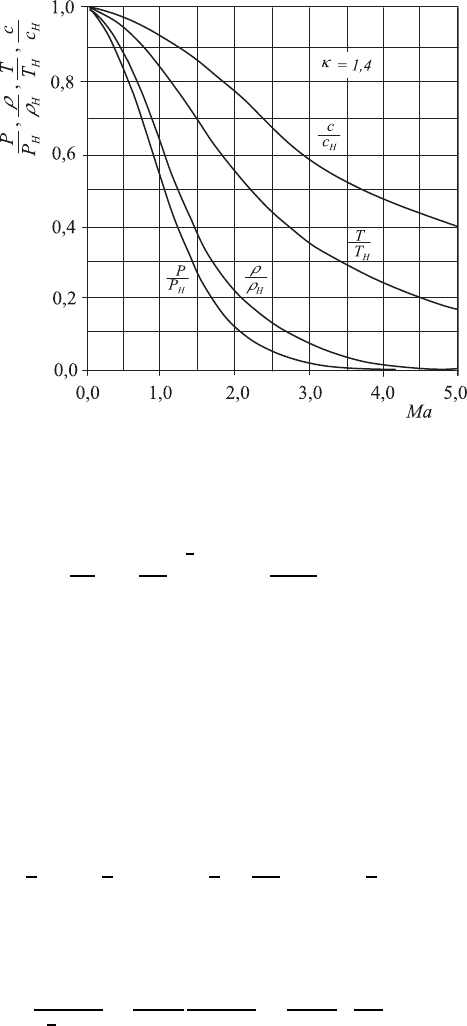
12.4 Alternative Forms of the Bernoulli Equation 343

Fig. 12.10 Diagram representing the parameter variations in the Bernoulli equation

For the sound velocity relation c/c

, the following results:







κ − 1



−2

. (12.54)

The above relationships can be plotted as shown in Fig. 12.10. Thus, as

a result of the Bernoulli equation for isentropic ﬂows, the ﬁgure shows the

change of pressure, density, temperature and speed of sound, each normal-

ized with its stagnation value. All data are represented as functions of Mach

number changes. This ﬁgure corresponds to Fig. 9.10 in Chap. 9, where the

temperature, density and pressure variations with (U

max

) were employed

as a parameter for the representation of diﬀerent forms of the Bernoulli

equation.

It is characteristic for compressible ﬂows that the local dynamic pressure

ρU

ρc



κP



κP Ma

(12.55)

depends on the local pressure and the local Mach number.

For the normalized pressure diﬀerence, the following holds:

− P

ρU

κMa

− P

κMa



− 1



, (12.56)

344 12 Introduction to Gas Dynamics

and with (P

/P ) from (12.53) one obtains:

− P

ρU

κMa



κ − 1



(κ−1)

− 1

. (12.57)

Through a series expansion for Ma

(κ−1)

, the following results:

− P

ρU

=1+

2 − κ

(2 − κ)(3 − 2κ)

192

+··· . (12.58)

For incompressible ﬂows, the Mach number goes to zero so that only the ﬁrst

term of the series expansion remains. For compressible ﬂows, with increasing

Mach number a substantial deviation of C

from the incompressible result is

obtained. However, for Mach numbers below 0.3. this deviation is below 1%.

Therefore, compressibility eﬀects may be neglected up to this Mach number.

This is the basis for treating low-velocity gas ﬂows as incompressible.

12.5 Flow with Heat Transfer (Pipe Flow)

Each chapter in this book tries to give an introduction into a sub-domain

of ﬂuid mechanics and in particular each chapter aims at a deepening of

the physical understanding of the ﬂuid ﬂows treated there. For this purpose,

often simpliﬁcations were introduced into the considerations of an analyt-

ical problem. In the preceding chapter, for example, adiabatic, reversible

(dissipation-free) and one-dimensional ﬂuid ﬂows were treated, i.e. isentropic

ﬂow processes of compressible media which depend on only one space coor-

dinate. These considerations need some supplementary explanation in order

to be able to understand special phenomena in the case of high-speed ﬂows

with heat transfer. For dealing with such ﬂows, which can be considered as

stationary and one-dimensional, i.e. experience changes only in the ﬂow di-

rection x

= x, the following basic equations are available, which are stated

by U

= U:

• Mass conservation:

ρF U =˙m = constant. (12.59)

• Momentum equation:

ρU

= −

. (12.60)

• Energy equation:

(dq)=c

dT + Pd





= c

dT −

dP. (12.61)

12.5 Flow with Heat Transfer (Pipe Flow) 345

• State equation for ideal gases:

= RT. (12.62)

From the mass conservation (12.59), one obtains:

dρ

=0. (12.63)

or for pipe ﬂows with

=0:

= −

dρ

. (12.64)

From the ideal gas (12.62), it can be derived that:

dρ

, (12.65)

and from the momentum equation one obtains −

= U dU or:

−

UdU =

. (12.66)

With κRT = c

and from the momentum (12.66), one obtains:

−

= κMa

. (12.67)

On ﬁnally including the energy equation into the considerations, it can be

stated that the following relationship holds:

(dq)=c

dT −

= c

dT + UdU, (12.68)

or rewritten:

(dq)

−



κRT



(dq)

−

κRT

dT, (12.69)

i.e. for the relative velocity change in a pipe ﬂow as a result of heat supply,

the following can be written:

(κ − 1)Ma



(dq)

−



, (12.70)

346 12 Introduction to Gas Dynamics

where h = c

T was set. From (12.65), it follows that:

−

dρ

= −κMa

, (12.71)

or rewritten:

=(1− κMa

)

. (12.72)

When this relationship is inserted in (12.70), the following results:

(κ − 1)Ma



(dq)

−

1 − κMa



. (12.73)

Solving in terms of

,oneobtains:

(1 − Ma

)

(dq)

. (12.74)

This relationship inserted in (12.64) yields for the relative density change:

dρ

−1

(1 − Ma

)

(dq)

. (12.75)

or for the relative changes in pressure and temperature:

−κMa

(1 − Ma

)

(dq)

and

(1 − κMa

)

(1 − Ma

)

(dq)

. (12.76)

For the local change of the Mach number, it can also be derived that:

d(Ma

)

d(U

)





−

. (12.77)

Thus for the change of the Mach number with heat supply, the following

holds:

dMa

(1 + κMa

)

(1 − Ma

)

(dq)

. (12.78)

As (dq)=T ·ds and h = c

· T it holds furthermore that:

dMa

(1 + κMa

)

(1 − Ma

)

. (12.79)

The above relations can now be employed for understanding how P, T, ρ, U

and Ma change locally when one introduces heat to a pipe ﬂow, i.e. dq/h > 0:

12.5 Flow with Heat Transfer (Pipe Flow) 347

12.5.1 Subsonic Flow

> 0; the ﬂow velocity increases with heat supply.

dρ

< 0and

< 0; density and pressure decrease with heat supply.

> 0; the temperature increases with heat supply for Ma <

< 0; the temperature decreases in spite of heat supply for Ma >

dMa

> 0; the local Mach number increases with heat supply.

The above relationships indicate that, in spite of heat supply, there is

a decrease in temperature for



1/κ < Ma < 1. This is not expected from

simple energy considerations that do not take the above details into account.

12.5.2 Supersonic Flow

< 0; the ﬂow velocity decreases with heat supply.

dρ

> 0and

> 0; density and pressure increase with heat supply.

> 0; the temperature increases with heat supply.

dMa

< 0; the local Mach number decreases with heat transfer.

Thus, in a heated pipe, the change of the thermo-ﬂuid dynamic state diﬀers

substantially, depending on the Mach number of the ﬂow.

If one considers to deepen the physical insight into pipe ﬂows with heat

supply, the processes that occur in the T–s diagram for an ideal gas, one

obtains:

(dq)

= c

= T ds

;



∂T

∂s



, (12.80)

(dq)

= c

= T ds

;



∂T

∂s



, (12.81)

From (12.76), one obtains for the temperature change in a pipe ﬂow with

heat supply:

(1 − κMa

)

(1 − Ma

)

(1 − κMa

)

(1 − Ma

)

T ds

. (12.82)

348 12 Introduction to Gas Dynamics

From this it can be computed that:



∂T

∂s



pipe

(1 − κMa

)

(1 − Ma

)



∂T

∂s



, (12.83)

On now introducing an eﬀective heat capacity c

pipe

= c

, the following

holds:

(dq)

= c

= T ds

;



∂T

∂s



, (12.84)

and c

is computed as:

= c

(1 − Ma

)

(1 − κMa

)

= T



∂T

∂s



. (12.85)

With κ =

,onecanalsowrite:

= c

(1 − Ma

)

− Ma

= T



∂T

∂s



. (12.86)

Hence the following relationship holds:



∂T

∂s



−



∂T

∂s





∂T

∂s



−



∂T

∂s



−

− c

, (12.87)

and further rewritten:





− 1





−



1 − Ma

− 1+κMa

κ − κMa

− 1+κMa

(κ − 1)Ma

(κ − 1)

= Ma

. (12.88)



∂T

∂s



−



∂T

∂s





∂T

∂s



−



∂T

∂s



. (12.89)

In Fig. 12.11, the relationships expressed by (12.89) are shown graphically.

Here (∂T/∂s)

signiﬁes the gradient of the isobars in the T–s state diagram

and (∂T/∂s)

the gradient of the isochors and (∂T/∂s)

the change of the

thermodynamic state of a gas in a pipe ﬂow with heat supply. It can be shown