Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

Chapter 11

Wave Motions in Non-Viscous Fluids

11.1 General Considerations

In Chaps. 9 and 10, ﬂuid ﬂows were considered whose analytical treatment

was possible by employing simpliﬁed forms of the generally valid basic equa-

tions of ﬂuid mechanics. The solution methods required for this are known,

i.e. they are at everybody’s disposal, and it is known that they can be suc-

cessfully employed to solve ﬂow problems. Thus in Chap. 10, for example, the

application of methods was shown which permit the solutions of the basic

equations of ﬂuid mechanics in order to obtain solutions to one- and two-

dimensional ﬂow problems. In particular, in Chap. 10 potential ﬂows were

dealt with whose given properties were chosen such that methods of func-

tional theory can be employed to treat analytically two-dimensional and

irrotational ﬂow problems. Hence, the special properties of potential ﬂows

made it possible to take a fully developed domain of mathematics into ﬂuid

mechanics and to employ it for computing potential ﬂows and their poten-

tial and streamlines. From these computed quantities, velocity ﬁelds of the

treated potential ﬂows could be derived. The employment of the mechanical

energy equation, in its integral form, ﬁnally led to pressure distributions in

the considered ﬂow ﬁelds. The latter again led to the computations of forces

and moments for pre-chosen control volumes. Lift and drag forces were con-

sidered that are of particular interest for the solution of engineering problems.

Simpliﬁcations of the ﬂow properties by introducing two-dimensionality and

irrotationality have thus permitted a closed treatment of ﬂow problems with

known mathematical methods.

A similar solution procedure is adopted in this chapter, in which an in-

troduction to the treatment of wave motions in ﬂuids is attempted. As with

all mechanical wave motions, they are usually treated as ﬂuid motions in a

medium at rest and around a mean location, i.e. the ﬂuid particles involved

in the wave motion experience no change of position when considered over

long times. Thus, in the case of wave motions in ﬂuids, only the energy in the

309

310 11 Wave Motions in Non-Viscous Fluids

Propagation direction of wave

Wave length

Longitudinal wave

Transversal wave

Propagation direction of wave

Compression

Expansion

Compression

Wave len

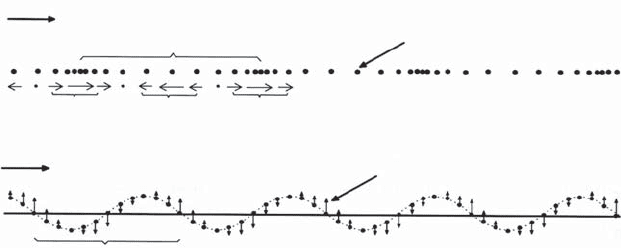
Fig. 11.1 Instantaneous image of progressing longitudinal and transversal waves

wave propagates and not the ﬂuid itself. This holds independently of whether

the wave motions in ﬂuids are longitudinal or transversal waves.

Figure 11.1 shows the oscillation motion of ﬂuid particles for both wave

modes. From the diagrams one can infer that the considered wave motions

are periodical, with regard to both space and time. Oscillations, on the other

hand, are periodical with respect to either time or space.

It can be seen from Fig. 11.1 that mechanical longitudinal waves, which are

characterized by compressions and dilatations i.e. by changes of the speciﬁc

volume or density of a ﬂuid, can exist in all media having “volume elasticity”,

i.e. react with elastic counter forces to the occurring volume changes. Such

counter forces form in gases, and their volume changes are coupled to pressure

changes, so that for an ideal gas at T = constant, the following holds:

P dv = −v dP (11.1)

and therefore, due to compressibility, longitudinal waves can occur in isother-

mal gases, which are not possible in thermodynamically ideal liquids because

of ρ =1/v = constant.

Figure 11.1 also makes it clear that the formation of transversal waves is

dependent on the presence of “shear forces”, i.e. lateral forces must exist in

order to permit the wave motion of “particles” perpendicular to the direction

of propagation. Hence, these mechanical transversal waves only occur in solid

matter which can build up elastic transversal forces. This makes it clear that

in purely viscose ﬂuids no transversal waves are possible. At ﬁrst sight, this

statement seems to be a contradiction to observations of water waves whose

development and propagation can be observed easily when one throws an

object into a water container. A transversal wave develops which, however,

proves to be a wave motion restricting itself to a small height perpendicular

to the water surface. In the interior of the ﬂuid, the wave motion cannot be

observed. Moreover, it can be seen that the observed wave on the surface

does not form due to “shear forces”, but that the presence of gravity or the

occurrence of surface tensions is responsible for the wave motion.

11.1 General Considerations 311

Fig. 11.2 Diagram of a two-dimensional plane wave

in its direction of propagation

In ﬂuids, many diﬀerent wave motions are possible, whose initiation and

existence are connected with an energy input into the ﬂuid. For the generation

of a wave and its maintenance, a certain energy input is necessary which then

propagates in space as the energy of the wave. With this, two diﬀerent types

of energy modes must exist and are essential for a wave to occur. Between

the two types of energy an exchange of energy can take place in a periodical

sequence. This makes it clear that an essential characteristic of a wave motion

in a ﬂuid is that energy is transported without mass transport taking place.

Depending on the form of the wave fronts, i.e. also the form of the source

of the wave motion, one distinguishes diﬀerent wave namely plane waves,

spherical waves and cylindrical waves. For the velocity ﬁeld of such waves the

following can be stated:

Plane waves: u



(x, t)=u

sin



2π



∓



Plane waves (Fig. 11.2) are of particular importance for the considerations

in this chapter. In the case of a plane wave, the mean energy density is

constant, as a considered surface of a wave does not change in area along the

propagation direction x. In the above equation, T is the time of the oscillation

period of the wave motion and λ is the wavelength. The periodicity of the

plane wave in the propagation direction x and the time t can be seen from

the sinusoidal term.

Spherical wave: u



(x, t)=

sin



2π



∓



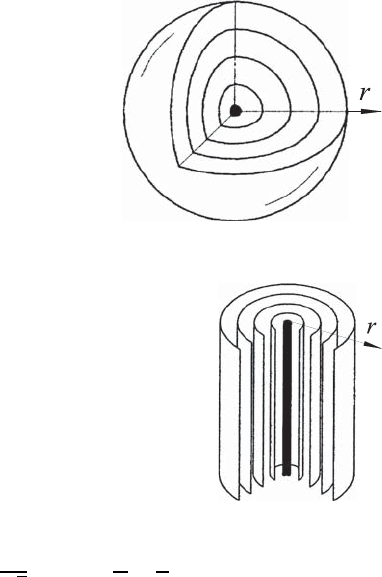
As far as spherical waves in ﬂuids are concerned (Fig. 11.3), the energy

density decreases with the square of the distance from the point r =0,asthe

surface of the sphere increases with the square of the distance. At point r =0

the generator of the spherical wave is located; the entire origin of the energy

of the wave is concentrated at this location. Hence the above equation for a

spherical wave only holds for r = 0. A negative sign in front of the r/λ term

indicates a diverging wave that moves away from the wave centre of origin

and a positive sign indicates a converging wave, moving towards the center

r =0.

312 11 Wave Motions in Non-Viscous Fluids

Fig. 11.3 Diagram of a spherical wave showing

its radial propagation

Fig. 11.4 Diagram of a cylindrical wave showing plane

radical propagation

Cylindrical wave: u



(x, t)=

√

sin



2π



∓



Cylindrical waves (Fig. 11.4) propagate radially from the line of the wave

generation located in the center, i.e. at r = 0. Hence, for cylindrical waves the

wave surface increases linearly with the distance r. Thus the energy density

decreases linearly with the distance r. Therefore, the amplitude of the wave

is inversely proportional to the square root of the distance r from the wave-

generating line. Again, a negative sign in front of the r/λ term indicates a

wave moving from the generating line in the positive r direction, whereas a

positive sign describes a wave moving towards the wave origin.

Many general properties of wave motions, known from physics, can be

transferred to wave propagations in ﬂuids. Nevertheless, in a book meant as

an introduction to ﬂuid mechanics, special considerations are required; in par-

ticular, it is necessary to create a deeper understanding of the causes of the

considered wave motions. Especially it is necessary to show how to deal with

the wave motion on the basis of the Navier–Stokes equations. In the following

sections, important wave motions in ﬂuids are considered. The derivations

of the properties of these waves will show the way in which to proceed in

ﬂuid mechanics to derive the properties from the basic equations of ﬂuid

mechanics. The aim of the derivations is therefore not to provide broad con-

siderations about diﬀerent wave motions in ﬂuids, but an introduction to the

mathematical treatment of longitudinal and transverse waves in ﬂuids.

11.2 Longitudinal Waves: Sound Waves in Gases 313

11.2 Longitudinal Waves: Sound Waves in Gases

In order to be able to deal theoretically with the properties of longitudinal,

e.g. with sound waves, in ideal gases, the basic equations of ﬂuid mechanics

derived in Chap. 5 can be used. These can be stated for ideal gases as follows:

Continuity equation:

∂ρ

∂t

∂(ρU

)

∂x

= 0 (11.2)

Momentum equations: (j =1, 2, 3)



∂U

∂t

+ U

∂U

∂x



= −

∂P

∂x

−

∂τ

∂x

+ ρg

(11.3)

Thermal energy equation:

ρc



∂T

∂t

+ U

∂T

∂x



= −

∂q

∂x

− P

∂U

∂x

− τ

∂U

∂x

(11.4)

State equation:

= RT and e = c

T (11.5)

The above system of partial diﬀerential equations and thermodynamic state

equations comprises seven unknowns, namely U

, U

, P , ρ, e and T ,for

the determination of which, seven equations are available. Thus we have a

closed system of equations which, with suﬃcient initial and boundary condi-

tions, can be solved, at least in principle. It deﬁnitely therefore allows one to

treat ﬂuid motions caused by longitudinal waves.

The above system of equations is considerably simpliﬁed when one neglects

the diﬀusive heat and momentum transport terms, so that all terms of the

momentum and energy equation provided by q

and τ

can be dropped. Mass

forces can also be neglected, i.e. g

= 0. Maintaining the tensor approach, the

equations, after introduction of the suggested simpliﬁcations, can be written

as follows:

Continuity equation:

∂ρ

∂t

∂(ρU

)

∂x

= 0 (11.6)

Momentum equations: (j =1, 2, 3)

= ρ



∂U

∂t

+ U

∂U

∂x



= −

∂P

∂x

(11.7)

Energy equation:

= ρc



∂T

∂t

+ U

∂T

∂x



= −P

∂U

∂x

(11.8)

314 11 Wave Motions in Non-Viscous Fluids

State equation:

= RT and e = c

T (11.9)

Taking into consideration that the continuity equation can be written as

∂ρ

∂t

+ U

∂ρ

∂x

+ ρ

∂U

∂x

Dρ

+ ρ

∂U

∂x

= 0 (11.10)

the following relationship holds:

∂U

∂x

= −

Dρ

. (11.11)

Inserting (11.11) into the energy equation (11.8) and considering the state

equation (11.9), the energy equation can be written in the following form:

ρc





ρR



= P



Dρ



(11.12)

ρc



−

Dρ



Dρ

(11.13)



R + c



Dρ

. (11.14)

Considering R =(c

−c

)andκ =(c

) permits the following relationship

to be derived:

= κ

Dρ

. (11.15)

Equation (11.15) allows the following general solution to be derived by

integration:

(ln P )=

(ln ρ

) (11.16)







=0 ;

= constant. (11.17)

The above relationship shows that the energy equation can be reduced to

the adiabatic equation of property changes known in thermodynamics. This

implies that no molecular heat and momentum transport takes place. The

relationship was derived from the energy equation, taking into account the

continuity equation and the state equation for ideal gases. Thus, along a

stream line of a ﬂow the following relation holds for the indicated conditions

of the considered ﬂuid motion:

= constant. (11.18)

11.2 Longitudinal Waves: Sound Waves in Gases 315

There exist a number of ﬂuid mechanics processes in compressible media

that can be dealt with by means of reduced equations, which result from

the above equations by further simpliﬁcations. Assuming that there are ﬂow

processes that take place in such a way that the velocity ﬁeld depends only

on one spatial coordinate, then we can write U

= U

), U

= U

)and

= U

). Moreover, the simpliﬁcations

∂U

∂x



∂U

∂x

and

∂U

∂x



∂U

∂x

are

introduced so that the following equations can be stated:

Continuity equation:

∂ρ

∂t

∂

∂x

(ρU

) = 0 (11.19)

Momentum equation:



∂U

∂t

+ U

∂U

∂x



= −

∂P

∂x

(11.20)

Energy equation:

= constant (11.21)

By sound waves one understands the propagation of small disturbances

in gases. The sound velocity is, therefore, the velocity with which small dis-

turbances propagate in a ﬂuid at rest. Whereas for an incompressible ﬂuid

an inﬁnitely large propagation velocity results for small disturbances. For

compressible ﬂuids a ﬁnite propagation velocity results, deﬁned by the con-

sidered kind of gas and its temperature. The quantitative determination of

the propagation velocity of small disturbances in ﬂuids at rest can be de-

rived as stated below by employing equations (11.19)–(11.21), which hold for

unsteady, one-dimensional non-viscous, compressible ﬂuids.

Computing the pressure gradient (∂P/∂x

) in (11.20), one obtains:

∂P

∂x



dρ



∂ρ

∂x

. (11.22)

This relationship results since the pressure is a function of only one

thermodynamic quantity, such as the density, as shown by (11.21). The dif-

ferentiation dP/dρ has to be applied for the adiabatic conditions as required

by (11.21). The continuity equation and the momentum equation can thus

be written for one-dimensional ﬂuid ﬂows as:

∂ρ

∂t

+ U

∂ρ

∂x

+ ρ

∂U

∂x

= 0 (11.23)

∂U

∂t

+ U

∂U

∂x



dρ



∂ρ

∂x

=0. (11.24)

316 11 Wave Motions in Non-Viscous Fluids

These two equations are available for the two unknowns U

and ρ,whose

analytical solution is sought on the hypothesis that through the wave motion

small pressure and density ﬂuctuations exist, i.e. the following holds:

=0+u



,t) P = P

+ p



,t) (11.25)

ρ = ρ

+ ρ



,t).

These relationships inserted in the above equations (11.23) and (11.24) lead

to:

∂

∂t

(ρ

+ ρ



)+u



∂

∂x

(ρ

+ ρ



)+(ρ

+ ρ



)

∂u



∂x

= 0 (11.26)

∂u



∂t

+ u



∂u



∂x



dρ



(ρ

+ ρ



)

∂

∂x

(ρ

+ ρ



)=0. (11.27)

On considering that the variables ρ



and u



depend on the location and

time, whereas the quantities P

and ρ

do not depend on either location or

time, the following set of partial diﬀerential equations results. To derive these,

the assumption was introduced that the products of ﬂuctuating quantities are

negligible with reference to the linear terms:

∂ρ



∂t

+ ρ

∂u



∂x

=0 and

∂u



∂t



dρ



∂ρ



∂x

=0. (11.28)

There are now two diﬀerential equations for ρ



and u



that can be employed

to yield solutions for ρ



and u



. In order to obtain the solution for the prop-

agation of sound waves, the ﬁrst of the above two equations is diﬀerentiated

with respect to t:

∂



∂t

+ ρ

∂



∂x

∂t

=0. (11.29)

The second equation multiplied by ρ

and diﬀerentiated with respect to x

yields:

∂



∂x

∂t



dρ



∂



∂x

=0. (11.30)

The subtraction of (11.30) from (11.29) results in a diﬀerential equation

for ρ



∂



∂t

−



dρ





∂



∂x



=0. (11.31)

Furthermore, the diﬀerentiation of (11.28) with respect to x

yields:

∂



∂t∂x

+ ρ

∂



∂x

= 0 (11.32)

11.2 Longitudinal Waves: Sound Waves in Gases 317

and multiplication of (11.28) by ρ/(

dρ

)

and diﬀerentiation with respect to

t leads to:

∂



∂t∂x



dρ



∂



∂t

=0. (11.33)

The subtraction of (11.33) from (11.28) and multiplication by



dρ



results in:

∂



∂t

−



dρ



∂



∂x

= 0 (11.34)

which is the diﬀerential equation for the velocity ﬂuctuation u



By comparing the diﬀerential equations for ρ



and u



, one sees that both

havethesameform,i.e.ρ



and u



willshowthesamedependenceonlocation

and time. The solutions for both quantities are stated by the one-dimensional

wave equation, i.e. there exists a wave motion for ρ



and u



with a propagation

velocity which generally reads:

c =



dρ



κρ

κ−1

√

κRT . (11.35)

The general solutions of the diﬀerential equations for ρ



,t)andu



,t)

can be stated as follows:



= f

−ct)+g

+ ct)andu



= f

−ct)+g

+ ct), (11.36)

where f

ρ,u

− ct) represents the respective wave which propagates in the

positive x

direction and g

ρ,u

+ ct) the wave moving in the negative x

direction.

Further considerations on the propagation of disturbances in compressible

ﬂuids at rest can now be made on the basis of the above results. To this

eﬀect, one computes from the general solution for u



(wave in the positive x

direction):

∂u



∂t

= −c



∂f

∂η



with η = x

− ct (11.37)

and

∂u



∂t

= −c

∂u



∂x

. (11.38)

From the momentum equation it follows that

∂u



∂t

= −

∂ρ



∂x

= −c

∂u



∂x

(11.39)

or rewritten

∂u



∂x

∂ρ



∂x

=⇒



. (11.40)

318 11 Wave Motions in Non-Viscous Fluids

When we have a disturbance in the form of a compression wave, i.e. ρ



> 0,

then also u



> 0, and this means that the ﬂuid particles move in the direction

of the disturbance when a compression disturbance occurs.

When, on the other hand, an expansion disturbance occurs, i.e. ρ



< 0,

then also u



< 0, and in this case the ﬂuid particles move opposite to the

direction of the propagation of the disturbance.

The most important result obtained from the above derivations was that

small disturbances in non-viscous and compressible ﬂuids at rest propagate

with the sound velocity of the ﬂuid that can be computed as follows:

c =



dρ



√

κRT . (11.41)

This relationship will ﬁnd extensive employment in the derivations in

Chap. 12.

11.3 Transversal Waves: Surface Waves

11.3.1 General Solution Approach

On free surfaces of ﬂuids, transversal wave appearances and wave prop-

agations can occur, i.e. propagation of transversal waves introduced by

disturbances. These can be two- or three-dimensional; however, the analytical

treatment of surface waves presented here concentrates on two-dimensional

surface waves. By linearization of the basic equations written in potential

form, one obtains the partial diﬀerential equations, normally solved for sur-

face waves. Looking at these indicates that the treatment of the propagation

of surface waves belongs to the ﬁeld of the potential theory. The treatment

of waves takes place separately, as a special problem, i.e. with surface waves,

a special class of ﬂow problems occurs whose treatment correspondingly re-

quires a special methodology. The latter is shown below in an introductory

way.

The relationships stated in the following can again be derived from the

basic equations of ﬂuid mechanics, which can be stated as follows for a ﬂuid-

mechanically ideal ﬂuid, i.e. a non-viscous ﬂuid:

∂U

∂t

+ U

∂U

∂x

= −

∂P

∂x

+ g

. (11.42)

By integrating this equation over a period of time τ, one obtains

∂U

∂x

dt = −

∂

∂x

P dt +

dt. (11.43)