Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

10.1 Potential and Stream Functions 279

Fig. 10.2 Schematic representation of the ﬂow between ﬂow lines

It holds, however, that dΨ = U

−U

, so that the following can be

written:

Q =

− U

dΨ = Ψ

− Ψ

. (10.12)

It should be mentioned that from the statement that Ψ = constant are

stream lines of the considered ﬂow ﬁeld, it follows immediately that solid

walls have to run tangentially to lines Ψ = constant. From the orthogonality

of equipotential lines and stream lines, which is shown in the following section,

it results at once that equipotential lines always have to stand vertically on

solid walls. When one considers the stream lines of a ﬂow ﬁeld, which can

be given for two-dimensional potential ﬂows in connection with the potential

lines of the same ﬂow ﬁeld, i.e. lines with Φ = constant, one ﬁnds that Ψ =

constant and Φ = constant lines lie orthogonally to one another. This can be

shown by stating the total diﬀerential dΦ:

dΦ =

∂Φ

∂x

∂Φ

∂x

, (10.13)

or writing the same with consideration of (10.3) as follows:

dΦ = U

+ U

. (10.14)

The lines Φ = constant are thus given by:





Φ=constant

= −

. (10.15)

A comparison of relationships (10.10) and (10.15) yields:





= −





. (10.16)

280 10 Potential Flows

As the gradient of the equipotential lines is equal to the negative reciprocal

of the gradient of the ﬂow lines, these lines form an orthogonal net. The

velocity along a stream can be computed as



∂Φ

∂s



Ψ =constant

. (10.17)

This relationship is often used in investigations of ﬂow ﬁelds for which

values of ﬂow lines and equipotential lines have been computed or have to be

obtained from measurements.

From the above derivations, it is apparent that a stream function Ψ can

be computed when the potential function Φ is known and that also inversely

the potential function Φ can be determined when the stream function Ψ is

available. The procedure for determining one function from the other is to

be considered in accordance with the following single steps for determining

the stream function:

• The known potential function Φ(x

) is examined with regard to

whether it represents a solution of (10.5).

• By partial diﬀerentiation of the function Φ(x

) with respect to x

and

the velocity components U

and U

are determined, in accordance with

relations (10.3).

• From this the gradient of the equipotential line can be determined [see

(10.15)]:





= −

• From (10.16) it follows for the gradient of the stream lines that





• By integration of this relationship, the course of the stream lines is

determined. These are lines of constant Ψ values.

10.2 Potential and Complex Functions

The considerations in Sect. 10.1 have shown that the velocities U

and U

can

be stated as partial derivatives of the stream function and the potential func-

tion for irrotational two-dimensional ﬂows of incompressible and viscosity-free

ﬂuids:

∂Φ

∂x

∂Ψ

∂x

, (10.18)

and

∂Φ

∂x

= −

∂Ψ

∂x

. (10.19)

10.2 Potential and Complex Functions 281

On the basis of their deﬁnition, the stream and potential functions satisfy

the Cauchy–Rieman diﬀerential equations:

∂Φ

∂x

∂Ψ

∂x

, (10.20)

∂Φ

∂x

= −

∂Ψ

∂x

. (10.21)

These relationships provide the basis to deduce that a complex analytical

function F (z) (see Sect. 2.11.6) can be introduced in which Φ(x, y)represents

the real part and Ψ (x, y) the imaginary part of the function F(z). The latter

being refered to as the complex potential of the velocity ﬁeld. This function

is usually written as:

F (z)=Φ(x, y)+iΨ(x, y), (10.22)

where x = x

and y = x

and z = x + iy indicates a point in the considered

complex number plane. Conversely, it can be said that for any analytical

function it holds that its real part represents automatically the potential of a

velocity ﬁeld whose stream lines are described by the corresponding imaginary

part of the complex function F (z). As a consequence, it results that each real

part of an analytical function, and also the corresponding imaginary part

of F (z), separately fulﬁl the two-dimensional Laplace equation. Analytical

functions, as they are dealt with in functional theory, can thus be employed

for describing potential ﬂows. When setting their real part (x, y)equalto

the potential function Φ(x, y) and the imaginary part Im(x, y) equal to the

stream function Ψ (x, y), it is possible to state these as the equipotential

and the stream lines. By proceeding in this way, solutions to ﬂow problems

are obtained without partial diﬀerential equations having to be solved. The

inverse way of proceeding, which is sought in this chapter for the solution of

ﬂow problems, namely interpreting a known solution of the potential equation

as a ﬂow, is regarded as acceptable because of the evident advantages of

proceeding in this way for introducing students to the subject of potential

ﬂows.

From a complex potential F (z), a complex velocity can be derived by

diﬀerentiation. As F (z) represents an analytical function, and therefore is

continuous and can be continiously diﬀerentiated. The diﬀerentiation has to

be independent of the direction in which it is carried out, as is shown in the

following. Since the smoothness of F (z) holds, we can derive:

= lim

∆z→0

∆F

∆z

= lim

∆z→0

∆F

(z + ∆z) − z

= lim

∆z→0

∆F

(x + ∆x)+i(y + ∆y) − (x + iy)

282 10 Potential Flows

and as one is free to choose the way in which ∆z goes towards zero (the

diﬀerentiation has to be independent of the approach selected), the following

special ways can be taken into consideration:

∆y =0:

= lim

∆x→0

∆F

(x + ∆x)+iy −(x + iy)

= lim

∆x→0

∆F

∆x

∂F

∂x

∆x =0:

= lim

∆y→0

∆F

x + i(y + ∆y) − (x + iy)

= lim

∆y→0

∆F

i∆y

∂F

i∂y

= −i

∂F

∂y

The result of diﬀerentiation of the complex potential F (z)isthusfor

x = x

w(z)=

dF (z)

∂Φ

∂x

+ i

∂Ψ

∂x

, (10.23)

or, expressed in velocity components:

w(z)=U

− iU

. (10.24)

Based on the above considerations, the following also holds:

w(z)=

dF (z)

∂Φ

i∂x

+ i

∂Ψ

i∂x

, (10.25)

or after transformation, considering that i

= −1, one can write:

w(z)=

∂Ψ

∂x

− i

∂Φ

∂x

= U

− iU

. (10.26)

The above relationships are used in the following to investigate diﬀerent

potential ﬂows. For these investigations, occasionally use is made of the fact

that the complex number z can also be stated in cylindrical coordinates (r, ϕ):

z = re

(iϕ)

= r cos ϕ + ir sin ϕ. (10.27)

Between the velocity components in Cartesian coordinates and in

cylindrical coordinates, the known relationships:

= U

cos ϕ − U

sin ϕ, (10.28)

= U

sin ϕ + U

cos ϕ (10.29)

hold. Thus, for the complex velocity the following expressions result:

w(z)=

dF (z)

= U

− iU

=(U

cos ϕ − U

sin ϕ) − i(U

sin ϕ + U

cos ϕ)

= U

(cos ϕ − i sin ϕ) − iU

(cos ϕ − i sin ϕ), (10.30)

w(z)=(U

− iU

(−iϕ)

. (10.31)

10.3 Uniform Flow 283

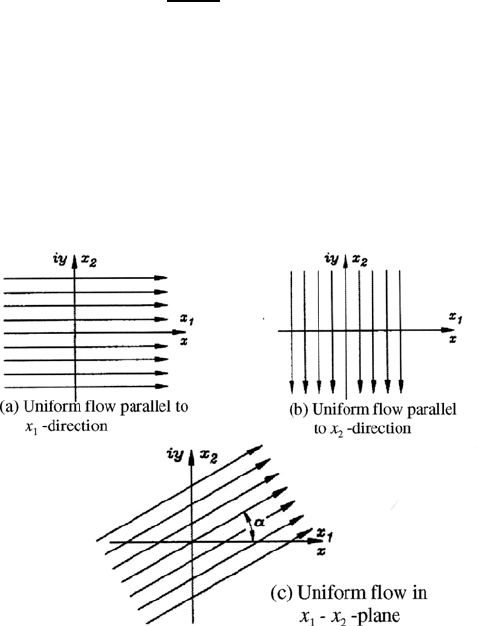
10.3 Uniform Flow

Probably the simplest analytical function F (z), disregarding a constant, is

a function which is directly proportional to z and whose proportionality

constant is a real number:

F (z)=U

z = U

(x + iy). (10.32)

This analytical function describes a ﬂow with the following potential and

stream functions:

Φ(x, y)=U

x and Ψ(x, y)=U

y. (10.33)

Via the relationship for the complex velocity, one obtains:

w(z)=

dF (z)

= U

− iU

, (10.34)

or for U

= U

and U

= 0, the complex potential F (z) describes a uniform

ﬂow parallel to the x

-axis or the x-axis. This ﬂow is sketched in Fig. 10.3a.

For the velocity ﬁeld it can be deduced that in every point of the ﬂow ﬁeld,

the velocity components are U

= U

and U

=0.

This ﬁgure shows the stream lines Ψ = constant, where the arrows in-

dicate the direction of the velocity. The potential lines Φ = constant are

not indicated in Fig. 10.3a. In Fig. 10.3b, stream lines of another ﬂow are

Fig. 10.3 Uniform ﬂow in the (a) x

and (b)thex

direction and (c) in the direction

of the angle α relative to the x

direction

284 10 Potential Flows

shown, representing the lines parallel to the x

-axis. When the proportionality

constant is imaginary, i.e. it holds that:

F (z)=iV

z = V

(−y + ix), (10.35)

then one obtains for the potential and stream functions:

Φ(x, y)=−V

y and Ψ(x, y)=V

x. (10.36)

For the complex velocity it is computed that:

w(z)=iV

= U

− iU

, (10.37)

or U

=0andU

= −V

, i.e. in this case the complex potential describes a

ﬂow parallel to the x

-axis or the y-axis which takes place in the direction of

the negative axis (see Fig. 10.3b).

When there is a ﬂow in the direction indicated in Fig. 10.3c, the complex

potential is:

F (z)=(U

− iV

=(U

− iV

)(x + iy).

(10.38)

From this result, the following relationships for Φ(x, y)andΨ(x, y)canbe

obtained:

Φ(x, y)=U

x + V

y and Ψ (x, y)=U

y −V

Via the complex velocity, one obtains:

w(z)=U

− iV

= U

− iU

. (10.39)

= U

and U

= V

, The components give a velocity ﬁeld which is sketched

in Fig. 10.3c.

10.4 Corner and Sector Flows

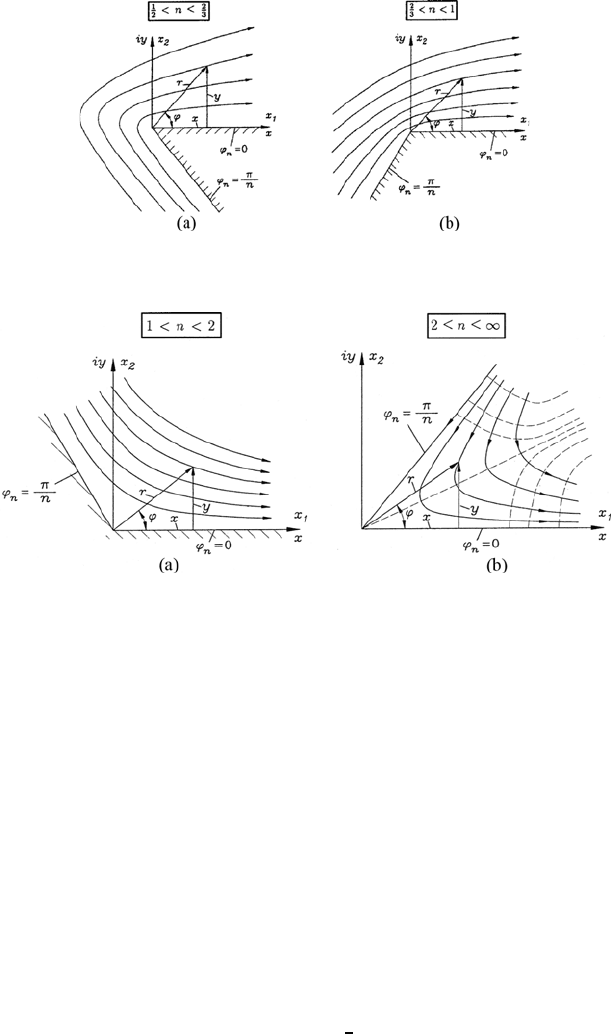
Potential ﬂows around corners and or in sectors of deﬁned angles are described

by a complex potential F (z) which is proportional to z

,whereforn ≤ 1

ﬂows around corners are described, and for n ≥ 1, ﬂows in sectors of angles

are obtained. This will be derived and explained through the following

considerations. The derivations below are based on the following complex

potential:

F (z)=Cz

. (10.40)

When one replaces z by z = re

(iϕ)

and divides the complex potential into

real and imaginary parts, one obtains:

F (z)=C [r

cos(nϕ)+ir

sin(nϕ)]. (10.41)

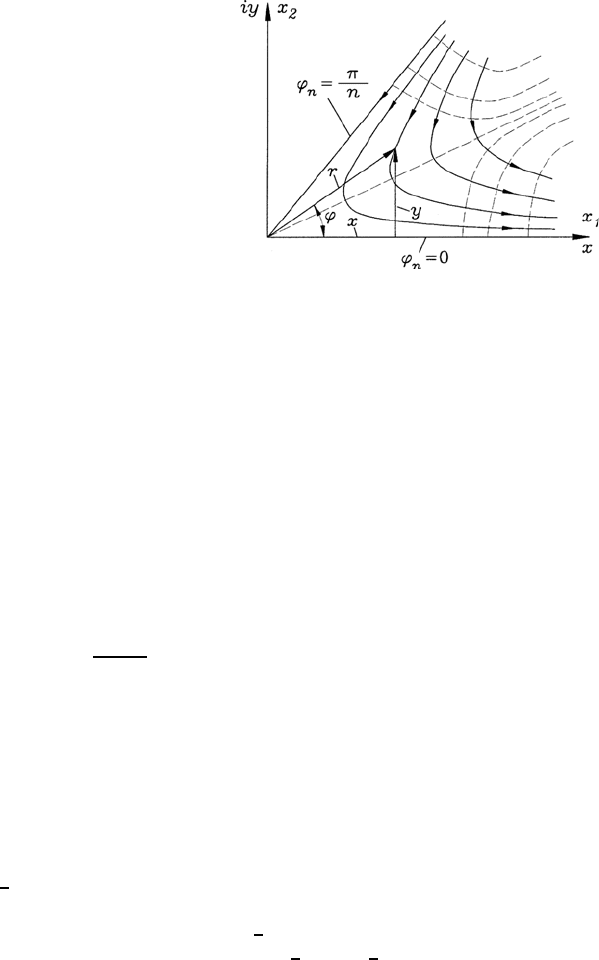
10.4 Corner and Sector Flows 285

Fig. 10.4 General representation

of corner ﬂows and sector ﬂows

From this relationship and taking (10.22) into account, the potential and

stream function can be stated as follows:

Φ(r, ϕ)=Cr

cos(nϕ)andΨ(r, ϕ)=Cr

sin(nϕ). (10.42)

The resulting relationship for the stream function in (10.42) makes it clear

that Ψ (r, ϕ) assumes the values Ψ =0forϕ = 0 and for ϕ = π/n.This

means that the lines ϕ =0andϕ = π/n represent the ﬂow line Ψ =0and

are regarded here as walls of the ﬂow ﬁeld. Between them the stream lines

for Ψ = r

sin(nϕ) = constant are stated. These result for Ψ = constant in

stream lines as they are sketched in Fig. 10.4. The velocity components that

are to be assigned to this ﬂow ﬁeld can be expressed in cylindrical coordinates

as follows:

w(z)=

dF (z)

= nCz

(n−1)

= nCr

(n−1)

{i(n−1)ϕ}

(10.43)

or, rewritten, one obtains:

w(z)=



nCr

(n−1)

(cos(nϕ)+i sin(nϕ))



(−iϕ)

, (10.44)

so that one can state [see (10.31)]:

= nCr

(n−1)

cos(nϕ)andU

= −nCr

(n−1)

sin(nϕ). (10.45)

For

<n<1, one obtains ﬂuid ﬂows around corners as sketched in

Fig. 10.5. Flows around corners are of concern here. They are designated

here, in short, as corner ﬂows. For

<n<1 ﬂows around obtuse-angled

corners are described by (10.40) and for

<n≤

arepresentationofﬂows

is achieved which comprises the ﬂow around acute-angled corners.

For 1 <n<∞. ﬂows in angle sectors result from the complex poten-

tial F (z)=Cz

as sketched for obtuse-angled angle sectors (1 <n<2)

in Fig. 10.6a and for acute-angled ones (2 ≤ n ≤∞) in Fig. 10.6b. As for

0 <ϕ<(π/2n)U

is always positive, whereas U

assumes negative values

286 10 Potential Flows

Fig. 10.5 Flow around (a) acute-angled and (b) obtuse-angled corners

Fig. 10.6 Flow in the (a) obtuse-angled and (b) acute-angled angle sector

in this domain, and as for (π/2n) <ϕ<(π/n)U

becomes negative and

remains negative, the courses of the stream and potential lines result as

sketched in Fig. 10.6.

The planes ϕ

=0andϕ

= π/n represent a stream line. Along this

stream line there are no velocity components in direction normal to the wall.

The velocity changes along the boundary stream line, i.e. the wall boundary

of the ﬂow. The ﬂow in an angle sector with acute angle diﬀers from the

ﬂow in an obtuse-angle ﬂow domain only by the exponent n in the complex

velocity potential.

From the above derivations, it can be seen that the complex potential

(10.40) includes for n = 1 also the uniform ﬂow dealt with in Sect. 10.3.

Another important special case is the ﬂow around a thin plate, which can be

treated as ﬂow around a border with the angle 360

◦

, i.e. this ﬂow is described

by the complex potential:

F (z)=Cz

(

)

. (10.46)

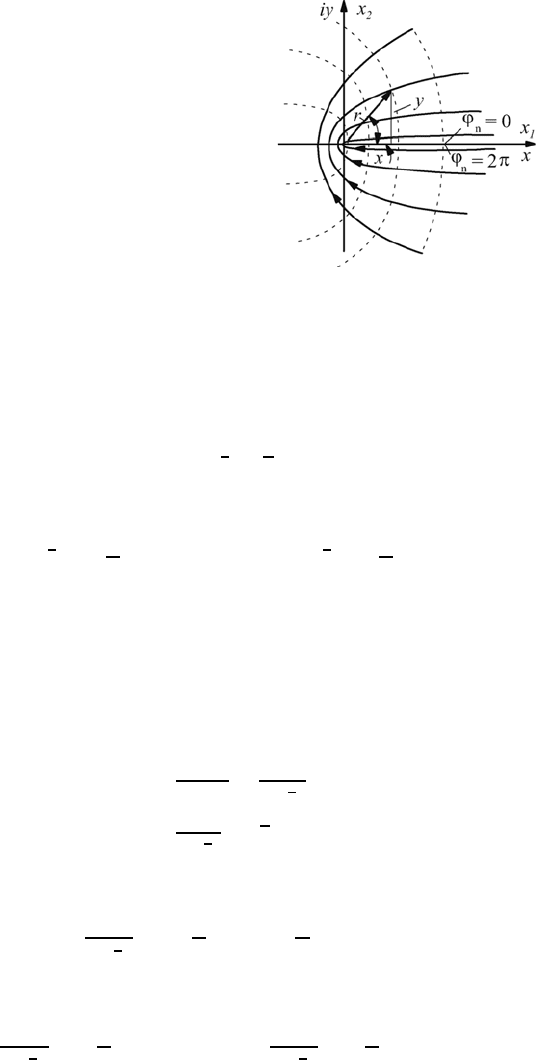
10.4 Corner and Sector Flows 287

Fig. 10.7 Potential ﬂow around the front of an

inﬁnitely thin plate

The proportionality constant is real and the angular area occupied by the

ﬂow is:

0 ≤ ϕ ≤ 2π.

In cylindrical coordinates the complex potential can be written as:

F (z)=Cr

(

)

(

)

. (10.47)

The potential and stream functions can be stated as follows:

Φ(r, ϕ)=Cr

cos





and Ψ(r, ϕ)=Cr

sin





. (10.48)

From the relationship for the stream function, it can be derived that the

lines ϕ =0andϕ =2π correspond to the stream line Ψ =0.Thestream

lines for other ϕ values are described by the stream function in (10.48) and

are sketched in Fig. 10.7. Also indicated are the equipotential lines, which are

also computable according to (10.44). The complex ﬂow velocity is obtained

by diﬀerentiation of the complex potential F (z) to yield:

w(z)=

dF (z)

(

)

(10.49)

(

)

(

−i

)

One can rewrite this relationship as:

w(z)=

(

)



cos





+ i sin





(−iϕ)

. (10.50)

The velocity components U

and U

can therefore be computed as:

(

)

cos





and U

= −

(

)

sin





. (10.51)

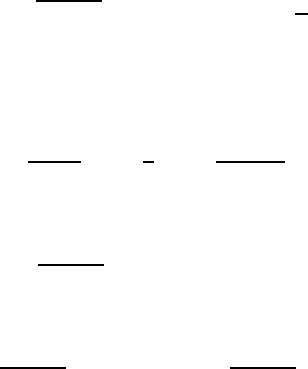
288 10 Potential Flows

These relationships make it clear that the velocity component U

for 0 <

ϕ<2π is negative, whereas U

for 0 <ϕ<πis positive and for π<ϕ<2π

negative. This leads to the stream lines of the ﬂow sketched in Fig. 10.7.

As an important result of the above derivations, one can deduce that the

velocity ﬁeld possesses a singularity at the origin of the coordinate system.

This is caused by the ﬂow around the front corner of the ﬂat plate. This

corner is characterized by extreme values of the velocity ﬁeld. The values of

both velocity components approach ∞ for r → 0.

10.5 Source or Sink Flows and Potential Vortex Flow

When one chooses a complex potential F (z) which is proportional to the

natural logarithm of z, one obtains the complex potential of a source or a

sink ﬂow selecting a real proportionality constant, and depending on whether

one chooses a positive or negative sign, the source ﬂow (+sign) and the sink

(−sign) ﬂow results:

F (z)=±C ln z, (10.52)

or, with z = re

(iϕ)

F (z)=±C [ln r + iϕ]=Φ + iΨ. (10.53)

For the potential and stream functions of the source and sink ﬂow, one

thus obtains:

Φ(r, ϕ)=±C ln rΨ(r, y)=±Cϕ

Φ(x, y)=±C ln



+ y

Ψ(x, y)=±C arctan

. (10.54)

These equations show that the equipotential lines represent circles with r =

constant whereas the stream lines represent radial lines with Φ = constant.

When computing the complex velocity:

w(z)=

dF (z)

= ±C

(x − iy)

+ y

, (10.55)

one obtains for the velocity components:

w(z)=

±C

+ y

(x − iy)=U

− iU

, (10.56)

or, written for U

and U

±Cx

+ y

and U

±Cy

+ y

. (10.57)