Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

References 247

+ ρg

V (H

− H

)

. (8.122)

For the pumping power it results that the electrical power stated in (8.122)

is required to supply the kinetic energy of the ﬂuid leaving the pipe per unit

time, plus the power required per unit time for overcoming the hydrostatic

pressure level.

References

8.1. Becker, E., Technische Str¨omungslehre, Teubner, Stuttgart, 6. ¨uberarb. Auﬂage,

1986.

8.2. Hutter, K., Fluid- und Thermodynamik – Eine Einf¨uhrung, Springer, Berlin,

Heidelberg, New York, 1995.

8.3. Potter, M.C., Foss, J.F., Fluid Mechanics, Wiley, New York, 1975.

8.4. Spurk, J.H., Str¨omungslehre – Einf¨uhrung in die Theorie der Str¨omungen,

Springer, Berlin, Heidelberg, 3. ¨uberarb. Auﬂage, 1993.

8.5. Zierep, J., B¨uhler, K., Str¨omungsmechanik, Springer, Berlin, Heidelberg, New

York, 1991.

Chapter 9

Stream Tube Theory

9.1 General Considerations

The preceding considerations, that covered the derivation of the integral form

of the basic equations of ﬂuid mechanics, can also be used advantageously to

derive simpliﬁed equations applicable to so-called ﬂow ﬁlaments or also called

stream tubes. The latter can be applied to solve some ﬂow problems. For this

purpose, one starts the considerations from ﬂow lines that are introduced as

lines of a ﬂow which, at a certain point in time, possess the direction of the

ﬂow at each point of the ﬂow ﬁeld. One can imagine a so-called ﬂow ﬁlament

to be built up from a bundle of such ﬂow lines and one can make a subdivi-

sion of the entire ﬂow ﬁeld into a multitude of ﬂow ﬁlaments. Furthermore,

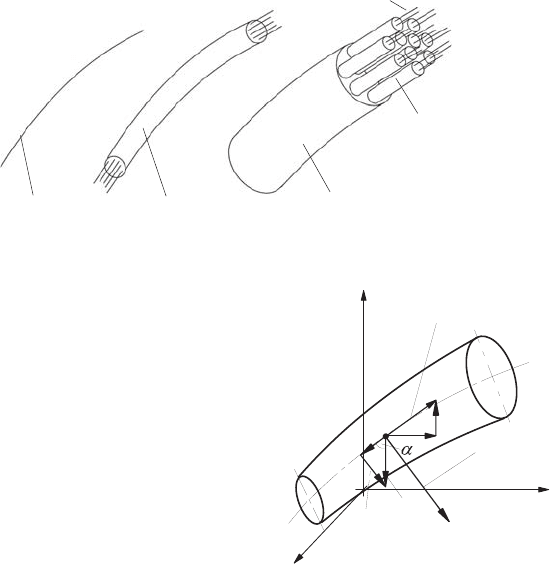
it is possible to bundle ﬂow ﬁlaments to obtain stream tube, as indicated in

Fig. 9.1. For the suggested approach, one has to consider the properties of

ﬂows applied to ﬂow lines, ﬁlaments and stream tubes because this concept

can only be employed advantageously when the ﬂow quantities assigned to

each area of the ﬂow ﬁlament can be considered to be constant over the cross-

section of the ﬂow ﬁlament. This makes it necessary occasionally to choose

the cross-sectional area of a ﬂow ﬁlament suﬃciently small that, for the con-

sidered problem, the assumption of uniform state and ﬂow quantities over the

cross-sectional area of the ﬂow ﬁlament can be fulﬁlled suﬃciently precisely.

For the stationary ﬂow tube theory, it results that the ﬂuid elements con-

stituting a ﬂow ﬁlament constitute this ﬂow ﬁlament permanently. Fluid

particles that are located outside a ﬂow ﬁlament at a certain point in time

can never become components of the considered ﬁlament. Each ﬂuid parti-

cle of a stationary ﬂow area belongs to a certain ﬂow ﬁlament, so that it is

possible to describe the properties of the ﬂow area by the properties of the

considered ﬂow ﬁlaments (Fig. 9.2).

249

250 9 Stream Tube Theory

Stream or flow line

Stream or flow

filament

Flow line

Flow

filament

Stream tube

Fig. 9.1 Flow or stream line, ﬂow or stream ﬁlament and stream tube

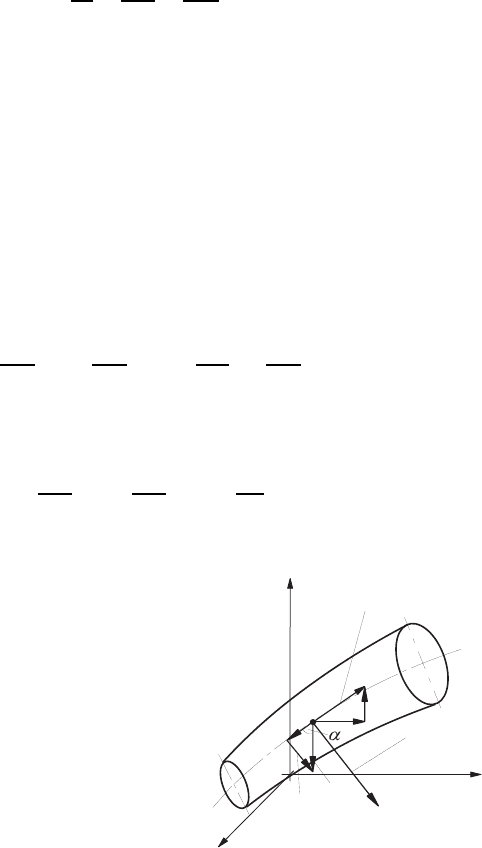
Fig. 9.2 Stream with introduced n–s

coordinate system

Flow direction

Normal to

flow direction

To simplify the considerations on ﬂow ﬁlaments, the following assumptions

for ﬂow ﬁlaments are introduced:

• A ﬂow ﬁlament is always completely ﬁlled with the ﬂuid for which the ﬂow

considerations are carried out.

• The cross-sectional area changes along a ﬂow ﬁlament are small

• A ﬂow ﬁlament is assumed to be only slightly curved in the ﬂow direction

Although the assumptions introduced above for ﬂow ﬁlaments have con-

siderable limitations, the derivations given in the following sections show

that the introduction of ﬂow ﬁlaments, with the above properties, into ﬂuid

mechanical considerations, leads to equations through which physically very

illustrative solutions of ﬂow problems can be derived.

The considerations carried out on the basis of ﬂow ﬁlaments show that in

some cases the properties of entire ﬂow ﬁelds can be described by the prop-

erties of ﬂow ﬁlaments. When the ﬂow quantities change only slightly over

the entire cross-sections of internal ﬂows, the basic equations derived for ﬂow

ﬁlaments of small dimensions can also be employed to acquire the most im-

portant properties of internal ﬂows by a one-dimensional ﬂow theory. For this

purpose, the internal ﬂow is treated as a single stream tube. The justiﬁcation

9.2 Derivations of the Basic Equations 251

for this is given only, however, when friction inﬂuences are small or can be

neglected for ﬁrst considerations of ﬂow problems.

9.2 Derivations of the Basic Equations

9.2.1 Continuity Equation

The derivation of the continuity equation for a ﬂow ﬁlament builds up on

the diﬀerential form of mass conservation as derived in Sect. 5.2, and which,

after integration over a control volume, and having employed Gauss’s integral

theorem, can be stated as:

∂ρ

∂t

∂ (ρU

)

∂x

=0 ;



∂ρ

∂t



dV +

ρU

=0 (9.1)

where V

is identical with the considered control volume and O

is its

outer surface. Exchanging in the ﬁrst term of this equation integration and

diﬀerentiation, one obtains:

∂

∂t

ρdV +

ρU

=0 ;

∂M

∂t

= −

ρU

(9.2)

Applying this form of the mass conservation equation to a ﬂow ﬁlament and

considering that the same mass ﬂux passes through all the cross-sectional

areas of the ﬂow ﬁlament,

∂M

∂t

= 0 (stationary ﬂow conditions) the following

results, i.e. the mass inﬂows and outﬂows for a ﬂow ﬁlament are the same:

ρU

; A

s,A

= A

s,B

(9.3)

where the plane of the area A stands perpendicular to the ﬂow direction s.

Therefore, one can conclude that the mass ﬂow ˙m = ρAU

through the

cross-sectional area along a ﬂow ﬁlament is constant.

In the derivations carried out above, it was already said that because

of small cross-sectional area changes in the ﬂow ﬁlaments A, ρ and U

can

be set to be constant over A. When one wants to apply the considerations

also to stream tubes, as shown in Fig. 9.3, a more reﬁned approach is neces-

sary. It must be taken into account that the assumption of constant density

and velocity U

in the presence of large cross-sectional areas is only permit-

ted conditionally. The introduction of cross-sectionally averaged quantities is

necessary, as will be shown below.

When carrying out the following averaging, with the use of the mean value

theorem of integration:

ρU

= −

ρU

252 9 Stream Tube Theory

F =

const

(F )

F(s)

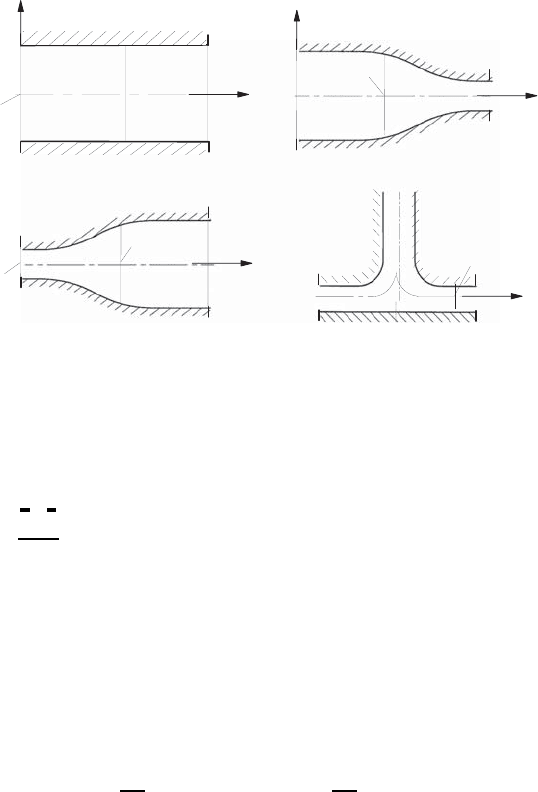
Pipe flow

Nozzle flow

Diffusor flow

Flow with directional change

F(s)

Fig. 9.3 Flows which can be computed one-dimensionally by the approximation

method introduced by stream tubes

it can be stated for stationary ﬂow conditions that



∂M

∂t

= −

ρU

;



ρU





ρU



(9.4)

This relationship for the momentum ﬂows through the cross-sectional areas

A and B is often simpliﬁed further in stream tube theory, by assuming

ρU

˜ρ

, i.e. (9.4) is employed as follows:

˜ρ

s,A

=˜ρ

s,B

= ρU

(9.5)

where ˜ρ

and ˜ρ

,andalso

s,A

and

s,B

are deﬁned as follows:

˜ρ

ρdf and

df (9.6)

The above derivations make it clear that the employment of the simpliﬁed

integral form of the continuity equation ˜ρ

= constant is only justiﬁed for

ﬂows that have no strong variation in density or velocity over the ﬂow cross-

section of a considered stream tube. Taking this assumption into account,

(9.5) is used in the following derivations. Since in the following considera-

tions, strong variations of the quantities ρ and U

over the cross-section are

excluded, it is also justiﬁed to introduce local quantities in (9.5) as a valid

approximation.

In ﬂuid mechanics, a number of questions arise relating to inﬁnitesimal

changes of a thermodynamic state or a ﬂow quantity when inﬁnitesimal

9.2 Derivations of the Basic Equations 253

changes of other parameters take place. For this reason, the continuity

equationisoftenappliedinaformderivedbelow:

Diﬀerentiation of (9.5) gives:

d˜ρ +˜ρA

+˜ρ

UdA

=0 (9.7)

The division of (9.7) by (9.5) leads to a further form of the continuity equation

which is employed in some cases in the following sections:

d˜ρ

˜ρ

=0 (9.8)

The equation expresses how, e.g., the velocity of a ﬂuid will change in a

relative manner when common relative changes in density and cross-sectional

area occur.

9.2.2 Momentum Equation

Solutions of ﬂow problems on the basis of the stream tube theory require the

inclusion of the momentum equations. However, these have to be transformed

to the ﬂow ﬁlament or stream tube coordinates (Fig. 9.4). Starting from the

general momentum equation:



∂U

∂t

+ U

∂U

∂x



= −

∂P

∂x

−

∂τ

∂x

+ ρg

(9.9)

and neglecting the molecular momentum transport terms acting on the ﬂow

ﬁlament, the following form of the momentum equations results:



∂U

∂t

+ U

∂U

∂s



= −

∂P

∂s

+ ρg

(9.10)

Fig. 9.4 Expression of the momentum

equation for the ﬂow ﬁlament

Flow direction

Normal to

flow direction

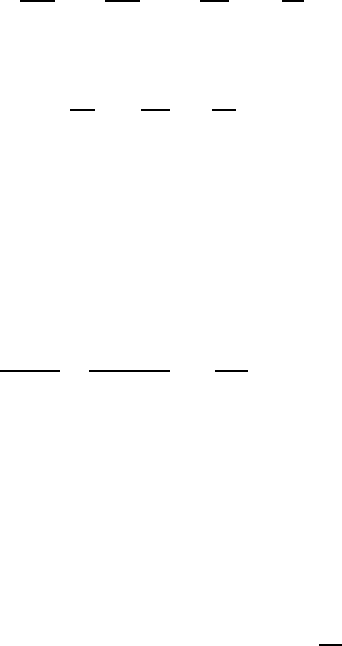
254 9 Stream Tube Theory

with g

= −g cos α and cos α =dz/ds,sothat:



∂U

∂t

+ U

∂U

∂s



= −

∂P

∂s

− ρg

(9.11)

In an analogous way, it can be derived that the momentum equation in

the n direction is

= −

∂P

∂n

− g

(9.12)

where the direction of z needs to be chosen in the negative direction of the

gravitational ﬁeld.

This equation expresses that for straight ﬂow ﬁlaments, i.e. R →∞,the

pressure variation vertical to the ﬂow direction is given only by the grav-

itation. When the gravitational forces are negligible, the pressure over the

cross-section of a non-curved ﬂow ﬁlament is constant.

Starting from the general momentum equation in Eulerian form, i.e.

neglecting the molecular momentum loss terms:

∂(ρU

)

∂t

∂(ρU

)

∂x

= −

∂P

∂x

+ ρg

(9.13)

and integrating these over a control volume corresponding to the entire space

of a ﬂow ﬁlament, one obtains for stationary ﬂow conditions:

ρU

df = −

P df

ρg

dV (9.14)

For the special inﬂow and outﬂow conditions at the areas A

and A

of a

ﬂow ﬁlament, it can thus be stated that

−ρ

s,A

+ ρU

s,B

=+P

− P

−

ρg

(Ads) (9.15)

or rewritten for g = 0, i.e. neglecting gravity:

ρU

+ PA

= constant (9.16)

This form of momentum equation is employed for many problem solutions

in ﬂuid mechanics and will also be employed in the sections to follow in this

book.

9.2.3 Bernoulli Equation

When carrying out ﬂuid mechanics considerations, often the pressure and

the velocity changes in the ﬂow direction are of interest. Such changes can,

when resulting only from mechanical energy changes, be determined from the

9.2 Derivations of the Basic Equations 255

mechanical energy equation. This equation can be stated in general form as

follows (see Sect. 5.5):



+ G



= −

∂(PU

)

∂x

+ P

∂U

∂x

−

∂(τ

)

∂x

+ τ

∂U

∂x

(9.17)

When carrying out considerations neglecting the molecular-dependent en-

ergy transport on molecular dissipations terms, i.e. setting τ

= 0, then one

obtains for ρ = constant and thus

∂U

∂x

=0:



+ G



= −

∂(PU

)

∂x

= −U

∂P

∂x

(9.18)

In the presence of only stationary pressure ﬁelds the following holds:

∂P

∂t



∂P

∂x

= U

∂P

∂x

(9.19)

so that under these conditions one can write:



+ G



= −

(9.20)

For G = −x

, (9.20) can be written as:



− x



= 0 (9.21)

which leads for j = s to the statement of the Bernoulli equation for a ﬂow

ﬁlament:

− g

s = constant (9.22)

Considering that −g

s = gh, one obtains the ﬁnal form of the Bernoulli

equation:

+ gh = constant (9.23)

This equation can be interpreted physically such that the mass ﬂux ˙m,ﬂowing

into a ﬂow ﬁlament per unit time, introduces the kinetic energy ˙m

,the

pressure energy ˙mP υ =˙m

and the potential energy ˙mgh as total energy.

The sum of these three parts along the ﬂow ﬁlament cannot change, i.e. the

total energy is constant along the ﬂow ﬁlament. As at the same time ˙m =

constant holds, (9.23) results from all these considerations of mass and energy

conservations.

256 9 Stream Tube Theory

9.2.4 The Total Energy Equation

The above considerations of the Bernoulli equation must also include the

expansion work when carrying out energy considerations for compressible

media. Considering the derivations in Chap. 5, the equation for the total

energy has to be employed instead of the above treated mechanical energy

equation. According to (5.68), the equation of the total energy can be stated

as follows:



e +

+ G



= −

∂ ˙q

∂x

−

∂(PU

)

∂x

−

(τ

)

(9.24)

Neglecting the contributions in the equation due to the molecular-dependent

heat and momentum transport, i.e. ˙q

=0andτ

= 0, the following equation

results for g ≈ 0:

∂

∂t



ρe +

ρU



∂

∂x





ρe +

ρU



∂

∂x

(PU

) (9.25)

For stationary ﬂow processes, i.e. neglecting the time derivative terms, the

following equation holds:

∂

∂x



ρU



e +



= 0 (9.26)

Introducing the enthalpy h = e + P/ρ, one obtains for the energy equation

for stationary ﬂows of compressible media:

h +

= constant (9.27)

When carrying out the above considerations for stream tubes, one obtains

also the relationship stated in (9.27) for area-averaged quantities:

h +

= constant (9.28)

The sum of the area-averaged enthalpy of a ﬂowing ﬂuid and the area-

averaged kinetic energy per unit mass of the ﬂuid is a constant for adiabatic

ﬂows that are free of viscosity and when gravity inﬂuences are negligible.

With this, the following equations for the computation of ﬂows in stream

tubes result:

Flows of incompressible ﬂuids:

• Mass conservation: ˜ρ

= constant (9.29)

• Momentum conservation: ˜ρ

+ PA

= constant (9.30)

• Mechanical energy equation:



˜ρ

+ g

= constant (9.31)

9.3 Incompressible Flows 257

Flows of compressible ﬂuids:

• Mass conservation: ˜ρ

= constant (9.32)

• Momentum conservation: ˜ρ

+ PA

= constant (9.33)

• Thermal energy equation:

h = constant (9.34)

9.3 Incompressible Flows

9.3.1 Hydro-Mechanical Nozzle Flows

The ﬂow problem shown in Fig. 9.5 can be solved, neglecting the friction

forces, with the aid of the ﬂow tube theory, in order to obtain a ﬁrst overview

of the ﬂow processes taking place in converging pipes.

When applying one-dimensional ﬂow computations, for the ﬂow in cross-

section A, a velocity can be stated which is constant over the entire tube

diameter:

˙m

(9.35)

Since the continuity equation holds:

; U

(9.36)

From the Bernoulli equation:

(9.37)

From this P

is computed as:

= P

− U

= P





− 1

(9.38)

F/2

Control volume

Fig. 9.5 Nozzle ﬂow at the end of a pipe