Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

258 9 Stream Tube Theory

The ﬂange force F on the control volume in Fig. 9.5 is computed from the

integral momentum equation as follows:

−ρU

+ ρU

−P

+ P

  

−

−P

)

= F (9.39)

or, after rearrangement, in consideration of (9.38):

−



2 − 2



−



− 1



= F (9.40a)

and after further rearrangement:

−



1 −



= F (9.40b)

On inserting the corresponding relationships for U

from (9.35), one obtains

for the ﬂange force F

A = −

˙m



1 −



(9.41)

The force applied by the ﬂange on the examined nozzle part proves to be

positive, so that the supporting surface of the ﬂange receives a negative force

F . The screws in the ﬂange can therefore be regarded to be force free as far

as any contribution from the ﬂow is concerned. The nozzle is pressed on to

the ﬂange.

9.3.2 Sudden Cross-Sectional Area Extension

In practical ﬂuid mechanics, often pipes of diﬀerent cross-sections are lined

up and ﬂows proceed through them. In this way, viewed in the ﬂow direction,

internal ﬂows result that are exposed to sudden cross-section widenings, as

shown in Fig. 9.6. In this manner separation areas are generated whose inﬂu-

ence on the ﬂow can be understood from the following considerations. When

treating ﬂows with sudden changes in their cross-sectional area, mass conser-

vation between the planes A and B of the pipe ﬂow exists, and thus yields

from the continuity equation:

˙m

= U

(9.42)

Hence the velocities U

and U

can be determined by the given mass ﬂow

˙m, if the density of the ﬂuid is known, and also the cross sectional areas.

In the case of ﬂows passing through the considered region without losses,

the following diﬀerence in pressure would result between the planes A and B,

which can be computed from the Bernoulli equation:

9.3 Incompressible Flows 259

verl

{

ideal

real

Pressure distribution

Separation

region

Separation

region

Fig. 9.6 Carnot’s impact diﬀusor

∆P

ideal

=(P

− P

)

ideal



1 −



(9.43)

Under real conditions, as indicated in Fig. 9.6 by the occurrence of the sep-

aration areas, the following momentum equation results:

F = ρU

− ρU

+ P

− P

(9.44)

When one neglects the contributions to the force F by momentum losses at

the pipe walls, then the force F can be computed as the pressure force on

the ring surface after the sudden expansion of the pipe, i.e. as

F = P

− d

(9.45)

Thus one obtains for the pressure diﬀerence

∆P

real

=(P

− P

)

real

= ρU



1 −



, (9.46)

so that a pressure loss (Carnot’s momentum loss) can be determined as

follows:

∆P

loss

=∆P

ideal

− ∆P

real



1 −



− U

(9.47)

For D →∞resultsasamaximumvaluefor∆P

loss

, the discharge

pressure loss. This means that there is no diﬀusor available to convert the

“dynamic pressure”

ρU

back into “static pressure”.

260 9 Stream Tube Theory

9.4 Compressible Flows

9.4.1 Inﬂuences of Area Changes on Flows

The general treatment here provides information on what eﬀect cross-sectional

changes in ﬂow channels have on ﬂuid ﬂows, i.e. to what extent and in which

way area changes determine the distribution of velocity, pressure, density and

temperature along the channel. The equations that were derived in Sect. 9.2

are employed, i.e. the continuity equation reads:

˜ρ

A = constant (9.48)

Equation (9.48) can be written in diﬀerential form as:

d˜ρ

˜ρ

= 0 (9.49)

According to the considerations in Sect. 9.2, the variation of the velocity

in the ﬂow direction can be described, as a ﬁrst approximation, by Euler’s

equation, reduced for one-dimensional ﬂows, i.e.

˜ρ

= −

d˜ρ

(9.50)

On the basis of the energy equation, written for reversible adiabatic ﬂuid

ﬂows, the following relationship holds:

˜ρ

= constant (9.51)

Under these adiabatic conditions, the diﬀerentiation of

P with respect to ρ

yields the sound velocity c:

˜c

d˜ρ

(9.52)

Equation (9.52) introduced into (9.50) yields the following relationship:

˜ρ

= − ˜c

d˜ρ

(9.53)

When one introduces the Mach number Ma of the ﬂow as:

Ma =

˜c

(9.54)

9.4 Compressible Flows 261

(9.53) can be written as:

d˜ρ

˜ρ

= −

(9.55)

Inserting the density variation in (9.55) in (9.49), one obtains:

−

= 0 (9.56)

−1

(1 −

)

(9.57)

When one takes into consideration that subsonic ﬂows are given by

Ma < 1

and supersonic ﬂows by

Ma > 1, the above relationship expresses:

• In the presence of a subsonic ﬂow (

Ma < 1), a decrease in the cross-

sectional area of a ﬂow channel in the ﬂow direction is linked to an increase

in the ﬂow velocity. An increase in the channel cross-sectional area in the

ﬂow direction results in a decrease in the ﬂow velocity (see Fig. 9.7).

• In the presence of a supersonic ﬂow (

Ma > 1), a decrease in the cross-

sectional area of a ﬂow channel in the ﬂow direction is linked to a decrease

in the ﬂow velocity. An increase in the ﬂow cross-section in the ﬂow

direction results in an increase in the ﬂow velocity (see Fig. 9.8).

In addition to the changes in the ﬂow velocity, caused by changes in the

cross-sectional areas, the changes in pressure, density and temperature of the

ﬂowing ﬂuid are also of interest. From (9.51), it can be seen that the relative

change in density always has the opposite sign to the change in velocity,

i.e. the density increases in the ﬂow direction when the velocity decreases

and vice versa. In the region of subsonic ﬂow, the locally present relative

Fig. 9.7 Inﬂuence of a change in the ﬂow cross-section on a subsonic ﬂow

262 9 Stream Tube Theory

Fig. 9.8 Inﬂuence of a change in the ﬂow cross-section on a supersonic ﬂow

change in density is smaller than the local relative change in velocity. In the

region of supersonic ﬂow, the locally present relative change in density is

larger than the relative change in velocity. The changes in the density for the

corresponding changes in cross-sectional area changes of the ﬂow channel are

given by the relationship:

d˜ρ

˜ρ

(1 −

)

(9.58)

With regard to the pressure variation, the following considerations can be

carried out. From the adiabatic pressure-density relationship (9.51), the

following results:

P =

˜ρ

κ˜ρ

(κ−1)

d˜ρ = κ

˜ρ

d˜ρ (9.59)

Therefore, for the local relative change in pressure one can derive:

= κ

(9.60)

or with regard to the local relative change in the cross-sectional area of the

ﬂow, the following relative change in pressure results:

(1 −

)

(9.61)

Finally, it is necessary to consider the variations in temperature. For this

purpose, the state equation for ideal gases is diﬀerentiated:

−

d˜ρ

˜ρ

= Rd

(9.62)

9.4 Compressible Flows 263

or rewritten in the following form:

−

d˜ρ

˜ρ

(9.63)

Hence, knowing

d˜ρ

˜ρ

and

, the following relationship for the temperature

changes results:

= −(κ − 1)

(9.64)

The locally occurring relative change in temperature has the opposite sign

to the local relative change in velocity. The relative changes in temperature

are weaker than the corresponding relative changes in density. With regard

to the relative area change of the ﬂow cross-section, it results that

(κ − 1)

(1 −

)

(9.65)

The considerations stated for the ﬂow velocity variations in supersonic and

subsonic ﬂows, which are sketched in Figs. 9.7 and 9.8, can also be carried

out for the variations in pressure, density and temperature with the aid of

the above equations.

Another important result of the above derivations can be stated through

a rearrangement of the relationships derived above, such that the following

equation holds:

(1 −

) (9.66)

This relationship expresses that the condition for achieving the sound velocity

is given by dA = 0, i.e.

Ma = 1. Since for the second derivative of A

(

− 2) (9.67)

for

Ma = 1 the condition for some ﬂow to exist is given by a minimum of the

ﬂow cross-section. Further considerations of changes if errors sectional area

are given in refs. [9.1] to [9.5].

9.4.2 Pressure-Driven Flows Through Converging

Nozzles

In many technical plants, ﬂows of gases occur which are to be classiﬁed into a

group of ﬂows that take place between reservoirs with diﬀering pressure lev-

els. Gases, for example, are often stored under high pressure in large storage

reservoirs, in order to be discharged through conduits for the intended pur-

pose when need arises. This discharge can be idealized as a “equalization ﬂow”

264 9 Stream Tube Theory

between two reservoirs or two chambers of which one represents the storage

reservoir under pressure, while the environment represents the second reser-

voir. In the following considerations it is assumed that both reservoirs are very

large, so that constant reservoir conditions exist during the entire “equaliza-

tion ﬂow” under investigation. These are assumed to be known and are given

by the pressure P

, the temperature T

, etc., in the high-pressure reservoir,

and also through the pressure P

and temperature T

for the low-pressure

reservoir. The compensating ﬂow takes place via a continually converging

nozzle as indicated in Fig. 9.9, whose largest cross-section thus represents the

discharge opening of the high pressure reservoir, whereas the smallest nozzle

cross-section represents the inlet opening into the low-pressure reservoir.

When one wants to investigate the ﬂuid ﬂows taking place in the above

equalization ﬂow in more detail, the ﬁnal equations for ﬂows through chan-

nels, pipes, etc., derived in Sect. 9.2 can be used:

˜ρ

A = constant (9.68)

h +

= constant;

˜ρ

= constant (9.69)

˜ρ

= R

T (9.70)

With (9.68)–(9.70), a suﬃcient number of equations exists to determine the

changes in the area-averaged velocity and the area-averaged thermodynamic

state quantities of the ﬂowing gas. Hence the velocity, pressure, temperature

and density along the x

axis, shown in Fig. 9.9, can be found by solving this

set of equations.

When one considers that, based on the assumption of a large high-pressure

reservoir there is the constant pressure P

and the velocity (U

)

=0,then

for the velocity U

at each point x

of the nozzle the following relationship

can be stated to be valid:

Container 1

Container

x =0

x =L

F(x )

Fig. 9.9 Flow between two reservoirs through a converging nozzle

9.4 Compressible Flows 265

h +

= h

(9.71)

Taking into account that the enthalpy for an ideal gas can be stated as c

and moreover that the ideal gas equation (9.70) holds, (9.71) can be rewritten

as follows:

R˜ρ

κ − 1

˜ρ

κ − 1

(9.72)

The velocity U

is thus linked to the change in the pressure along the axis of

the nozzle as follows:

;

2κ

κ − 1

−

˜ρ

(9.73)

The above equation indicates that for

P = 0, i.e. for the outﬂow into a

vacuum, a maximum possible ﬂow velocity develops which is given by the

state of the reservoir only:

max

2κ

κ − 1



(9.74)

Standardizing the ﬂow velocity U

, existing at a point x

,withU

max

,one

obtains:

max

1 −

P · ρ

˜ρ

(9.75)

or rewritten by taking the ideal gas equation into account:

max

1 −

(9.76)

Linking the adiabatic equation (9.86) to the state (9.70) leads to the following

relationships:



˜ρ



κ−1

and

κ−1

(9.77)

Thus the following equations hold:

max

;

1 −



˜ρ



κ−1

(9.78)

266 9 Stream Tube Theory

and

max

;

⎡

⎣

1 −

κ−1

⎤

⎦

(9.79)

On choosing the normalized velocity (

max

) as a parameter for the repre-

sentation of the ﬂow in the nozzle, the distributions of pressure, density and

temperature along the nozzle can be stated as follows:

⎡

⎣

1 −

max

⎤

⎦

κ−1

(9.80)

˜ρ

⎡

⎣

1 −

max

⎤

⎦

κ−1

(9.81)

⎡

⎣

1 −

max

⎤

⎦

(9.82)

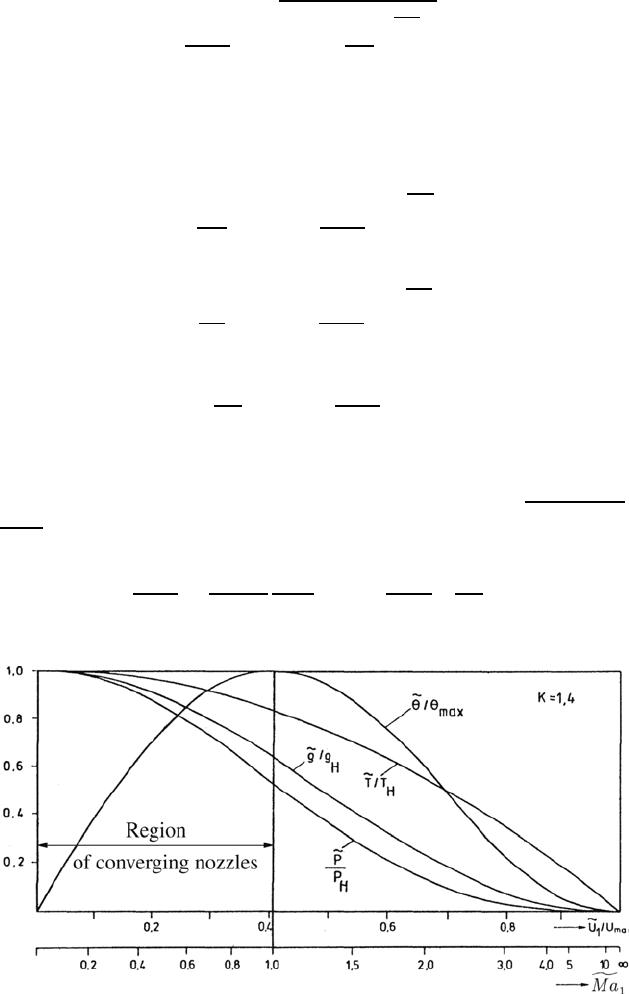
These relationships are shown in Fig. 9.10 as functions of (

max

). Also,

along the (

max

) axis, the corresponding Mach number of the ﬂow is

plotted, which under consideration of the relationship c =



(dP/ dρ)

√

κRT can be shown to be identical with

max

κR

κ − 1

(9.83)

Fig. 9.10 Distributions of the pressure, density and temperature as a function of

the local normalized velocity or as a function of the local Mach number

9.4 Compressible Flows 267

When one considers the relationship derived above for (T/T

), in (9.77), one

obtains for the Mach number the following dependence on (

max

Ma =

;

κ − 1

⎧

⎪

⎨

⎪

⎩

max

⎡

⎣

1 −

max

⎤

⎦

⎫

⎪

⎬

⎪

⎭

(9.84)

Hence a Mach number of the ﬂow can be assigned to each value of an area-

averaged velocity normalized with the maximum velocity.

All quantities which are stated in (9.80)–(9.82) can also be written as

functions of the Mach number

Ma. This in turn can be considered as an

area-averaged ﬂow quantity describing the distributions of the ﬂow along the

axis.

For the derivation showing the dependence of the pressure, density and

temperature on the Mach number of the ﬂow, shown graphically in Fig. 9.10,

(9.71) is written as follows:

T +

= c

(9.85)

By division with c

T one obtains

=1+

κR

=1+

κ − 1

(9.86)

or for the reciprocal

2+(κ − 1)



(9.87)

This equation makes it clear that there is a relationship between the area-

averaged temperature at a location on the x

axis and the Mach number

existing at the same point of the ﬂow. Hence it becomes clear that for each

point x

the temperature can be computed when the high-pressure reservoir

temperature is given and the Mach number of the ﬂow is known.

Taking into account the adiabatic equation, the relationship between the

pressure

P and reservoir pressure P

is given by

κ−1

2+(κ − 1)



κ−1

(9.88)

and the corresponding relationship for the density is

˜ρ

κ−1

2+(κ − 1)



κ−1

(9.89)