Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

10.5 Source or Sink Flows and Potential Vortex Flow 289

In (10.55), w(z) can also be written in r − Φ coordinates:

w(z)=

±C

= ±

(−iϕ)

. (10.58)

A comparison of (10.58) with (10.31) shows that the following relationships

hold:

= ±

and U

=0. (10.59)

The velocity component U

decreases with 1/r; however, this velocity has

a singularity in origin at r = 0 in the selected coordinate system.

A ﬂow thus comes about which is sketched in Fig. 10.8 for the source ﬂow

and which is purely radial.

The volume ﬂow released per unit time and unit depth by the source,

characterizing the strength of the source, is given by:

Q =

2π

r dϕ = C2π, (10.60)

so that the complex potential for the source or the sink ﬂow can be written

as follows:

(+) = source ﬂow

F (z)=±

2π

ln z

(−) = sink ﬂow

. (10.61)

Fig. 10.8 Representation of the potential and stream lines for source ﬂows

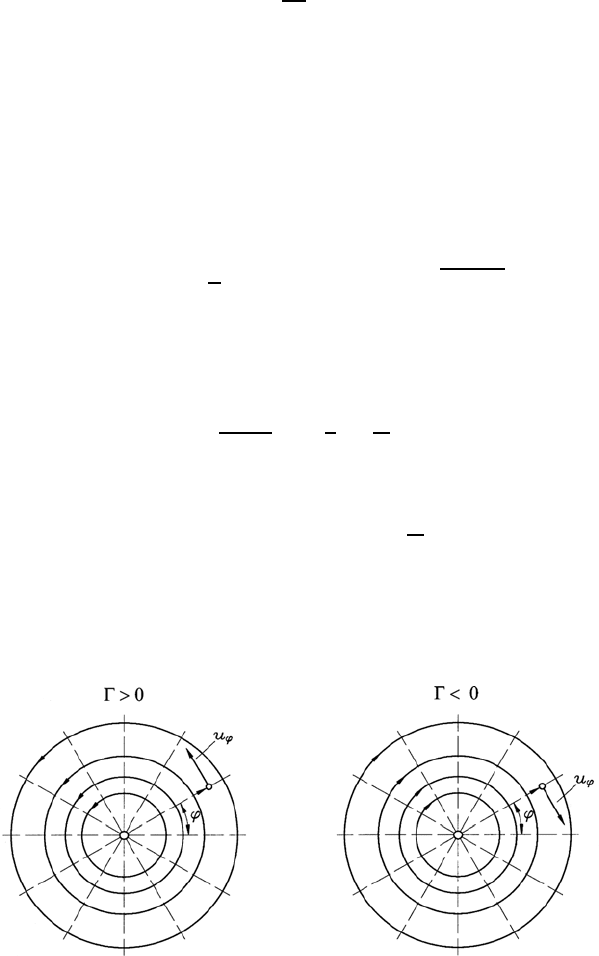
290 10 Potential Flows

When the source or sink does not lie at the origin of the coordinate system

but at the point z

,oneobtains:

F (z)=±

2π

ln(z − z

). (10.62)

When considering a potential z proportional to the natural logarithm,

in which the proportionality constant is imaginary, one obtains F (z)ofa

potential vortex:

F (z)=iC ln z = C(−ϕ + i ln r). (10.63)

For the potential and stream functions one can deduce from this that:

Φ(r, ϕ)=−Cϕ and Ψ(r, ϕ)=C ln r, (10.64)

or:

Φ(x, y)=−C arctan

and Ψ (x, y)=C ln



+ y

. (10.65)

These relationships show that the equipotential radially and outward going

lines represented by Φ = constant whereas the stream lines are circles with

r = constant (Fig. 10.9). For the complex velocity, one can derive:

w(z)=

dF (z)

= iC

= i

(−iϕ)

. (10.66)

By comparing (10.66) and (10.31), one can deduce that:

=0 and U

= −

. (10.67)

This resulting ﬂow ﬁeld is that of a potential vortex with a characteristic

decrease of the circumferential velocity with distance from the vortex center.

When deﬁning the strength of the potential vortex by the circulation Γ ,one

Fig. 10.9 Stream lines and equipotential lines of the potential vortex

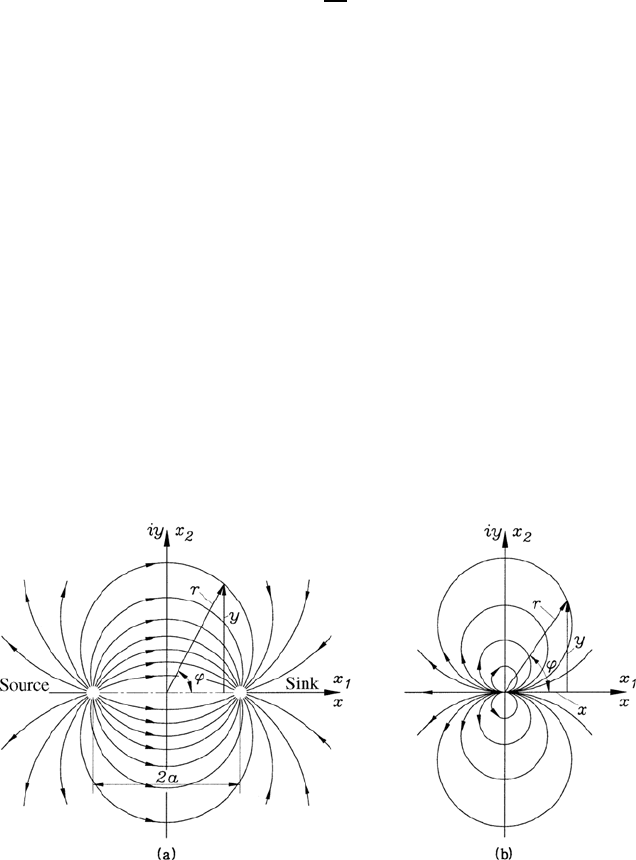
10.6 Dipole-Generated Flow 291

can derive:

Γ =

(

ds =

2π

r dϕ = −2πC. (10.68)

With this the potential vortex rotating in the mathematically positive

direction (Γ is positive), the complex potential can be stated as follows:

F (z)=−

2π

i ln z. (10.69)

When the sign is positive, a potential vortex rotating in the mathematically

negative direction results with Γ being positive.

A strict distinction has to be made between the potential vortex and vortex

motions whose ﬂow ﬁelds possess rotations, e.g. vortices result where the

entire ﬂow ﬁeld rotates analogously to the rotation of a solid body. The

ﬂow ﬁeld of the potential vertex is irrotational. The entire circulation of a

potential vertex is limited to the vortex-center line where the total circulation

is located.

10.6 Dipole-Generated Flow

In this section, a potential ﬂow will be discussed which is deﬁned as dipole-

generated ﬂow and results as a limiting case of the superposition of a source

ﬂow with a sink ﬂow. Considered is a source with a strength

Q which is

located on the x-axis at a distance −a from the origin of a coordinate system

and a sink of the same strength, which has been arranged on the x-axis at a

distance +a as shown in Fig. 10.10a.

Fig. 10.10 Flow lines of (a) source and sink ﬂows and (b) a dipole-generated ﬂow

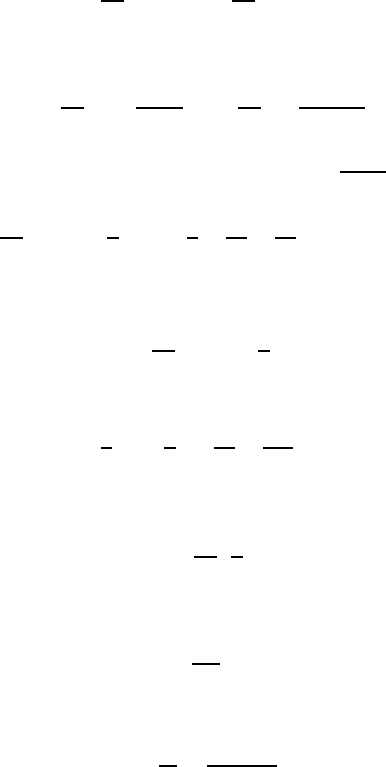
292 10 Potential Flows

When the distances ±a are reduced, the source and the sink of the con-

sidered potential ﬂow move closer together until, for the limiting case a → 0,

they coincide in the coordinate origin and thus result in the dipole-generated

ﬂow sketched in Fig. 10.10b.

It is the task of the following derivations to ﬁnd the complex potential of

the dipole-generated ﬂow and to derive and discuss, based on the carried out

derivations, the ﬂow ﬁeld of the dipole generated ﬂow.

The complex potential of the combined source and sink ﬂow sketched in

Fig. 10.10 can be stated as the sum of the complex potential of both ﬂows:

F (z)=

2π

ln(z + a) −

2π

ln(z − a), (10.70)

or rewritten in the following form:

F (z)=

2π





z + a

z − a



2π



1+a/z

1 − a/z



. (10.71)

When carrying out a series expansion for the term



1−a/z



,oneobtains:

F (z)=

2π









+ ...



, (10.72)

or, after performing multiplication and truncation after the linear terms, one

obtains:

F (z)=

2π



1+2



. (10.73)

When one carries out another series expansion:



1+2



− 2

∓ ..., (10.74)

one obtains for small values (a/z):

F (z)=

2π

. (10.75)

With the strength of the dipole generated ﬂow being characterized as:

D =

the following complex potential results for the dipole-generated ﬂows:

F (z)=

(x + iy)

. (10.76)

10.7 Potential Flow Around a Cylinder 293

For the potential and stream functions, the following expressions can be

derived:

Φ(r, ϕ)=

+ y

and Ψ (r, ϕ)=

−Dy

+ y

Φ(r, ϕ)=

cos ϕ and Ψ (r, ϕ)=

−D

sin ϕ. (10.77)

The ﬂow lines and equipotential lines are indicated in Fig. 10.10b.

For the complex velocity, one can derive:

w(z)=

dF (z)

= −

(−i2ϕ)

, (10.78)

or rewritten in the following form:

w(z)=−

(cos ϕ − i sin ϕ)e

(−iϕ)

. (10.79)

From this result, the following expressions for the velocity components

result:

= −

cos ϕ and U

= −

sin ϕ. (10.80)

The signs of these velocity components conﬁrm the direction of the ﬂow

indicated in Fig. 10.10b.

10.7 Potential Flow Around a Cylinder

The signiﬁcance of the dipole-generated ﬂow discussed above lies in the fact

that its complex potential can be superimposed with the complex potential

of the uniform ﬂow parallel to the x-axis; in this way, a complex potential

arises which describes the ﬂow around a cylinder. The simple superposition

of the F (z) functions of these two kinds of ﬂows is permitted as the partial

diﬀerential equations, derived from the basic equations of ﬂuid mechanics,

are linear for the potential and stream function. By addition of the complex

potentials for the constant ﬂow parallel to the x-axis and for the dipole-

generated ﬂow, one obtains the following relationship:

F (z)=U

z +

= U

(iϕ)

(−iϕ)

, (10.81)

which is equivalent to:

F (z)=U

r(cos ϕ + i sin ϕ)+

(cos ϕ − i sin ϕ). (10.82)

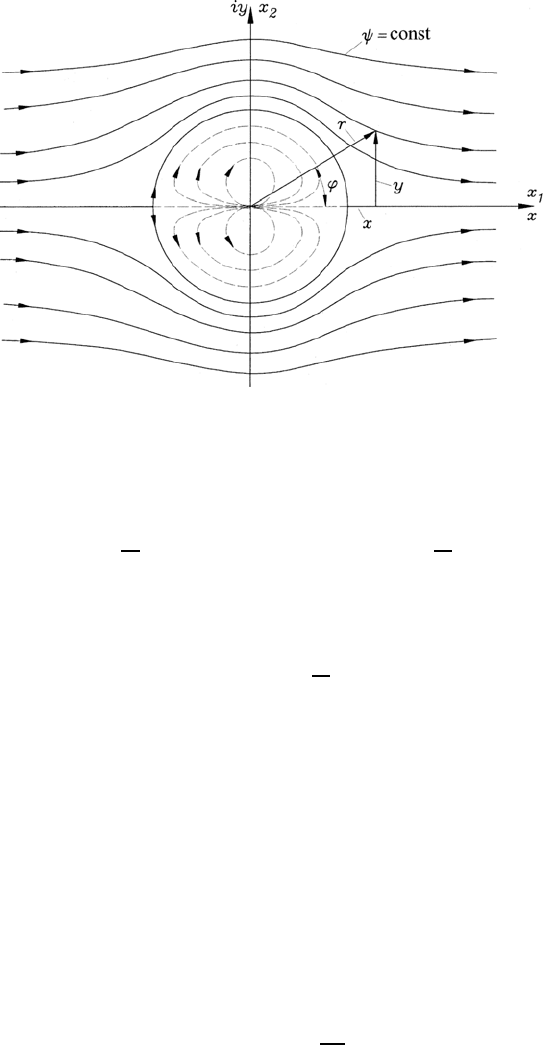
294 10 Potential Flows

Fig. 10.11 Flow lines of the ﬂow around a cylinder

For the potential and stream functions the following relationships can thus

be found:

Φ(r, ϕ)=



r +



cos ϕ and Ψ(r, ϕ)=



r −



sin ϕ. (10.83)

When one now inserts the radius r = R of a cylinder, the stream function

along a cylinder wall results as

Ψ(r, ϕ)=



R −



sin ϕ. (10.84)

When choosing the strength of the dipole-generated ﬂow D = U

,one

obtains for the stream function Ψ = 0 along the cylinder wall (r = R for all ϕ).

The resulting stream lines of this ﬂow are shown in Fig. 10.11. From this

representation, it can be seen that the stream line representing the cylinder

wall is a dividing line between an internal ﬂow caused by the dipole-generated

ﬂow and an external ﬂow coming from the ﬂow parallel to the x-axis. We

thus have an external ﬂow that can be interpreted as the ﬂow resulting from

two-dimensional considerations of the ﬂow of an incompressible viscosity-free

ﬂuid around a cylinder. When one takes into consideration the relationship

D = U

, derived for the strength of the dipole-generated ﬂow, for the

complex potential of the ﬂow around a cylinder with r ≥ R, the following

ﬁnal equation can be given:

F (z)=U



z +



. (10.85)

10.7 Potential Flow Around a Cylinder 295

In addition, for the potential and stream functions the following

relationships hold:

Φ(r, ϕ)=U



r +



cos ϕ and Ψ(r, ϕ)=U



r −



sin ϕ.

(10.86)

For the complex velocity, one can derive:

w(z)=

dF (z)

= U



1 −



= U



1 −

(−i2ϕ)



. (10.87)

Further conversions yield:

w(z)=U



(iϕ)

−

(−iϕ)



(−iϕ)

(10.88)

= U



(cos ϕ + i sin ϕ) −

(cos ϕ − i sin ϕ)



(−iϕ)

and lead to the following velocity components:

= U



1 −



cos ϕ and U

= −U





sin ϕ. (10.89)

Fortheoutercylinderarea(r = R)oneobtainsU

= 0; along the actual

cylinder there is only a ﬂow along the cylinder wall. For the latter a velocity

component results:

= −2U

sin ϕ for r = R. (10.90)

For ϕ =

, a velocity component therefore exists which is equal to twice

the value of the velocity parallel to the x-axis.

The indicated potential ﬂow around a cylinder results in a solution having

outﬂow conditions which are equal to the inﬂow conditions, so that no force

resulting from the ﬂow acts on the cylinder. This can also be derived from

the solution for the velocity ﬁeld itself. As concerns the quantity of the U

component, there exists a symmetry to the x-axis, so that the pressure distri-

bution is also symmetrical and therefore no resulting buoyancy force comes

about. Because of a likewise existing symmetry of the pressure distribution

to the y-axis, no resulting resistance force is produced either. As this result

is contradictory to our experience (d’Alambert’s paradox), this investigation

shows clearly the signiﬁcance of the viscosity terms in the basic equations of

ﬂuid mechanics. When these terms are not considered in ﬂuid-technical con-

siderations, for obtaining relevant information with regard to ﬂuid physics,

ﬂuid forces on bodies can only be dealt with to a limited extent.

296 10 Potential Flows

10.8 Flow Around a Cylinder with Circulation

In the previous section, the potential functions of the two potential ﬂows were

added to yield a new ﬂow. Determing the strength of the dipole-generated

ﬂow, the ﬂow around a circular cylinder resulted. In a similar way, one can

add complex potentials to give the following complex potential:

F (z)=U



z +



iΓ

2π

ln z + Ci. (10.91)

This complex potential results from the summation of the complex po-

tential of the ﬂow around a cylinder and the complex potential of a vortex,

where the centers of both ﬂows lie at the origin of the coordinate system.

The constant C was included in the above equation to be able to choose the

quantity of the stream function again in such a way that Ψ =0whenr = R,

i.e. the outer cylinder is to represent the ﬂow line Ψ = 0 in the ﬁnally derived

relation. For determining now the constant C, we insert in the above equation

z = re

(iϕ)

F (z)=U



(iϕ)

(−iϕ)

iΓ

2π

ln(re

(iϕ)

)



+ Ci. (10.92)

Making use of the relation e

iϕ

=cosϕ + i sin ϕ we obtain

F (z)=U



r +



cos ϕ + i



r −



sin ϕ



−

2π

ϕ + i

2π

ln r + Ci

(10.93)

from which one can deduce the following relationship for the potential and

stream functions:

Φ(r, ϕ)=U



r +



cos ϕ −

2π

ϕ, (10.94)

and

Ψ(r, ϕ)=U



r −



sin ϕ +

2π

ln r + C. (10.95)

In order to obtain Ψ =0forr = R and for all values of ϕ, one has to

choose the constant C = −

2π

ln R. In this way, for the complex potential

of the ﬂow around a cylinder with circulation the following complex potential

results:

F (z)=U



z +



+ i

2π

. (10.96)

This potential describes the plane ﬂow parallel to the x-axis, made up of

a dipole-generated ﬂow and a potential vortex located at the origin of the

coordinate system. For this ﬂow, the potential and stream functions can be

10.8 Flow Around a Cylinder with Circulation 297

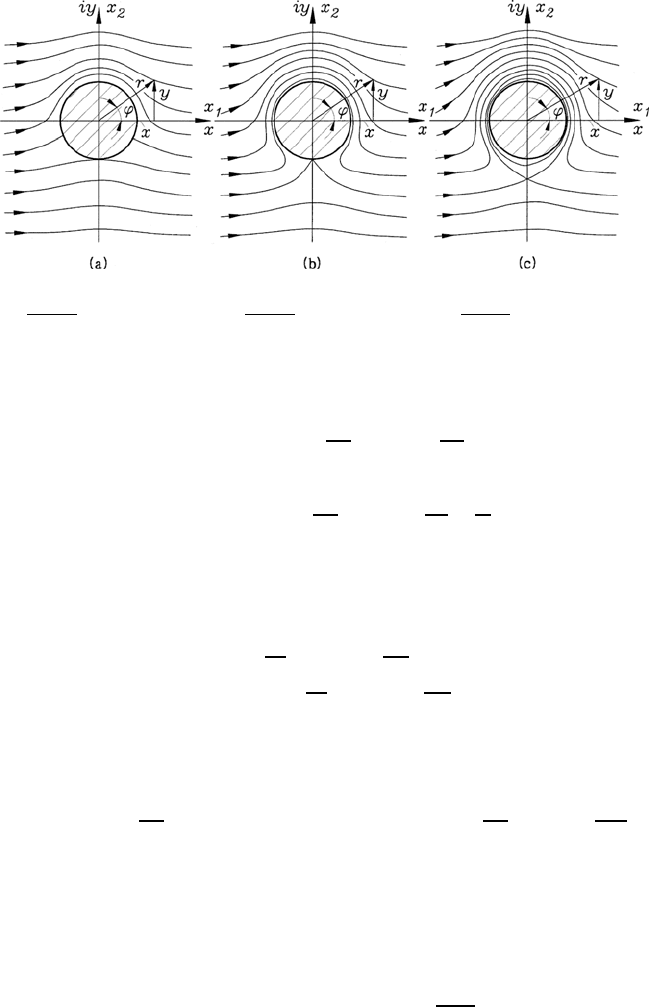
Fig. 10.12 Stream lines for the ﬂow around a cylinder with rotation: (a) circulation

0 ≤

4πU

< 1; (b) circulation

4πU

=1;(c) circulation

4πU

> 1

stated as follows:

Φ(r, ϕ)=U



r +



cos ϕ −

2π

ϕ.

Ψ(r, ϕ)=U



r −



sin ϕ +

2π

. (10.97)

The corresponding ﬂow and equipotential lines are shown in Fig. 10.12 for

three typical domains of the normalized circulation. The velocity components

of the ﬂow ﬁeld can be computed with the help of the complex velocity:

w(z)=U



1 −

(−i2ϕ)



iΓ

2πr

(−iϕ)





(iϕ)

−

(−iϕ)



+ i

2πr



(−iϕ)

(10.98)

By comparing this relationship with (10.31), the following velocity

components result:

= U



1 −



cos ϕ and U

= −U





sin ϕ −

2πr

(10.99)

For Γ = 0 the equations given in Sect. 10.7, resulting for the potential ﬂow

around a cylinder without circulation, can be deduced from (10.99).

By setting r = R in the above relationship, one obtains the velocity

components U

and U

along the circumferential area of the cylinder:

=0 and U

= −2U

sin ϕ −

2πR

. (10.100)

As expected, the stream line Ψ = 0 fulﬁls the boundary condition employed

with all potential ﬂows for solid boundaries. The U

component of the velocity

298 10 Potential Flows

has ﬁnite values along the cylinder surface. However, a stagnation point forms

in which also U

= 0. These are the stagnation points of the ﬂow with

positions on the surface of the cylinder. These locations are obtained from

(10.100) for U

=0.

It should be noted that the position of the stagnation points on the cylinder

surface are only given for Γ ≤ 4πU

R.ForΓ = 0 the stagnation points are

located at ϕ

=0andϕ

= π, i.e. on the x-axis. For ﬁnite Γ values in the

range 0 <Γ/(4πU

R) < 1, ϕ

is computed as negative, so that the stagnation

points come to lie in the third and fourth quadrants of the cylinder area, as

shown in Fig. 10.12. For Γ/(4πU

R) = 1, the stagnation points are located

in the lowest point of the cylinder surface area. For this location, ϕ

= −

and

2π

is computed (see Fig. 10.12).

When the circulation of the ﬂow is increased further, so that Γ>4πU

holds, stagnation points of the ﬂow cannot form any more along the cylinder

surface area. The formation of a “free stagnation point” in the ﬂow ﬁeld comes

about. The position of this point for U

=0andU

= 0 can be computed

from the above equations for the velocity components, i.e. from:



1 −



cos ϕ

=0, (10.101)

and





sin ϕ

= −

2πr

. (10.102)

As r

= R, i.e. the formation of the free stagnation point on the circum-

ferential area is excluded, the ﬁrst of the above two equations can only be

fulﬁlled for ϕ

2π

. Hence the second conditional equation for the

position coordinate of the “free stagnation point” is:





= ±

2πr

. (10.103)

As Γ>0 can be assumed in the above equation, and as the left-hand side

of the equation can only adopt positive values, only the positive sign of the

above equation yields values consistent with the ﬂow ﬁeld, i.e. the conditional

equation for r

reads:





2πr

, (10.104)

or rewritten in the following form to compute r

−

2πU

+ R

=0. (10.105)

As a solution of this equation, one obtains:

4πU



4πU



− R

. (10.106)