Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

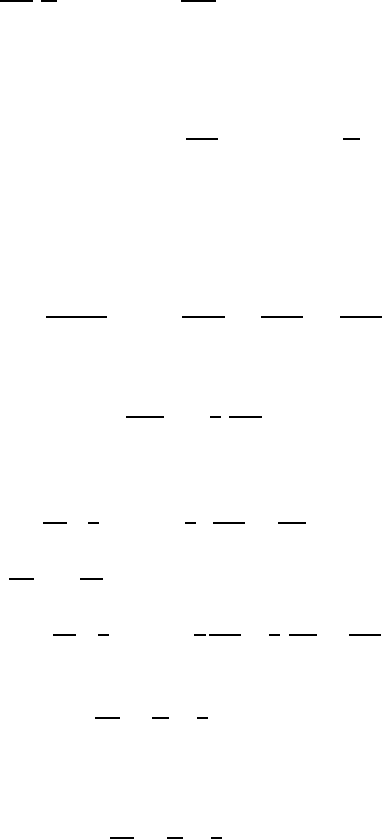
11.3 Transversal Waves: Surface Waves 319

This equation can now be interpreted, with Π =

P dt, as the pressure

impulse during the time interval τ. For small time intervals τ and for ρ =

constant the following results:

= −

∂

∂x

with

∂U

∂x

dt ≈ 0and

dt ≈ 0. (11.44)

Hence the ﬂuid motion generated as a result of pressure impulses on free

surfaces is described by a velocity potential. By setting

= U

= −

∂φ

∂x

with φ =

. (11.45)

The motion is therefore irrotational. Strictly, all this holds only at the free

surface and the determination of φ in the entire ﬂow area requires further

considerations.

The continuity equation can be written in terms of φ:

∂

∂x

=0=

∂

∂x

∂

∂x

∂

∂x

. (11.46)

The momentum (11.42) can be written as:

= −

∂P

∂x

+ g

(11.47)

and can be rewritten, after multiplication of the equation by U

, as follows:





= −



−

∂P

∂t



+ g

. (11.48)

With g

= −ρ

for

∂G

∂t

= 0 (see (5.57) and (5.58)), we obtain:





= −

−

∂P

∂t

−

(11.49)

or, rewritten:

∂φ

∂t

+ G = F (t). (11.50)

The function F(t) introduced by the integration can be included in the

potential φ, so that the ﬁnal relationship is:

∂φ

∂t

+ G =0. (11.51)

320 11 Wave Motions in Non-Viscous Fluids

Fig. 11.5 Two-dimensional surface wave

Figure 11.5 represents a two-dimensional surface wave whose deﬂection,

measured from the position of rest x

= 0, can be expressed as follows:

= y = η(x

,t)=η(x, t).

The kinematic boundary condition of the ﬂow problem to be solved can

therefore be stated as follows:

y = η(x, t)=0. (11.52)

This means that a ﬂuid particle which belonged to the ﬂuid surface at an

instant in time, will always belong to the free surface. From (11.52), the

following results, with u

as ﬂuid velocity of the considered wave motion:

(y −η)=0=

∂

∂t

(y −η)+u

∂

∂x

(y −η) = 0 (11.53)

or after diﬀerentiation:

−

∂η

∂t

− u

∂η

∂x

+ u

− u

∂η

∂x

=0. (11.54)

On now introducing the potential function φ, for which the following

relationship holds:

∂φ

∂x

∂φ

∂x

and u

∂φ

∂x

(11.55)

one obtains for the free surface with x

= x, x

= y and x

= z:

∂φ

∂y

∂η

∂t

∂φ

∂x

∂η

∂x

∂φ

∂z

∂η

∂z

. (11.56)

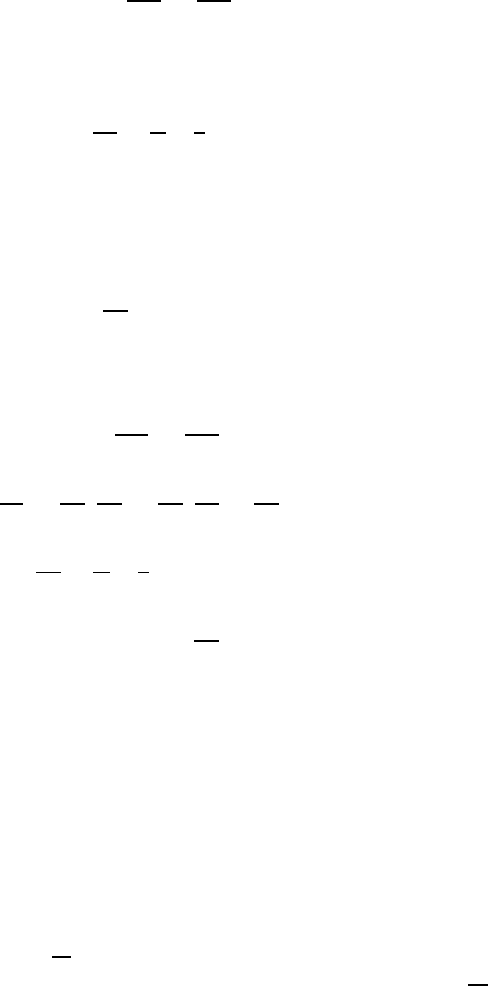
11.3 Transversal Waves: Surface Waves 321

In the entire area of the ﬂow, the potential function fulﬁls the continuity

equation, which can be stated in its two-dimensional form as follows:

∂

∂x

∂

∂y

=0. (11.57)

Under the assumption of absence of viscosity, the Bernoulli equation can be

employedintheformindicatedby(11.51).Hencewecanwrite:

∂φ

∂t

+ G =0. (11.58)

This equation is equivalent to the assumption that typically the pressure

along a free surface is constant and corresponds to the atmospheric pressure

over the surface. If one now includes in the considerations the solid bottom

in a certain position y = −h, one obtains as a boundary condition at this

distance

∂φ

∂y

=0 for y = −h. (11.59)

Hence one can write the following set of equations, which are to be fulﬁlled

in order to treat the propagation of waves on free surfaces analytically:

∂

∂x

∂

∂y

∂η

∂t

∂φ

∂x

∂η

∂x

∂φ

∂z

∂η

∂z

∂φ

∂y

for y = η

∂φ

∂t

+ gη =0 fory = η

∂φ

∂y

=0 fory = −h.

(11.60)

Here the last equations are to be understood as boundary conditions. Hence

it becomes clear that the problem, when solving wave problems for ﬂuids with

free surfaces, is heavily determined by the imposed kinematic and dynamic

boundary conditions. It proves to be a peculiarity of the treatment of wave

motion in ﬂuids with free surfaces that the main problem is the introduction

of the boundary conditions and not the solution of the diﬀerential equations

describing the ﬂuid motion.

Considerable simpliﬁcations of the system of equations result from the

assumption of surface waves of small amplitudes. Assuming that the ampli-

tude of the wave is smaller than all other linear dimensions of the problem,

i.e. smaller than the depth of the water h and the wavelength λ,itresults

that η is small and

∂η

∂x

also can be assumed to be small. The latter is the

gradient of the shape of the water surface. Moreover, it holds that

∂φ

∂x

can

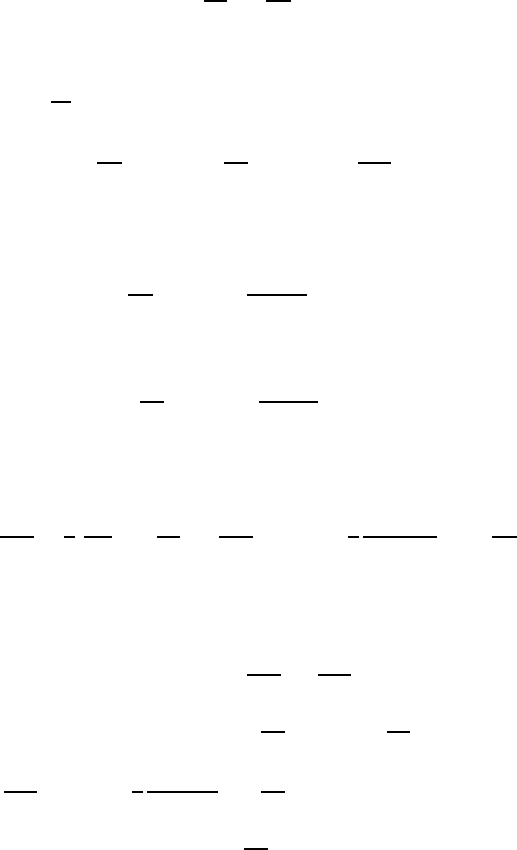
322 11 Wave Motions in Non-Viscous Fluids

also be assumed to be small. Surface waves have no high frequencies and the

assumption of small amplitudes is also valid for their propagation. Thus, for

two-dimensional waves we can write:

∂η

∂t

∂φ

∂η

for y = η. (11.61)

This equation still contains the problem that the boundary condition, applied

for surface waves, has to be imposed at the point y = η. However, when one

expands

∂φ

∂η

in a Taylor series:

∂φ

∂y

(x, η, t)=

∂φ

∂y

(x, 0,t)+η

∂

∂η

(x, 0,t)+··· (11.62)

it can be seen that the second term on the right-hand side can be neglected

because of the assumed small η values. In an analogous way, we can write:

∂φ

∂t

(x, η, t)+

P (x, t)

+ g · η(x, t)=F (t) (11.63)

and for small velocities the following relation is valid:

∂φ

∂t

(x, 0,t)+

P (x, t)

+ g · η(x, t)=0, (11.64)

where the function F(t) was included in the potential φ(x, y, z).

Diﬀerentiation of (11.64) with respect to t yields:

∂

∂t

∂P

∂t

+ g

∂η

∂t

∂

∂t

(x, 0,z)+

∂P(x, z)

∂t

+ g ·

∂φ

∂y

(x, 0,z)=0

(11.65)

so that one obtains the following simpliﬁed set of equations for the treatment

of surface waves of small amplitudes:

∂

∂x

∂

∂y

∂φ

∂y

(x, 0,t)=

∂η

∂t

(x, t)(fory = η)

∂

∂t

(x, 0,t)+

∂P(x, t)

∂t

+ g

∂φ

∂y

(x, 0,t)=0 (fory = η)

∂φ

∂y

(x, −h, t)=0 (fory = −h).

(11.66)

With the above equations, gravitational waves and capillary waves can be

treated, which usually represent waves with small amplitudes.

11.4 Plane Standing Waves 323

11.4 Plane Standing Waves

When considering wave motions, where the ﬂuid particles move only parallel

to the x

−x

plane, i.e. where the pressure P and the velocity U

are inde-

pendent of x

, so that the ﬂuid motions in all areas parallel to the x

− x

plane take place in the same way, a plane wave motion with the following

potential results:

φ(x, y, t)=φ(x, y)cos(ϕt + ). (11.67)

For the case of a standing wave to be dealt with in this section, it can be

stated that:

φ(x, y)=

P (y)

sin [k(x − ξ)]. (11.68)

The potential φ fulﬁls the Laplace equation:

∂

∂x

∂

∂y

=0. (11.69)

With ρ

∂

∂x

= −P (y)k

sin[k(x − ξ)] and ρ

∂

∂y

= P

sin[k(x − ξ)], one

obtains the following diﬀerential equation:

− k

P = 0 (11.70)

the solution of which is:

P (y)=C

exp(ky)+C

exp(−ky). (11.71)

From more precise considerations, the integration constant C

,resultsas

= 0, as otherwise for large depths y =→−∞the P (y) term would become

very large, so that the solution:

φ(x, y)=

exp(ky)sin[k(x − ξ)] (11.72)

can be obtained, or:

φ(x, y, t)=

exp(ky)sin[k(x − ξ)] cos(ϕt + ). (11.73)

By starting from the assumption that the occurring ﬂuid motion is slow,

the equation:

∂φ

∂t

+ gη =0 fory = η (11.74)

can be written as follows:

∂φ

∂t

+ gη =0 fory = η. (11.75)

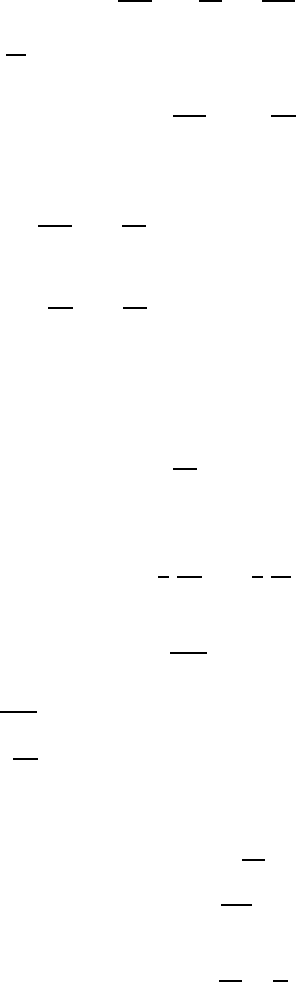
324 11 Wave Motions in Non-Viscous Fluids

Diﬀerentiation with respect to time yields the diﬀerential equation indicated

below, as the pressure along the free surface does not change:

∂

∂t

+ g

∂η

∂t

∂

∂t

+ gu

. (11.76)

With u

∂φ

∂y

, one can ﬁnally write:

∂

∂t

= −g

∂φ

∂y

. (11.77)

Employing (11.77) to treat (11.73), one obtains:

∂

∂t

= −

exp(ky)sin[k(x − ξ)]ϕ

cos(ϕ + ) (11.78)

and

∂φ

∂y

k exp(ky)sin[k(x − ξ)] cos(ϕ + ) (11.79)

= kg. (11.80)

Hence, for the remaining considerations, the following ﬂuid motion has to be

examined, which, for the sake of simplicity, is considered for ξ =0and =0:

φ(x, y, t)=

exp(ky)sin(kx)cos(εt). (11.81)

For the free surface one can compute from (11.75):

η = −

∂φ

∂t

= −

∂

∂t

φ(x, 0,t) (11.82)

η =

sin(kx)sin(ϕt). (11.83)

With A =

ρg

sin(ϕt)itholdsthatη = A sin(kx).

For x =

mπ

,form =0, ±1, ±2, ±···, nodal points of a standing wave

result. In the middle between these nodes are the “antinodal points” of the

wave motion. The wavelength of the sinusoidal ﬂuid motion can be computed

as:

λ =

2π

. (11.84)

The amplitude of the wave motion is

sin(ϕt)=A, where for the frequency

of the wave motion the following holds:

f =

2π

. (11.85)

11.5 Plane Progressing Waves 325

Taking into consideration (11.80), (11.84) and (11.85), one obtains

T =

2πk

or λ =

gτ

2π

(11.86)

λ =

2πf

. (11.87)

The above relationships show that the wavelength of standing ﬂuid waves

decreases with increasing frequency of the motion.

11.5 Plane Progressing Waves

For the derivations given below, it is assumed that the ﬂuid considered takes

up the space as follows (see Fig. 11.6) for the x −y coordinate arrangements:

−∞ ≤ y ≤ 0and −∞≤x ≤ +∞

and the ﬂuid is assumed, at the point y = 0, to occupy a free surface. For

the considerations carried out it represents a ﬁnite surface. The equations

required for the treatment of progressing waves can be stated as follows:

∂

∂x

∂

∂y

=0. (11.88)

With y = η(x

,t) for the free surface it holds that

(y −η)=0 ; u



∂

∂t

+ u

∂

∂x



η. (11.89)

Neglecting the term of second order, the following equation results:

∂φ

∂y

∂η

∂t

. (11.90)

for

and

Fig. 11.6 Illustration of the decrease for y →−∞

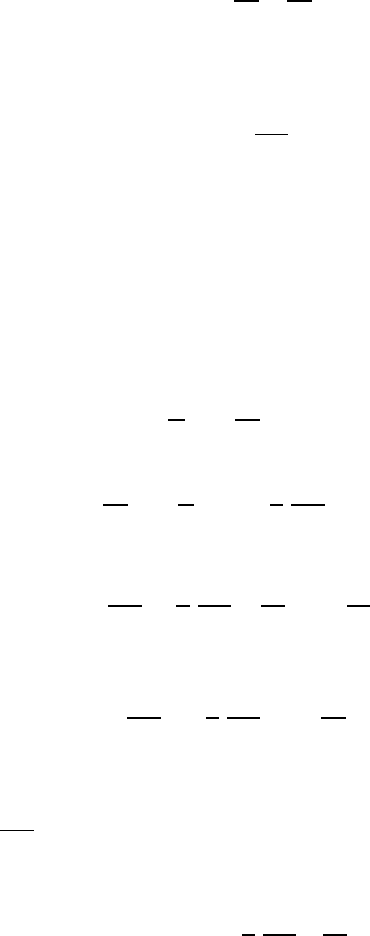
326 11 Wave Motions in Non-Viscous Fluids

For the pressure at the free surface it can be stated that:

P = −σ





, (11.91)

where R

and R

represent the main radii of curvature of the free surface

and σ is the surface tension. Linearized, this relationship can be written as:

P = −σ

∂

∂x

, (11.92)

where the pressure above the free surface is taken to be P =0,otherwiseP

is to be replaced by P = P

For plane progressing waves, the following potential can be stated:

φ(x, y, t)=C exp(ky)cos[k (x − ct)] (11.93)

with φ =0fory = −∞. The formulation for φ(x, y, z) fulﬁls the continuity

equation in the form of (11.69).

The Bernoulli equation can be stated as follows:

= −

∂φ

∂t

− gy (11.94)

or rewritten:

∂φ

∂t

= −

− gη =

∂

∂x

− gη. (11.95)

From this, the following relationship results:

∂

∂t

∂

∂x



∂η

∂t



− g

∂η

∂t

(11.96)

and with consideration of equations (11.90), (11.95) can be written as:

∂

∂t



∂

∂x

− g



∂φ

∂g

. (11.97)

For the left-hand side of (11.95), one can write using (11.93):

∂

∂t

= −Ck

exp(ky)cos[k(x − ct)] = −k

φ (11.98)

so that the following holds:

φ =



g −

∂

∂x



∂φ

∂y

. (11.99)

11.5 Plane Progressing Waves 327

With

∂φ

∂y

= kφ and

∂

∂x

= −k

φ, the following relationship results from

(11.99) for the velocity of the progressing wave:

kσ

. (11.100)

With k =

2π

, it can be seen that for long waves the inﬂuence of gravity

dominates:

c =

shear waves. (11.101)

For waves with small wavelengths, the capillary eﬀects dominate:

c =

kσ

capillary waves. (11.102)

Concerning wavelengths, often the path lines of the ﬂuid particles are also of

interest, which occur close to the water surface or at certain depths below

the water surface. In this respect, the following can be carried out, where x

and y

are introduced as the coordinates which, with the help of:

∂φ

∂x

= Ck exp(ky)sin[k(x − ct)] (11.103)

∂φ

∂y

= Ck exp(ky)cos[k(x − ct)] (11.104)

fulﬁl the following equations:

x = x

+ C · k exp(ky)cos[k(x − ct)]





(11.105)

y = y

+ ck exp(ky)sin[k(x − ct)]



−1



(11.106)

or rewritten:

(x − x

)

+(y − y

)





exp(2ky

). (11.107)

The path lines of the ﬂuid particles are derived as circles whose radii become

smaller with increasing water depth. For the water surface, the radius of the

circular path is equal to the amplitude of the surface wave, while at a certain

depth it has already decreased to 1/535th of the wave amplitude at the water

surface. This makes it clear that the considered wave motion of ﬂuid particles

remains limited to an area in the immediate proximity of the water surface.

Figure 11.7 shows the circular paths described by ﬂuid particles. These

will run in an anticlockwise direction, so that the following expressions for

the x and y motion holds:

328 11 Wave Motions in Non-Viscous Fluids

Fig. 11.7 Circular paths of ﬂuid particle motion

Fig. 11.8 Path lines in a plane gravity wave

(x − x

)=a exp(ky

)sinΘ (11.108)

(y −y

)=−a exp(ky

)cosΘ. (11.109)

HencewecanwriteforΘ:

Θ = kx

+ kctcos(yt + ). (11.110)

The changes of the motions of the ﬂuid particles with water depth are

sketched in Fig. 11.8. The strong decrease of the radius of the circular ﬂuid

motion with depth was not taken into consideration in Fig. 11.7.

In order to be able to investigate gravity waves with free surfaces in ﬂuids

with a ﬁnite depth h, a mean surface position at point y = 0 is assumed. At

position y = −h a wall is considered as being given, so that a mean ﬂuid ﬁlm

thickness with height h occurs. To fulﬁll now the continuity equation:

∂

∂x

∂

∂y

= 0 (11.111)