Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

10.9 Summary of Important Potential Flows 299

With this the position coordinates of the free stagnation point result as:

3π

and

4πU

⎡

⎣

1 −



4πU



⎤

⎦

. (10.107)

The negative sign of the root in the solution for r

wasomittedinthe

statement of the position coordinates for the free stagnation point, as this

would lead to a radius which is located inside the cylinder surface area. As

only the ﬂow around the cylinder is of concern, this second solution of the

square equation for r

is of no interest in the considerations presented here.

Moreover, it was also excluded from the solution for the position coordi-

nates of the free stagnation point that the angle ϕ

also has a solution for

. The reason for this is that for

4πU

= 1 the stagnation point appears

as a solution only in the lower half of the cylinder surface area. Inclusion

of the solution for ϕ

would mean that a small increase in the circu-

lation, to an extent that the standardized circulation is given a value larger

than 1, would lead to a jump of the stagnation point from the lower to the

upper half of the ﬂow. Considerations on the stability of the position of the

stagnation points show, however, that only the lower stagnation point, i.e

3π

, can exist as a stable solution. Because of the superposition of the

ﬂow around a cylinder with a potential vortex, a ﬂow ﬁeld has come about,

which again is symmetrical concerning the y-axis. With this outcome of the

above considerations it is in turn determined that, owing to the ﬂow around

the cylinder, the cylinder surface area obtains no resulting force acting in the

ﬂow direction, i.e. no resistance force occurs because of the ﬂow. Owing to

the imposed circulation, an asymmetric ﬂow with respect to the x-axis, has

come about, however, and this leads to a buoyancy force, i.e. to a resulting

force on the cylinder, directed upwards. As the velocity component on the

upper side of the cylinder is larger than that on the lower side, because of

the Bernoulli equation a pressure diﬀerence results, with low pressure on the

upper side. This causes a ﬂow force directed upwards. The quantitative deter-

mination of this force requires integral relationships to be applied as derived

in Sect. 10.10.

10.9 Summary of Important Potential Flows

In the preceding sections, a number of potential ﬂows were discussed which

are known as basic potential ﬂows and whose treatment give an insight into

the ﬂuid ﬂow processes that occur. In Table 10.1, further analytical functions

are stated, in addition to the already extensively discussed examples, which

can be used for the derivation of potential and stream functions and the

corresponding velocity ﬁelds of potential ﬂows. By equating the indicated

300 10 Potential Flows

Table 10.1 Examples of complex functions, potentials φ and stream functions ψ for two-dimensional potential ﬂows

Complexes potential Potential Stream function Velocity Stream lines

F (z) Φ(x, y) Ψ (x, y) uv c Ψ=const

∞

− iv

∞

)zu

∞

x + v

∞

y − v

∞



∞

+ v

∞

Parallel ﬂow

Parallel ﬂow u

∞

0 u

∞

z in

x-direction

Stagnation

− y

) axy ax −ay ar

point a real > 0

2π

ln z Source

Q>0,

2π

ln r =

2π

ϕ =

2π

arctan

2π

2πr

Sink

Q<0

2π



+ y

Vortex

2π

i ln z −

2π

arctan

2π



+ y

2π

−

2π

2πr

Γ > 0 turning right

Γ < 0 turning left

10.9 Summary of Important Potential Flows 301

Dipole

−

−x

)

−m

2xy

)

−

∞

z +

ln zu

∞

x +

2π

ln ru

∞

y +

2π

ϕu

∞

2π

Parallel ﬂow

+ Source/Sink

Parallel ﬂow On the cylinder

+Dipole u

∞





∞



1 −



∞

sin

ϕ −2u

∞

sin ϕ cos ϕ 2u

∞

sin ϕ

∞



z +



∞



z +



2π

i ln z

Flow around cylinder u

∞





∞



1 −



∞

sin

ϕ −2u

∞

sin ϕ cos ϕ 2u

∞

sin ϕ +

2πR

+Vortex −

2π

ϕ +

2π

ln r +

2πR

sin ϕ −

2πR

cos ϕ

Flow around cylinder u

∞

x +

2π

ϕu

∞

y +

2π

ln ru

∞

2π

−

2π

+Vortex

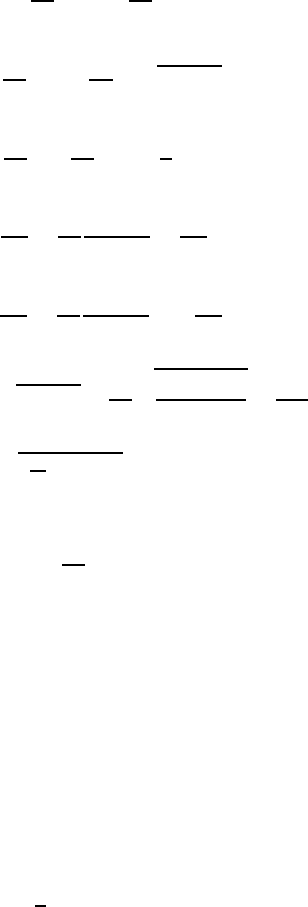
302 10 Potential Flows

potential or stream-function values to a constant, the equipotential or ﬂow

lines of the potential ﬂow can be stated.

The procedure concerning the derivations of ﬂuid-mechanically interesting

quantities will be represented here once again brieﬂy with the aid of the

source-sink ﬂow taken from the table.

Example: F (z)=

2π

· ln z =

2π

(ln r + iϕ); z = x + iy = re

iϕ

Potential: Φ =

2π

ln r =

2π



+ y

Stream function: Ψ =

2π

ϕ =

2π

arctan

Velo city: u =

∂Φ

∂x

2π

+ y

∂Ψ

∂y

v =

∂Φ

∂y

2π

+ y

= −

∂Ψ

∂x

c =



+ v

2π

+ y

)

2πr

Equipotential lines: y =



2π

·K

− x

Φ = K

Stream lines: y = x tan



2π



Ψ = K

10.10 Flow Forces on Bodies

In Sects. 10.1 and 10.2 the possibility was already mentioned of computing

from the pressure distribution along a body contour the forces acting on

bodies that are caused by potential ﬂows. When one has determined the

velocity ﬁeld of a potential ﬂow according to the preceding sections, the

velocity distribution is also known along the body contour. This contour

represents a ﬂow line of the ﬂow ﬁeld (as the reader will hopefully remember).

In each point of the ﬂow holds the Bernoulli equation in the following form:

P +

+ U

)=constant. (10.108)

10.10 Flow Forces on Bodies 303

For the stream line Ψ = 0 and thus the body contour, U

= 0 holds, i.e.

P +

= constant. (10.109)

The quantity U

can be computed from U

and U

or from U

and U

follows:

= U

+ U

= U

+ U

. (10.110)

Along the contour of a ﬂow body, the following integrations can be carried

out:

= −

(

P cos ϕds = −

(

P dx

and F

= −

(

P sin ϕds = −

(

P dx

(10.111)

in order to conserve the ﬂow forces in the x

or the x

direction of a Cartesian

coordinate system (here ϕ is the angle between body contour and x

-axis).

On referring the directions of the forces to the inﬂow direction and choosing

the latter such that it is identical with the x

direction, F

results in the

resisting force on the body, while F

yields the buoyancy force.

In the present section, an attempt is made to derive the forces di-

rectly through appropriate equations which use the complex velocity. To

carry out the necessary derivations, a control volume around the ﬂow body

is taken with the height 1 vertical to the plane of ﬂow, as indicated in

Fig. 10.13.

In this way, a control volume comes about which is determined by an

internal and an external contour. The ﬂuid forces attacking in the center of

gravity of the submerged body and given in the directions of the x

-and

-axis, respectively, are likewise indicated in Fig. 10.13. Also sketched is the

moment which a body can experience by the ﬂow forces that occur.

When now applying to the control volume, indicated in Fig. 10.13, the

momentum equations in integral form, as they were treated in Chap. 8,

Fig. 10.13 Fluid element and surrounding control volume

304 10 Potential Flows

the consideration can be expressed in words that the increase of x

or x

momentum of the ﬂow can only be caused by the ﬂow forces acting on the

body in the x

or x

direction. In the x

direction the following force results:

−F

−

(

P dx

(

ρU

− U

). (10.112)

This relationship considers that the internal contour of the control volume

represents the surface of an emerged body, so that the ﬂuid does not ﬂow

through it. The pressure forces acting on the internal contour C

in the x

direction were combined into the resulting force F

. The force acts in the

positive direction on the body and thus in the negative direction on the ﬂuid;

this explains the negative sign in front of F

A similar relationship can be written for the x

direction:

−F

(

P dx

(

ρU

− U

). (10.113)

By integrating the two equations in terms of the forces and solving them,

one obtains

(

−(P + ρU

)dx

+ ρU

, (10.114)

and

(

(P + ρU

)dx

− ρU

. (10.115)

Applying the Bernoulli equation:

P +

+ U

)=constant, (10.116)

and taking into consideration that the line integrals

)

(constant)dx

and

)

(constant)dx

are both equal to zero along a closed contour of the control

volume, one obtains for the forces in the x

and x

directions the following

terms:

= ρ

(



−

− U

)dx



, (10.117)

= −ρ

(



− U

)dx



Considering the quantity:

(

(z)dz = i

(

− iU

)

(dx + idy) (10.118)

10.10 Flow Forces on Bodies 305

one obtains:

(

(z)dz = ρ

(



−

− U

)dx



+ i



− U

)dx



. (10.119)

This equation shows that the ﬂow forces in the x

and x

directions that

act on a body can be computed as follows:

(

(z)dz = F

− iF

. (10.120)

Through this relationship, the Blasius integral for ﬂow forces, the ﬂow

forces on bodies submerged in potential ﬂows can be computed easily.

Employing the above relationship to compute the resulting force com-

ponents on the cylinder with circulation, one obtains, beginning with the

complex potential:

F (z)=U



z +



+ i

2π

(10.121)

for the complex velocity:

w(z)=

dF (z)

= U



1 −



iΓ

2πz

. (10.122)

For w

(z), one can compute:

(z)=U

−

πz

−

ΓR

πz

−

4π

, (10.123)

or, rewritten:

(z)=U

−



4π



−i



ΓR

πz

−

πz



. (10.124)

Inserting this into the relationship for the components K

and K

of the

ﬂow force, given above, one obtains for the integration along the cylinder

surface area

− iF

= i

(

(z)dz = i

(



−



4π



−i



ΓR

πz

−

πz



dz (10.125)

On introducing into this integral z = re

(iϕ)

and considering that for the

cylinder surface area r = R holds, then integration can be carried out and

leads to the result:

− iF

= −iρU

Γ (10.126)

306 10 Potential Flows

Fig. 10.14 Determination of the direc-

tion of the buoyancy forces

or F

=0andF

= ρU

Γ . This is the Kutta–Joukowski equation for the

lift force. This equation indicates that the ﬂow force occurring through a

potential ﬂow around a cylinder is equal to zero, when there is no circulation.

When there is circulation present, no resisting force occurs but a buoyancy

force, which is proportional to the ﬂuid density, to the inﬂow velocity and

the circulation:

= ρU

Γ (10.127)

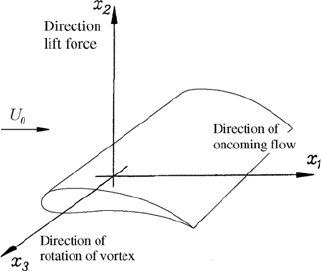
As the sign of this force is positive, there is a buoyancy force acting on

the cylinder. The rule holding for the direction of the bouyancy is stated in

Fig. 10.14. The inﬂow direction, the direction of rotation of the vortex and

the direction of the resulting buoyancy represent the directions of the axes

of a rectangular coordinate. Hence, the force orientation is that of the “right

hand rule”.

The positive force in the case of the ﬂow around a cylinder with circulation

comes about as a result of the mathematically positive direction of rotation

of the potential vortex at the origin of the coordinate system.

Flow forces acting on bodies can also lead to moments of rotation. There,

computation can again be carried out in a conventional way, i.e. by integration

of the moment contributions generated by pressure eﬀects on areas. When

again assuming the moment acting on the body to be positive, the following

equation holds for the moment acting on the ﬂuid:

M +

(

[Px

+ Px

+ ρU

− U

)

−ρU

− U

)] = 0

(10.128)

On solving in terms of M, one obtains:

M = −

(

+ Px

+ ρ(U

+ U

−U

− U

) ] (10.129)

References 307

By eliminating the pressure with the help of the Bernoulli equation:

P +

+ U

)=constant, (10.130)

and considering that the integrals are

)

(constant)x

)

(constant)

=0,oneobtains:

M =

(

− U

)(x

− x

)+2U

+ x

)

, (10.131)

and it can be shown that the following holds (second Blasius integral):

M =

⎛

⎝

(

(z)dz

⎞

⎠

. (10.132)

An evaluation of the integral yields:

M = Re

⎡

⎣

(

(x + iy)(U

− iU

)

(dx + idy)

⎤

⎦

, (10.133)

and considering that x

= x and x

= y,oneobtains:

M = Re {

(

− U

)(x

− x

)+2U

· (x

+ x

)

+ i

− U

)(x

+ x

) − 2U

− x

)

} (10.134)

The real part of (10.134) corresponds to the term (10.131), which was to

be proved.

On applying relation (10.131) to the ﬂow around a cylinder with

circulation, one obtains:

M = Re

⎡

⎣

(



z −

−

ΓR

πz

−

4π



⎤

⎦

(10.135)

On inserting z = re

(iϕ)

and r = R in (10.135), one obtains as a solution

M = 0. The ﬂow around a cylinder does not furnish a hydrostatic moment

on the cylinder, even when the ﬂow has circulation.

References

10.1. Yuan, S.W., Foundations of Fluid Mechanics. Mei Ya Publications, Taipei, 1967.

10.2. Allen, T. Jr., Ditsworth, R.L., Fluid Mechanics, McGraw-Hill, New York, 1972.

10.3. Schade, H., Kunz, E., Str¨omungslehre mit einer Einf¨uhrung in die Str¨omungsme

stechnik von Jorg-Dieter Vagt. 2, Auﬂage, Walter de Greyter, Berlin, 1989.

308 10 Potential Flows

10.4. Zierep, J., Grundz¨uge der Str¨omungslehre. 6. Auﬂage, Springer, Berlin,

Heidelberg, New York, 1997.

10.5. Siekmann, H.E., Str¨omungslehre f¨ur den Maschinenbau. Springer, Berlin,

Heidelberg, New York, 2001.

10.6. Spurk, J.H., Str¨omungslehre. 5. Auﬂage, Springer, Berlin, Heidelberg, New

York, 2004.