Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows
Подождите немного. Документ загружается.


8.5 Applications of the Integral Form of the Basic Equations 237
the following simplifications can be introduced:
∂
∂t
#
V
K
ρU
j
dV =0, stationary fluid flow problem
#
O
K
P dF
j
=0, constant pressure along the surface of the control volume
#
O
K
τ
ij
dF
i
=0, viscosity forces are neglected
#
O
K
ρg
j
dV =0, gravitation is neglected.
(8.72)
Hence the following simplified momentum equation results:
#
O
K
ρU
i
U
j
dA
i
=
F
j
. (8.73)
The force exerted on the fluid can be determined by the equation for the x
1
components of the total force
−ρUU (bH)+ρ(U cos α)U(εbH)=F
1
, (8.74)
F
1
= −ρU
2
bH(1 − ε cos α). (8.75)
The negative value of the force K
1
results from the fact that the force exerted
on the plate is computed.
From the equation for K
2
,oneobtains:
ρU(1 − )Hb(−U )+ρUεbH(U sin α)=0, (8.76)
and, hence, for K
2
= 0, the connection between the deflection angle α and
the ratio ε can be computed as
−ρU
2
bH [(1 − ε) − ε sin α]=0, (8.77)
ε =
1
1+sinα
. (8.78)
Hence the ratio of splitting the jet in Fig. 8.6 can be determined from the
deflection of the jet from the horizontal position, i.e. by measuring the
angle α.
8.5.6 Mixing Process in a Pipe of Constant
Cross-Section
In a pipe, two fluids flow at constant velocities U
A
,U
B
. These fluids mix with
one another as they move downstream in a channel Fig. 8.7. The pressure
at point 1 and the partial areas in which the velocities U
A
,U
B
hold, will be
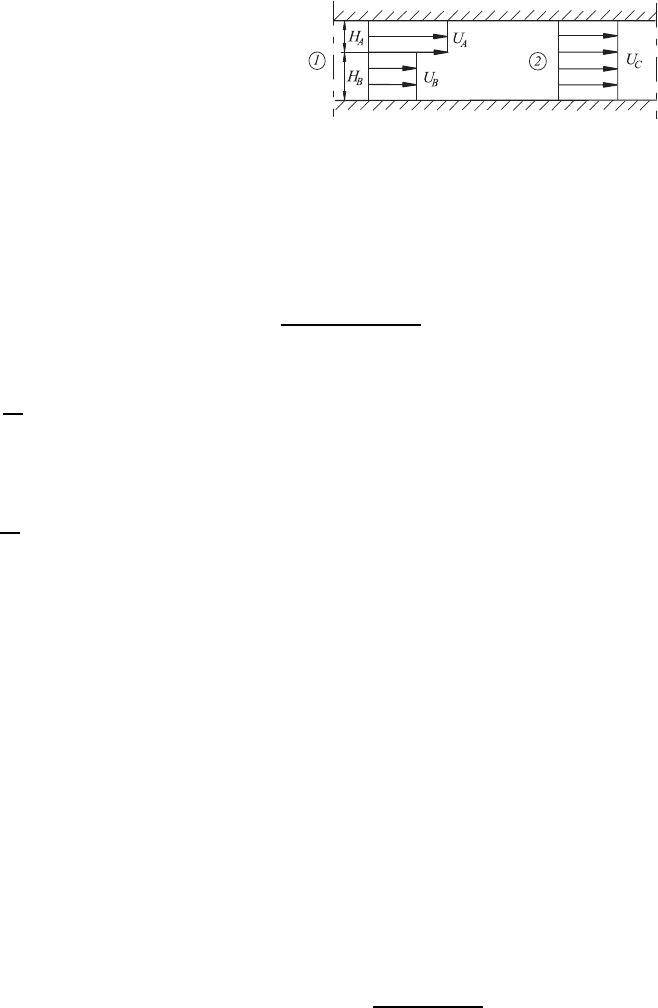
238 8 Integral Forms of the Basic Equations
Fig. 8.7 Diagram for explaining the
mixing process
given. Sought is the pressure P
2
at point 2 where a constant velocity
¯
U
C
over
the pipe cross-section has been reached.
From the integral form of the continuity equation, one obtains
b(−ρH
A
U
A
− ρH
B
U
B
+ ρ(H
A
+ H
B
)
¯
U
C
)=0, (8.79)
or, rearranged for
¯
U
C
,
¯
U
C
=
U
A
H
A
+ U
B
H
B
H
A
+ H
B
. (8.80)
The momentum equation:
∂
∂t
#
V
K
ρU
j
dV +
#
O
K
ρU
i
U
j
dA
i
= −
#
O
K
P dF
j
−
#
O
K
τ
ij
dA
i
+
#
V
K
ρg
j
dV +
F
j
(8.81)
can be simplified as follows:
∂
∂t
#
V
K
ρU
j
dV =0, stationary flow problem
#
O
K
τ
ij
dA
i
=0,µ= 0, i.e. the assumption of absence of viscosity is made
#
V
K
ρg
j
dV =0, no component of gravitation exists in horizontal direction
F
j
=0, no external forces act on the control volume.
(8.82)
From these simplifying assumptions it follows that
#
O
K
ρU
i
U
j
dA
i
= −
#
O
K
P dA
j
. (8.83)
For the present problem this results in:
−ρU
2
A
H
A
− ρU
2
B
H
B
+ ρ
¯
U
2
(H
A
+ H
B
)=(P
1
− P
2
)(H
A
+ H
B
). (8.84)
When one now inserts the above expression for
¯
U
c
and solves the equation
for P
2
,oneobtains:
P
2
= P
1
+ ρ(U
A
− U
B
)
2
H
A
H
B
(H
A
+ H
B
)
2
. (8.85)
The pressure therefore increases as a consequence of mixing the two flows
from position (1) to position (2).

8.5 Applications of the Integral Form of the Basic Equations 239
8.5.7 Force on a Turbine Blade in a Viscosity-Free
Fluid
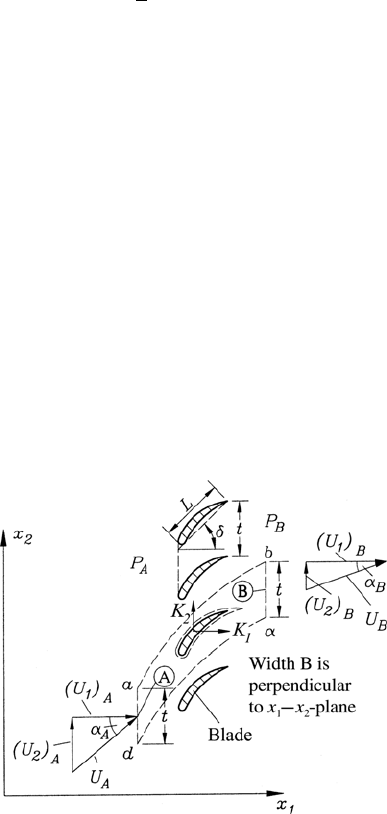
In flow machines, wheels with blades are used to exploit the momentum of
fluid flows for propulsion purposes, i.e. to drive the rotating wheels. A jet
from a rectangular nozzle (plane jet having a width H and depth b)hits
a stationary blade which deflects the jet symmetrically to two sides around
the angle 180
◦
- β (Fig. 8.8). The information on the inflowing and outflowing
fluid flows is given. The pressure along the surface of the marked control
volume is equal all over and can be assumed to be the ambient pressure, so
that the integral form of the momentum equation can be given as
∂
∂t
#
V
K
ρU
j
dV +
#
O
K
ρU
i
U
j
dA
i
= −
#
O
K
P dA
j
−
#
O
K
τ
ij
dA
i
+
#
V
K
ρg
j
dV +
F
j
. (8.86)
This equation can be simplified in the following way, if gravitation is
negligible:
∂
∂t
#
V
K
ρU
j
dV =0, stationary flow problem
#
O
K
P dA
j
=0, as P = P
0
along all surfaces of the control volume
#
O
K
τ
ij
dA
i
=0, as µ = 0 was set in the assumptions
#
V
K
ρg
j
dV =0, as gravitation is negligible.
(8.87)
Fig. 8.8 Diagram for explaining the force
on a turbine blade moving in the x
1
direction
240 8 Integral Forms of the Basic Equations
Hence the following final equation results:
#
O
K
ρU
i
U
j
dA
i
=
F
j
. (8.88)
As the problem is symmetrical, only the horizontal component j =1hasto
be considered, i.e. in the j = 2 direction no resultant force appears, so that
the conservation of momentum can be written as follows:
−ρHbU
2
+2
1
2
ρHbU (−U · cos β)=F
1
. (8.89)
The resultant force on the blade thus results in:
F
S
= −F
1
= ρHbU
2
(1 + cos β). (8.90)
This equation makes it clear that by deflecting the jets in direction of the
incoming flow, an increase in the force F
1
acting on the turbine blade can be
obtained.
8.5.8 Force on a Periodical Blade Grid
Assumptions: g =0,µ = 0 for the flow problem given below.
Two-dimensional grids of blades are used in flow machines in order to
exploit forces caused by flows to drive rotating wheels.
Figure 8.9 shows such a set of blades arranged periodically in the x
1
−x
2
plane. These blades are approached by a flowing fluid with an approach
Fig. 8.9 Diagram explaining the effect of blade grids
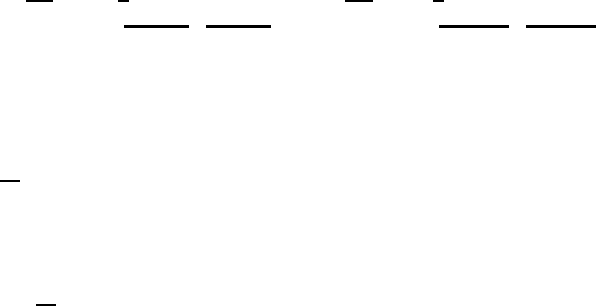
8.5 Applications of the Integral Form of the Basic Equations 241
velocity U
A
= {(U
1
)
A
, (U
2
)
A
, 0} comprising two components, i.e. the U
3
component of the oncoming flow field is assumpt to be zero. Because of the
deflection of the flow by the blade, the departing velocity differs from the
approach velocity, so that the following holds:
U
B
= {(U
1
)
B
, (U
2
)
B
, 0} = U
A
. (8.91)
The assumed features of U
A
and U
B
, for which it always holds that (U
3
)
A
=
(U
3
)
B
= 0, make it clear that the flow field remains “two-dimensional” and
also has only two components. Thus for the inflow and outflow the following
equation can be derived from the continuity equation, where b is the width
of the blade in the x
3
direction:
ρ(U
1
)
A
tb = ρ(U
1
)
B
tb. (8.92)
For the inflow and outflow the same velocity components in the x
1
direction
thus result. This makes it clear that the purpose of the blades is to change
the velocity component (U
2
)
A
of the approaching flow.
For the computation of the force on a row of blades, a control volume
(a, b, c, d). is chosen, as shown in Fig. 8.9. In the flow direction, two flow
lines are chosen as boundaries of the control volume which are positioned
along (a − b)and(d − c), with the distance of the blades being t. Hence
the inflow and outflow to the chosen control volume take place only over the
areas (d − a)b and (c − d)b.
When one neglects gravitational effects, the Bernoulli equation yields the
following relationship between the velocity and pressure fields:
P
A
ρ
+
1
2
(U
1
)
2
A
+(U
2
)
2
A
entire kinetic energy in (A)
=
P
B
ρ
+
1
2
(U
1
)
2
B
+(U
2
)
2
B
.
entire kinetic energy in (B)
(8.93)
For the computation of the force on the blade, the integral form of the
momentum equation is used:
∂
∂t
⎛
⎝
#
V
K
ρU
j
dV
⎞
⎠
+
#
O
K
ρU
i
U
j
dA
i
= −
#
O
K
P dA
j
−
#
O
K
τ
ij
dA
i
+
#
V
K
ρg
j
dV +
F
j
.
(8.94)
With the following assumptions, one obtains from (8.94)
∂
∂t
#
V
K
ρU
j
dV
p
=0, as there is a stationary flow
#
O
K
τ
ij
dA
i
=0, as the flow is that of a viscosity-free fluid
#
V
K
ρg
j
dV =0, as gravitational forces are negligible,
(8.95)
242 8 Integral Forms of the Basic Equations
and the momentum equation in simplified form:
#
O
K
ρU
i
U
j
dA
i
= −
#
O
K
P dA
j
+
F
j
oder F
j
=
#
O
K
ρU
i
U
j
dA
i
+
#
O
K
P dA
j
.
(8.96)
Hencefortheforcesinthedirectionsj =1andj =2:
F
1
=˙m [(U
1
)
B
− (U
1
)
A
]
=0
+(P
B
− P
A
) bt =(P
B
− P
A
) bt. (8.97)
F
2
=˙m [(U
2
)
B
− (U
2
)
A
]. (8.98)
From the Bernoulli (8.93), one obtains
(P
B
− P
A
)=
ρ
2
7
(U
2
)
2
A
− (U
2
)
2
B
8
. (8.99)
Hence for F
1
the following results:
F
1
=
ρ
2
Bt
7
(U
2
)
2
A
− (U
2
)
2
B
8
, (8.100)
or, expressed in terms of the in-flow angle and the out-flow angle:
F
1
=
ρ
2
Bt
7
U
2
A
sin
2
α
A
− U
2
B
sin
2
α
B
8
, (8.101)
and
F
2
= −ρ · Bt [U
A
sin α
A
− U
B
sin α
B
], (8.102)
where F
1
and F
2
are the forces acting on the control volume. The forces
acting on the blades are
(F
1
)
s
= −F
1
= −
ρ
2
bt
7
U
2
A
sin
2
α
A
− U
2
B
sin
2
α
B
8
. (8.103)
(F
2
)
s
= −F
2
= ρbt [U
A
sin α
A
− U
B
sin α
B
]. (8.104)
The blade thus experiences a force (F
1
)
s
in the negative x
1
direction and a
force (F
2
)
s
in the positive x
2
direction. It is the force in the x
2
direction that
drives the set of blades in Fig. 8.9.
8.5.9 Euler’s Turbine Equation
The considerations in Sect. 8.5.8 related to a set of blades arranged in a plane,
which is located in a x
1
−x
2
plane. Arranging the blades radially, a rotating
wheel results as shown in Fig. 8.10, one obtains the basic arrangement of
a radial turbine. The term “radial” designates the main flow direction in
which the flow through the turbine blades takes place, namely radially from

8.5 Applications of the Integral Form of the Basic Equations 243
Fig. 8.10 Diagram showing schemati-
cally the flow through a radial turbine
the inside of the impeller to the outside. When employing the continuity
equation, one obtains
ρ(U
r
)
A
(2πr
A
)b = ρ(U
r
)
B
(2πr
B
)b, (8.105)
or, stated differently, the demand for mass conservation results in the
following relationship:
(U
r
)
B
=
r
A
r
B
(U
r
)
A
. (8.106)
From the Bernoulli equation, the following results:
P
A
ρ
+
1
2
7
(U
r
)
2
A
+(U
t
)
2
A
8
=
P
B
ρ
+
1
2
7
(U
r
)
2
B
+(U
t
)
2
B
8
. (8.107)
From the integral form of the momentum equation, one can determine for
the force in the radial direction, if b
A
= b
B
= b is introduced:
F
r
=˙m [(U
r
)
B
− (U
r
)
A
]+2π(r
B
P
B
− r
A
P
A
)b. (8.108)
Furthermore, for the force in the tangential direction the following holds:
F
t
=˙m [(U
t
)
B
− (U
t
)
A
] . (8.109)
For the moment imposed on the control volume by the running wheel, one
can derive:
M
t
=˙m [r
B
(U
t
)
B
− r
A
(U
t
)
A
] . (8.110)
The mechanical power output, resulting from the turbine, amounts to:
P
turb
= −M
t
ω = − ˙mω [r
B
(U
t
)
B
− r
A
(U
t
)
A
] . (8.111)
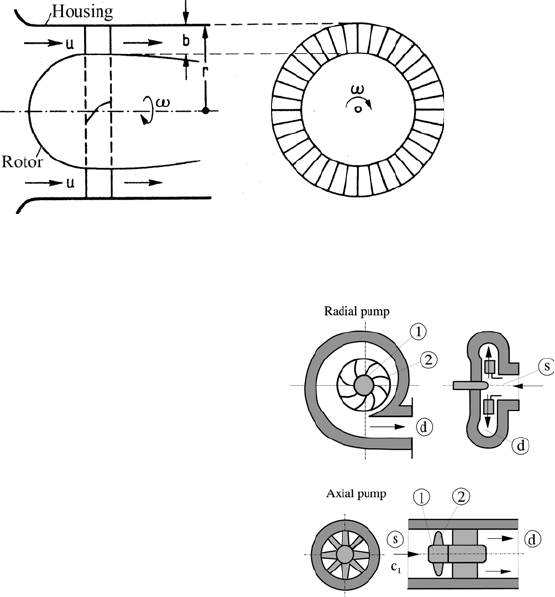
244 8 Integral Forms of the Basic Equations
Equations (8.110) and (8.111) are referred to in the literature as Euler’s
turbine equation. Here, for r
A
= r
i
, the “inflow radius” of the blade rim is
assumed, and for r
B
= r
0
=, the “outflow radius” is set.
The resulting equation holds not only for turbines, but also generally for
flow machines, such as compressors, air blowers (ventilators), pumps, etc.
Here pumps and turbines differ in the considerations carried out only with
regard to the sign of the energy exchange between running wheel and flowing
fluid. In a turbine, energy is extracted from the fluid flow, so that one can
collect a usable moment at the shaft of this power engine, or the corresponding
energy can be extracted. In a pump, on the other hand, energy is supplied to
the fluid flow via the “running wheel”, i.e. a torque for driving the machine
is exerted at the shaft. Thus the energy necessary for pumping is supplied in
pumps to the fluid.
Finally, it is mentioned that Euler’s turbine equation can also be applied
to flow machines through which flows pass axially, as Figs. 8.11 and 8.12 show
them.
Fig. 8.11 Diagram of the course of the flow through an axial turbine
Fig. 8.12 Schematic representation of radial
and axial pumps
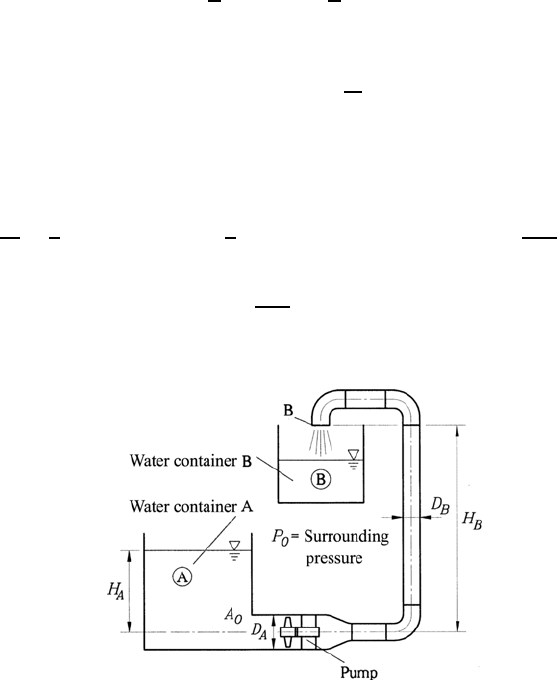
8.5 Applications of the Integral Form of the Basic Equations 245
8.5.10 Power of Flow Machines
In Fig. 8.13, a typical application of a flow machine is shown schematically.
In the chosen case, the application of a pump is shown as an example. It
sucks on the intake side a certain quantity of water ˙m in order to transport
it upwards at its discharge side. Here, differences exist in the pipe diameter
between the intake side and the discharge side of the pump.
The suction of the pumped fluid takes place from a container (A) and
the transport is carried out into a container (B), as shown schematically in
Fig. 8.13. All quantities located at the suction side of the considered problem
are designated by the subscript A, the quantities on the discharge side of the
pump by B.
From the integral form of the continuity equation, the following results for
the considered pumping fluid problem:
ρ
A
π
4
D
2
A
˜
U
A
= ρ
B
π
4
D
2
B
˜
U
B
. (8.112)
For ρ
A
= ρ
B
= ρ = constant, the following results:
D
2
A
˜
U
A
= D
2
B
˜
U
B
=
˙m
ρ
=
˙
V. (8.113)
For the computation of the required pumping power, it is recommended
to employ the integral form of the mechanical energy equation, as stated in
(8.24):
∂
∂t
#
V
K
1
2
ρU
2
j
dV +
#
O
K
ρU
i
1
2
U
2
j
dA
i
= −
#
O
K
PU
j
dA
j
+
#
V
K
P
∂U
j
∂x
j
dV
−
#
O
K
τ
ij
U
j
dA
i
+
#
V
K
τ
ij
∂U
j
∂x
i
dV +
#
V
K
ρg
j
˙
V dx
j
+
˙
E. (8.114)
Fig. 8.13 Diagram for the computation of the pumping capacity
246 8 Integral Forms of the Basic Equations
Reducing this equation by simplifying assumptions that apply to the present
flow problem:
∂
∂t
#
V
K
1
2
ρU
2
j
dV = 0 stationary pumping conditions (8.115)
#
V
K
P
∂U
j
∂x
j
dV = 0 no work done during expansion, as ρ = constant and thus
∂U
j
∂x
j
=0, (8.116)
and neglecting the τ
ij
terms in the above integral energy equation, one
obtains:
#
O
K
ρU
i
1
2
U
2
j
dA
i
= −
#
O
K
PU
j
dA
j
+
#
V
K
ρg
j
U
j
d
˙
V +
˙
E, (8.117)
or
− ˙m
1
2
˜
U
2
A
+
1
2
˜
U
2
B
=
˙
V
A
P
A
−
˙
V
B
P
B
+ ρg
˙
VH
C
+ p
m
, (8.118)
where P
m
represents the power transferred by the pump into the fluid. For
the required mechanical power of the pump, the following holds:
P
m
=
˙
V
<
ρ
2
˜
U
2
B
+ P
B
+ ρgH
C
−
ρ
2
˜
U
2
A
+ P
A
=
. (8.119)
When one now considers P
B
and P
A
in more detail, the following can be said:
P
B
= P
0
and hence P
A
= P
0
+ ρgH
A
−
ρ
2
U
2
A
and
˜
U
A
≈ 0,
and
U
A
=
˙
V
F
A
and hence U
B
=
˙
V
F
B
Therefore, one obtains the following relationship:
P
m
=
˙
V
⎧
⎨
⎩
ρ
2
*
˙
V
2
F
2
B
−
˙
V
2
F
2
A
+
− ρgH
A
+
ρ
2
*
˙
V
F
A
+
2
+ ρgH
C
⎫
⎬
⎭
(8.120)
or, summarized:
P
m
=
ρ
2
*
˙
V
3
F
2
B
+
+ ρg (H
C
− H
A
)
˙
V. (8.121)
For the electrical power p
e
of the pump, the following results, with η being
the efficiency factor:
