Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

206 7 Similarity Theory

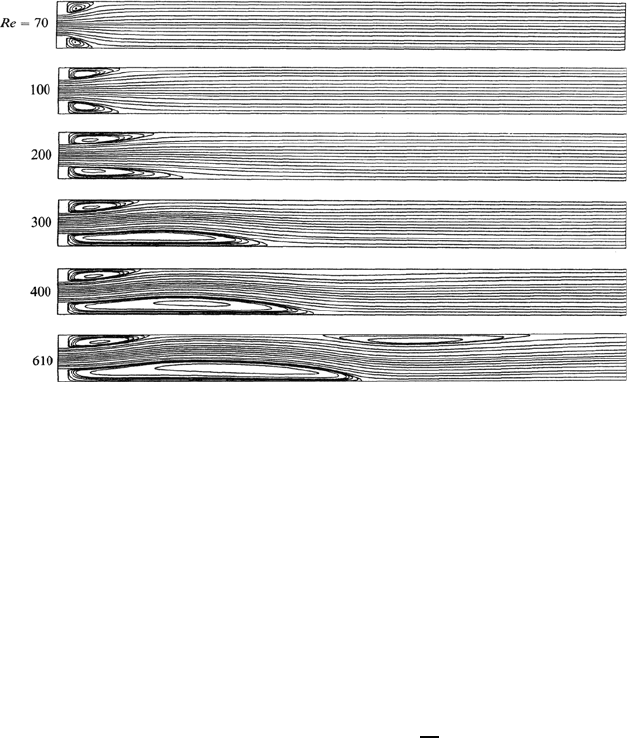
Fig. 7.6 Streamlines for the ﬂow ﬁeld of sudden channel expansion as a function of

the Reynolds number

in test sections that are similar in the strictly geometric sense. This holds,

of course, not only for the results from experimental investigations but also

for results from numerical ﬂow computations. The streamlines of the ﬂow

ﬁelds computed for diﬀerent Reynolds numbers and represented in Fig. 7.6

for a sudden channel expansion are identical for all Newtonian ﬂuids and for

large and small dimensions as long as always only the corresponding Reynolds

number is present.

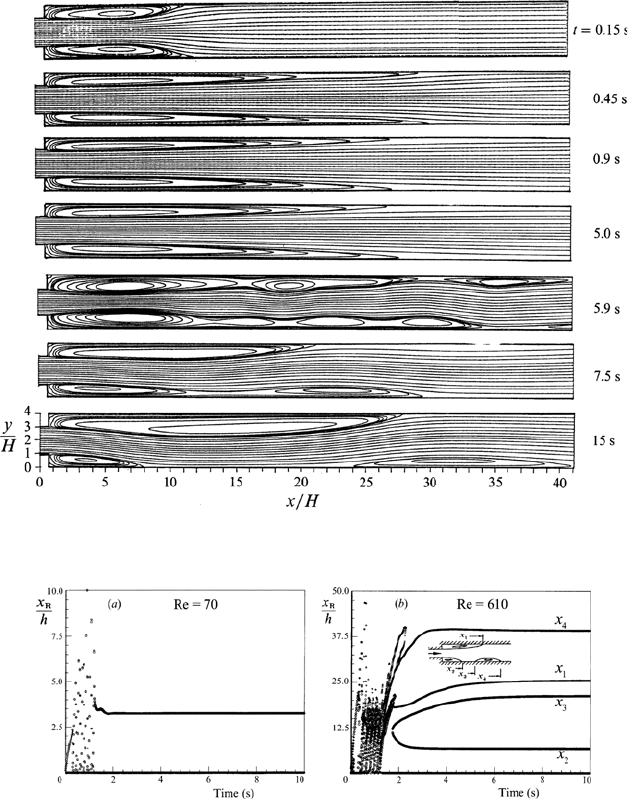
If the ﬂow represented in Fig. 7.6 by its streamlines for Re = 610 is started

from rest, a temporal path of the streamlines results as depicted in Fig. 7.7.

Here the time until the ﬂow reaches its stationary ﬁnal state is a multiple of

the characteristic time of the ﬂow, i.e. t

stat

∼ t

∼

. Thus, when one wants

to reach the stationary state of the ﬂow quickly, i.e to reach a certain ﬁnal

Reynolds number, one has to choose small dimensions and high velocities,

both being chosen to yield Re = 610.

To what extent a numerically computed ﬂow is stable depends on the in-

ﬂuence of disturbances which one can impose on the ﬂow without changing

its stationary ﬁnal state. The stability of the ﬂows for the sudden channel

expansion for Re = 70 and 610 is shown in Fig. 7.8. Disturbances im-

posed at the inlet of the test section yield temporal changes of the rate

of inﬂow and these lead to strong temporal changes of the spatial di-

mensions of the separation regions behind the step of the sudden channel

expansion.

7.2 Dimensionless Form of the Diﬀerential Equations 207

Fig. 7.7 Temporal changes of the streamlines of a transient ﬂow in a sudden channel

expansion for Re = 610

Fig. 7.8 Time variation of the length of separation regions in channel ﬂow with

sudden expansion because of imposed disturbances. The ﬂow is stable with respect to

the imposed disturbances as it reverts to its original condition after the disturbance

has faded away

7.2.4 Importance of Viscous Velocity,

Time and Length Scales

In ﬂuid mechanics, there is a multitude of problems, outside the scope of civil

engineering, where gravitational forces are unimportant. This is equivalent

208 7 Similarity Theory

to the statement that large Froude numbers exist and that therefore the

normalized momentum equation (7.13) can be written as follows:

∗

⎡

⎢

⎣



 

· U

∂U

∗

∂t

∗

+ U

∗

∂U

∗

∂x

∗

⎤

⎥

⎦

= −





∆P

∂P

∗

∂x

∗

−

1/Re





∂τ

∗

∂x∗

. (7.32)

Completing this equation with the dimensionless molecular-dependent mo-

mentum transport from (7.16):





∗

= −µ

∗

∂U

∗

∂x

∗

∂U

∗

∂x

∗

∂U

∗

∂x

∗

(7.33)

one obtains a dependence of the solutions of ﬂow problems on the following

dimensionless characteristic numbers:

St =

· U

= Strouhal number Eu =

∆P

= Euler number

Re =

= Reynolds number C =

=Shearnumber.

(7.34)

Considering these dimensionless characteristic numbers, it becomes under-

standable that the basic equations of ﬂuid mechanics deliver uniform solutions

also in the case that one chooses the characteristic quantities of ﬂow problems

such that all characteristic numbers produce the value 1, i.e.

Re =

=1 ; U

(7.35)

Eu =

∆P

=1 ; ∆P

= τ

. (7.36)

With the quantities

St =

=1 and C =

= 1 (7.37)

one obtains the following characteristic time and length scales:

= t

. (7.38)

These characteristic quantities suggest that ﬂuid ﬂows in diﬀerent ﬂow ge-

ometries can be grouped in a uniform representation. Thus the characteristic

ﬂow properties can be described by the following set of diﬀerential equations

that are free from dimensionless characteristic numbers:

7.2 Dimensionless Form of the Diﬀerential Equations 209

continuity equation:

∂ρ

∗

∂t

∗

∂(ρ

∗

)

∂x

∗

= 0 (7.39)

momentum equations (j =1, 2, 3): ρ

∗



∂U

∗

∂t

∗

+ U

∗

∂U

∗

∂x

∗



= −

∂P

∗

∂x

∗

−

∂τ

∗

∂x

∗

(7.40)

molecular momentum transport: τ

∗

= −µ

∗

∂U

∗

∂x

∗

∂U

∗

∂x

∗

∂U

∗

∂x

∗

(7.41)

The dependence of ﬂow results on the dimensionless characteristic numbers

occurs in the solutions of (7.39)–(7.41) via the imposed boundary conditions.

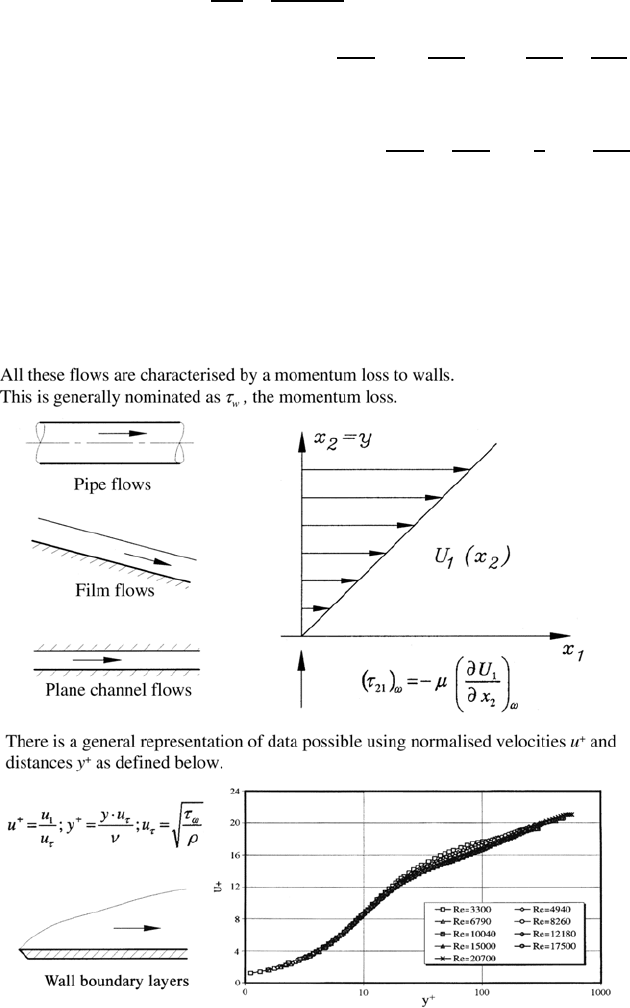
Thus for all ﬂows in Fig. 7.9, a uniform representation of measuring results

near the wall is achieved.

Fig. 7.9 Standardized ﬂow proﬁles near the wall as a function of the standardized

distance from the wall for channel, tube, ﬁlm and ﬂat plate boundary layer ﬂows

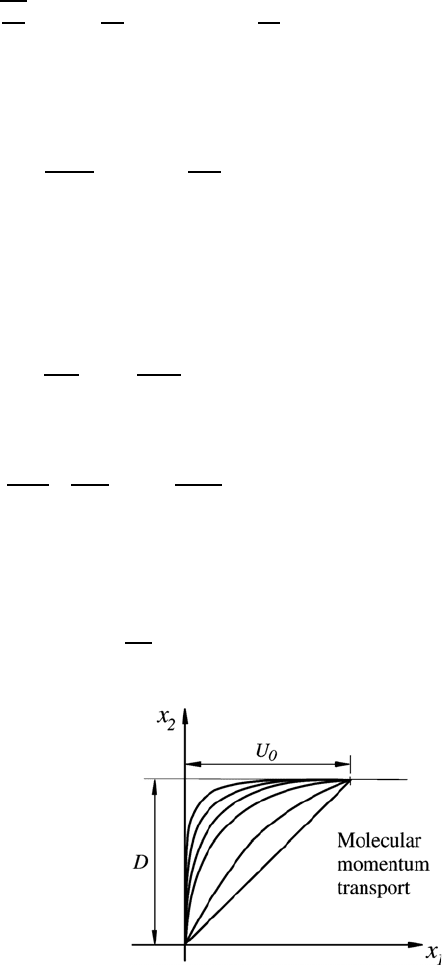
210 7 Similarity Theory

The above representations have shown that for ﬂuid ﬂow measurements

for Newtonian media, the occurrence of velocity gradients are controlled by

the presence of characteristic viscous velocity, time and length scales. These

can be stated for τ

= τ

, ρ

= ρ and µ

= µ as follows:

; t

;andL

. (7.42)

When employing these characteristic quantities, the general representation

of velocity proﬁles in turbulent wall boundary layer ﬂows results, indicated

in Fig. 7.9. In this ﬁgure the following quantities are plotted:

(y)

where y is the distance from the wall.

The importance of the quantities in (7.42) becomes obvious when one

tries to solve some typical ﬂow problems, e.g. the one-dimensional diﬀusion

problem which is sketched in Fig. 7.10, described by the following diﬀerential

equation:

∂U

∂t

= −µ

∂

∂x

. (7.43)

After normalization, the equation can be written as





∂U

∗

∂t

∗

=+µ

∗

∂

∗

∂x

∗2

. (7.44)

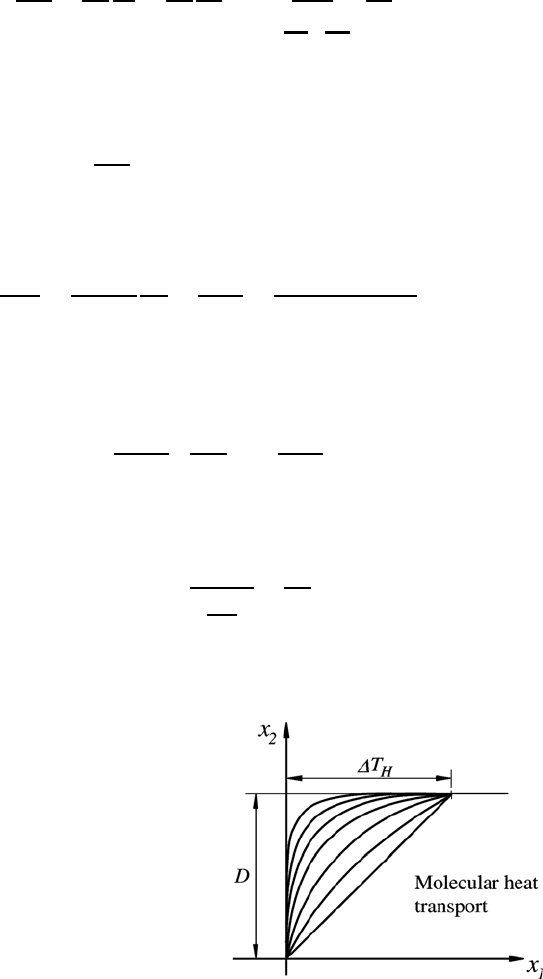
From this one can deduce for the time which is required by the molecules to

transport the momentum, entering at the position x

= 0, and transporting

it over the distance D, the following relationship:

Diﬀ

. (7.45)

Fig. 7.10 Considerations of molecular-

dependent momentum transport in ﬂuid

ﬂows

7.2 Dimensionless Form of the Diﬀerential Equations 211

Forming the relationship t

Diﬀ

=(D

/ν)/(u

/ν), one obtains the diﬀusion

time expressed as a multiple of viscous time units:

Diﬀ





  



, (7.46)

i.e. for the momentum diﬀusion problem sketched in Fig. 7.10 the following

holds:

Diﬀ

= Re

(2Eu). (7.47)

This relationship makes it clear that the dimensionless characteristic numbers

can be understood also as relationships for characteristic times, e.g.,

Re =

(D/U

)

Diﬀ

Conv

Diﬀusion time

Convection time

. (7.48)

The molecular-dependent heat transfer occurs in an analogous way to the

momentum transport, as shown in Fig. 7.11. From this results the temporal

formation of the temperature proﬁle between the planes x

=0andx

= D:



ρD



∂T

∗

∂t

∗

= λ

∗

∂

∗

∂x

∗2

(7.49)

and the diﬀusion time thus ensures that for the temperature propagation

problem, the following holds:

Diﬀ

)



ρc



, (7.50)

where a is the thermal diﬀusion constant.

Fig. 7.11 Considerations of the

molecular-dependent heat transfer in

ﬂuid ﬂows

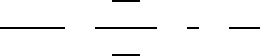
212 7 Similarity Theory

The above representations show that the momentum and heat diﬀusion

processes in ﬂuids occur in an analogous way. The ratio of the resulting

diﬀusion times is

Diﬀ

)

Diﬀ

)









µc

= Pr. (7.51)

For Prandtl numbers larger than 1, the resulting linear temperature distri-

bution between plates at x

=0andx

= H in Fig. 7.11 is formed more slowly

than the analogous linear velocity distribution in Fig. 7.10. In contrast, for

Prandtl numbers smaller than 1, the development of the linear temperature

proﬁle is quicker than that of the velocity proﬁle.

7.3 Dimensional Analysis and π-Theorem

The formal tool of the similarity theory, illustrated in many ways in the

preceding sections, is dimensional analysis, if the diﬀerential equations de-

scribing the ﬂow problem are not known. Its special importance lies in the

fact that it can also be employed when the physical relationships between

quantities are not known at all. Dimensional analysis proves to be a gener-

ally valid method to recognize the information structure in the relationships

between physical quantities in a precise and clear way. It starts from the

fact that in quantitative natural science the descriptive quantities, as illus-

trated before, have dimensions and can be divided correspondingly into basic

quantities and derived quantities. In the framework of ﬂuid mechanics, one

could regard length, time and mass as (dimensional) basic quantities and,

e.g. area, volume, velocity, acceleration, pressure (or shear stresses), energy,

density and (dynamic and kinematic) viscosity, in relation to them, as derived

quantities. This classiﬁcation has an important consequence that the units

in which the basic quantities are measured can be chosen independently, and

those of the dependent quantities are determined by this choice. Thus, with

the units metre (m), second (s) and kilogram (kg) for the basic quantities,

the derived quantities are:

Area: m

Volume: m

Velo city: m s

−1

Acceleration: m s

−2

Pressure (or shear stress): kg m

−1

−2

Energy: kg m

−2

Density: kg m

−3

Dynamic viscosity: kg m

−1

Kinematic viscosity: m

−2

−1

7.3 Dimensional Analysis and π-Theorem 213

In particular the rule then follows that amodiﬁcationof the units of

the basic quantities entails also amodiﬁcationof the units of the derived

quantities. This principle determines formally the dimensions of the de-

rived quantities from the dimensions length (L), time (t)andmass(M)of

the basic quantities. The dimensions of the above-derived quantities are:

Area: L

Volume: L

Velo city: Lt

−1

Acceleration: Lt

−2

Pressure (or shear stress): ML

−1

−2

Energy: ML

−2

Density: ML

−3

Dynamic viscosity: ML

−1

Kinematic viscosity: L

−1

Each physical quantity is characterized quantitatively by its unit and the

numerical value related to this unit. When one modiﬁes the unit by a factor

λ, the numerical value changes by the inverse factor λ

−1

The interdependent relationships between physical quantities, shown many

times in examples, relate to their numerical values. As a generally valid state-

ment, based on the dimensional analysis, the interdependent relationships

between physical quantities are dimensionally homogeneous, i.e. they are

valid independent of the choice of the units. This rule can also be expressed

in the following way: The relationships are invariant towards all changes of

units, i.e. changes of scales of the basic quantities, although the quantities

appearing individually in them possess units, i.e. scales.

The overall consequence of this statement becomes clear by a mathemat-

ical observation: the set of all modiﬁcations of scale of the basic quantities

meets the conditions, not described here in detail, of the (mathematical)

group concept. The latter is often associated with the concept of symmetry:

the elements of the group are operations on a certain object which do not

change this object. Just as the reﬂection of a circle along one of its diameters

leaves the circle unchanged (invariant) and thus is a symmetry operation of

the circle; all scale transformations of the physical basic quantities can be

understood as symmetry operations of these relationships, as they do not

change the interdependent relationships. The formal objective of the dimen-

sional analysis is to work out these circumstances and their consequences.

The consequence can be stated as follows:

The scale-invariant relationships between scale-possessing physical

quantities can be represented in the form of relationships between

scale-invariant quantities.

The direct objective of dimensional analysis is to develop the methodology for

determining from a given relation the number and form of the scale-invariant

quantities, the so-called characteristic numbers, to which this relation can

be attributed. This objective is summarized in the π-theorem.

214 7 Similarity Theory

A deeper reason for the occupation with dimensional analysis, which in its

nucleus is represented in the π-theorem, lies in the beneﬁt to be gained from

it. The practical beneﬁt of dimensional analysis for ﬂuid mechanics

lies in the possibility of scale transfer. Dimensional analysis has its

origin in the variety of (passive) considerations on the same physical situation,

arising from the choice of the scales concerning the units and the numerical

values of the basic quantities. However, owing to dimensional homogeneity

only, the numerical values of the physical quantities enter into the physical

interdependent relationships, and their scaling can be separated from the

units of these quantities. Dimensional analysis therefore can be considered

also as scaling of the numerical values of ﬁxed units, i.e. as an instrument of

(active) scale transfer.

Dimensional analysis assures, however, that the physical relationships are

always attributed to relationships that comprise dimensionless quantities (so-

called characteristic numbers). When a physical relation is described by a

diﬀerential equation, the method illustrated in Sect. 7.2 can be applied and

by normalization of the equation a set of characteristic numbers can be deter-

mined. When this form of equation of the physical relation does not exist, one

has to make use of the π-theorem in order to determine a set of characteristic

numbers describing the physical problem. This theorem makes a statement

on the relevant number of characteristic numbers: it is equal to the number of

variables minus the maximum number of variables with which no dimension-

less characteristic number can be formed. The theorem also gives a recipe for

the construction of the characteristic numbers. For both aspects the so-called

dimensional matrix is employed, which can be formed from the quantities of

the problem. Expressed by this matrix:

The number of the dimensionless characteristic numbers of a phys-

ical problem, for which a complete set of dimensional quantities is

available, is equal to the total number of the dimensional quantities

minus the rank of the dimensional matrix.

The setting up of the dimensional matrix is shown below for some typical

examples, starting from the following (mechanical) basic quantities:

M =mass(kg); L =length(m); t =time(s)

The chosen units are stated in parentheses. Each mechanical quantity can

now be traced in its dimension to the above basic quantities mass, length

and time, so the following holds:

[Q]=M

. (7.52)

When a mechanical problem depends on the quantities Q

,...,

,...,Q

n−1

, it holds that

]=M

. (7.53)

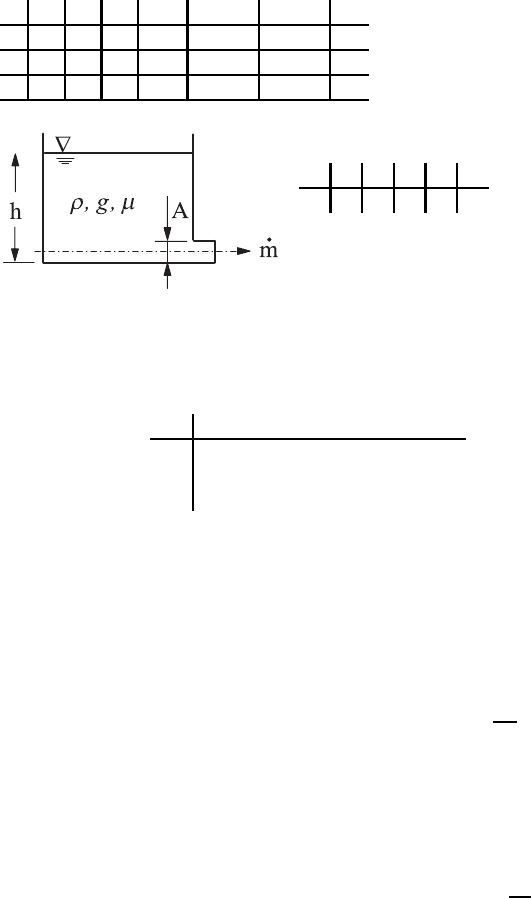
7.3 Dimensional Analysis and π-Theorem 215

Example 1: Fluid Flowing out of a Container

For this physical problem, the following dimensional matrix can be given:

n−2

n−1

M α

1(n−2)

1(n−1)

L α

2(n−2)

2(n−1)

T α

3(n−2)

3(n−1)

Matrix with rank r =3,

and n inﬂuencing param-

eters, yield the quantity

of π-numbers: π =(n − r)

˙m ρ g h A µ

n = 6 inﬂuencing parameters, i.e. ˙m = f (ρ, g, h, A, µ).

With the above determination of the quantities relevant for a ﬂuid ﬂowing

out of a container, the following dimensional matrix can be set up:

˙mA g ρ h µ

M 10 0 10 1

02 1−31−1

−10−200−1

From the below-stated considerations with rank r = 3, three dimensionless

characteristic numbers result, π

,π

and π

When one chooses as a ﬁrst determinant variable ˙m,oneobtains

[˙m][h]

[µ]

=(MT

−1

)(L

)(M

−β

)=M

, (7.54)

i.e. (1 + β)=0;(−1 − β)=0;α − β =0

or β = −1andα = β ; and thus π

˙m

hµ

. (7.55)

where π

is the Reynolds number.

Choosing as a second determinant variable A,oneobtains

[A][h]

=(L

)(h)

= M

, (7.56)

i.e. (2 + α)=0 ; α = −2 ; and thus π

, (7.57)

where π

is the geometric similarity number.