Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

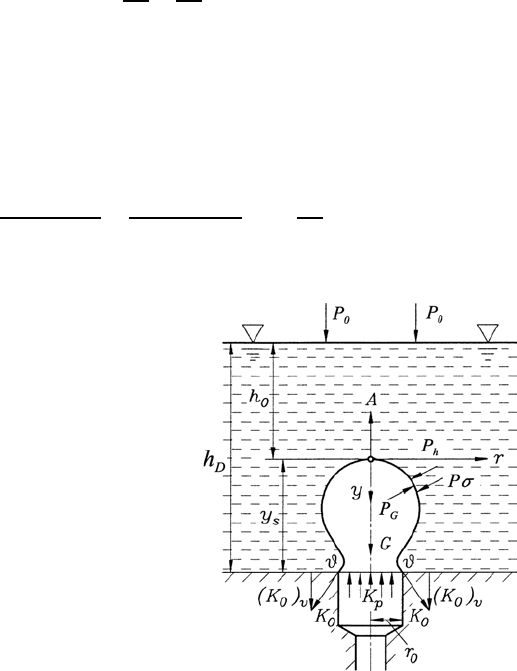
176 6 Hydrostatics and Aerostatics

forces. Although in practice this kind of bubble formation exists only to a

very limited extent, static bubble formation has a certain importance. As

it is analytically treatable, some important basic knowledge can be gained

from it which contributes to the general understanding of bubble formation,

also under dynamic conditions. Furthermore, knowledge is required on static

bubble formation in order to investigate the inﬂuences of the accelerative and

frictional forces in the case of the dynamic formation of bubbles.

The essential basic equations of static bubble formation can be derived

from the equilibrium conditions for the pressure forces at a free surface

element of the bubble.

For the pressure equilibrium at an element, the following relationship of the

interface boundary surface holds, in accordance with Fig. 6.19. This means

that the gas pressure in the bubble p

has to be equal to the sum of the

hydrostatic pressure p

and the capillary pressure p

= p

+ p





σ + p

+ ρ

g (h

+ y) (6.70)

Here the gas pressure is

= p

G,0

+ ρ

gy (6.71)

When one considers the deﬁnition for the normalized radii of curvature, em-

ploying the Laplace constant, one obtains

= R

/a,¯r = r/a,¯y = y/a.

Hence the following diﬀerential equation can be derived:

¯y



(1 + ¯y



)

3/2

¯y



¯r (1 + ¯y



)

1/2



− ¯y



(6.72)

Fig. 6.19 Equilibrium of forces at the

bubble interface (A, buoyancy force; G,

gravity; h

, distance of the nozzle from

the ﬂuid surface; h

, distance of the bub-

ble vertex from the ﬂuid surface; K

surface forces; K

, pressure forces; P

hydrostatic pressure; P

, atmospheric

pressure on the ﬂuid surface)

6.3 Free Fluid Surfaces 177

By the substitution of

¯z =

¯y





1+¯y



=sinϑ (6.73)

the diﬀerential equation of second order can be replaced by a system of two

diﬀerential equations of ﬁrst order:

d¯r

(¯r¯z)=2¯r



− ¯y



(6.74)

d¯y

d¯r

¯z

√

1 − ¯z

=tanϑ (6.75)

which are used for integration. The desired bubble volume

V is obtained in

dimensionless form by the following partial integration:

V = π

¯y

¯r

d¯y = π¯r

¯y − 2π

¯y

¯r¯y d¯r (6.76)

and, with the use of (6.74), one obtains:

V = π¯r



¯z +¯r



¯y −



(6.77)

If one introduces again dimensional quantities, equation (6.77) can be written

as follows:

= π







¯z +



−



(6.78)

V = a

πr



¯z +



y −



(6.79)

With Laplace constant a and equation (6.73), the bubble volume V can

be written as c



V =

2σ

g (ρ

− ρ

)

πr



sin ϑ +

2σ

g (ρ

− ρ

)



y −

2σ

g (ρ

− ρ

) R



(6.80)

Equation (6.80) represents an integral property of the diﬀerential equa-

tion system (6.74) and (6.75) which was obtained from considerations of the

equilibrium of forces on a bubble surface element.

For the forces acting on a bubble as a whole (Fig. 6.19), the equilibrium

condition can be written in the form:

Vgρ

− Vgρ

+ πr



2σ

− g (ρ

− ρ

) y



=2πrσ sin ϑ (6.81)

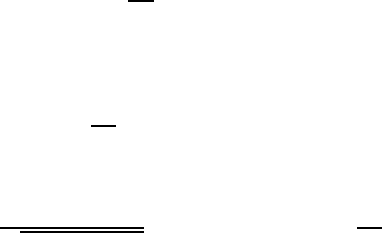
178 6 Hydrostatics and Aerostatics

where the ﬁrst two terms represent the buoyancy force and the weight of the

bubble and the third term on the left-hand side is the pressure force on the

bubble cross-section πr

at the height y. The surface forces are indicated on

the right-hand side. Equation (6.81) should be employed in cases where the

bubble volume is to be computed from the conditions of the equilibrium of

forces.

For the computation of the pressure changes during bubble formation, the

pressure in the bubble vertex can be expressed using equations (6.70) and

(6.71) and can be expressed as:

G,0

2σ

+ p

+ 

g (h

− y

) (6.82)

The pressure at the nozzle mouth varies according to (6.71) and (6.82) as

the following relationship shows:

G,D

2σ

+ p

+ 

− g (

− 

) y

(6.83)

Equation (6.83) can be written in dimensionless form:

∆¯p



2gσ (

− 

)

G,D

− p

− 

− ¯y

(6.84)

Although the diﬀerential equation system (6.74) and (6.75) permits the

computation of all bubble forms of static bubble formation and by means of

equations (6.77) and (6.84), the corresponding bubble volumes and pressure

diﬀerences can be obtained as important quantities of the bubbles, the prob-

lem with regard to the single steps of bubble formation is not determined.

The solution of the equations only allows the computation of a one-parameter

set of bubble shapes, where the vertex radius R

is introduced into the deriva-

tions as a parameter. It does not permit one to predict in which order the

diﬀerent values of the parameters are determined during bubble formation.

This has to be introduced into the considerations as additional information

in order to obtain a set of bubble forms that are generated in the course of

the bubble formation.

Theoretically, it is now possible to choose any ﬁnite set of quantities of R

0,i

values and to compute for these the corresponding bubble forms. Of practical

importance, however, is only one R

0,i

variation, which is given by most of

the experimental conditions. For these conditions, the set of R

0,i

values can

be selected as follows:

(a) All bubbles form above a nozzle with radius ¯r

(b)

0,i

= ∞ is the starting shape of static bubble formation; the horizontal

position of the interface boundary surface above the nozzle is chosen to

start computations.

0,i+1

≥

0,i

6.3 Free Fluid Surfaces 179

This means that the theoretical investigations are restricted to the bub-

ble formation which comes about through slow and continuous gas feeding

through nozzles having a radius ¯r

. Gas ﬂows through the nozzles, and thus

a decrease in the bubble volume with the selected vertex radius, as (6.77)

or (6.79) would permit, are excluded from the consideration by the imposed

relationship (c). The consequent application of this relationship leads to the

formation of a maximum bubble volume. The same has to be considered to

be the volume of the bubble at the start of the separation process, i.e. the

lift-oﬀ occurs for

(d)

max

In the computations, the diﬀerential equation system (6.74) and (6.75)

was solved numerically for diﬀerent vertex radii, considering the indicated

conditions, and thus a sequence of bubble forms was ascertained. The re-

sults of these computations are summarized in Figs. 6.20–6.25, which can be

consulted in order to understand the static bubble formation on nozzles in

liquids.

Figure 6.20 shows bubble forms that represent diﬀerent stages of bubble

formation with slow gas feeding through nozzles. The results are reproduced

for ¯r

=0.4 and this corresponds to a nozzle radius of roughly r

≈ 1.6mm

in the case of air bubble formation in water.

Figure 6.21 shows the change in the bubble volume during the formation

of gas bubbles on nozzles of diﬀerent radii ¯r

, where the vertex radius

was

chosen for designating the respective formation stage. From this diagram, it

can be inferred that a large part of the bubble forms at an almost constant

vertex radius and this is an important property for larger nozzle radii. For

−

Fig. 6.20 Bubble forms of the static bubble formation for ¯r

=0.4 computed

through integration of the equation system (6.74) and (6.75)

180 6 Hydrostatics and Aerostatics

Bubble volume

Vertex radius

Location of the maximum volume

limit of the bubble formation

Fig. 6.21 Bubble volume

V as a function of the vertex radius

for diﬀerent nozzle

radii ¯r

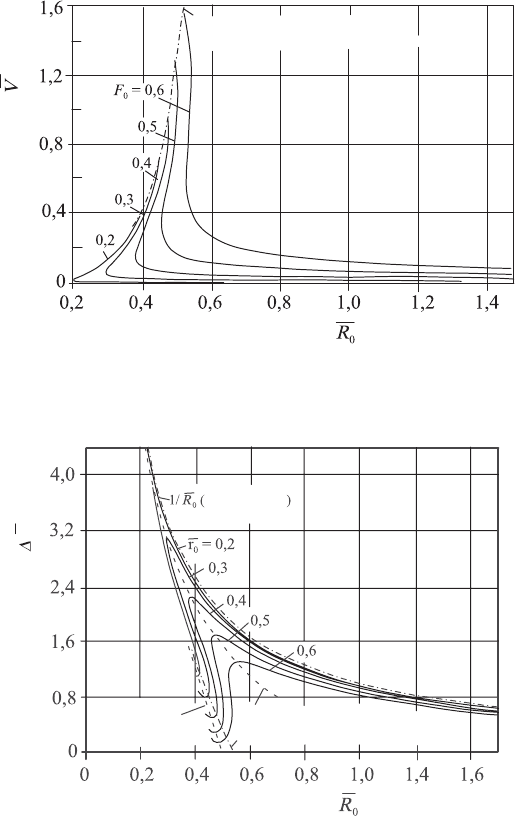
Pressure difference

Limiting line

Location of the pressure maximum

of bubble formation

Vertex radius

Position of

pressure maximum

Fig. 6.22 Pressure diﬀerence ∆

as a function of the vertex radius

for diﬀerent

nozzle radii ¯r

smaller nozzle radii, larger changes in the vertex radius are to be expected

during the formation of the gas bubbles. The vertex radius

ﬁrst decreases

and then increases again before the bubble separates from the nozzle.

In Fig. 6.22, the pressure diﬀerence ∆

as a function of the vertex ra-

dius

is represented for diﬀerent nozzle radii ¯r

. From this representation,

it can be gathered that, for static bubble formation on nozzles, initially a

continuous pressure increase at the nozzle mouth is necessary. After having

6.3 Free Fluid Surfaces 181

Location of the maximum

volume limit

Location of

maximum

vertex & location

from the nozzle

Vertex radius

Fig. 6.23 Distance of the bubble vertex ¯y

from the nozzle top as a function of the

vertex radius

for diﬀerent nozzle radii ¯r

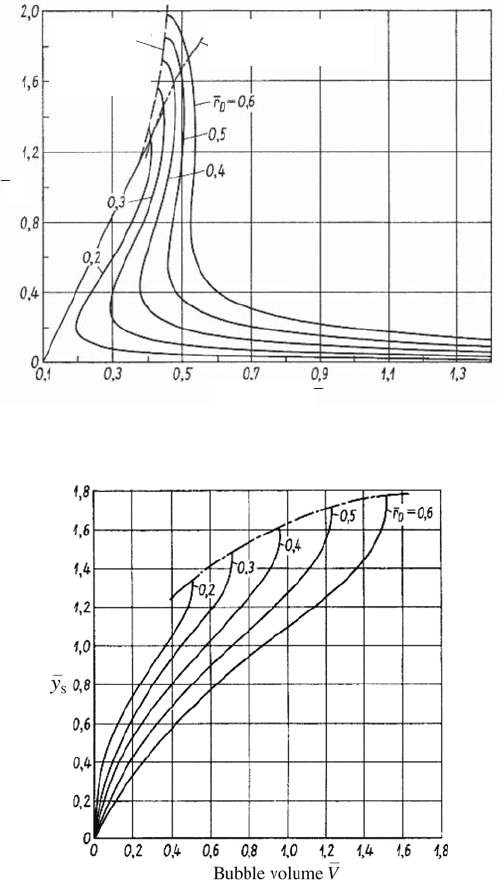
Fig. 6.24 Distance of the bubble vertex ¯y

from the nozzle top as a function of the

nozzle volume

V for diﬀerent nozzle radii ¯r

reached a maximum, distinct for all nozzle radii, the pressure decreases

again. This continuously increasing and then decreasing pressure change,

which is required for static bubble formation, makes it diﬃcult to investigate

experimentally the static formation of gas bubbles on nozzles in liquids.

182 6 Hydrostatics and Aerostatics

Bubble volume

Location of (

)

max

Pressure difference

Fig. 6.25 Pressure diﬀerence ∆

as a function of the nozzle volume for diﬀerent

nozzle radii ¯r

Figures 6.23 and 6.24 show the change in the vertex distance from the noz-

zle during bubble formation for diﬀerent nozzle radii. In Fig. 6.23, the vertex

radius was chosen for designating the respective stage of bubble formation,

whereas in Fig. 6.24 the bubble volume was employed.

Figure 6.25 represents the dimensionless pressure diﬀerence ∆

as a func-

tion of the bubble volume for diﬀerent nozzle radii ¯r

. The ﬁnal points of the

diﬀerent curves are given by the existence of a maximum bubble volume. As

can be seen from Fig. 6.22, the bubble of maximum volume above a nozzle

is not identical with that having a minimum pressure. However, the latter is

excluded from the possible bubble forms. This exclusion is due to the deﬁ-

nition of static bubble formation given above. It is stated that a continuous

gas ﬂow takes place through the nozzles towards the bubble.

For a general understanding of static bubble formation, two further facts

can be referred to:

(a) For the static bubble formation, a radius ¯r

D,gr

=0.648 exists which splits

up the static bubble formation into two diﬀerent domains. For larger ¯r

bubbles form that diﬀer in their shape from those shown in Fig. 6.20.

Theoretical investigations for nozzle radii ¯r

≥ ¯r

D,gr

were not carried

out here. They turned out to be unimportant for the introduction of

6.4 Aerostatics 183

Fig. 6.26 Bubble chains

=1.60 ascertained from the diﬀerential equation system

(6.74) and (6.75)

the results intended here for a better understanding of the principles of

bubble formation.

(b) The diﬀerential equation system (6.74) and (6.75) allows the computa-

tion of bubbles, as shown in Fig. 6.26. These bubble columns were not

investigated further, as they are not in accordance with the above-stated

air ﬂow through the nozzle for the examined static bubble formation.

Whereas static nozzle formation can theoretically be understood essen-

tially with simple mathematical means, there are considerable diﬃculties

with similar investigations of dynamic bubble formation. This is attributable

mainly to the fact that no coordinate system could be found in which dynamic

bubble formation could be described as a stationary process. Moreover, for

dynamic bubble formation, the pressure on an element of the interface bound-

ary surface is dependent on the ﬂuid motions during the bubble formation and

thus is computable only by solving the non-stationary Navier–Stokes equa-

tion. This, however, is solvable only with diﬃculty and great computing eﬀort

using numerical methods. Solutions of this ﬂuid are not treated in this book.

6.4 Aerostatics

6.4.1 Pressure in the Atmosphere

Aerostatics diﬀers from hydrostatics in the treatment of the properties of

the ﬂuid. The partial diﬀerential equations for ﬂuids at rest, derived from

the general Navier–Stokes equations, are applied along with the equation of

state for an ideal gas:

= RT (6.85)

rather than for an ideal liquid, ρ = constant.

184 6 Hydrostatics and Aerostatics

Hence the valid partial diﬀerential equations in aerostatics read:

∂P

∂x

= ρˆg

ˆg

(6.86)

or written out for j =1,2,3:

∂P

∂x

ˆg

∂P

∂x

ˆg

∂P

∂x

ˆg

(6.87)

This set of partial diﬀerential equations can now be employed for the

computation of the pressure distribution in such gases whose thermodynamic

state equation is given by (6.85). For most gases, and deﬁnitely for air under

atmospheric conditions, considerations can be carried out with the help of

this ideal gas equation. This will be made clear in the sections below with

the help of some examples.

When one considers the atmosphere of the Earth as consisting of a com-

pressible ﬂuid at rest, whose thermodynamic state can be described by the

ideal gas equation (6.85), with a precision suﬃcient for the derivations at

issue, an approximate relationship between the height above the surface of

the Earth and the pressure of the atmosphere at a considered height H can

be derived, which in general is deﬁned as the barometric height-pressure re-

lationship. In particular, the relationship known as Babinets approximation

equation will be derived here.

When one uses the coordinate system indicated in Fig. 6.27, in which the

plane x

forms a horizontal area at the level of the sea surface, the partial

diﬀerential equations (6.87) can be written as follows:

∂P

∂x

=0; P = f (x

)

∂P

∂x

=0; P = f (x

)

(6.88)

Fig. 6.27 Coordinate system for the derivation of Babinet’s approximation equation

for the atmospheric pressure above the Earth’s surface

6.4 Aerostatics 185

i.e. P = f (x

) and thus the relation

∂P

∂x

−→

holds:

= −

ˆg (6.89)

The diﬀerential equation which is to be solved can be written as follows:

= −

ˆg

= −

ˆgdx

(6.90)

with the general solution:

= −

)



ˆg



(6.91)

The integral in the above equation can be solved only when it is known

how the gravitational acceleration g changes with height and when further

the temperature variation as a function of x

can be stated. For the gravita-

tional acceleration ˆg, it is known that it changes with the height x

,exactly

speaking, with the square of the distance from the center of the Earth. This

follows directly from Newton’s law of gravitation, when the inﬂuence of the ro-

tation of the Earth is neglected. When one designates the radius of the Earth

R and when g is the gravitational acceleration at sea level, the following

relation holds:

ˆg = g





(6.92)

Taking into consideration the linear decrease in temperature with height

which often exists in the atmosphere, i.e. if one introduces:

T = T

(1 − αx

) (6.93)

one obtains the following ﬁnal relation:

= −

(1 − αx

)





(6.94)

When one now imposes restrictions concerning the height above which the

above integration is to take place and when one chooses the height such that

the following relationship holds:

αx

 1

 1 (6.95)

one can obtain by series development of the terms in brackets:

= −

(1 + αx

+ ...)



1 −

+ ...



(6.96)