Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

156 6 Hydrostatics and Aerostatics

This relationship expresses that the sum of the “pressure energy” P/ρ and

the potential energy (gx

= −g

) is constant at each point of a ﬂuid at

rest. As all points of diﬀerent ﬂuid elements possess the same “total energy”,

the driving energy gradient for motion is absent. Hence also from the energy

point of view the condition for hydrostatic ﬂuid behavior exists.

When a ﬂuid with a height h has a free surface on which an equally dis-

tributed pressure P

acts at all points, it represents, because of the relation

P = f (x

), a plane x

= h constant, i.e. a horizontal plane.

For the pressure distribution, one obtains with the boundary condition

P = P

for x

= h ; C = P

+ ρgh

P = P

+ ρg(h − x

)0≤ x

≤ h (6.13)

This relationship expresses the known hydrostatic law, according to which

the pressure in a liquid at rest increases in a linear way with the depth below

the free surface.

When one rewrites equation (6.13), one obtains:

+ gh =

+ gx

= constant (6.14)

The laws of hydrostatics are often applicable also to ﬂuids in moving

containers when one treats these in “accelerated reference systems”. The

externally imposed accelerative forces are then to be introduced as inertia

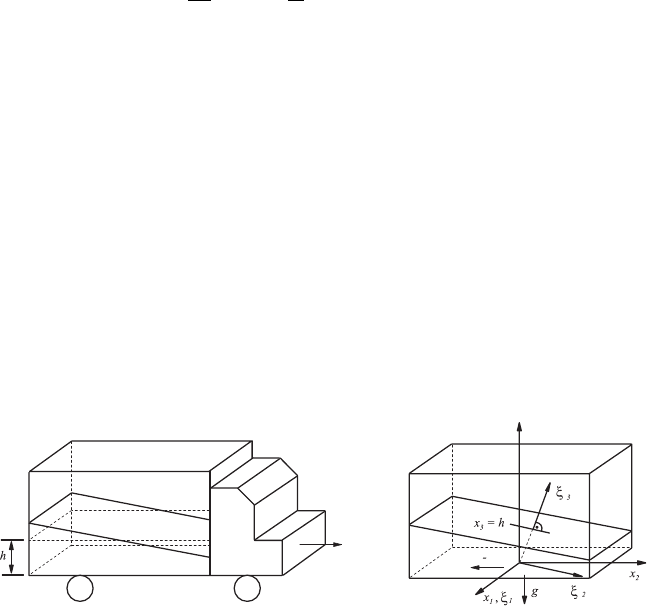
forces. Figure 6.3 shows as an example, a “container lorry” ﬁlled with a ﬂuid

whichisatrestatthetimet<t

; it then increases its speed linearly for all

times t ≥ t

, i.e. the ﬂuid experiences a constant acceleration.

In a state of rest or in non-accelerating motion, the ﬂuid surface in the

container forms a horizontal level. When the container experiences a con-

stant acceleration b, the ﬂuid surface will adopt a new equilibrium position,

provided that one disregards the initially occurring “swishing motions”.

When one now wants to compute the new position of the ﬂuid surface,

the introduction of a coordinate system x

is recommended which is closely

connected with the container. For this coordinate system, the hydrostatic

equations read as follows:

Fig. 6.3 Position of the ﬂuid level under constant acceleration

6.1 Hydrostatics 157

∂P

∂x

=0;

∂P

∂x

= −ρb;

∂P

∂x

= −ρg (6.15)

From this, the general solution results:

∂P

∂x

=0 p = f

) (6.16a)

∂P

∂x

= −ρb P = −ρbx

+ f

) (6.16b)

∂P

∂x

= −ρg P = −ρgx

+ f

) (6.16c)

By comparing the solutions, one obtains that f

, f

can only be the

sum of the terms obtained by partial integration plus a constant:

P = C − ρ(bx

+ gx

) (6.17)

Along the free surface of the ﬂuid the pressure P = P

exists and thus the

equation of the plane in which the free surface lies reads

= −

gρ

(C − P

)for−∞ <x

< +∞ (6.18)

The integration constant C is determined by the condition that the ﬂuid

volume before and after the onset of the acceleration is the same. Therefore,

the same volume holds for the moving ﬂuid and the ﬂuid at rest:

C = gρh + P

(6.19)

Hence the equation for the plane of the free surface reads

= h −

for −∞ <x

< +∞ (6.20)

As the solution of the problem has to be independent of the chosen co-

ordinate system, a coordinate system ξ

can be introduced which is rotated

against the system x

in such a way that the following equations for the

coordinate transformations hold:

= x

(axis of rotation)



+ g

(gx

+ bx

) (6.21)

and



+ g

(−bx

+ gx

)

This is equivalent to the introduction of a resulting acceleration of the quan-

tity



+ g

in the direction ξ

. Hence the basic hydrostatic equations

read

158 6 Hydrostatics and Aerostatics

∂P

∂ξ

=0;

∂P

∂ξ

=0;

∂P

∂ξ

= −



+ g

ρ (6.22)

Thus P = F (ξ

) holds and P = C − ρ



+ g

The integration constant C results from the boundary condition

P = P

+ gρh for ξ

= 0 (6.23)

P = P

+ ρg

⎛

⎝

h −





⎞

⎠

(6.24)

All further statements concerning the problem of the accelerated ﬂuid con-

tainer can also be made in the coordinate system ξ

. Along the free surface

P = P

and





= constant (6.25)

Hence this is the equation of the plane in which the free surface of the ﬂuid

in the moving container lies.

By the above treatment, it becomes clear that it is possible to employ

the basic hydrostatic laws also in accelerated reference systems, provided the

inertia forces that are attributable to the external motions are taken into

consideration. The accelerations that occur (inertial and gravitational) are

to be added in a vectorial manner to yield a total acceleration. Through this

one obtains the direction and magnitude of the total acceleration. The free

surface occurs perpendicular to the vector of the total acceleration.

The example given in Fig. 6.4 can also be categorized into the group of

examples that can be treated by means of the basic laws of hydrostatics. This

ﬁgure shows a water container which is sliding down an inclined plane with

an angle of inclination α with respect to the horizontal plane. The container

at rest possesses a water surface which is horizontal, as only the gravitational

Fig. 6.4 Water container sliding down an inclined plane. Motion with and without

friction

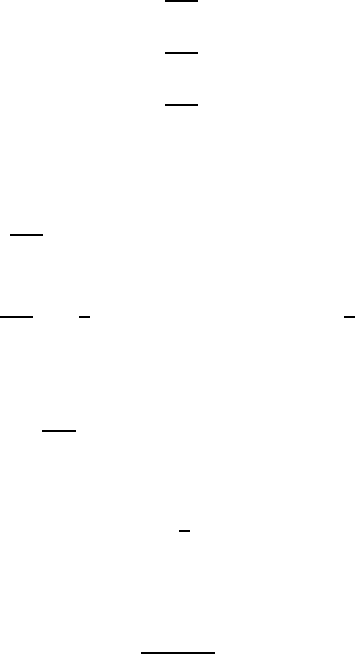
6.1 Hydrostatics 159

acceleration appears as inertia force per kg of ﬂuid. When the ﬂuid container

is released and when the acceleration directed downwards is |b| = g sin α,the

body starts to move and thus experiences an acceleration which is parallel

to the inclined plane. The resulting acceleration component acting on the

ﬂuid is composed of the component directed upwards with |b| = g sin α and

the component directed downwards with µ

g cos α.Hereµ

is the friction

coeﬃcient which characterizes the interaction between the container bottom

and the surface of the inclined plane.

When one treats ﬁrst the accelerated motion occurring downwards on

the inclined plane without friction, one obtains in the coordinate system,

indicated in Fig. 6.4, the following set of basic hydrostatic equations:

∂P

∂x

= 0 (6.26a)

∂P

∂x

= −ρg sin α cos α (6.26b)

∂P

∂x

= −ρg(1 − sin

α) (6.26c)

The pressure distribution in the container sliding downwards in Fig. 6.4 and

thus also the solution for the position of the ﬂuid surface can be obtained by

the solution of (6.26).

From

∂P

∂x

= 0, it follows on the one hand that P = f(x

) and thus

the following solution holds:

∂P

∂x

= −

ρg sin(2α) −→ P = f

) −

ρg sin(2α)x

(6.27a)

and also the solution

∂P

∂x

= −ρg cos

α −→ P = f

) − ρg(cos

α)x

(6.27b)

By comparing the solutions, one obtains:

P = C −

ρg(sin(2α)x

+2(cos

α)x

) (6.28)

Along the free surface, P = P

holds and thus one obtains as the relationship

for the location of the free surface:

= −(tan α)x

ρg cos

(C − P

)for−∞ <x

< +∞ (6.29)

As the origin of the coordinates also lies on the free surface, C = P

follows

and thus for the plane in which the free surface lies one obtains

= −(tan α)x

for −∞ <x

< +∞ (6.30)

160 6 Hydrostatics and Aerostatics

This equation shows that for a friction-free sliding along the inclined plane,

the free surface lies parallel to the plane along which the container slides.

This can also be derived from considerations of the left-hand acceleration

diagram in Fig. 6.4, in which it can be seen that the resulting acceleration b

is located vertically with respect to the inclined plane.

When one adds for the downward motion the occurring frictional force,

one obtains the following set of basic hydrostatic equations:

∂P

∂x

= 0 (6.31a)

∂P

∂x

= −ρg(sin α − µ

cos α)cosα (6.31b)

∂P

∂x

= −ρg[1 − (sin α − µ

cos α)sinα] (6.31c)

Thus the solution corresponding to (6.31) reads:

P = C − ρg[(sin α − µ

cos α)cosα]x

− ρg[1 − (sin α − µ

cos α)sinα]x

(6.32)

If one puts on the one hand P = P

, for the free surface, one obtains the

equation for the plane in which the free surface lies. When one takes further

into consideration that the origin of the coordinates lies again on the free

surface, i.e. C = P

, one obtains as the ﬁnal equation for the plane of the

free ﬂuid surface

= −



(sin α − µ

cos α)cosα

1 − (sin α − µ

cos α)sinα



(6.33)

For this general case of motion with friction along the inclined plane of the

ﬂuid container, shown in Fig. 6.4, a free liquid surface appears which is less

inclined with respect to the horizontal plane without surface friction. Atten-

tion has to be paid, however, to the fact that the derivations only hold when

≤ tan α.Forµ

≥ tan α one obtains the limiting case of a container at

rest, i.e. the frictional force is higher than the forward accelerating force.

As a last example to show the employment of hydrostatic laws in accel-

erated reference systems, the problem presented in Fig. 6.5 is considered. It

shows a rotating cylinder closed at the top and bottom, which is partly ﬁlled

with a liquid. When the cylinder is at rest, the free surface of this liquid as-

sumes a horizontal position, as the diﬀerent liquid particles only experience

the gravitational force as mass force. When the cylinder is put into rotation,

one observes a deformation of the liquid surface which progresses until ﬁnally

it becomes parabolic, as shown in Fig. 6.5.

When now on this rotating motion an additional accelerated vertical mo-

tion is superimposed, one detects that the hyperboloid can assume diﬀerent

shapes, depending on the magnitude of the vertical acceleration and on the

direction (upwards or downwards). In the following it will be shown that the

6.1 Hydrostatics 161

Fig. 6.5 Treatment of the “ﬂuid ﬂows” in a

rotating vertically moved and partly ﬁlled cylinder

issue of the shape of the hyperboloid can be answered on the basis of the ba-

sic equations of hydrostatics. For this purpose, a coordinate system is chosen

which is ﬁrmly coupled to the walls of the rotating and vertically accelerated

cylinder and which thus experiences both rotating motion and accelerated

vertical motion.

The above examples have shown that the basic hydrostatic equations are

applicable, provided that no ﬂuid motion occurs in the chosen coordinate

system and that the external acceleration forces are taken into consideration

as inertia forces. In the acceleration diagram in Fig. 6.5, it is shown that, for

the following derivations, the horizontally occurring centrifugal acceleration

r, as well as the “vertical acceleration” b, have been taken into account.

If one considers the ﬂuid ﬂow problem sketched in Fig. 6.5, in a coordinate

system (r, ϕ, z), rotating with the cylinder, one ﬁnds that all ﬂuid particles are

at rest after having reached the steady ﬁnal state of motion. With reference

to the chosen coordinate system, the prerequisites for the employment of the

basic hydrostatic equation are fulﬁlled, which in cylindrical coordinates adopt

the following form:

∂P

∂r

= ρg

;

∂P

∂ϕ

= ρg

;

∂P

∂z

= ρg

(6.34)

For g

= rω

, g

=0andg

= −(g + b) one obtains, for the problem to be

treated, the following set of basic equations and their general solution:

∂P

∂r

= ρrω

−→ P =

ρω

+ f

(ϕ, z) (6.35a)

162 6 Hydrostatics and Aerostatics

∂P

∂ϕ

=0 −→ P = f

(r, z) (6.35b)

∂P

∂z

= −ρ(g + b) −→ P = −ρ(g + b)z + f

(r, ϕ) (6.35c)

Comparison of the solutions (6.35a–c) results in:

P = C +

− ρ(g + b)z for 0 ≤ ϕ ≤ 2π (6.36)

When one introduces on the axis r = 0, for the position of the parabolic apex

z = z

, P = P

holds at the location r =0andz = z

. This yields for the

integration constant:

C = P

+ ρ(g + b)z

Therefore, the equation for the pressure distribution in the liquid body in

Fig. 6.5 reads:

P = P

− ρ(g + b)(z − z

)for0<ϕ<2π (6.37)

Along the free surface of the liquid, the following holds for the pressure P =

, so that the free surface employing (6.37) can be represented as follows:

z = z

2(g + b)

for 0 ≤ ϕ ≤ 2π (6.38)

The coordinate z

of the introduced apex position can be determined from

the condition that the liquid volume before the rotations starts, i.e. πR

has to be equal to the liquid volume which exists in rotation between the free

surface of the liquid and the cylinder walls. Thus the following holds:

πR

h =2π

rz dr =2π



2(g + b)



dr (6.39)

and carrying out the integration yields:

h =



8(g + b)





4(g + b)



(6.40)

= h −

4(g + b)

(6.41)

Inserting (6.41) in (6.38) yields:

z = h −

4(g + b)

− 2r

) (6.42)

On the basis of this, the diﬀerent forms of the free liquid surface can now be

looked at. Some typical cases are shown in Fig. 6.6. These will be discussed

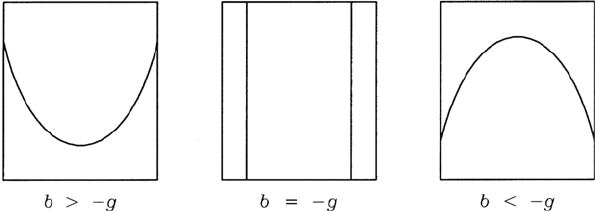
6.2 Connected Containers and Pressure-Measuring Instruments 163

Fig. 6.6 Examples of possible forms of the ﬂuid surface in a rotating vertically

accelerated cylinder

in the following on the basis of the above derivations and the derived ﬁnal

relationship. It is hoped that it will be clear to the reader how physical

information can be obtained by analytical derivations employing the basic

equations of ﬂuid mechanics, e.g. in the present example the form of the free

surface of the liquids in the containers can be calculated.

The positions of the liquid surface indicated in Fig. 6.6 can be stated by

the indicated relationship of the relative magnitudes of b and g:

b>−g: When the vertical acceleration of the container takes place up-

wards and the resultant acceleration b points downwards, with

0 >b>−g, the “opening” of the parabola is positive according

to (6.42). The liquid touches the bottom and side areas of the

container.

b = −g: When the vertical acceleration of the container takes place up-

wards with b = −g, the entire ﬂuid rests at the side wall of the

container.

b<−g: When the vertical acceleration of the container takes place down-

wards with b<−g, the “opening” of the parabola is negative

according to (6.42). The ﬂuid touches the ceiling and side areas

of the container.

All this can be deduced from (6.42) and all intermediate forms, not shown

in Fig. 6.6 can also be completed.

6.2 Connected Containers and

Pressure-Measuring Instruments

6.2.1 Communicating Containers

In many ﬁelds of engineering one has to deal with ﬂuid systems that are

connected to one another by pipelines. Special systems are those in which

164 6 Hydrostatics and Aerostatics

∇

Container 1

Container

Valve

Fig. 6.7 Sketch for explanation of the pressure conditions with communicating

containers

Fig. 6.8 Communicating containers with inclined communication tube

the ﬂuid is at rest, i.e. in which the ﬂuid does not ﬂow. Figure 6.7 represents

schematically such a system, which consists of two containers with “ﬂuids at

rest” that are connected with one another by a pipeline with a valve.

When the valve is opened, both systems can interact with one another in

such a way that a ﬂow takes place from the container with higher pressure,

at the entrance of the pipe connecting the containers, with lower pressure.

When the ﬂow through the pipe has stopped, the same ﬂuid pressure exists

on both sides of the valve, i.e.

+ ρ

g (H

− h

)=p

+ ρ

g (H

− h

) (6.43)

When there is the same ﬂuid in both containers with ρ

= ρ

= ρ the

following relationship holds:

− p

= ρg [(H

− H

) − (h

− h

)] (6.44)

For the containers shown in Fig. 6.8, the pressure P

acts on both of the top

surfaces.

Hence, introducing that the pressure over both of the free surfaces is equal,

one obtains

= p

(6.45)

and thus

− h

)=(H

− h

) (6.46)

i.e. in open communicating containers ﬁlled with the same ﬂuid, the ﬂuid

levels take the same height with respect to a horizontal plane.

6.2 Connected Containers and Pressure-Measuring Instruments 165

This is the basic principle according to which simple liquid level indicators

which are installed outside liquid containers operate. They consist of a vertical

tube connected with a container in which the liquid ﬁlled in the container

can rise. The ﬂuid level indicated in the connecting tube shows the ﬂuid level

in the container.

As a last example, open containers are considered that are connected to

one another by means of an inclined tube that is directed upwards. For these

containers, one ﬁnds that the ﬂuid surfaces in both containers adopt the

same level. When this ﬁnal state is reached (equilibrium state), no equalizing

ﬂow takes place between the containers, although the deeper lying end of

the pipe shows a higher hydrostatic pressure at the connecting point. The

reasons for the fact that an equalizing ﬂow does not occur, in spite of a

higher hydrostatic pressure at the deeper lying end of the pipe were stated

in Sect. 6.1. The energy considerations carried out there show that the total

energies of the ﬂuid particles are the same at both ends of the pipe and thus

the basic prerequisite for the start of ﬂuid ﬂows is missing.

The behavior of communicating containers that are ﬁlled with ﬂuids at rest

can often be understood easily by making it clear to oneself that the pressure

inﬂuence of a ﬂuid on walls is identical at each point with the pressure inﬂu-

ence on ﬂuid elements which one installs instead of walls. For example, the

pressure distributions in the ﬂuid container shown in Fig. 6.9 are identical

with those of the same container when components are installed to obtain

two partial containers connected with one another, in the case that the ﬂuid

surfaces are kept at the same level.

Owing to the installed walls, the pressure conditions do not change in

the right container as compared with the left container. The container areas

installed on the left replace the pressure inﬂuence of the ﬂuid particles acting

on the walls.

Fig. 6.9 Sketch for the consideration of the pressure inﬂuence on liquids at rest