Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows
Подождите немного. Документ загружается.

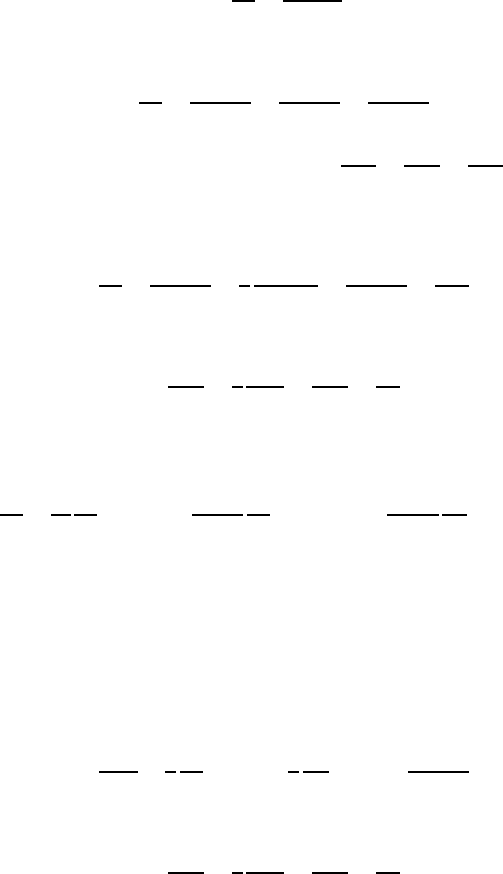
5.7 Basic Equations in Different Coordinate Systems 135
5.7 Basic Equations in Different Coordinate Systems
5.7.1 Continuity Equation
The derivations carried out for the continuity equation in Cartesian coordi-
nates resulted in
∂ρ
∂t
+
∂(ρU
i
)
∂x
i
= 0 (5.92)
or, without the application of the summation convention,
∂ρ
∂t
+
∂(ρU
1
)
∂x
1
+
∂(ρU
2
)
∂x
2
+
∂(ρU
3
)
∂x
3
=0. (5.93)
For ρ = constant on obtains:
∂U
1
∂x
1
+
∂U
2
∂x
2
+
∂U
3
∂x
3
=0
In cylindrical coordinates (r, ϕ, z)with(U
r
,U
ϕ
,U
z
), the following equation
can be derived:
∂ρ
∂t
+
∂(ρU
r
)
∂r
+
1
r
∂(ρU
ϕ
)
∂ϕ
+
∂(ρU
z
)
∂z
+
ρU
r
r
=0, (5.94)
and for ρ = constant the equation reduces to:
∂U
r
∂r
+
1
r
∂U
ϕ
∂ϕ
+
∂U
z
∂z
+
U
r
r
=0. (5.95)
In spherical coordinates (r, θ, φ), the continuity equation can be stated as
shown below for (U
r
,U
θ
,U
φ
):
∂ρ
∂t
+
1
r
2
∂
∂r
(ρr
2
U
r
)+
1
r sin θ
∂
∂θ
(ρU
θ
sin θ)+
1
r sin θ
∂
∂φ
(ρU
φ
)=0. (5.96)
The coordinates mentioned below were employed in the derivations of the
above relationships (Figs. 5.11 and 5.12).
The use of cylindrical coordinates in the derivations of the basic equations
leads to the metric coefficients introduced in Sect. 2.10 for the transformation
of the equations:
h
r
=1; h
ϕ
= r; h
z
=1
for the general continuity equation one can also write:
∂(ρ)
∂t
+
1
r
∂
∂r
(rρU
r
)+
1
r
∂
∂ϕ
(ρU
ϕ
)+
∂(ρU
z
)
∂z
=0, (5.97)
or for the continuity equation with ρ = constant:
∂U
r
∂r
+
1
r
∂U
ϕ
∂ϕ
+
∂U
z
∂z
+
U
r
r
=0. (5.98)

136 5 Basic Equations of Fluid Mechanics
Fig. 5.11 Coordinate systems and trans-
formation equations for cylindrical coordi-
nates
Fig. 5.12 Coordinate systems and
transformation equations for spheri-
cal coordinates
Analogously to the above derivations of the continuity equation in cylin-
drical coordinates, one obtains for spherical coordinates the following metric
coefficients for the transformations:
h
r
=1; h
υ
= r; h
ϕ
= r sin θ, (5.99)
and thus for the continuity equation in spherical coordinates reads:
∂(ρ)
∂t
1
r
2
∂
∂r
(ρr
2
U
r
)+
1
r sin θ
∂
∂θ
(ρU
θ
sin θ)+
1
r sin θ
∂
∂φ
(ρU
φ
)=0. (5.100)
The continuity equation in spherical coordinates with ρ = constant results
in:
1
r
2
∂
∂r
(r
2
U
r
)+
1
r sin θ
∂
∂θ
(U
θ
sin θ)+
1
r sin θ
∂
∂φ
(U
φ
)=0. (5.101)
5.7.2 Navier–Stokes Equations
Analogously to the transformation of the continuity equation into cylindrical
and spherical coordinates, the different terms of the Navier–Stokes equations
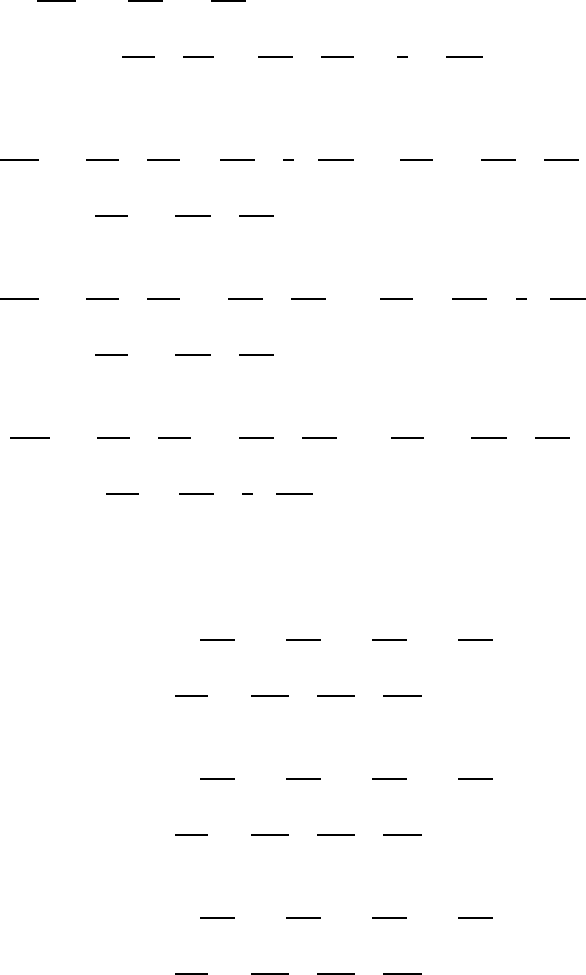
5.7 Basic Equations in Different Coordinate Systems 137
can also be transformed. These equations can be stated, for Newtonian fluids,
and in Cartesian coordinates as follows:
ρ
DU
j
Dt
= ρ
∂U
j
∂t
+ U
i
∂U
j
∂x
i
= −
∂P
∂x
j
+
∂
∂x
i
µ
∂U
j
∂x
i
+
∂U
i
∂x
j
−
2
3
µδ
ij
∂U
k
∂x
k
+ ρg
j
. (5.102)
Written out for j =1,2,3:
ρ
DU
1
Dt
= −
∂P
∂x
1
+
∂
∂x
1
2µ
∂U
1
∂x
1
−
2
3
µ(
∂U
k
∂x
k
)
+
∂
∂x
2
µ
∂U
1
∂x
2
+
∂U
2
∂x
1
+
∂
∂x
3
µ
∂U
3
∂x
3
+
∂U
1
∂x
1
+ ρg
1
, (5.103)
ρ
DU
2
Dt
= −
∂P
∂x
2
+
∂
∂x
1
µ
∂U
2
∂x
1
+
∂U
1
∂x
2
+
∂
∂x
2
2µ
∂U
2
∂x
2
−
2
3
µ(
∂U
k
∂x
k
)
+
∂
∂x
3
µ
∂U
3
∂x
3
+
∂U
2
∂x
1
+ ρg
2
, (5.104)
ρ
DU
3
Dt
= −
∂P
∂x
3
+
∂
∂x
1
µ
∂U
3
∂x
1
+
∂U
1
∂x
3
+
∂
∂x
2
µ
∂U
3
∂x
2
+
∂U
2
∂x
3
+
∂
∂x
3
2µ
∂U
3
∂x
3
−
2
3
µ(
∂U
k
∂x
k
)
+ ρg
3
. (5.105)
• Momentum Equations in Cartesian Coordinates
– Momentum equations with τ
ij
terms:
x
1
Component: ρ
∂U
1
∂t
+ U
1
∂U
1
∂x
1
+ U
2
∂U
1
∂x
2
+ U
3
∂U
1
∂x
3
= −
∂P
∂x
1
−
∂τ
11
∂x
1
+
∂τ
21
∂x
2
+
∂τ
31
∂x
3
+ ρg
1
, (5.106)
x
2
Component: ρ
∂U
2
∂t
+ U
1
∂U
2
∂x
1
+ U
2
∂U
2
∂x
2
+ U
3
∂U
2
∂x
3
= −
∂P
∂x
2
−
∂τ
12
∂x
1
+
∂τ
22
∂x
2
+
∂τ
32
∂x
3
+ ρg
2
, (5.107)
x
3
Component: ρ
∂U
3
∂t
+ U
1
∂U
3
∂x
1
+ U
2
∂U
3
∂x
2
+ U
3
∂U
3
∂x
3
= −
∂P
∂x
3
−
∂τ
13
∂x
1
+
∂τ
23
∂x
2
+
∂τ
33
∂x
3
+ ρg
3
. (5.108)

138 5 Basic Equations of Fluid Mechanics
– Navier–Stokes equations for ρ and µ both being constant:
x
1
Component: ρ
∂U
1
∂t
+ U
1
∂U
1
∂x
1
+ U
2
∂U
1
∂x
2
+ U
3
∂U
1
∂x
3
= −
∂P
∂x
1
+ µ
∂
2
U
1
∂x
2
1
+
∂
2
U
1
∂x
2
2
+
∂
2
U
1
∂x
2
3
+ ρg
1
, (5.109)
x
2
Component: ρ
∂U
2
∂t
+ U
2
∂U
2
∂x
1
+ U
2
∂U
2
∂x
2
+ U
3
∂U
2
∂x
3
= −
∂P
∂x
2
+ µ
∂
2
U
2
∂x
2
1
+
∂
2
U
2
∂x
2
2
+
∂
2
U
2
∂x
2
3
+ ρg
2
, (5.110)
x
3
Component: ρ
∂U
3
∂t
+ U
1
∂U
3
∂x
1
+ U
2
∂U
3
∂x
2
+ U
3
∂U
3
∂x
3
= −
∂P
∂x
3
+ µ
∂
2
U
3
∂x
2
1
+
∂
2
U
3
∂x
2
2
+
∂
2
U
3
∂x
2
3
+ ρg
3
. (5.111)
• Momentum Equations in Cylindrical Coordinates
– Momentum equations with τ
ij
terms:
r Component: ρ
*
∂U
r
∂t
+ U
r
∂U
r
∂r
+
U
ϕ
r
∂U
r
∂ϕ
−
U
2
ϕ
r
+ U
z
∂U
r
∂z
+
= −
∂P
∂r
−
1
r
∂
∂r
(rτ
rr
)+
1
r
∂τ
rϕ
∂ϕ
−
τ
ϕϕ
r
+
∂τ
rz
∂z
+ ρg
r
, (5.112)
ϕ Component: ρ
∂U
ϕ
∂t
+ U
r
∂U
ϕ
∂r
+
U
ϕ
r
∂U
ϕ
∂ϕ
+
U
r
U
ϕ
r
+ U
z
∂U
ϕ
∂z
= −
1
r
∂P
∂ϕ
−
1
r
2
∂
∂r
(r
2
τ
rϕ
)+
1
r
∂τ
ϕϕ
∂ϕ
+
∂τ
ϕz
∂z
+ ρg
ϕ
, (5.113)
z Component: ρ
∂U
z
∂t
+ U
r
∂U
z
∂r
+
U
ϕ
r
∂U
z
∂ϕ
+ U
z
∂U
z
∂z
= −
∂P
∂z
−
1
r
∂
∂r
(rτ
rz
)+
1
r
∂τ
ϕz
∂ϕ
+
∂τ
zz
∂z
+ ρg
z
. (5.114)
– Navier–Stokes equations for ρ and µ both being constant:
r Component: ρ
*
∂U
r
∂t
+ U
r
∂U
r
∂r
+
U
ϕ
r
∂U
r
∂ϕ
−
U
2
ϕ
r
+ U
z
∂U
r
∂
z
+
= −
∂P
∂r
+ µ
∂
∂r
1
r
∂
∂r
(rU
r
)
+
1
r
2
∂
2
U
r
∂ϕ
2
−
2
r
2
∂U
ϕ
∂ϕ
+
∂
2
U
r
∂z
2
+ ρg
r
,
(5.115)
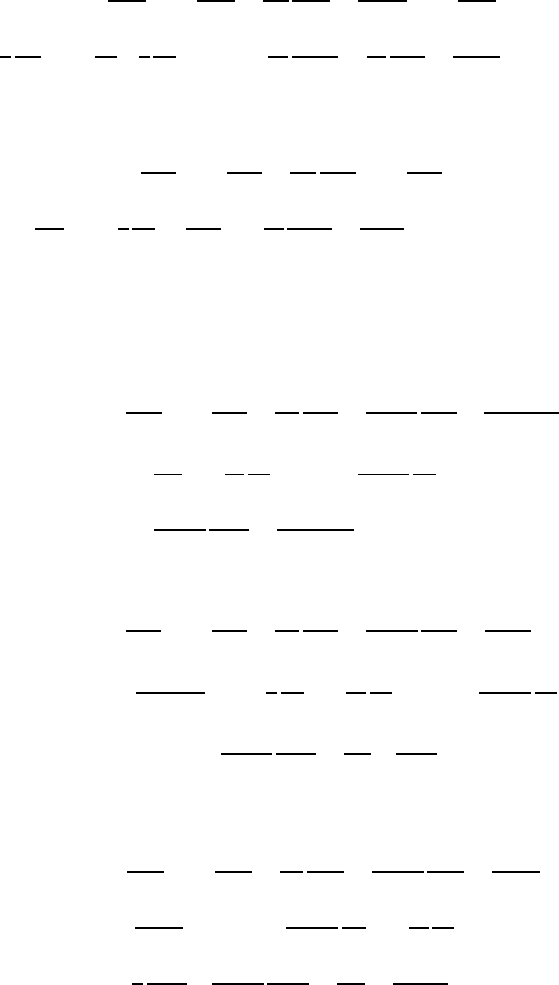
5.7 Basic Equations in Different Coordinate Systems 139
ϕ Component: ρ
∂U
ϕ
∂t
+ U
r
∂U
ϕ
∂r
+
U
ϕ
r
∂U
ϕ
∂ϕ
+
U
r
U
ϕ
r
+ U
z
∂U
ϕ
∂
z
= −
1
r
∂p
∂ϕ
+ µ
∂
∂r
1
r
∂
∂r
(rU
ϕ
)
+
1
r
2
∂
2
U
ϕ
∂ϕ
2
+
2
r
2
∂U
r
∂ϕ
+
∂
2
U
ϕ
∂z
2
+ ρg
ϕ
,
(5.116)
z Component: ρ
∂U
z
∂t
+ U
r
∂U
z
∂r
+
U
ϕ
r
∂U
z
∂ϕ
+ U
z
∂U
z
∂z
= −
∂P
∂z
+ µ
1
r
∂
∂r
r
∂U
z
∂r
+
1
r
2
∂
2
U
z
∂ϕ
2
+
∂
2
U
z
∂z
2
+ ρg
z
. (5.117)
• Momentum Equations in Spherical Coordinates
– Momentum equations with τ
ij
terms
r Component: ρ
*
∂U
r
∂t
+ U
r
∂U
r
∂r
+
U
θ
r
∂U
r
∂θ
+
U
φ
r sin θ
∂U
r
∂φ
−
U
2
θ
+ U
2
φ
r
+
= −
∂P
∂r
−
1
r
2
∂
∂r
(r
2
τ
rr
)+
1
r sin θ
∂
∂θ
(τ
rθ
sin θ)
+
1
r sin θ
∂τ
rφ
∂φ
−
τ
θθ
+ τ
θθ
r
+ ρg
r
,
(5.118)
θ Component: ρ
∂U
θ
∂t
+ U
r
∂U
θ
∂r
+
U
θ
r
∂U
θ
∂θ
+
U
φ
r sin θ
∂U
θ
∂φ
+
U
r
U
θ
r
−
U
2
φ
cot θ
r
+
= −
1
r
∂p
∂θ
−
1
r
2
∂
∂r
(r
2
τ
rθ
)+
1
r sin θ
∂
∂θ
(τ
θθ
sin θ)+
1
r sin θ
∂τ
θφ
∂φ
+
τ
rθ
r
−
cot θ
r
τ
φφ
+ ρg
θ
,
(5.119)
φ Component: ρ
∂U
φ
∂t
+ U
r
∂U
φ
∂r
+
U
θ
r
∂U
φ
∂θ
+
U
φ
r sin θ
∂U
φ
∂φ
+
U
φ
U
r
r
+
U
θ
U
φ
r
cot θ
= −
1
r sin θ
∂p
∂φ
−
1
r
2
∂
∂r
!
r
2
τ
rφ
"
+
1
r
∂τ
θφ
∂θ
+
1
r sin θ
∂τ
φφ
∂φ
+
τ
rφ
r
+
2cotθ
r
τ
θφ
+ ρg
φ
.
(5.120)

140 5 Basic Equations of Fluid Mechanics
• Navier–Stokes Equations for ρ and µ both being constant
r Component: ρ
*
∂U
r
∂t
+ U
r
∂U
r
∂r
+
U
θ
r
∂U
r
∂θ
+
U
φ
r sin θ
∂U
r
∂φ
−
U
2
θ
+ U
2
φ
r
+
= −
∂P
∂r
+ µ
∇
2
U
r
−
2
r
2
U
r
−
2
r
2
∂U
θ
∂θ
−
2
r
2
U
θ
cot θ
−
2
r
2
sin θ
∂U
φ
∂φ
+ ρg
r
, (5.121)
θ Component: ρ
∂U
θ
∂t
+ U
r
∂U
θ
∂r
+
U
θ
r
∂U
θ
∂θ
+
U
φ
r sin θ
∂U
θ
∂φ
+
U
r
U
θ
r
−
U
2
φ
cot θ
r
+
= −
1
r
∂P
∂θ
+ µ
∇
2
U
θ
+
2
r
2
∂U
r
∂θ
−
U
θ
r
2
sin
2
θ
−
2cosθ
r
2
sin
2
θ
∂U
φ
∂φ
+ ρg
θ
, (5.122)
φ Component: ρ
∂U
φ
∂t
+ U
r
∂U
φ
∂r
+
U
φ
r
∂U
φ
∂θ
+
U
φ
r sin θ
∂U
φ
∂φ
+
U
φ
U
r
r
+
U
θ
U
φ
r
cot θ
= −
1
r sin θ
∂P
∂φ
+ µ
∇
2
U
φ
−
U
φ
r
2
sin
2
θ
+
2
r
2
sin
2
θ
∂U
r
∂φ
+
2cosθ
r
2
sin
2
θ
∂U
θ
∂φ
+ ρg
φ
. (5.123)
In these equations the operator ∇
2
corresponds to:
∇
2
=
1
r
2
∂
∂r
r
2
∂
∂r
+
1
r
2
sin θ
∂
∂θ
sin θ
∂
∂θ
+
1
r
2
sin
2
θ
∂
2
∂φ
2
. (5.124)
• Components of the molecular momentum transport tensor in Cartesian
coordinates
τ
11
= −µ
2
∂U
1
∂x
1
−
2
3
(
∂U
k
∂x
k
)
; τ
22
= −µ
2
∂U
2
∂x
2
−
2
3
(
∂U
k
∂x
k
)
,
τ
33
= −µ
2
∂U
3
∂x
3
−
2
3
(
∂U
k
∂x
k
)
, (5.125)
τ
12
= τ
21
= −µ
∂U
1
∂x
2
+
∂U
2
∂x
1
,τ
23
= τ
32
= −µ
∂U
2
∂x
3
+
∂U
3
∂x
2
,
τ
31
= τ
13
= −µ
∂U
3
∂x
1
+
∂U
1
∂x
3
. (5.126)
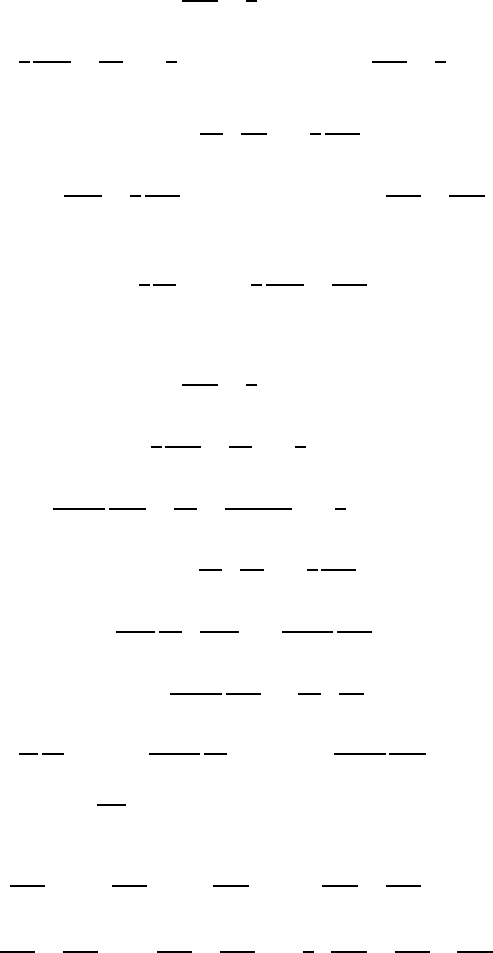
5.7 Basic Equations in Different Coordinate Systems 141
• Components of the molecular m on in time transport tensor in cylindrical
coordinates
τ
rr
= −µ
2
∂U
r
∂r
−
2
3
(∇·U)
,
τ
ϕϕ
= −µ
2
1
r
∂U
ϕ
∂ϕ
+
U
r
r
−
2
3
(∇·U)
,τ
zz
= −µ
2
∂U
z
∂x
z
−
2
3
(∇·U)
,
(5.127)
τ
rϕ
= τ
ϕr
= −µ
r
∂
∂r
U
ϕ
r
+
1
r
∂U
r
∂ϕ
,
τ
ϕz
= τ
zϕ
= −µ
∂U
ϕ
∂z
+
1
r
∂U
z
∂ϕ
,τ
zr
= τ
rz
= −µ
∂U
z
∂r
+
∂U
r
∂z
,
(5.128)
with
(∇·U )=
1
r
∂
∂r
(rU
r
)+
1
r
∂U
ϕ
∂ϕ
+
∂U
z
∂z
. (5.129)
• Components of the molecular momentum transport tensor in spherical
coordinates
τ
rr
= −µ
2
∂U
r
∂r
−
2
3
(∇·U)
, (5.130)
τ
θθ
= −µ
2
1
r
∂U
θ
∂θ
+
U
r
r
−
2
3
(∇·U)
, (5.131)
τ
φφ
= −µ
2
1
r sin θ
∂U
φ
∂φ
+
U
r
r
+
U
θ
cot θ
r
−
2
3
(∇·U)
, (5.132)
τ
rθ
= τ
θr
= −µ
r
∂
∂r
U
θ
r
+
1
r
∂U
r
∂θ
, (5.133)
τ
θφ
= τ
φθ
= −µ
sin θ
r
∂
∂θ
U
φ
sin θ
+
1
r sin θ
∂U
θ
∂φ
, (5.134)
τ
φr
= τ
rφ
= −µ
1
r sin θ
∂U
r
∂φ
+ r
∂
∂r
U
φ
r
, (5.135)
(∇·U)=
1
r
2
∂
∂r
(r
2
U
r
)+
1
r sin θ
∂
∂θ
(U
θ
sin θ)+
1
r sin θ
∂U
φ
∂φ
. (5.136)
• Dissipation function τ
ij
∂U
j
∂x
i
= µΦ
µ
Cartesian coordinates:
Φ
µ
=2
3
∂U
1
∂x
1
2
+
∂U
2
∂x
2
2
+
∂U
3
∂x
3
2
4
+
∂U
2
∂x
1
+
∂U
1
∂x
2
2
+
∂U
3
∂x
2
+
∂U
2
∂x
3
2
+
∂U
1
∂x
3
+
∂U
3
∂x
1
2
−
2
3
∂U
1
∂x
1
+
∂U
2
∂x
2
+
∂U
3
∂x
3
2
.
(5.137)
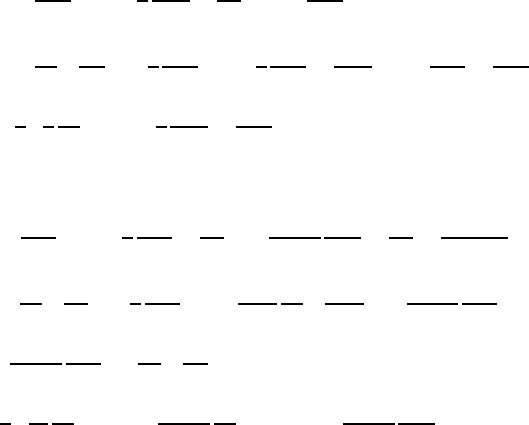
142 5 Basic Equations of Fluid Mechanics
Cylindrical coordinates:
Φ
µ
=2
3
∂U
r
∂r
2
+
1
r
∂U
ϕ
∂ϕ
+
U
r
r
2
+
∂U
z
∂x
z
2
4
+
r
∂
∂r
U
ϕ
r
+
1
r
∂U
z
∂ϕ
2
+
1
r
∂U
z
∂ϕ
+
∂U
ϕ
∂x
z
2
+
∂U
r
∂x
z
+
∂U
z
∂r
2
−
2
3
1
r
∂
∂r
(rU
r
)+
1
r
∂U
ϕ
∂ϕ
+
∂U
z
∂x
z
2
. (5.138)
Spherical coordinates:
Φ
µ
=2
3
∂U
r
∂r
2
+
1
r
∂U
θ
∂θ
+
U
r
r
2
1
r sin θ
∂U
φ
∂φ
+
U
r
r
+
U
θ
cot θ
r
2
4
+
r
∂
∂r
U
θ
r
+
1
r
∂U
r
∂θ
2
+
sin θ
r
∂
∂θ
U
φ
sin θ
+
1
r sin θ
∂U
θ
∂φ
2
+
1
r sin θ
∂U
r
∂φ
+ r
∂
∂r
U
φ
r
2
−
2
3
1
r
2
∂
∂r
(r
2
U
r
)+
1
r sin θ
∂
∂θ
(U
θ
sin θ )+
1
r sin θ
∂U
φ
∂φ
2
.
(5.139)
The above equations can be solved in connection with the initial and
boundary conditions describing the actual flow problems. Very often the
boundary conditions define the coordinate system chosen for solving a
particular flow problem.
5.8 Special Forms of the Basic Equations
Due to the multitude of fluid mechanical considerations, special forms of the
equations have crystallized out of those treated in the preceding sections.
Some of these equations will be derived and also explained in this section.
These are the vorticity equation, the Bernoulli equation and the Crocco equa-
tion, some of which have already been treated. The following derivations
will also treat the Kelvin theorem as a basis for explanations of its physical
significance. The objective of the considerations is to bring out clearly the
prerequisites under which the derived special forms of the basic equations are
valid. Only when a sound basis for the simplified treatments of flow problems
exists can the special forms of the basic equations lead to valuable results. In
case the insight into a particular flow is not present, the general form of the
basic equations of fluid mechanics should be employed to slove the considered
flow problems.
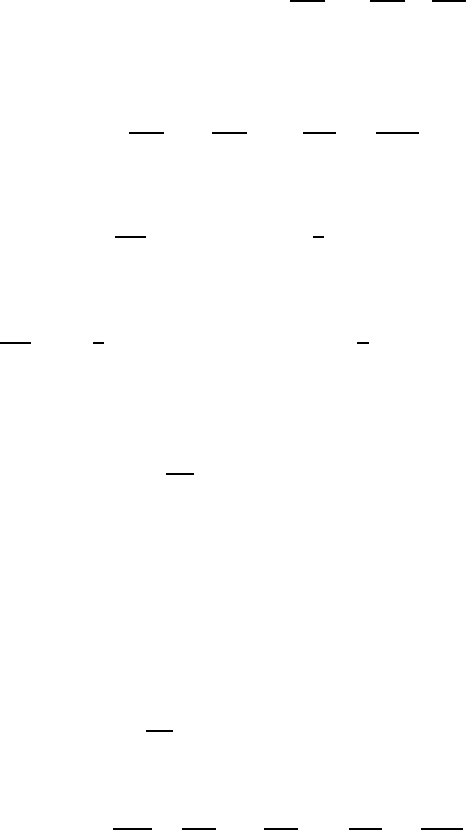
5.8 Special Forms of the Basic Equations 143
5.8.1 Transport Equation for Vorticity
The vorticity ω
i
is a local property of the flow field which can be employed ad-
vantageously in considerations of rotating fluid motions. It can be computed
from the velocity field as follows:
2ω
k
= ∇×U = −
ijk
∂U
j
∂x
i
=
∂U
j
∂x
i
−
∂U
i
∂x
j
. (5.140)
For a fluid with the properties ρ = constant and µ = constant, the Navier–
Stokes equation can be written in the following way:
ρ
∂U
j
∂t
+ U
i
∂U
j
∂x
i
= −
∂P
∂x
j
+ µ
∂
2
U
j
∂x
2
i
+ ρg
j
, (5.141)
or in vector form:
∂U
∂t
+(U ·∇) U
= −
1
ρ
∇P + ν∇
2
U + g. (5.142)
This vector form of the Navier–Stokes equation can also be written as:
∂U
∂t
+ ∇
1
2
U · U
− U × (∇×U )=−
1
ρ
∇P + ν∇
2
U + g. (5.143)
When one applies the operator ∇×(...) to each of the terms appearing
in the above equation, one obtains:
∂ω
∂t
−∇×(U × ω)=ν∇
2
ω. (5.144)
Making use of the following relationship, valid for vectors:
∇×(U × ω)=U(∇·ω) − ω(∇·U) − (U ·∇)ω +(ω ·∇)U,
where ∇·ω = 0 as the divergence of the rotation of each vector is equal to
zero, and where at the same time ρ = constant and also ∇·U =0holds
due to the continuity equation. When one introduces all this into the above
equations, the transport equation for vorticity results:
∂ω
∂t
+(U ∇)ω =(ω∇)U + ν∇
2
ω, (5.145)
or written in tensor notation:
Dω
j
Dt
=
∂ω
j
∂t
+ U
i
∂ω
j
∂x
i
= ω
j
∂U
i
∂x
j
+ ν
∂
2
ω
j
∂x
2
i
. (5.146)
Equation (5.146) does not contain the pressure term, hence it is apparent
that the vorticity field can be determined without knowledge of the pressure
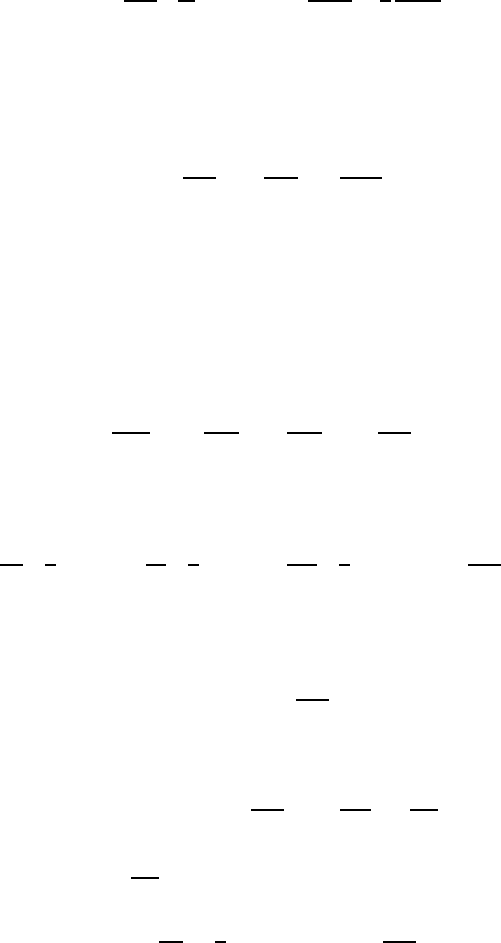
144 5 Basic Equations of Fluid Mechanics
distribution. To be able to compute the pressure, one forms the divergence
of the Navier–Stokes equation and obtains for g
j
=0:
∂
2
∂x
2
i
P
ρ
= ω
2
j
+ U
j
∂
2
U
j
∂x
2
i
−
1
2
∂
2
U
2
j
∂x
2
i
, (5.147)
thus yielding a Poisson equation for the computation of the pressure. For
two-dimensional flows, for which the vorticity vector stands vertical on the
plane of the flow, (ω ·∇)U = 0. The transport equation for the vorticity
therefore reads:
∂ω
j
∂t
+ U
i
∂ω
j
∂x
i
= ν
∂
2
ω
j
∂x
2
i
. (5.148)
5.8.2 The Bernoulli Equation
The general momentum equations can be transferred into the Euler equations
by assuming a fluid mechanically ideal fluid to exist. This is the equation with
which to start to derive the Bernoulli equation:
ρ
DU
j
Dt
= ρ
∂U
j
∂t
+ U
i
∂U
j
∂x
i
= −
∂P
∂x
j
+ ρg
j
. (5.149)
Multiplying this equation by U
j
, one obtains the mechanical energy
equation valid for dissipation-free fluid flows:
ρ
D
Dt
1
2
U
2
j
= ρ
∂
∂t
1
2
U
2
j
+ U
i
∂
∂x
i
1
2
U
2
j
= −U
j
∂P
∂x
j
+ ρg
j
U
j
.
(5.150)
When one introduces the potential field G for the presentation of g
j
as follows:
g
j
= −
∂G
∂x
j
, (5.151)
the last term of (5.151) reads:
ρg
j
U
j
= −ρU
j
∂G
∂x
j
= −ρ
DG
Dt
+ ρ
∂G
∂t
, (5.152)
and one obtains for
∂G
∂t
=0:
ρ
D
Dt
1
2
U
2
j
+ G
= −U
j
∂P
∂x
j
. (5.153)
