Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

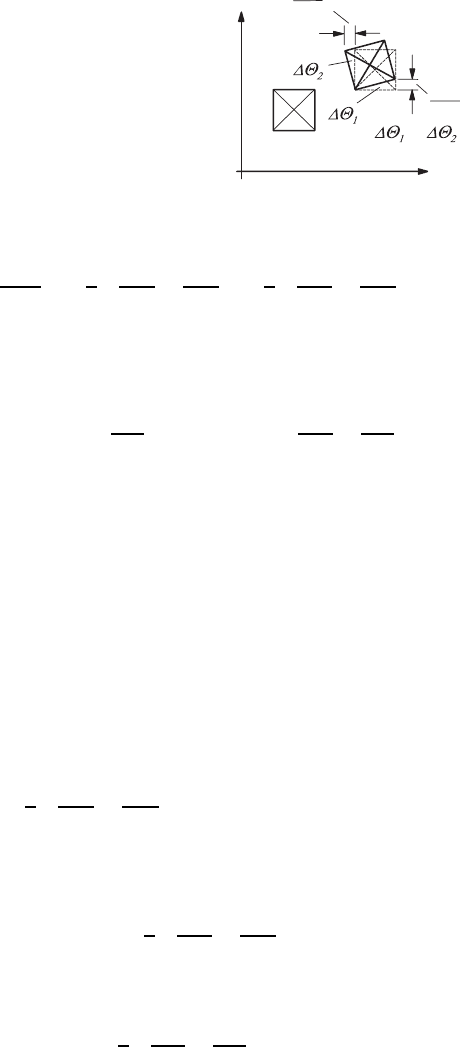
4.5 Translation, Deformation and Rotation of Fluid Elements 105

Fig. 4.11 Translation and rotation of

a ﬂuid element in a ﬂow ﬁeld, due to

velocity gradients

= x

∂

(

∆

)

∆

ℜ

∂

(

∆

)

∆

ℜ

Pur rotation



dΘ





dΘ





∂U

∂x

−

∂U

∂x



(4.96)

Generally, the components of the rotational velocity vector {ω

} for the lo-

cally occurring rotation of a ﬂuid element per unit time can be stated as

follows:

rot(U )=

ijk

∂U

∂x

=2ω

∂U

∂x

−

∂U

∂x

(4.97)

The quantity ω

represents the double rotational speed around the axis of

the ﬂuid element, with the rotation occurring in the positive direction. The

second diagonal of the considered ﬂuid element in Fig. 4.11 rotates with the

same angular speed. {ω

} is an important kinematic quantity of the velocity

ﬁeld. It is deﬁned mathematically as vorticity and is computed as half the

rotational speed of the velocity ﬁeld. Thus ω

,t) is a ﬁeld quantity of its

own, for which we can easily show that ω

,t) = 0 when a ﬂow ﬁeld is free of

rotation. When ω

,t) = 0, ﬂows subjected to rotations are present, whose

rotational properties can best be studied when expressing the conservation

laws for mass, impulse and energy in terms of ω

When one considers next the angular deformation of a ﬂuid element shown

in Fig. 4.12, one can see that for the angle deformation the following holds:



dΘ

−

dΘ



deformation angular speed

Thus for the angular deformation in the plane x

−x

the following expression

holds:



∂U

∂x

∂U

∂x



(4.98)

or, considering the angular deformation only,



∂U

∂x

∂U

∂x



i = j (4.99)

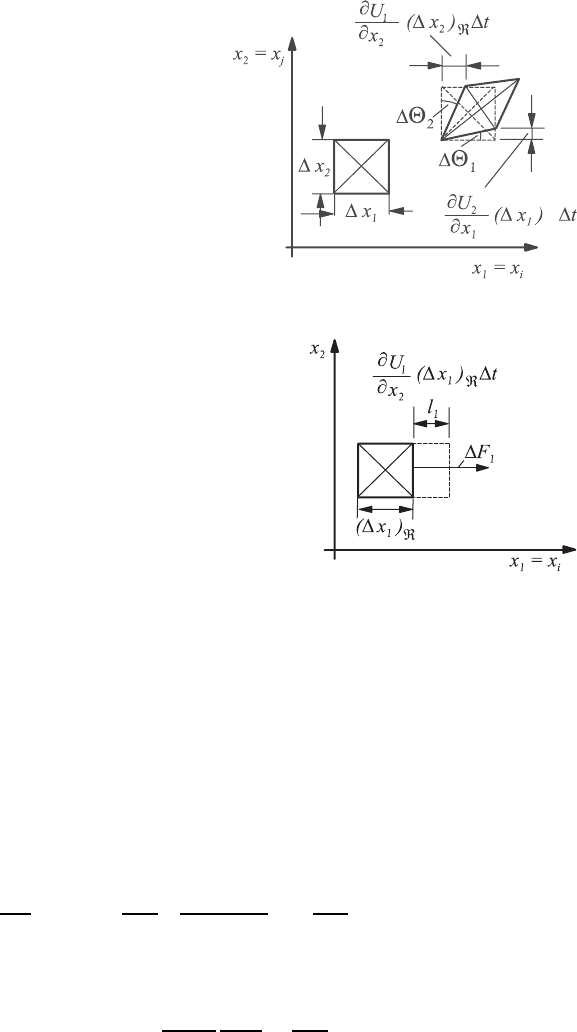
106 4 Basics of Fluid Kinematics

Fig. 4.12 Translation and angle de-

formation of a ﬂuid element in a ﬂow

ﬁeld due to velocity gradients

Fig. 4.13 Elongation of a volume element due

to velocity gradients in the ﬂow ﬁeld

Analogous to considerations in solid-state mechanics, the symmetry of the

deformation tensor holds:

(4.100)

Finally, one has to consider the dilatation of a ﬂuid element which experiences

strain rates due to the velocity gradient existing in a ﬂow ﬁeld, as is shown

in Fig. 4.13. The linear deformation in length that occurs due to an existing

velocity gradient in the direction x

can be stated as follows:

= lim

∆t→0



∂U

∂x



(∆x

)



∆t



∂U

∂x



(∆x

)



(4.101)

From this, the linear deformation that occurs per unit length and unit time

is computed:

(∆x

)

d(l

)

∂U

∂x

(4.102)

4.5 Translation, Deformation and Rotation of Fluid Elements 107

On multiplying the linear deformation by the area perpendicular to the x

axis, the corresponding volume change results:

d(δV

)





∂U

∂x



(δV

)



(4.103)

The same considerations hold for the x

and x

axes also. Summed over all

three axis directions, one obtains for the entire volume change per unit time

(δV )



d(δV )



∂U

∂x

(4.104)

i.e. the divergence of the velocity ﬁeld indicates how the volume of a ﬂuid

element changes with time at a point in space. This was already shown in

Sect. 4.3.

It is customary in the literature to combine elongations of ﬂuid elements

and their angular deformations with a deformation tensor in such a way that



∂U

∂x

∂U

∂x



(4.105)

so that for the deformation tensor

{ε

} =

⎧

⎨

⎩

⎫

⎬

⎭

and ε

= ε

(4.106)

From the above considerations, the following relationship results:

∂U

∂x



∂U

∂x

∂U

∂x





∂U

∂x

−

∂U

∂x



(4.107)

i.e. the following kinematic relationship exists:

∂U

∂x

= ε

dΘ

= ε



ijk

∂U

∂x

(4.108)

Hence the gradients that existing in velocity ﬁelds are linked to deformations

and rotations of ﬂuid elements, the gradients yields corresponding rates of

deformation and rotational angular velocities. This has to be taken into con-

sideration when employing the analogy between solid-state mechanics and

ﬂuid mechanics. It is necessary to transfer considerations of deformations of

elastic bodies, carried out in solid-state mechanics, to rates of deformation

of ﬂuid elements occurring in ﬂuid mechanics. The latter occur due to gradi-

ents existing in velocity ﬁelds and the former due to existing internal surface

forces.

108 4 Basics of Fluid Kinematics

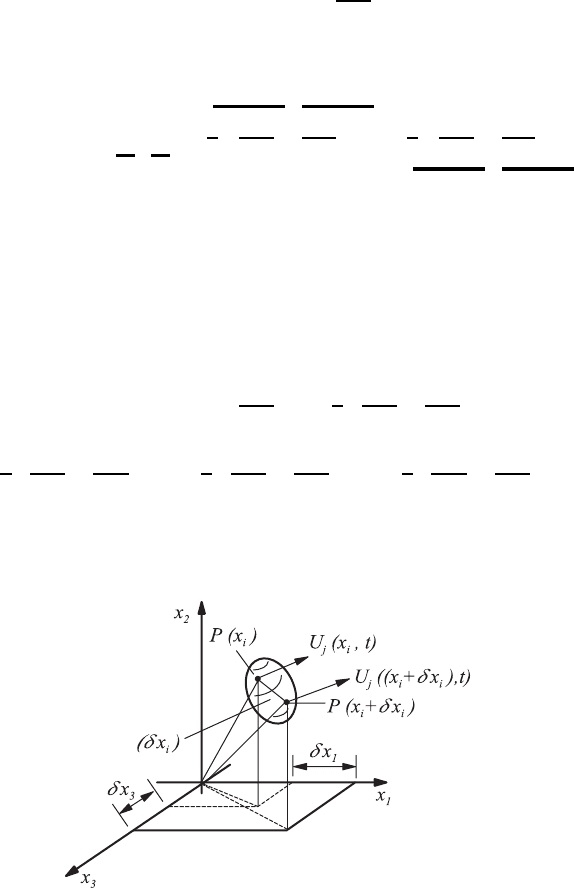
4.6 Relative Motions

Considerations of the velocities at two points separated by (δx

)resultinthe

following relationship if one applies Taylor series expansion:

+ δx

,t)=U

,t)+

∂U

∂x

δx

+ ··· (4.109)

or the relationship can be rewritten as follows:

+ δx

,t)= U

,t)



 

Translation

Rotation

  



∂U

∂x

−

∂U

∂x



δx



∂U

∂x

∂U

∂x



δx

  

Deformation

(4.110)

For further details, see Aris [4.5]. Considering the various terms in this rela-

tionship makes it clear that the velocity at the point adjacent to x

, i.e. at

the point x

+ δx

, is composed of the translation by velocity at point P (x

a rotational velocity around this point and a deformation action in this point

(Fig. 4.14). The components for j =1, 2, 3read

j =1: U

+ δx

,t)=

∂U

∂x

δx



∂U

∂x

−

∂U

∂x



δx



∂U

∂x

−

∂U

∂x



δx



∂U

∂x

∂U

∂x



δx



∂U

∂x

∂U

∂x



δx

(4.111)

Fig. 4.14 Relative motions in a ﬂuid element

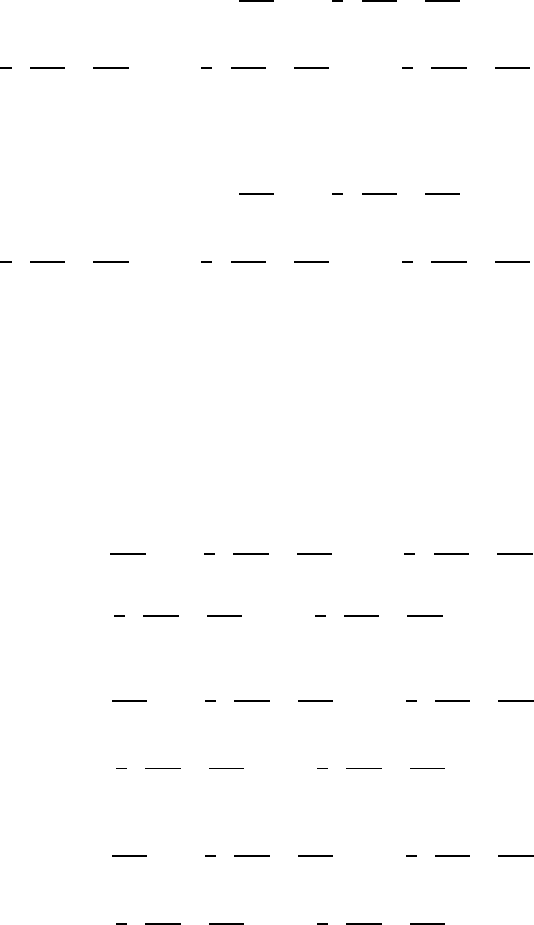
4.6 Relative Motions 109

j =2: U

+ δx

,t)=

∂U

∂x

δx



∂U

∂x

−

∂U

∂x



δx



∂U

∂x

−

∂U

∂x



δx



∂U

∂x

∂U

∂x



δx



∂U

∂x

∂U

∂x



δx

(4.112)

j =3: U

+ δx

,t)=

∂U

∂x

δx



∂U

∂x

−

∂U

∂x



δx



∂U

∂x

−

∂U

∂x



δx



∂U

∂x

∂U

∂x



δx



∂U

∂x

∂U

∂x



δx

(4.113)

With the above equations, most general motions of ﬂuid elements can now

be described, i.e. the motion at any point of a ﬂuid element can be stated as

the sum of the translation of a reference point, a rotational motion around

this point and an additional deformation. The motion is due to translation

and rotation and a superimposed deformation.

The diﬀerent components of the equations (4.111) to (4.113) can be

obtained by regrouping as follows:

j =1: U

∂U

∂x

δx



∂U

∂x

∂U

∂x



δx



∂U

∂x

∂U

∂x



δx





∂U

∂x

−

∂U

∂x



δx



∂U

∂x

−

∂U

∂x



δx



(4.114)

j =2: U

∂U

∂x

δx



∂U

∂x

∂U

∂x



δx



∂U

∂x

∂U

∂x



δx





∂U

∂x

−

∂U

∂x



δx



∂U

∂x

−

∂U

∂x



δx

(4.115)

j =3: U

∂U

∂x

δx



∂U

∂x

∂U

∂x



δx



∂U

∂x

∂U

∂x



δx





∂U

∂x

−

∂U

∂x



δx



∂U

∂x

−

∂U

∂x



δx

(4.116)

The expressions in front of the square brackets represent the translational

velocity, which is given by the following velocity vector:

,t)={U

}

(4.117)

110 4 Basics of Fluid Kinematics

In the square brackets the product of the deformation tensor:

,t)=

⎧

⎪

⎨

⎪

⎩

∂U

∂x



∂U

∂x

∂U

∂x





∂U

∂x

∂U

∂x





∂U

∂x

∂U

∂x



∂U

∂x



∂U

∂x

∂U

∂x





∂U

∂x

∂U

∂x





∂U

∂x

∂U

∂x



∂U

∂x

⎫

⎪

⎬

⎪

⎭

(4.118)

and of the “distance vector” from point x

to (x

+ δx

{δx

} = {δx

,δx

} (4.119)

is shown, and in the curly brackets the vector product of

{δx

} = {δx

,δx

} (4.120)

and

2ω



∂U

∂x

−

∂U

∂x



;



∂U

∂x

−

∂U

∂x



;



∂U

∂x

−

∂U

∂x



(4.121)

is shown. Hence the entire motion can be written as

(x +dx

,t)=U

,t)+D

,t)δx

+ ε

ijk

,t)δx

(4.122)

This relationship again expresses the fact that the total motion of a point



+dx

) can be understood as the translational motion of the point P (x

Dilatation

Translation

and deformation

Angle deformation

Rotation

Fig. 4.15 Illustration of the translational motion, the deformation and the rotation

of a ﬂuid element

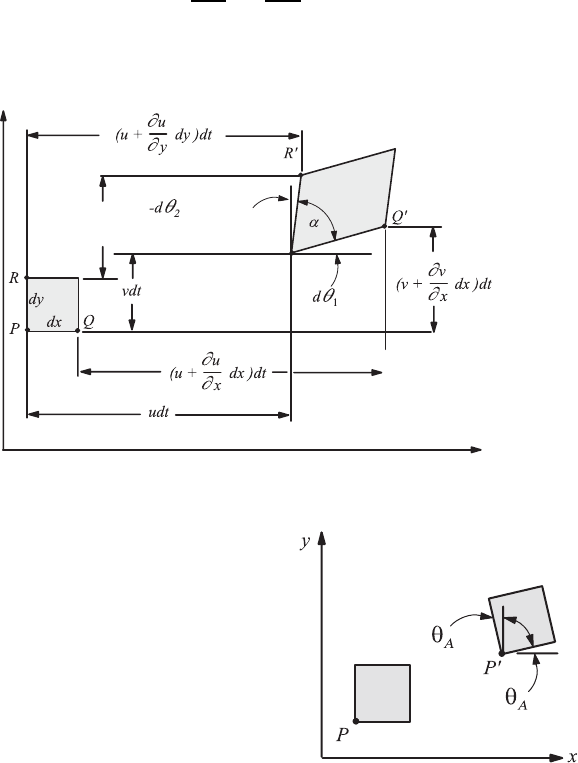
4.6 Relative Motions 111

superimposed by deformation motions and rotational motions around P (x

)

(Fig. 4.14).

The diﬀerent parts, i.e the translation, deformation and rotation, can be

taken from the sequence of a ﬂuid element which is shown in Fig. 4.15. For the

two-dimensional case with U

= u and U

= v and with x

= x and x

= y,

the considerations for the diﬀerent subjects are shown once more in Fig. 4.16.

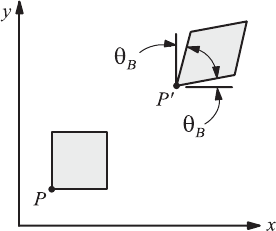
In Fig. 4.17 a ﬂuid element is shown under translation and pure rotation

once again. Fig. 4.18, on the other hand, shows a ﬂuid element carrying out

a translation motion in the presence of a pure deformation, i.e. without the

presence of a rotation. The last manner of motion requires

∂U

∂x

∂U

∂x

(4.123)

so that ω

=0.

Fig. 4.16 Translation, deformation and rotation of a ﬂuid element due to the

velocity components u and v

Fig. 4.17 Translation motion of a ﬂuid ele-

ment with rotation

112 4 Basics of Fluid Kinematics

Fig. 4.18 Translation motion of a ﬂuid ele-

ment with deformation

References

4.1. Brodkey, R.S., The Phenomena of Fluid Motions, Dover, New York, 1967.

4.2. Spurk, J.H., Fluid Science/Technology: An Introduction to the Theory of Fluids,

Springer, Berlin Heidelberg New York, 1966.

4.3. Hutter, K., Fluid Dynamics and Thermodynamics: An Introduction. Springer,

Berlin Heidelberg New York, 1995.

4.4. Currie, I.G., Fundamental Mechanics of Fluids, McGraw-Hill, New York, 1974.

4.5. Aris, R., Vectors, Tensors and the Basic Equations of Fluid Mechanics, McGraw-

Hill, New York, 1974.

Chapter 5

Basic Equations of Fluid Mechanics

5.1 General Considerations

Fluid mechanics considerations are applied in many ﬁelds, especially in en-

gineering. Below a list is provided which clearly indicates the far-reaching

applications of ﬂuid-mechanics knowledge and their importance in various

ﬁelds of engineering. Whereas it was usual in the past to carry out special

ﬂuid mechanics considerations for each of the areas listed below, today one

strives increasingly at the development and introduction of generalized ap-

proaches that are applicable without restrictions to all of these ﬁelds. This

makes it necessary to derive the basic equations of ﬂuid mechanics so gener-

ally that they fulﬁll the requirements for the broadest applicability in areas

of science and engineering, i.e. in those areas indicated in the list below. The

objective of the derivations in this section is to formulate the conservation

laws for mass, momentum, energy, chemical species, etc., in such a way that

they can be applied to all the ﬂow problems that occur in the following areas:

• Heat exchanger, cooling and drying technology

• Reaction technology and reactor layout

• Aerodynamics of vehicles and aeroplanes

• Semiconductor-crystal production, thin-ﬁlm technology, vapor-phase

deposition processes

• Layout and optimization of pumps, valves and nozzles

• Use of ﬂow equipment parts such as pipes and junctions

• Development of measuring instruments and production of sensors

• Ventilation, heating and air-conditioning techniques, layout and tests,

laboratory vents

• Problem solutions for roof ventilation and ﬂows around buildings

• Production of electronic components, micro-systems analysis engineering

• Layout of stirrer systems, propellers and turbines

• Sub-domains of biomedicine and medical engineering

• Layout of baking ovens, melting furnaces and other combustion units

113

114 5 Basic Equations of Fluid Mechanics

Total mass of

considered fluid

Fig. 5.1 Division of a ﬂuid into  ﬂuid elements for mass conservation considerations

• Development of engines, catalyzers and exhaust systems

• Combustion and explosion processes, energy generation, environmental

engineering

• Sprays, atomizing and coating technologies

Concerning the formulation of the basic equations of ﬂuid mechanics, it is easy

to formulate the conservation equations for mass, momentum, energy and

chemical species for a ﬂuid element, see Fig. 5.1, i.e. to derive the “Lagrange

form” of the equations. In this way, the derivations can be represented in

an easily comprehensible way and it is possible to build up the derivations

upon the basic knowledge of physics. Derivations of the basic equations in

the “Lagrange form” are usually followed by transformation considerations

whose aim is to derive local formulations of the conservation equations and

to introduce ﬁeld quantities into the mathematical representations, i.e. the

“Euler form” of the conservation equations is sought for solutions of ﬂuid

ﬂow problems. This requires one to express temporal changes of substantial

quantities as temporal changes of ﬁeld quantities, which makes it necessary,

partly, to repeat in this section the considerations in Chap. 2 but to explain

them in a somewhat diﬀerent and even deeper way.

The considerations to be carried in the sections below start out with the

assumption that, at a certain point in time t = 0, the mass of a ﬂuid is

subdivided into ﬂuid elements of the mass δm



, i.e.

M =





δm



Each ﬂuid element δm



is chosen to be large enough to make the assumption

δm



= constant possible, with suﬃcient precision, in spite of the molecular

structure of the ﬂuid. The assumption is also made to allow one to assign ar-

bitrary thermodynamic and ﬂuid mechanics properties α



(t),t)=α



(t)

to a ﬂuid element to yield α



= constant, with satisfactory precision for ﬂuid

mechanics considerations.

The term α



,t), with x



= x



(t), expresses the fact that the ther-

modynamic or ﬂuid mechanics property, which is assigned to the considered

ﬂuid element, represents a substantial quantity that is only a function of time.

This property of the element changes with time at a ﬁxed position in space,

but changes also due to the motion of the ﬂuid element. For the description