Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

4.4 Kinematic Quantities of Flow Fields 95

(

)

const

Velocity vector

Stream line

cons

)

(

)

Fig. 4.6 Sketch for clarifying the deﬁning equation for the stream line of a ﬂow ﬁeld

When one considers the deﬁning equation (4.46) for the stream line of a

two-dimensional ﬂow ﬁeld, it becomes understandable that, in general, for

each moment in time t,theratioofU

to U

is a function of x

and x

The resulting diﬀerential equation has to be solved in order to derive the

ﬂuid equation for the stream line. This will be explained on the basis of an

example that starts from the following two-dimensional velocity ﬁeld:

= x

(1 + 2t),U

= x

= 0 (4.47)

Introduced into the deﬁning equation (4.46) for the stream line, one obtains

d(x

)

d(x

)

(1 + 2t)

(4.48)

or, rewritten in the following form:

d(x

)

d(x

)

1+2t

(4.49)

By integration, the following relationship for (x

)

and (x

)

results:

ln(x

)

= C +

1+2t

ln(x

)

(4.50)

Considering the stream line, passing at time t = 0 the point (1, 1, 0), C =0

results and thus one can describe the stream line:

)

=[(x

)

]

(

1+2t

)

(4.51)

In the case that a three-dimensional velocity ﬁeld is considered, the above

derivations, which were carried out for the projection of the stream lines into

the planes x

−x

, can be performed in an analogous way. For the projections

96 4 Basics of Fluid Kinematics

into the planes x

−x

and x

−x

, relations analogous to the above used

deﬁning equation result:

d(x

)

d(x

)

(4.52)

d(x

)

d(x

)

(4.53)

Hence the deﬁning equations of the stream lines of a velocity ﬁeld can be

stated as follows:

d(x

)

d(x

)

d(x

)

d(x

)

d(x

)

d(x

)

(4.54)

or rewritten as:

d(x

)

d(x

)

d(x

)

(4.55)

These diﬀerential equations for the stream line of a velocity ﬁeld hold at each

moment in time t. Their solution leads to a relationship (x

)

= ψ(x

which describe a curve in space, the three-dimensional stream line.

Probably the simplest way to solve the set of diﬀerential equations (4.55)

is to seek a parameter solution (x

)

= x

(s), where s is a parameter that

varies along a streamline. The value of s at a certain reference point of the

ﬂow line is equal to zero. From there on it adopts increasing values along the

ﬂow line and in the ﬂow direction. For all values −∞ <s<∞ apresentation

oftheentirestreamlineisobtained.

By introducing s,oneobtains:

d(x

)

= U

,t)fort = constant and j = s (4.56)

a relationship which represents, for each coordinate (x

)

,adiﬀerentialequa-

tion and for j = 1, 2, 3 describing the stream lines in space for t = constant.

If the ﬂow line passing through the space point [x

]

at time t is sought, s =0

results from integrating the three diﬀerential equations, when x

(t)=x

j,0

then s = 0 is set. From this results the entire stream-line ﬁeld as:

)

= ψ

0,j

,t,s) (4.57)

In order to demonstrate the above approached to obtaining the three-

dimensional stream-line ﬁelds, the following velocity ﬁeld is considered again:

= x

(1 + t),U

= −x

t (4.58)

A set of three diﬀerential equations for the stream lines of this velocity ﬁeld

results:

4.4 Kinematic Quantities of Flow Fields 97

d(x

)

= x

(1 + t),

d(x

)

= −x

d(x

)

= −x

t (4.59)

Integration of these equations yields

)

= C

exp[(1 + t)s]

)

= C

exp[−s] (4.60)

)

= C

exp[−txs]

Searching for the stream line that passes through the point (1, 1, 1), one can

choose this point as reference point and set s =0for(x

)

=1.Fromthis

one obtains the integration constants:

= C

= 1 (4.61)

Hence the following results for (x

)

are obtained:

)

=exp[(1+t)s]

)

=exp[−s] (4.62)

)

=exp[−ts]

For time t = 0, a stream line path results:

)

=exp[s], (x

)

=exp[−s], (x

)

= 1 (4.63)

Hence one obtains for t = 0 a stream line passing in the plane x

=1,that

is described by

)

(4.64)

The entire stream line ﬁeld is obtained if one introduces for s =0arbi-

trary position coordinates (x

0,i

) so that for any the position coordinates the

following solution holds:

)

=(x

)

ψ,0

exp[(1 + t)s]

)

=(x

)

ψ,0

exp[−s] (4.65)

)

=(x

)

ψ,0

exp[−txs]

This set of equations indicates at each time t, the stream lines passing through

the point {x

}

ψ,0

, see Fig. 4.7. There the parameter s is zero and for all other

points of the considered stream line a value diﬀerent to zero exists. This

clear assignment is thus occurring which guarantees that stream lines never

intersect, as otherwise two velocities would exist simultaneously at this point

of intersection. This is precluded because of the existence of a well deﬁned

velocity ﬁelds (except for stagnation points and singularities).

In the preceding section, it was emphasized that, in general, stream lines,

path lines and streak lines are not identical and the computed examples

have conﬁrmed this. For stationary ﬂows all three lines are identical and are

characteristic for each considered ﬂow, i.e.

98 4 Basics of Fluid Kinematics

(1,1,1)

Path line

Streak line

Stream line

Fig. 4.7 Comparison of stream lines, path lines and streak lines

• For stationary ﬂow ﬁelds marked ﬂuid elements move along stream lines,

i.e. stream lines are equal to their corresponding path lines

• For stationary ﬂow ﬁelds stream lines can be made visible by locally

injected tracer particles, i.e. stream lines are equal to streak lines

As already said, for non-stationary ﬂows the corresponding stream lines, path

lines and streak lines are diﬀerent space curves, see Fig. 4.8.

4.4.2 Stream Function and Stream Lines

of Two-Dimensional Flow Fields

For two-dimensional incompressible velocity ﬁelds {U

} = {U

, 0},the

stream function can be introduced as a ﬁeld quantity. It is deﬁned as fol-

lows, i.e the velocity components are thus deﬁned as gradients of the stream

function:

∂ψ

∂x

and U

= −

∂ψ

∂x

(4.66)

Hence the stream function can be computed from the velocity ﬁeld by the

following line integral:

ψ −ψ

2,0

for x

= constant (4.67)

4.4 Kinematic Quantities of Flow Fields 99

= const

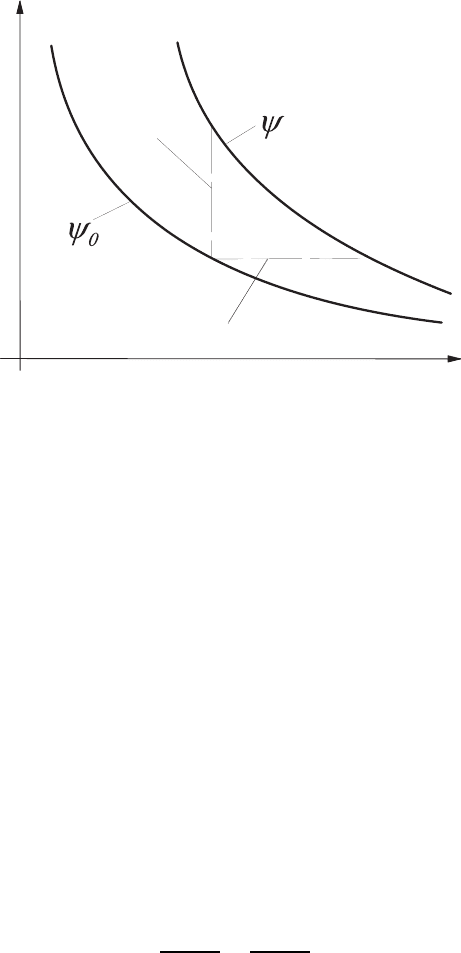
Fig. 4.8 Explanation of the deﬁning equations of stream function

or also

ψ −ψ

= −

1,0

for x

= constant (4.68)

The above equations show that the diﬀerence that exists between the val-

ues of two stream functions is a measure of the volume ﬂow rate that ﬂows

between two lines, each line corresponding to a constant stream function

value. The depth of the considered area is taken as 1 perpendicular to the

plane x

−x

. Accordingly the integrations along the line in (4.67) and (4.68)

drawninFig.4.8andstatedintheequationsforx

= constant and for

= constant, yield identical volume-ﬂow values, when the upper integra-

tion limits x

and x

are chosen such that the diﬀerences ψ −ψ

are equally

large in both integrals. For a ﬂuid with ρ = constant, i.e. for a thermodynam-

ically ideal ﬂuid, the identity of the integrals represents a mass-conservation

relationship. When one carries out the integrations stated in (4.67) and (4.68)

along a line ψ = constant i.e. for dψ =0,oneobtains

d(x

)

= U

d(x

)

(4.69)

or rewritten

d(x

)

d(x

)

(4.70)

From (4.70) it can be said by comparison with the deﬁnition equation for

the stream line stated in (4.46) that the stream function deﬁned for two-

dimensional ﬂow ﬁelds yields stream lines ψ for ψ = constant.

Whereas for the kinematic considerations, e.g. in Chap. 2, arbitrary math-

ematical relationships for the velocity ﬁeld could be used, the introduction of

100 4 Basics of Fluid Kinematics

the stream function requires a limitation of the considerations to those veloc-

ity ﬁelds which have to fulﬁll physical conditions. Considerations in Chap. 5

show that physically existing ﬂow ﬁelds have to fulﬁll the mass-conservation

law, which can be formulated for ideal ﬂuids (ρ = constant) as follows:

∂U

∂x

∂U

∂x

∂U

∂x

∂U

∂x

= 0 (4.71)

The stream function fulﬁlls the mass-conservation law for two-dimensional

ﬂows automatically and can easily be checked by inserting the deﬁnition of

ψ = in equation (4.66) and applying the Schwarz rule of diﬀerentiation.

When a prescribed velocity ﬁeld does not fulﬁll the mass-conservation

law, the integrations to be carried out according to (4.67) and (4.68) result

in solutions that contradict one another. This can be shown for the two-

dimensional ﬂow ﬁeld shown in Sect. 4.3.1 which does not fulﬁll the mass-

conservation law (i.e. the continuity equation):

= x

(1 + 2t),U

= 0 (4.72)

When one carries out the integration stated in (4.67), one obtains from the

deﬁning equations for the stream function, i.e. from (4.66) it results that:

∂ψ

∂x

= x

and

∂ψ

∂x

= −x

(1 + 2t) (4.73)

By integration of these equations, one obtains for the stream function:

ψ = x

+ F (x

,t),ψ= −x

(1 + 2t)+G(x

,t) (4.74)

or, expressed otherwise,

+ F (x

,t) = −x

(1 + 2t)+G(x

,t) (4.75a)

2(t +1)x

= G(x

,t) − F (x

,t) (4.75b)

A comparison of the results of both the integrations in equation (4.73), yields

equation (4.74), which shows the contradiction resulting for the stream func-

tion ψ. The time dependence for the x

part in the right-hand side of

equation (4.75a) is missing on the left-hand side. This results from the fact

that the velocity ﬁeld given in (4.72), although mathematically clearly de-

ﬁned, cannot exist physically; the velocity ﬁeld in (4.72) does not fulﬁll the

requirements determined by the mass-conservation law for ρ = constant.

When one considers, on the other hand, the velocity ﬁeld:

=exp[x

(1 + t)],U

= −x

(1 + t)exp[x

(1 + t)],U

= 0 (4.76)

4.4 Kinematic Quantities of Flow Fields 101

for which equation (4.71) is fulﬁlled, since the following holds:

∂U

∂x

=(1+t)exp[x

(1 + t)] and

∂U

∂x

= −(1 + t)exp[x

(1 + t)] (4.77)

one obtains from the deﬁning equations for the stream function equation

(4.66):

∂ψ

∂x

=exp[x

(1 + t)] and

∂ψ

∂x

= x

(1 + t)exp[x

(1 + t)] (4.78)

the following solution for the stream function ψ:

ψ = x

exp[x

(1 + t)] + C (4.79)

If one knows the value of the stream function for x

1,0

and x

2,0

, then the

following holds:

= x

2,0

exp[x

1,0

(1 + t)] + C (4.80)

or, rewritten with ψ

ψ −ψ

= x

exp[x

(1 + t)] − x

2,0

exp[x

1,0

(1 + t)] (4.81)

The result obtained can also be computed for x

= x

1,0

= constant from

(4.66):

ψ −ψ

=(x

−x

2,0

)exp[x

1,0

(1 + t)] for x

= x

1,0

(4.82)

This expresses the distribution ψ(x

)atthelocationx

1,0

.Whenonewants

to determine the stream line in the x

−x

plane, one has to consider ψ as a

parameter in equation (4.81) and derive the relationship (x

−x

)

,forψ as

a parameter from equation (4.81). Here ψ

1,0

and x

2,0

are constants that

can be chosen freely.

4.4.3 Divergence of a Flow Field

In this section, mathematical operators will be explained that are known from

vector analysis and that can be applied to ﬂow ﬁelds. Their derivations will

be repeated but also considered in some detail with respect to their physical

meanings.

The divergence of the velocity ﬁeld U can be expressed as:

∂U

∂x

∂U

∂x

∂U

∂x

∂U

∂x

(4.83)

The above-deﬁned divergence of a velocity ﬁeld is a scalar ﬁeld which, in the

presence of a steady velocity ﬁeld, is deﬁned at each point in space and can

be computed from the velocity ﬁeld if the latter can be assumed to be known.

102 4 Basics of Fluid Kinematics

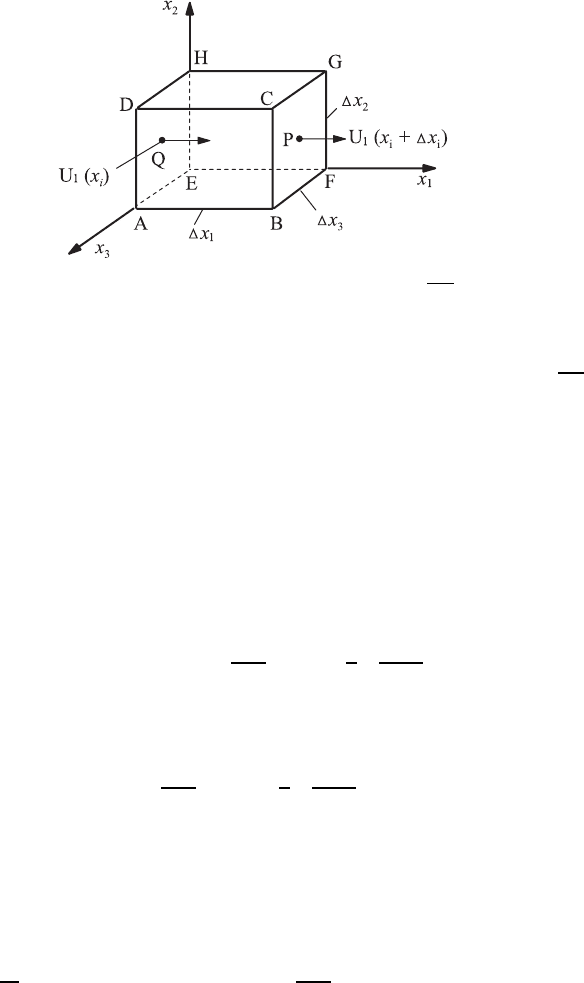
Fig. 4.9 Fluid element for explaining the physical meaning of

∂U

∂x

=divergenceof

velocity ﬁeld

When one wants to perceive the physical meaning of the operator

∂

∂x

applied to the velocity ﬁeld U

, the consideration of a single ﬂuid volume, as

indicated in Fig. 4.9, is recommended.

The edge lengths ∆x

of the considered ﬂuid element were assumed to be

very small, so that a velocity vector can be assigned to each surface such

that this vector indicates with which velocity the considered surface of a

ﬂuid element moves. Accordingly, the surface AEHD moves in the direction

with the velocity component of the velocity ﬁeld present at point Q, i.e.

with U

)=U

). In comparison, the surface BFGC moves with

the velocity component U

+ ∆x

), present at point P .Thisvelocity

component can be expressed by a Taylor series expansion as follows:

+ ∆x

)=U



∂U

∂x



∆x



∂

∂x



∆x

+ ... (4.84)

The diﬀerence velocity between the surfaces AEHD and BFGC can thus be

computed as

∆U

,∆x



∂U

∂x



∆x



∂

∂x



∆x

+ ... (4.85)

As a consequence of this velocity diﬀerence, a volume increase or a volume

decrease results, depending on the sign of the derivative of a considered ve-

locity ﬁeld. This value can be stated as follows, to a ﬁrst approximation, by

multiplication with the surface (∆x

∆x

), neglecting all the terms of second

and higher order in ∆x

(δV

)



= ∆U

)(∆x

∆x

∂U

∂x

∆x

(∆x

∆x

) (4.86)

On the basis of simultaneously existing gradients of the velocity ﬁeld in the

directions x

and x

, additional volume changes occur per unit time, which

again can be stated to a ﬁrst approximation as follows:

4.4 Kinematic Quantities of Flow Fields 103

(δV

)



∂U

∂x

∆x

(∆x

∆x

)and

(δV

)



∂U

∂x

∆x

(∆x

∆x

)

(4.87)

so that the entire volume change that can be expected in a ﬂow ﬁeld for a

ﬂuid element per unit time can be expressed as follows:

(δV )





α=1

(δV

)



∂U

∂x

(δV



) (4.88)

or can be rewritten as

∂U

∂x

δV



(δV



) (4.89)

This relationship emphasizes the physical signiﬁcance of the divergence of a

velocity ﬁeld.

The divergence of a velocity ﬁeld states how large the volume

change of a ﬂuid element is that occurs per unit time and unit volume at a

certain position in a ﬂow ﬁeld. At such locations of the ﬂow ﬁeld where the

divergence of a velocity vector is equal to zero, there is no temporal volume

change locally for a ﬂuid element moving in the velocity ﬁeld. When the

divergence in sub-domains of the velocity ﬁeld is computed to be negative, a

ﬂuid element experiences volume decreases in these domains.

When one considers the physical signiﬁcance of the divergence of a velocity

ﬁeld for a stationary volume element of a ﬂuid, inﬂows and outﬂows occur

through the surfaces of the considered volume because of the existing velocity

ﬁeld. The volume ﬂowing in per unit time can be stated as

inﬂow

= U

∆x

i = j, k (4.90)

For the volume ﬂowing out, one can compute

outﬂow



∂U

∂x

∆x



∆x

i = j, k (4.91)

The diﬀerence of inﬂows and outﬂows, considering ∆V = ∆x

,∆x

can be computed as

∆

V =

inﬂow

−

outﬂow

= −

∂U

∂x

∆V (4.92)

This relation makes it clear that the presence of a positive divergence of the

velocity ﬁeld at a point in space is equal to a “volume source”, as more “ﬂuid

volume” is ﬂowing out of the considered control volume than is ﬂowing in.

When, however, the divergence of a velocity ﬁeld is negative, a sink is present,

as then the inﬂow in the “volume” has to be larger than the outﬂow.

Equation (4.88) makes it clear that the summation for i =1− 3 is stated in a

suﬃciently comprehensible way by the subscript in ∂U

/∂x

104 4 Basics of Fluid Kinematics

4.5 Translation, Deformation and Rotation

of Fluid Elements

Analogous to considerations in solid-state mechanics, the deformations of

ﬂuid elements that occur due to existing velocity gradients are of interest

in some ﬂuid mechanics considerations. When one includes the translatory

motion and the rotation of a ﬂuid element in the ﬂuid deformations, the entire

local state of motion and deformation can be stated by four “geometrically

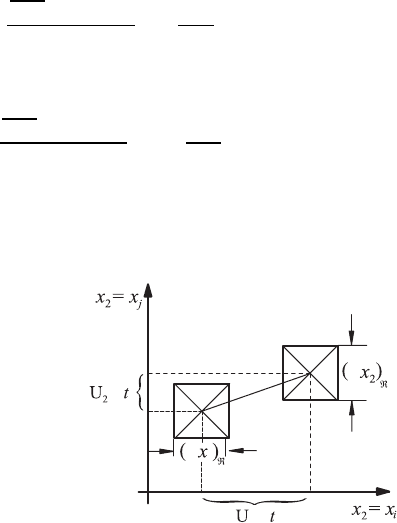
easily separable” states of motion. The pure translatory motion sketched in

Fig. 4.10 leads to a change in position of the ﬂuid element marked  to an

extent that the following holds:

d(x

)



=(U

)



dt = U

dt (4.93)

This relationship expresses that the locally existing velocity ﬁeld is responsi-

ble for the translatory motion of a ﬂuid element, i.e. ﬂuid elements move at

each moment in time with the locally existing velocity vector.

When one superimposes a ﬂuid-element rotation upon the pure translatory

motions sketched in Fig. 4.10, the image shown in Fig. 4.11 results.

In order to state or compute the rotation of a ﬂuid element, one has to

describe both the angles ∆Θ

and d∆Θ

∆Θ

⎡

⎢

⎣

tan

∂U

∂x

(∆x

)



∆t

(∆x

)



⎤

⎥

⎦

∂U

∂x

∆t (4.94)

∆Θ

⎡

⎢

⎣

tan

∂U

∂x

(∆x

)



∆t

(∆x

)



⎤

⎥

⎦

= −

∂U

∂x

∆t (4.95)

As the rotational speed of the ﬂuid element, the positive change of angle of

the diagonal of the element occurring per unit time is deﬁned as:

Fig. 4.10 Pure translatory motion; con-

siderations of the projection into the

−x

planes

∆