Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

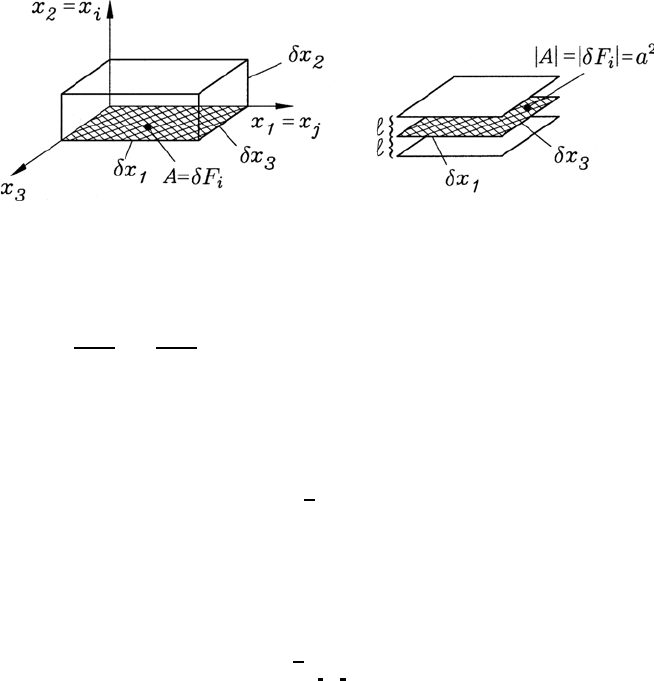
5.4 The Navier–Stokes Equations 125

Fig. 5.9 Momentum input in the x

direction caused by the molecular motion with

mean velocity u

The molecular motion is characterized by the presence of the molecular

free path lengths with ﬁnite dimensions, i.e. l = 0, and for this reason the time

averages

and u

are unequal to zero. In order to calculate the diﬀerent

contributions to the τ

terms making up the total molecular momentum

transport in ideal gases, the considerations below are recommended. For the

number of molecules moving in the direction x

and passing the plane A in

Fig. 5.9 in the time ∆t,whenδx

= δx

= a we can be write:

∆t, (5.35)

where n is equal to the number of molecules per unit volume, a

is the mag-

nitude of the area δF

of the considered volume, oriented in the i direction,

and u

is the mean velocity of the molecules in the i direction. Connected

with z

, a mass transport through δF

can be stated as follows:

(mn)





∆t, (5.36)

where m represents the mass of a molecule and thus mn = ρ can be set.

If one considers now two parallel auxiliary planes in Fig. 5.9 located at

a distances ±l above and below a main plane at δF

and if one introduces

for the derivations the mean ﬂow ﬁeld in the auxiliary planes to have the

velocity components U

+ l)andU

− l), the considerations below can

be performed. In the positive and negative i directions, the j-directional

momentum input and output can be stated as follows:

=+z

− l) momentum input over the area |δF

| = A = a

−

= − z

+ l) momentum output over the area |δF

| = A = a

(5.37)

Therefore, for the net input of momentum the sum of the molecular-

dependent input and output results:

∆i

= z

m[U

− l) − U

+ l)], (5.38)

126 5 Basic Equations of Fluid Mechanics

or, with z

inserted from (5.35):

∆i

(mn)





∆t[U

− l) − U

+ l)]. (5.39)

The net momentum input per unit area and unit time can be obtained by

Taylor series expansion of the velocity terms around x

. This can be expressed

as given below by neglecting the higher order terms:

∆i

∆t

ρu



) −

∂U

∂x

l − U

) −

∂U

∂x



, (5.40)

so that for Term II in (5.34) can be expressed as follows:

= −

ρu





∂U

∂x

= −µ

∂U

∂x

. (5.41)

Analogous to this, considerations can be carried out on τ

III

,whereforz

it can be written

∆t. (5.42)

In accordance with Term III in (5.34), a j-momentum input results, see

Fig. 5.10, which can be expressed as follows:

= z

− l)

−

= −z

+ l)

, (5.43)

∆i

= z

m[U

− l) − U

+ l)]. (5.44)

Analogous to the derivations in (5.38) to (5.41):

III

= −

(ρu



 

∂U

∂x

= −µ

∂U

∂x

. (5.45)

Fig. 5.10 Momentum input in the x

direction with molecular velocity u

and ﬂuid

velocity U

5.4 The Navier–Stokes Equations 127

For reasons of symmetry τ

= τ

,sothatu

= u

has to hold, i.e. the mean

velocity ﬁeld of the molecules is isotropic (no preferred velocity direction), so

that the total j-momentum transport can be written as:

= τ

+ τ

III

= −µ



∂U

∂x

∂U

∂x



. (5.46)

This is the total momentum input τ

for ρ = constant, i.e. when

d/dt(δV



) = 0, the thermodynamic state equation for a thermodynamically

ideal liquid is assumed to be valid. For ρ = constant, an additional term

needs to be added to τ

which is caused by the volume increase of a ﬂuid

element. For the volume increase of a ﬂuid element at point x

and time t

(see Chap. 4), one can write:

d(δV



)

=(δV



)

∂U

∂x

. (5.47)

For the corresponding surface increase the following relationship holds:

d(δF



)

(δF



)

∂U

∂x

. (5.48)

With this surface increase in time an increased momentum input results:

=+µ

∂U

∂x

. (5.49)

This term has to be added to obtain the general τ

-relationship for the total

momentum input per unit time and unit area for ideal gases. It can be stated

as follows:

= −µ



∂U

∂x

∂U

∂x



∂U

∂x

. (5.50)

If one considers this equation for τ

, the basic equations of ﬂuid mechanics

can be written as follows:

Continuity equation:

∂ρ

∂t

∂(ρU

)

∂x

=0. (5.51)

Momentum equations (j =1, 2, 3):



∂U

∂t

+ U

∂U

∂x



= −

∂P

∂x

−

∂τ

∂x

+ ρg

. (5.52)

For Newtonian ﬂuids:

= −µ



∂U

∂x

∂U

∂x



∂U

∂x

. (5.53)

128 5 Basic Equations of Fluid Mechanics

With τ

expressed by equation (5.53) there exist equations for the six un-

known terms τ

in the momentum equations. The four diﬀerential equations,

one continuity equation and three momentum equations, contain ﬁve remain-

ing unknowns P, ρ, U

, so that an incomplete system of partial diﬀerential

equations still exists. With the aid of the thermal energy equation and the

thermodynamic state equation, valid for the considered ﬂuid, it is possible to

obtain a complete system of partial diﬀerential equations that permits gen-

eral solutions for ﬂow problems, when initial and boundary conditions are

present.

For ρ = constant and µ = constant, using

∂

∂x

∂

∂x

∂

∂x



∂U

∂x



=0,

the following set of equations can be stated:

Continuity equation:

∂U

∂x

=0. (5.54)

Navier–Stokes equations (j =1, 2, 3) (momentum equations):



∂U

∂t

+ U

∂U

∂x



= −

∂P

∂x

+ µ

∂

∂x

+ ρg

This system of equations comprises four equations for the four unknowns

P , U

, U

. In principle, it can be solved for all ﬂow problems to

be investigated if suitable initial and boundary conditions are given. For

thermodynamically ideal liquids, i.e. ρ = constant, a complete system of

partial diﬀerential equations exists through the continuity equation and the

momentum equations, which can be used for solutions of ﬂow problems.

5.5 Mechanical Energy Equation

In many ﬁelds in which ﬂuid mechanics considerations are carried out, the

mechanical energy equation is employed, which can, however, be derived from

the momentum equation. For this purpose, one multiplies equation (5.52) by



∂U

∂t

+ U

∂U

∂x



= −U

∂P

∂x

− U

∂τ

∂x

+ U

ρg

. (5.55)

This equation can be rearranged to yield



∂

∂t





+ U

∂

∂x





= −

∂(PU

)

∂x

+ P

∂U

∂x

−

∂(τ

)

∂x

+ τ

∂U

∂x

+ ρg

. (5.56)

This relationship expresses how the kinetic energy of a ﬂuid element changes

at a location due to energy production and dissipation terms that occur on the

5.5 Mechanical Energy Equation 129

right-hand side of (5.56). In order to discuss the signiﬁcance of the diﬀerent

terms, the following modiﬁcation of the last term is carried out, introducing

a potential G from which the gravitational acceleration g

is derived:

= −

∂G

∂x

; ρg

= −ρ

∂G

∂x

. (5.57)

Thus, employing

∂G

∂t

=0,onecanwrite:

ρg

= −ρ



∂G

∂t

+ U

∂G

∂x



= −ρ

. (5.58)

The combined equation (5.56) and (5.58) yield for the temporal change of

the kinetic and potential energy of a ﬂuid element



+ G



= −

∂(PU

)

∂x

  

+ P

∂U

∂x

 

−

∂(τ

)

∂x

  

III

+ τ

∂U

∂x

  

, (5.59)

where the terms I–IV have the following physical signiﬁcance:

Term I: This term describes the diﬀerence between input and output of

pressure energy. This refers to the considerations of ideal gases, in

the framework of which it was shown that P =

, i.e. the pres-

sure expresses an energy per unit volume. Therefore, the following

can be said:

) = input of pressure energy per unit area

−(PU

+ ∆x

)) = output of pressure energy per unit area.

Taylor series expansion and forming the diﬀerence yields for the

energy per unit volume:

) −



(∂PU

)

∂x

+ ···



−

(∂PU

)

∂x

. (5.60)

Term II: This term requires the following considerations:

with

∂U

∂x

δV



d(δV



)

, (5.61)

the term P

∂U

∂x

δV



d(δV



)

(5.62)

130 5 Basic Equations of Fluid Mechanics

proves to be the work done during expansion, expressed per unit

volume.

Term III: When taking into consideration that τ

represents the molecular-

dependent momentum transport per unit area and unit time into

a ﬂuid element:

−

∂(τ

)

∂x

represents the diﬀerence between the molecular

input and output of the kinetic energy of the ﬂuid.

Term IV: The term τ

∂U

∂x

describes the dissipation of mechanical energy

into heat.

The above derivations show that the mechanical energy equation can

be deduced from the j momentum equation by multiplication by U

.Itis

therefore not an independent equation and hence should not be employed

along with the momentum equations for the solution of ﬂuid mechanics

problems.

A special form of the mechanical energy equation is the Bernoulli equa-

tion, which can be derived from the general form of the mechanical energy

equation:



+ G



= −

∂P

∂x

−

∂τ

∂x

. (5.63)

For τ

=0and

∂P

∂t

=0,andalsoρ = constant,



+ G



= −ρ

⎡

⎣

∂





∂t

+ U

∂





∂x

⎤

⎦

, (5.64)



+ G



=0 ;

+ G = constant. (5.65)

This form of the mechanical energy equation can be employed in many

engineering applications to solve ﬂow problems in an engineering manner.

5.6 Thermal Energy Equation

The derivations in Sect. 5.5 showed that the mechanical energy equation is

derivable from the momentum equation, so that both equations have to be

considered as not being independent of each other. From the derivations the

following form of the energy equation was obtained:







= −

∂(PU

)

∂x

+ P

∂U

∂x

−

∂(τ

)

∂x

+ τ

∂U

∂x

+ ρg

. (5.66)

5.6 Thermal Energy Equation 131

When one sets up the energy equation with the total energy balance, the

considerations stated below result, which start from the entire internal, the

kinetic and the potential energies of a ﬂuid element and consider its evolution

as a function of time:



δm





+ e + G





 

···



= δm



[...]+[...]

dδm



For the temporal change of the total energy of a ﬂuid element one obtains

with δm



= constant, i.e.

(δm



)=0:



δm





+ e + G



= δm





+ e + G



This is the total energy change with time of a ﬂuid element which has to

be considered concerning the derivation of the total energy equation.

The change in the total energy of the ﬂuid element can emanate from

the heat conduction, which yields the following inputs minus the output of

heat:

−

∂ ˙q

∂x

δV



= energy input into δV



per unit time by heat conduction

An energy input can also originate from the convective transport of

pressure energy:

−

∂

∂x

(PU

)δV



= input of pressure energy into δV



through convection

Also, the input of kinetic energy due to molecular transport into the ﬂuid

element has to be considered:

−

∂

∂x

(τ

)δV



= molecular-dependent input of kinetic energy

The following total energy balance thus results:

ρδV





+ e + G



= −

∂ ˙q

∂x

δV



−

∂(PU

)

∂x

δV



−

∂ (τ

)

∂x

δV



. (5.67)

As δV



= 0, it follows that



e +



+ G



= −

∂ ˙q

∂x

−

∂(PU

)

∂x

−

∂ (τ

)

∂x

. (5.68)

132 5 Basic Equations of Fluid Mechanics

When one deducts from this the derived mechanical parts of the energy, i.e.

by subtracting from equation (5.68) the equation for the mechanical energy,

given here once again:



+ G



= −

∂(PU

)

∂x

+ P

∂U

∂x

−

∂ (τ

)

∂x

+ τ

∂U

∂x

, (5.69)

one obtains the thermal energy equation:





= −

∂ ˙q

∂x



−P

∂U

∂x

 

III

−τ

∂U

∂x

  

. (5.70)

Term I: Temporal change of the internal energy of a ﬂuid per unit

volume.

Term II: Heat supply per unit time and unit area.

Term III: Expansion work done per unit volume and unit time.

Term IV: Irreversible transfer of mechanical energy into heat, per unit

volume and unit time.

Considering the energy equation of technical thermodynamics:



=de



+ P



− dl

diss

, (5.71)

and the sign convention usually applied in technical thermodynamics, that

the energy to be dissipated by a ﬂuid element has to be regarded as negative,

one obtains



;



= −

∂ ˙q

∂x

; P



∂U

∂x

and

diss

∂U

∂x

(5.72)

The above derivations thus lead to the form of energy equation used in

thermodynamics but through the above derivation the energy per unit time

results.

Diﬀerent forms of the thermal energy equation can be derived from equa-

tion (5.70), I is advantageous for most ﬂuid mechanics computations, to

substitute the internal energy (e) by pressure and temperature relationships,

the following relations being employed in most text books.

Generally, it can be written for thermodynamically simple ﬂuids that





∂e

∂υ



dυ +



∂e

∂T



dT =



∂e

∂υ



dυ + c

dT. (5.73)

Considering the Maxwell relationships of thermodynamics, one can be

write



∂e

∂υ



= −P + T



∂P

∂T



, (5.74)

5.6 Thermal Energy Equation 133

so that the following form of the energy equation can be given:

−P + T



∂P

∂T



∂U

∂x

+ ρc

. (5.75)

The thermal energy equation can thus also be written as:

ρc

= −

∂ ˙q

∂x

− T



∂P

∂T



∂U

∂x

− τ

∂U

∂x

. (5.76)

For an ideal gas, as

∂P

∂T

and ˙q

= −λ

∂T

∂x

ρc

= λ

∂

∂x

− P

∂U

∂x

− τ

∂U

∂x

. (5.77)

For a thermodynamically ideal liquid, as

∂U

∂x

=0andc

= c

, therefore:

ρc

= λ

∂

∂x

− τ

∂U

∂x

. (5.78)

It was shown above that the equation for the change of the total energy

can be derived by addition of the equations for the mechanical and thermal

energies:

Equation for mechanical energy:



+ G



= −

∂

∂x

(PU

)+P

∂U

∂x

−

∂

∂x

(τ

)+τ

∂U

∂x

. (5.79)

Equation for thermal energy:

= −

∂ ˙q

∂x

− P

∂U

∂x

− τ

∂U

∂x

. (5.80)

Equation for the total energy:



+ G + e



= −

∂ ˙q

∂x

−

∂

∂x

(PU

) −

∂

∂x

(τ

)

= λ

∂

∂x

−

∂

∂x

(PU

) −

∂

∂x

(τ

)

. (5.81)

From this ﬁnal relationship, the Bernoulli equation can be derived, which

is often used for ﬂuid mechanics considerations in engineering:

Ideal Liquid (ρ = constant): no heat conduction and viscous dissipation:





+ G



= −U

∂P

∂x

= −U

∂P

∂x

. (5.82)

134 5 Basic Equations of Fluid Mechanics

For a steady ﬂow:



  

∂

∂t



+ G



+ U

∂

∂x



+ G



= −U

∂P

∂x

, (5.83)

∂

∂x



+ G +



or after integration,

+ G +

= constant. (5.84)

Ideal Gas: P/ρ = RT , no heat conduction and neglecting viscous dissipation

and not considering the potential energy:



+ e



= −

∂

∂x

(PU

)=−

∂

∂x

(PU

). (5.85)

For steady-state ﬂows:

∂

∂x



+ e



= −

∂

∂x

(PU

)=−P

∂U

∂x

− U

∂P

∂x

. (5.86)

From the continuity equation, it follows for steady-state ﬂows that

∂U

∂x

= −U

∂ρ

∂x

. (5.87)

If one inserts into the considerations e = c

T , the following equations result:

∂

∂x



+ e



= ρ

∂

∂x





+ ρc

∂T

∂x

∂ρ

∂x

−

∂P

∂x

∂

∂x





∂ρ

∂x

−

∂P

∂x

− c

∂T

∂x

(5.88)

Introducing

∂T

∂x

= −

Rρ

∂ρ

∂x

Rρ

∂P

∂x

, (5.89)

∂

∂x





∂ρ

∂x





−

∂P

∂x





= −

κ − 1

∂

∂x





(5.90)

yields the Bernoulli equation in its “compressible form”:

∂

∂x



κ − 1





=0⇒

κ − 1





= constant. (5.91)