Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

5.8 Special Forms of the Basic Equations 145

Considering that





= ρ

∂

∂t





+ ρU

∂

∂x





, (5.154)

and that moreover the following conversions of terms are possible:

∂

∂t





∂P

∂t

−

∂ρ

∂t

, (5.155)

ρU

∂

∂x





= U

∂P

∂x

−

∂ρ

∂x

, (5.156)

then (5.154) can be written as:





∂P

∂t

+ U

∂P

∂x

−

Dρ

. (5.157)

From (5.154) and (5.157) one obtains





+ G



= −U

∂P

∂x

= −ρ





∂P

∂t

−

Dρ

, (5.158)

or, after conversion of some terms,





+ G



∂P

∂t

−

Dρ

. (5.159)





+ G



∂P

∂t

∂U

∂x

P. (5.160)

For stationary pressure ﬁelds

∂P

∂t

= 0, and, for ρ = constant, the Bernoulli

equation can be stated as follows:

+ G =

− x

= constant. (5.161)

The above derivations make it clear under which conditions the well-known

Bernoulli (5.161) holds.

From the above derivations, the general form of the mechanical energy

equation, by introducing dissipation into the considerations, can be written

in the following form:



+ G



∂P

∂t

+ P

∂U

∂x

∂

∂x

(τ

) − τ

∂U

∂x

. (5.162)

The left-hand side of this form of the mechanical energy equation contains

all terms of the Bernoulli equation.

146 5 Basic Equations of Fluid Mechanics

5.8.3 Crocco Equation

The Crocco equation is a special form of the momentum equation which

shows in an impressive manner how purely ﬂuid mechanics considerations

can be supplemented by thermodynamic considerations, yielding new insights

into ﬂuid ﬂows. The Crocco equation connects the vorticity of a ﬂow ﬁeld

to the entropy of the considered ﬂuid. It can be shown from this equation

that isotropic ﬂows are free of rotation and vice versa, at least under certain

conditions. So, when one recognizes a ﬂow ﬁeld to be isentropic, the simpliﬁed

rotation-free ﬂow ﬁeld considerations can be applied.

For the derivation of the Crocco equation, one starts from the Navier–

Stokes equation, as stated in (5.143) supplemented by ν = 0, i.e. one

introduces an ideal ﬂuid into the considerations, by neglecting viscous forces:

∂U

∂t

+ ∇



U · U



− U × (∇×U)=−

∇P. (5.163)

In Sect. 3.6, it was shown that:



=de



+ P



dυ



=de



+ P









. (5.164)

With e



= h



− P



/ρ



, the following relation holds:



− d







= −P









+ T



. (5.165)

Because d







= P











it holds that

−



= T



− dh



. (5.166)

This relation can also be written in ﬁeld variables as:

−

∇P = T ∇s −∇h. (5.167)

Equation (5.167) is inserted in (5.163) to yield:

∂U

∂t

+ ∇



U · U



− U × (∇×U)=T ∇s −∇h. (5.168)

5.8 Special Forms of the Basic Equations 147

For stationary adiabatic processes, the thermal energy equation can be

written in the following form:

. (5.169)

From the momentum equation, it follows further that:





= −U ∇P. (5.170)

Hence



h +



− U ∇P, (5.171)



h +



. (5.172)

Equation (5.172), inserted in (5.163) under stationary ﬂow conditions, yields

the following relationship

U × ω + T ∇s = ∇



h +



. (5.173)

If a ﬂow is considered along a ﬂow line, then ∇(h +1/2U · U) is a vector

perpendicular to the considered ﬂow line. U ×ω is also a vector and also lies

perpendicular to the ﬂow line. Hence T ∇s lies vertical to the ﬂuid motion

along a ﬂow line, and therefore it can be stated that:

+ T



h +



, (5.174)

when

h +

is constant along a ﬂow ﬁeld, then

h +

=0and

thus

+ T

=0. (5.175)

If ω

=0then ds/ dn = 0, hence rotation-free ﬂows are isentropic and vice

versa. If the ﬂow is assumed to be stationary and in the absence of viscosity,

the inertial forces turn out to be zero.

5.8.4 Further Forms of the Energy Equation

The close connection between ﬂuid mechanics and thermodynamics becomes

clear from diﬀerent forms of the energy equation, summarized in the following

table, as introduced by Bird, Steward and Lightfoot [5.1] with the notation

adapted in this book.

148 5 Basic Equations of Fluid Mechanics

Symbol Explanation Dimensions

Heat capacity at constant pressure, L

/(Tt

)

per unit mass

Heat capacity at constant volume, L

/(Tt

)

per unit mass

total

Total energy of the ﬂuid, per L

unit mass

e Internal energy, per unit mass L

g, g

External mass acceleration L/t

G Potential energy, potential of GML

h Enthalpy L

P Pressure ﬁeld M/(Lt

)

q,˙q

Heat ﬂow per unit area M/t

T Absolute temperature T

U , U

Velocity ﬁeld L/t

V Volume L

Cartesian coordinates L

β Thermal expansion coeﬃcient 1/T

ρ Fluid density ﬁeld M/L

τ, τ

Molecular momentum transport M/(Lt

)

Mass conservation (continuity equation)

Equations in vector and tensor notation Special forms

Dρ

= −ρ(∇·U )For

Dρ

=0;(∇·U )=0

Dρ

= −ρ

∂U

∂x

∂U

∂x

Equation of motion (momentum equation)

Special Equations in vector and Special forms

form tensor notation

Imposed ρ

= −∇P − [∇·τ ]+ρg For ∇·τ = 0 one obtains the

convection Euler equations

= −

∂P

∂x

−

∂τ

∂x

+ ρg

Free ρ

= −[∇·τ ] − ρβg∆T This equation

convection comprises approximations

= −

∂τ

∂x

− ρβg

∆T by Boussinesque

assumptions

5.8 Special Forms of the Basic Equations 149

Energy equations

Special form Equations in vector and tensor notation Special forms

Written

for ρ

total

= −(∇·q) − (∇·ρU ) − (∇·[τ · U ]) Exact only

total

= e+forG time

+ Gρ

total

= −

∂ ˙q

∂x

−

∂(PU

)

∂x

−

∂(τ

)

∂x

independent

D(e+

)

= −(∇·q ) − (∇·ρU )

−(∇·[τ · U ]) + ρ(U · g)

e +

D(e+

)

= −

∂ ˙q

∂x

−

∂(PU

)

∂x

−

∂(τ

)

∂x

+ ρU

= −(U ·∇P ) − (U ·[∇·τ ])

+ρ(U ·g)

= −U

∂P

∂x

− U

∂τ

∂x

+ ρU

= −(∇·q) − P (∇·U ) − (τ : ∇U )Theterm

e containing P

= −

∂ ˙q

∂x

− P

∂U

∂x

− τ

∂U

∂x

is zero for

Dρ

= −(∇·q) − (τ : ∇U )+

= −

∂ ˙q

∂x

− τ

∂U

∂x

Written ρc

= −(∇·q) − T (

∂P

∂T

)

(∇·U ) For an ideal

for −(τ : ∇U ) gas (

∂P

∂T

)

and T

ρc

= −

∂ ˙q

∂x

− T (

∂P

∂T

)

(

∂U

∂x

) − τ

∂U

∂x

Written ρc

= −(∇·q)+(

∂ ln V

∂ ln T

)

For an ideal

for −(τ : ∇U ) gas

(

∂ ln V

∂ ln T

)

and T

ρc

= −

∂ ˙q

∂x

∂ ln V

∂ ln T

)

− τ

∂U

∂x

150 5 Basic Equations of Fluid Mechanics

5.9 Transport Equation for Chemical Species

In many domains of engineering science, investigations of ﬂuids with chemical

reactions are required, which make it necessary to extend the considera-

tions carried out so far. It is necessary to state the basic equations of ﬂuid

mechanics for the diﬀerent chemical components:

• Local change of the mass per unit time of

the chemical component A

∂ρ

∂t

ρV



• Change of the mass of component A by

inﬂow and outﬂow of A

−

∂

∂x

)

δV



• Production of the chemical component A

by chemical reactions in V



δV



This yields a mass balance:

∂ρ

∂t

δV



= −

∂

∂x

[ρ

)

] δV



+ r

δV



, (5.176)

and the equation for the mass conservation for the chemical component A of

a ﬂuid is

∂ρ

∂t

∂

∂x

[ρ

)

]=r

. (5.177)

For a chemical component B, as a consequence of identical considerations,

∂ρ

∂t

∂

∂x

[ρ

)

]=r

. (5.178)

The addition of these equations yields

∂ρ

∂t

∂ (ρU

)

∂x

=0, (5.179)

i.e. the total mass conservation equation for a mixture of diﬀerent components

is equal to the continuity equation for a ﬂuid which consists of one chemical

component only. By considering Fick’s law of diﬀusion, it can be stated that

∂ρ

∂t

∂

∂x

(ρ

∂

∂x



ρD

∂ (C

/C)

∂x



+ r

. (5.180)

For ρ = constant and D

= constant, one obtains

∂ρ

∂t

  

∂U

∂x

+ U

∂ρ

∂x

= D

∂

∂x

+ r

, (5.181)

References 151

or, expressed in terms of concentration, C



∂C

∂t

+ U

∂C

∂x



= D

∂

∂x

+ R

(5.182)

with r

= AR

[5.1].

References

5.1. Bird, R.B., Stewart, W.E. and Lightfoot, E.N., Transport Phenomena, John

Wiley and Sons, New York, 1960.

5.2. Spurk, J.H., Str¨omungslehre – Einf¨uhrung in die Theorie der Str¨omungen,

Springer-Verlag, Berlin, 4. Auﬂ., 1996.

5.3. Brodkey, R.S., The Phenomena of Fluid Motions, Dover, New York, 1967.

5.4. Sherman, F.S., Viscous Flow, McGraw-Hill, Singapore, 1990.

5.5. Schlichting, H., Boundary Layer Theory, 6th edition, McGraw-Hill, New York,

1968.

Chapter 6

Hydrostatics and Aerostatics

6.1 Hydrostatics

Hydrostatics deals with the laws to which ﬂuids are subjected that do not

show motions in the coordinate system in which the considerations are car-

ried out, i.e. ﬂuids which are at rest in the coordinate system employed for

the considerations. As the relationships derived in the preceding chapter rep-

resent general laws of ﬂuid motions, they are also applicable to the cases of

ﬂuids at rest, i.e. non-ﬂowing ﬂuids. Thus, from the continuity equation,

∂ρ

∂t

∂

∂x

(ρU

) = 0 (6.1)

it can be shown that for ρ = constant and U

= f(x

) the continuity equation

is given by

∂ρ

∂t

+ U

∂ρ

∂x

  

Dρ/Dt=0

+ ρ

∂U

∂x



=0 (6.2)

This means that for U

= 0 the following simple partial diﬀerential equation

holds:

∂ρ

∂t

=0 (6.3)

whose general solution can be stated as follows:

ρ = F (x

) (6.4)

The density ρ in a ﬂuid at rest is thus only a function of the spatial coordinates

. When time variations of the density of the ﬂuid occur, these lead inevitably

to motions within the ﬂuid because of the relationship between the ﬂow and

density ﬁelds attributable to the continuity equation, i.e. because of (6.4).

153

154 6 Hydrostatics and Aerostatics

The general equations of momentum can be expressed as



∂U

∂t

+ U

∂U

∂x



= −

∂P

∂x

−

∂τ

∂x

+ ρg

(6.5)

and its special form is deduced for a ﬂuid at rest (U

=0andthe

molecular-dependent momentum transport τ

) as the following system of

partial diﬀerential equations, which represents the set of basic equations of

hydrostatics and aerostatics:

∂P

∂x

= ρg

(j =1, 2, 3) (6.6)

or, written out for all three directions j = 1, 2, 3,

∂P

∂x

= ρg

∂P

∂x

= ρg

∂P

∂x

= ρg

(6.7)

In this section, the pressure distribution in a ﬂuid, mainly deﬁned by the ﬁeld

of gravity, will be considered more closely. Restrictions are made concerning

the possible ﬂuid properties; the ﬂuid is assumed to be incompressible for

hydrostatics, i.e. ρ = constant. This condition is in general fairly well fulﬁlled

by liquids, so that the following derivations can be considered as valid for

liquids, see also refs. [6.1] to [6.8].

For the derivation of the pressure distribution in a liquid at rest, a rect-

angular Cartesian coordinate system is introduced, whose position is chosen

such that the mass acceleration {g

} given by the ﬁeld of gravity shows only

one component in the negative x

direction, i.e. the following vector holds:

} =

⎧

⎨

⎩

−g

⎫

⎬

⎭

. (6.8)

Then the diﬀerential equations (6.7), given above generally for the pressure,

can be written as follows:

∂P

∂x

=0,

∂P

∂x

= −ρg,

∂P

∂x

=0 (6.9)

From ∂P/∂x

= 0, it follows that P = f(x

)andfrom∂P/∂x

it follows that P = f(x

). Thus a comparison yields P = f(x

)andthis

shows that the pressure of a ﬂuid within a plane is constant, P (x

)=const,

when it is perpendicular to the direction of the ﬁeld of gravity. The free

surface of a ﬂuid stored in a container is a plane of constant pressure and

all planes parallel to it are also planes of constant pressure. The pressure

increases in the direction that was deﬁned by g

, i.e. in the direction of the

gravitational acceleration.

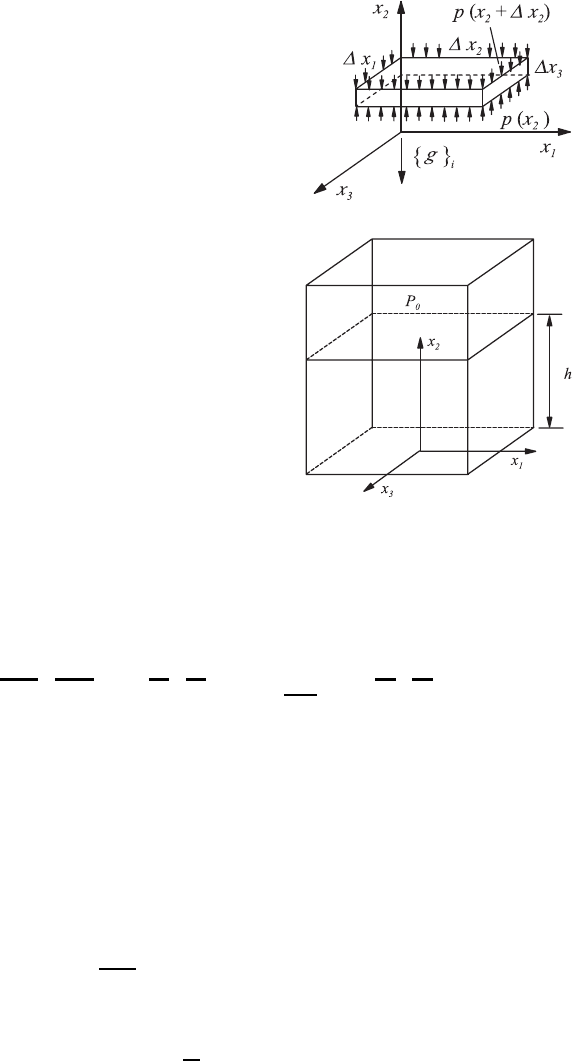
6.1 Hydrostatics 155

Fig. 6.1 Coordinate system for the derivation

of the pressure distribution in ﬂuids of constant

density

Fig. 6.2 Fluidatrestinacontainerwitha

free interface at height h

For the physical understanding of hydrostatics, it is also important to

recognize that equation (6.9) expresses that the increase in pressure in the

negative x

direction is caused by the weight of the ﬂuid element plotted in

Fig. 6.1, i.e. the following force balance holds:

−ρg

∆V

  

∆x

+ p

∆A

  

∆x

−(p +

∂p

∂x

∆x

)

∆A

  

∆x

= 0 (6.10)

Employing the above physical insights and the resultant equations, the fol-

lowing statements can be made for a liquid of constant density located in a

container (Fig. 6.2). In the case that the ﬁeld of gravity acts in the negative

direction, i.e.

=0,g

= −g, g

= 0 (6.11)

the diﬀerential equations stated in (6.9) with the solution P = f (x

)hold

for this case. Thus the partial diﬀerential ∂P/∂x

in (6.9) can be written as

a total diﬀerential and one obtains for constant density ﬂuids (ρ = constant)

= −ρg −→ P = −ρgx

+ C (6.12)

which can be rewritten as:

+ gx

= C