Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows
Подождите немного. Документ загружается.


5.2 Mass Conservation (Continuity Equation) 115
of these changes, it is important that one follows the mass δm
, i.e. one takes
x
(t) and also introduces it into consideration as known. It is assumed that
the motion of sub-parts of δm
is the same for all parts of the considered
fluid element. The fluid element is also assumed to consist at all times of the
same fluid molecules, i.e. it is assumed that the considered fluid element does
not split up during the considerations of its motion. This basically means
that the fluid belonging to a considered fluid element, at time t =0,remains
also in the fluid element at all later moments in time. This signifies that it is
not possible for two different fluid elements to take the same point in space
at an arbitrary time: x
(t) = x
L
(t)for = L.
When a fluid element is at the position x
i
at time t, i.e. x
i
=(x
(t))
i
at
time t, then the substantial thermodynamic property, or any fluid mechanic
property, α
(t) is equal to the field quantity α at the point x
i
at time t:
α
(t)=α(x
i
,t)when(x
(t))
i
= x
i
at time t. (5.1)
For the temporal change of a quantity α
(t) (see also Chaps. 2 and 3), one
can write:
dα
dt
=
∂α
∂t
+
∂α
∂x
i
dx
i
dt
. (5.2)
With (dx
i
/dt)
=(U
i
)
= U
i
:
dα
dt
=
Dα
Dt
=
∂α
∂t
+ U
i
∂α
∂x
i
. (5.3)
The operator Dt = ∂/∂t+ U
i
∂/∂x
i
applied to the field quantity α(x
i
,t)isof-
ten defined as the substantial derivatve and will be applied in the subsequent
derivations. The significance of individual terms are:
∂/∂t =(∂/∂t)
x
i
= change with time at a fixed location,
partial differentiation with respect to time
d/dt = total change with time (for a fluid element),
total differentiation with respect to time
e.g. for a fluid when α
= ρ
= constant, i.e. the density is constant, then:
dρ
dt
=
Dρ
Dt
=0 or
∂ρ
∂t
= −U
i
∂ρ
∂x
i
. (5.4)
When at a certain point in space ∂/∂t(α)
x
i
= 0 indicates stationary condi-
tions, the field property α(x
i
,t) is stationary and thus has no time depen-
dence. On the other hand, when d(α
)/dt =Dα/Dt =0,thenα
(t)=
α(x
i
,t) = constant, i.e. the field variable is independent of space and time.
5.2 Mass Conservation (Continuity Equation)
For fluid mechanics considerations, a “closed fluid system” can always be
found, i.e. a system whose total mass M = constant. This is easily seen
for a fluid mass, which is stored in a container. For all other fluid flow
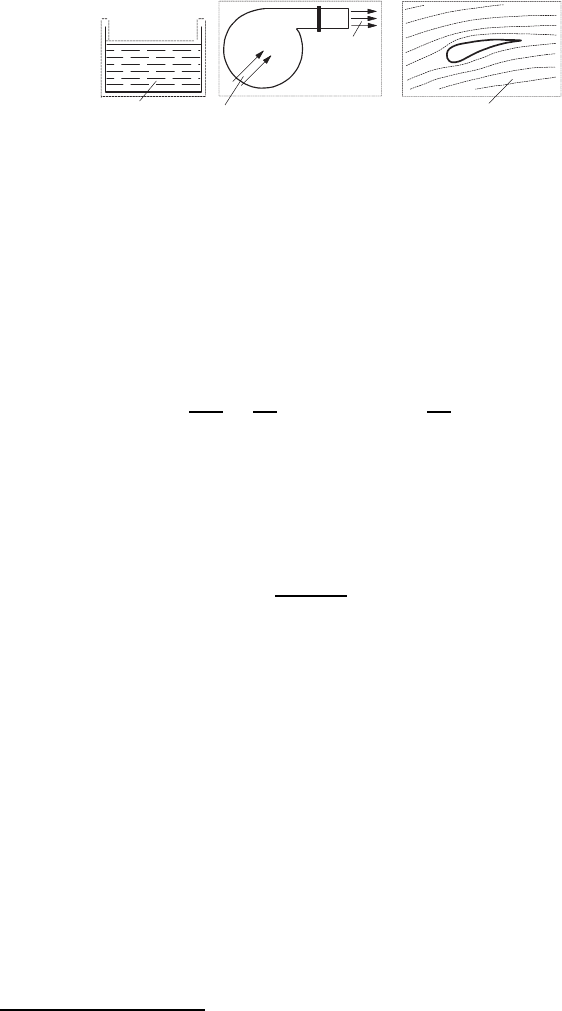
116 5 Basic Equations of Fluid Mechanics
D
M
= const
M
= const
M
= const
m
ein
.
m
aus
.
Aquarium with
constant mass
of water
Blower with air
inlet and outlet
Flow around
an aeroplane wing
Fig. 5.2 Different fluid flow cases within control volumes for which M = constant
can be set
considerations, as shown in Fig. 5.2, control volumes can always be defined
within which the system’s total mass can be stated as constant. If necessary
these control volumes can comprise the whole earth to reach M = constant.
When one subdivides the fluid mass M within the considered system into
fluid elements with sub-masses δm
, then for the temporal change of the
total mass one obtains:
0=
dM
dt
=
d
dt
(δm
)=
d
dt
(δm
). (5.5)
This equation expresses that the total mass conservation in the control
volume of the fluid system is preserved when each individual fluid ele-
ment conserves its mass δm
. With this the balance equation for the mass
conservation can be stated as follows, in Lagrange notation:
d(δm
)
dt
=0. (5.6a)
The basic molecular structure of matter and thermal motion connected with
it indicates that to fulfill the above relationship absolutely, it is necessary
that δm
→ 0 is not taken into consideration. The derivations in this book
therefore require that all the chosen δm
are considered as finite but nev-
ertheless as very small. In Fig. 5.3 a fluid element with position coordinates
(x
i
)
is shown.
1
The determination of the required size of δm
needs considerations that
are given in Chap. 3, where it is shown what dimensions a volume of an ideal
gas has to have in order to define “sufficiently clearly”, e.g. the density of the
gas within the volume. The considerations carried out there would have to be
repeated here in order to ensure δm
≈ constant, in spite of the molecular
structure of the fluid. With the choice of δm
= constant, the conditions are
set to carry out continuum mechanics considerations for the motion of fluids,
although the fluids show a molecular structure.
1
See also the considerations in Sect. 3.2.
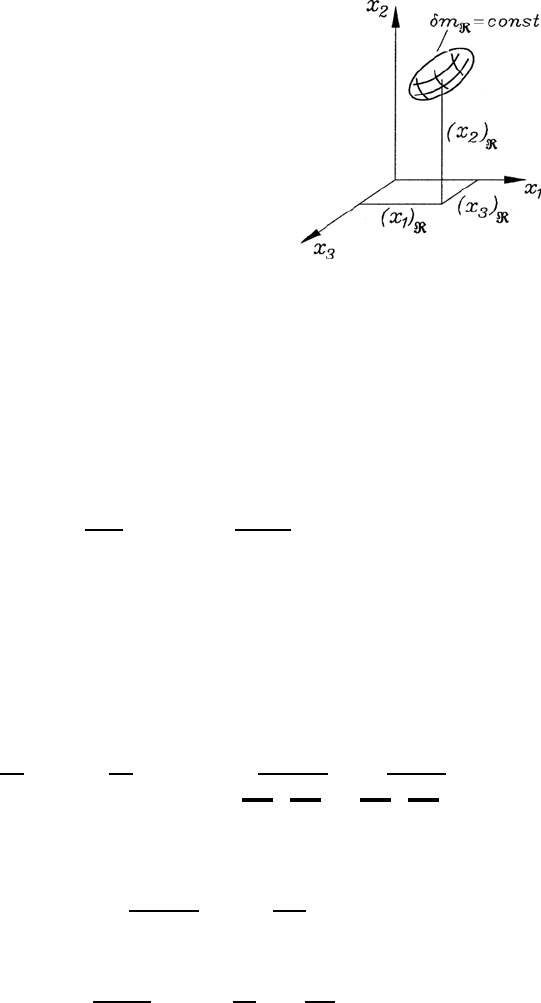
5.2 Mass Conservation (Continuity Equation) 117
Fig. 5.3 δm
= constant, condition for the mass
of a fluid element treated at (x
i
)
= x
i
It is often claimed that molecular motions are not considered when con-
tinuum assumptions are taken into fluid mechanics applications. Strictly, this
means that the properties of the molecules, especially their transport prop-
erties, can only be introduced into continuum fluid mechanics considerations
in an integral form.
Because of the above explanations, the mass conservation can be stated in
Lagrange form as follows:
dM
dt
=0 and
dδm
dt
=0. (5.6b)
The above considerations confirm that it is very simple to formulate the
mass-conservation law in Lagrange variables. Working practically with the
law of mass conservation, however, requires its representation in field quan-
tities, i.e. the Lagrange form of the mass-conservation law has to be brought
into its corresponding Euler form.
Transformed into Euler variables (i.e. into field quantities), one obtains
from (5.6a) for the mass conservation:
0=
d
dt
(δm
)=
d
dt
(ρ
δV
)=ρ
d(δV
)
dt
I
+ δV
d(ρ
)
dt
II
. (5.7)
For Term I in (5.7), using ρ
= ρ and x
(t)
i
= x
i
at time t, yields
according to (4.89):
ρ
d(δV
)
dt
= ρδV
∂U
i
∂x
i
. (5.8)
For Term II one obtains:
δV
d(ρ
)
dt
= δV
∂ρ
∂t
+ U
i
∂ρ
∂x
i
. (5.9)
With the above derivations, the substantial derivative of the corresponding
field quantity d (ρ
) /dt could be applied for ρ, i.e. Dρ/Dt, in order to achieve

118 5 Basic Equations of Fluid Mechanics
the transformation of the substantial quantity ρ
(t) to the field quantity
ρ(x
i
,t).Thesameprocedureisnotpossiblewith d(δV
) /dt since there are
no volume fields, i.e. a point has no volume. From Sect. 4.4.3, (4.89), it is
known that the temporal change of a fluid element is equal to the divergence
of the velocity field, however:
ρ
d(δV
)
dt
= δV
∂U
i
∂x
i
. (5.10)
When one inserts (5.8) and (5.9) into (5.7) one obtains:
δV
∂ρ
∂t
+ ρ
∂U
i
∂x
i
+ U
i
∂ρ
∂x
i
=0. (5.11)
As δV
= 0, it follows for the continuity equation in field variables and in
the most general form
∂ρ
∂t
+ ρ
∂U
i
∂x
i
+ U
i
∂ρ
∂x
i
=
∂ρ
∂t
+
∂(ρU
i
)
∂x
i
=0. (5.12)
The equation can also be written as follows:
∂ρ
∂t
+ U
i
∂ρ
∂x
i
+ ρ
∂U
i
∂x
i
=
Dρ
Dt
+ ρ
∂U
i
∂x
i
=0. (5.13)
The right hand side of the continuity equation is not very useful for the
solution of flow problems. However, it is very well suited for presentation of
the basic equations of fluid mechanics in different ways, in order to bring
out special physical facts. As an example, the special form of the continuity
equation for ρ
= constant, i.e. Dρ/Dt = 0, from (5.13) results:
∂U
i
∂x
i
=0. (5.14)
i.e. the divergence of the velocity field is zero for fields of constant fluid
density. Since the divergence of the velocity field is zero, the change in volume
is also zero from (5.10), this can also be obtained from equations (3.90) and
(3.93):
1
ρ
Dρ
Dt
=
1
ρ
∂ρ
∂T
P
−β
DT
Dt
+
1
ρ
∂ρ
∂P
T
+α
DP
Dt
= −
∂U
i
∂x
i
. (5.15)
This relationship expresses for an ideal liquid, ideal in the thermodynamic
sense, ρ = constant, i.e. if the fluid density is constant, that the fluid has to
be thermodynamically incompressible.
1
ρ
Dρ
Dt
= −
∂U
i
∂x
i
=0=α
DP
Dt
− β
DT
Dt
with α =0 and β =0, (5.16)

5.3 Newton’s Second Law (Momentum Equation) 119
where α and β are:
α = −
1
v
∂v
∂P
T
=
1
ρ
∂ρ
∂P
T
= isothermal compressibility
coefficient,
β =
1
v
∂v
∂T
P
= −
1
ρ
∂ρ
∂T
P
= thermal expansion coefficient.
Thus the continuity equation holds in one of the following two forms:
∂ρ
∂t
+
∂(ρU
i
)
∂x
i
= 0 (compressible flows), (5.17)
∂U
i
∂x
i
= 0 (incompressible flows). (5.18)
For further details of these derivations, see refs. [5.1] to [5.5].
5.3 Newton’s Second Law (Momentum Equation)
The derivations of the momentum equations of fluid mechanics are usually
given for the three coordinate directions j =1,2,3.TheyexpressNew-
ton’s second law and are easiest formulated in their Lagrange forms. For a
fluid element, it is stated that the time derivative of the momentum in the
j direction is equal to the sum of the external forces acting in this direction
on the fluid element, plus the molecular-dependent input of momentum per
unit time. The forces can be stated as mass forces (δM
j
)
caused by grav-
itation forces and electromagnetic forces
2
, as well as surface forces caused
by pressure, (δO
j
)
. After the addition of a temporal change of momentum
introduced by the molecular movement input, the equation of motion can be
formulated as follows:
d(δJ
j
)
dt
=
(δM
j
)
mass forces
+
(δO
j
)
surface forces
+
d
dt
(δJ
M
)
j
molecular-dependent
momentum input
. (5.19)
Here, as shown in Fig. 5.4, (δJ
j
)
= δm
(U
j
)
.
Fluid elements act like rigid bodies. They do not change their state of
motion, i.e. their momentum, if no mass or surfaces forces act on the fluid
elements and no molecular-dependent momentum input is present. However,
when forces are present, or when molecular momentum input occurs, a con-
sidered fluid element changes its momentum in accordance with (5.19). This
equation represents the Lagrange form of the equations of momentum (j =1,
2, 3) of fluid mechanics.
2
The latter are not taken into consideration in the following.
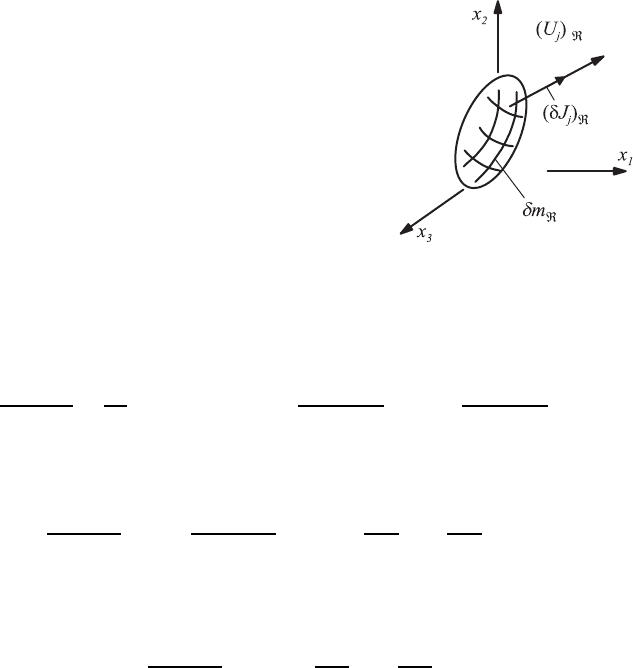
120 5 Basic Equations of Fluid Mechanics
Fig. 5.4 The derivation of momentum equations
are based on force considerations for a fluid element
In order to derive the Euler form of the equation of momentum, it is
necessary to express each of the terms contained in (5.19) in field quantities.
The left-hand side of (5.19) can be written as:
d(δJ
j
)
dt
=
d
dt
[δm
(U
j
)
]=δm
d((U
j
)
)
dt
+(U
j
)
d((δm)
)
dt
. (5.20)
Because of the mass conservation for a fluid element expressed in (5.6a), the
last term in (5.20) is equal to zero and hence one obtains:
d(δJ
j
)
dt
= δm
d((U
j
)
)
dt
= δm
∂U
j
∂t
+ U
i
∂U
j
∂x
i
. (5.21)
This relationship can be written as follows: δm
= ρ
δV
= ρδV
applying
ρ
= ρ when (x
(t))
i
= x
i
at time t:
d(δJ
j
)
dt
= ρδV
∂U
j
∂t
+ U
i
∂U
j
∂x
i
. (5.22)
In accordance with the above derivations, it is possible to state the left-
hand side of the equation of momentum (5.19) in field quantities as shown in
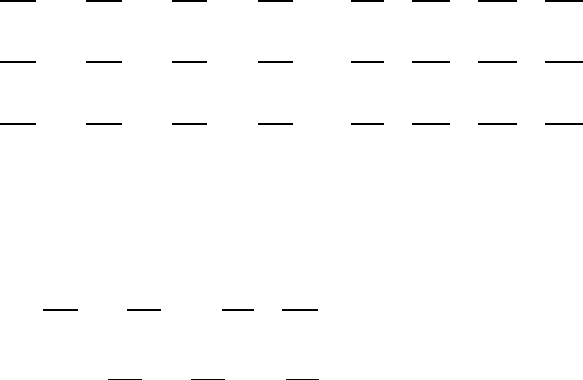
(5.22). For the right-hand side the considerations below can be carried out.
The mass forces:
(δM
j
)
= mass forces acting on a fluid element
acting on a fluid element can be expressed by means of the accelera-
tion {g
j
} = {g
1
,g
2
,g
3
} acting per unit mass (Fig. 5.5). The mass force
acting on a fluid element in the j direction can therefore be stated as
follows:
(δM
j
)
=(δm)
g
j
= ρδV
g
j
. (5.23)
Even when only gravitational acceleration is present, depending on the
orientation of the coordinate system, several components of g
j
may exist and
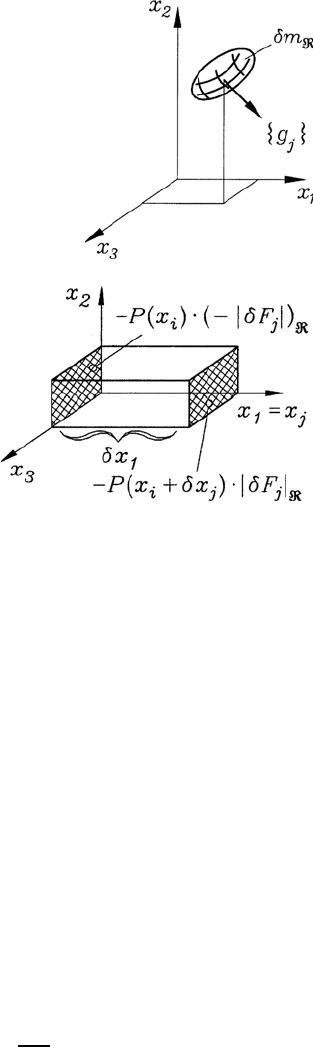
5.3 Newton’s Second Law (Momentum Equation) 121
Fig. 5.5 Mass forces acting on a fluid element in
the directions j =1, 2, 3
Fig. 5.6 Considerations concerning sur-
face force on a fluid element in the
directions j =1, 2, 3
have to be taken into account:
(δO
j
)
= surface forces on a fluid element.
Fluids, as they are treated in this book, i.e. liquids (e.g. water) and gases (e.g.
air), are characterized by the way they apply surface forces on a fluid element
(Fig. 5.6). The only surface forces that can exist are those imposed by the
molecular pressure. The pressure force acting on a fluid element is calculated
as the difference in the forces acting on the areas that stand vertically on the
considered axes j =1, 2, 3. For the pressure force, we can write:
dK
P
= −P dF .
The surface force resulting for the motion of the fluid element in the j
direction is the sum of the forces acting on the j planes of the element:
(δO
j
)
= −P (x
j
)(−|δF
j
|)
− P (x
j
+ δx
j
)(|δF
j
|)
. (5.24a)
If one applies a Taylor series expansion for P (x
i
+ δx
j
), one obtains:
(δO
j
)
=+P (x
j
)(|δF
j
|)
− [P (x
j
)+
∂P
∂x
j
δx
j
+ ···](|δF
j
|)
. (5.24b)
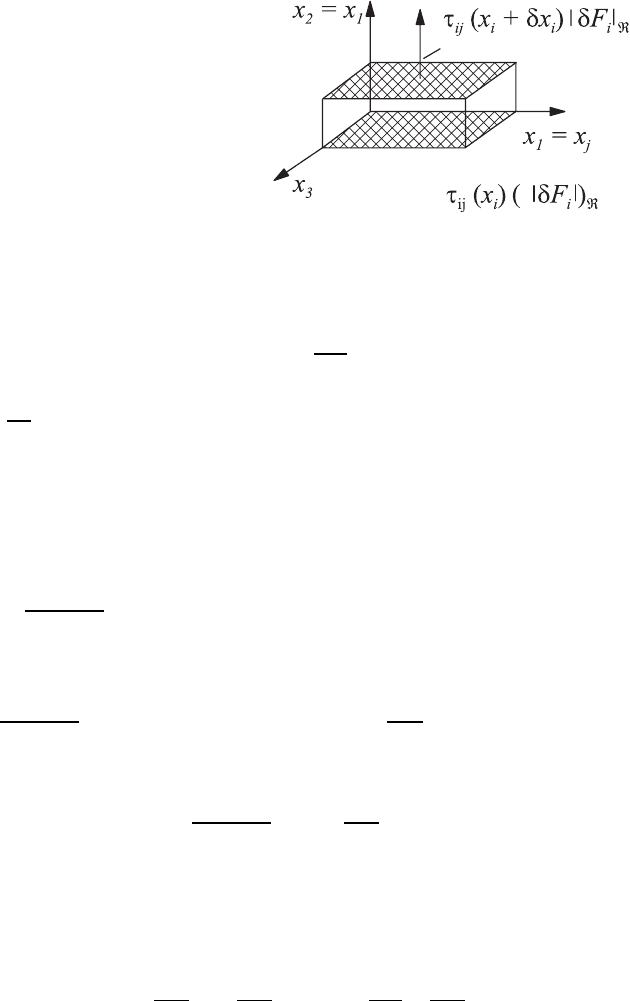
122 5 Basic Equations of Fluid Mechanics
Fig. 5.7 Considerations on the
molecular-dependent momentum
input in the j =1, 2, 3 directions
−
−
−
From this equation, one obtains for the surface force on a fluid element,
neglecting all second and higher order terms of differentiations (Fig. 5.6),
(δO
j
)
= −
∂P
∂x
j
δV
. (5.25)
d
dt
(δJ
M
)
j
=
molecular-dependent momentum input per unit time
into a fluid element.
When one defines the momentum j transported by molecules in the direc-
tion i per unit time and unit area as τ
ij
, the input influencing the momentum
j of a fluid element is calculated as an input at the position x
i
and as an
output at the position (x
i
+ ∆x
i
), e.g. see Fig. 5.7:
d(δJ
M
)
j
dt
j
= −τ
ij
(x
i
)(−|δF
j
|)
− τ
ij
(x
i
+ ∆x
i
)(|δF
i
|)
. (5.26a)
By a Taylor series expansion one obtains for the term τ
ij
(x
i
+ δx
i
)
d(δJ
M
)
j
dt
=+τ
ij
(x
i
)(|δF
i
|)
− [τ
ij
(x
i
)+
∂τ
ij
∂x
i
δx
i
···](δF
i
)
. (5.26b)
This results in:
d(δJ
M
)
j
dt
= −
∂τ
ij
∂x
i
δV
. (5.27)
When one inserts all these derived relationships (5.22), (5.23), (5.25) and
(5.27) into (5.19) and after division by δV
, the equation of momentum of
fluid mechanics in the j direction results, i.e. for j =1, 2, 3, three equations
can be given:
ρ
∂U
j
∂t
+ U
i
∂U
j
∂x
i
= ρg
j
−
∂P
∂x
j
−
∂τ
ij
∂x
i
. (5.28)
As in this equation the volume of the fluid element δV
, appearing in all
terms, was eliminated, the equations of momentum are given by (5.28) per
5.4 The Navier–Stokes Equations 123
unit volume. From the general equation (5.28), the momentum equations in
the three coordinate directions result:
ρ
∂U
1
∂t
+ U
1
∂U
1
∂x
1
+ U
2
∂U
1
∂x
2
+ U
3
∂U
1
∂x
3
= −
∂P
∂x
1
−
∂τ
11
∂x
1
−
∂τ
21
∂x
2
−
∂τ
31
∂x
3
+ ρg
1
ρ
∂U
2
∂t
+ U
1
∂U
2
∂x
1
+ U
2
∂U
2
∂x
2
+ U
3
∂U
2
∂x
3
= −
∂P
∂x
2
−
∂τ
12
∂x
1
−
∂τ
22
∂x
2
−
∂τ
32
∂x
3
+ ρg
2
ρ
∂U
3
∂t
+ U
1
∂U
3
∂x
1
+ U
2
∂U
3
∂x
2
+ U
3
∂U
3
∂x
3
= −
∂P
∂x
3
−
∂τ
13
∂x
1
−
∂τ
23
∂x
2
−
∂τ
33
∂x
3
+ ρg
3
(5.29)
For fluids in general, τ
ij
= 0, but for ideal fluids, i.e. ideal in terms of
fluid mechanics, the molecular momentum transport turns out to be τ
ij
=0.
Hence the following forms of the momentum equations can be stated:
ρ
∂U
j
∂t
+ U
i
∂U
j
∂x
i
= −
∂P
∂x
j
−
∂τ
ij
∂x
i
+ ρg
j
(viscous fluids), (5.30)
ρ
∂U
j
∂t
+ U
i
∂U
j
∂x
i
= −
∂P
∂x
j
+ ρg
j
(ideal fluids). (5.31)
For further details of these derivations see refs. [5.1] to [5.5].
5.4 The Navier–Stokes Equations
In equation (5.30), the molecular-dependent momentum input τ
ij
was intro-
duced as an input as per unit surface area and unit time. It is an unknown
term, i.e. it was introduced formally into the derivations without any details
being considered as to how it can be formulated for various fluids. When one
takes into consideration the symmetry of the term τ
ij
, i.e. |τ
ij
| = |τ
ji
|,one
finds that there are the following unknowns in the above equations:
U
1
,U
2
,U
3
,P,τ
11
,τ
12
,τ
13
,τ
22
,τ
23
,τ
33
= 10 unknowns.
For these unknowns there are only four partial differential equations avail-
able to provide solutions to fluid flow problems, the continuity equation and
three equations of momentum, i.e. an incomplete system of equations exists
that does not permit the solution of flow problems. It is therefore neces-
sary to state additional equations, i.e. to express the unknown terms τ
ij
in
a physically well-founded manner, as functions of ∂U
j
/∂x
i
.Thisisdonebe-
low for ideal gases, as their properties are usually well known to engineering
students, from considerations in physics. From the derivations given below,
relationships for τ
ij
= f (∂U
j
/∂x
i
) result, that are valid also for non-ideal
gases, and in fact for a whole class of fluids whose molecular momentum
transport properties can be classified as “Newtonian”. Thus the derived
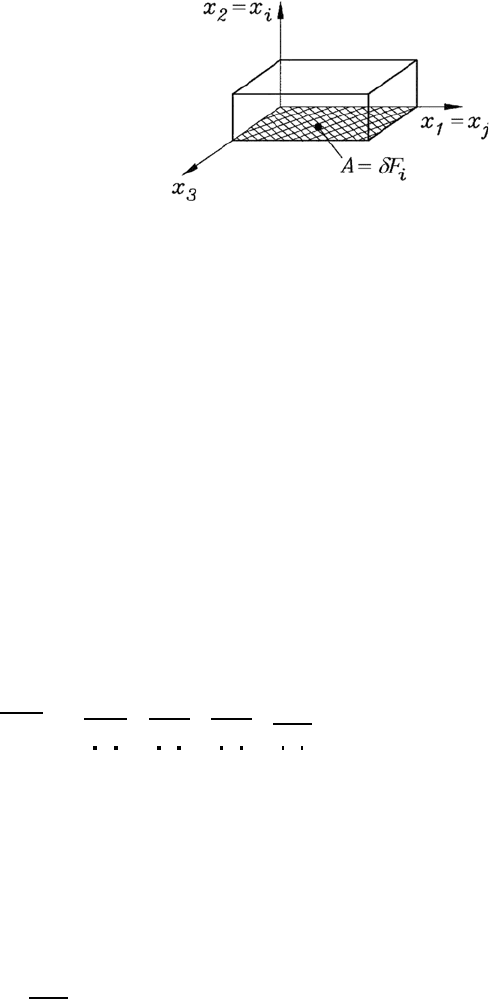
124 5 Basic Equations of Fluid Mechanics
Fig. 5.8 Momentum input due to flow
through the plane δF
i
relationships for τ
ij
are valid far beyond ideal gases and represent in this
book the basic equations to describe the molecular-dependent momentum
transport in Newtonian fluids.
If one considers a fluid element, as shown in Fig. 5.8, with side walls par-
allel to the planes of a Cartesian coordinate system, one can see that the j
momentum transported in the direction i by a velocity field U
i
can be stated
as follows:
˙
I
ij
= ρ
ˆ
U
i
ˆ
U
j
δF
i
. (5.32)
Assuming that the instantaneous velocity components are composed of the
velocity components of the fluid flow U
i
and the molecular velocity component
u
i
,onecanwrite:
ρ
ˆ
U
i
ˆ
U
j
= ρ(U
i
+ u
i
)(U
j
+ u
j
)
= ρ(U
i
U
j
+ u
i
U
j
+ u
j
U
i
+ u
i
u
j
)
. (5.33)
By time averaging, one obtains for the time-averaged total momentum
change of the fluid element:
ρ
ˆ
U
i
ˆ
U
j
= ρ[U
i
U
j
I
+ u
i
U
j
II
+ u
j
U
i
III
+ u
i
u
j
IV
]. (5.34)
The total momentum input consists of four terms that can be interpreted
physically as follows:
Term I: j Momentum input in the i direction due to the velocity field U
i
of the fluid.
Term I I: j Momentum input in the i direction due to the molecular motion
in the i direction, i.e. due to u
i
.
Term III: j Momentum input in the i direction due to the molecular motion
u
j
in the j direction.
Term IV: For i = j the
u
i
u
j
= 0, as the molecular motion in the three
coordinate directions are not correlated. For i = j the molecular
caused pressure treated in Chap. 3 results.
