Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

4.3 Motion of Fluid Elements 85

dα



∂α

∂t

dt +

∂α

∂x

dt +

∂α

∂x

dt +

∂α

∂x

dt (4.3)

Hence the total time derivative of α



(t) can be expressed as follows, if x



= x

at time t:

dα



∂α

∂t

+ U

∂α

∂x

Dα

(4.4)

where (Dα/Dt) is the substantial derivative of the ﬁeld quantity α(x

,t) with

respect to time and the operator:

∂

∂t

+ U

∂

∂x

(4.5)

indicates how the substantial derivative of a ﬁeld quantity is to be calculated.

The operator D/Dt may only be applied to ﬁeld quantities. If one applies

D/Dt to the velocity ﬁeld U

,t), the substantial acceleration results, i.e.

the local acceleration which a ﬂuid element experiences in a ﬂow ﬁeld at a

point x

at time t where U

,t) exists:

∂U

∂t

+ U

∂U

∂x

(4.6)

For further details about this subject, see refs. 4.1 to 4.3. The substantial

derivative of the velocity plays an important role in deriving the momentum

equation of ﬂuid mechanics in Euler variables. In the acceleration term in

Euler quantities, as shown by the subscript i in (4.6), four partial derivatives

occur per momentum direction j =1, 2, 3, namely one time derivative and

three derivatives with respect to the space coordinates x

and x

. Hence

the spatial derivatives (∂U

/∂x

), multiplied by U

occur as three terms in

each of the three momentum equations representing the substantial accel-

eration. These nonlinear terms lead to mathematical diﬃculties when ﬂow

problems are to be solved. They prevent the application of the superposi-

tion principle of solutions and result in solution bifurcations, i.e. in multiple

solutions for equal initial and boundary conditions, and also in correlated ve-

locity ﬂuctuations, e.g. in turbulent ﬂows. The treatment of these nonlinear

terms is given good attention in several parts of this book. It is important

that the signiﬁcance of the non-linear terms is understood in detail as part

of the acceleration term of ﬂuid elements. It is important to realize that not

only the temporal changes of the velocity ﬁeld lead to accelerations of ﬂuid

elements, but also the motion of a ﬂuid element in a non-uniform velocity

ﬁeld.

4.3 Motion of Fluid Elements

Flow kinematics is a vast ﬁeld and a comprehensive treatment is beyond

the scope of this book, which is meant to give only an introduction into

various sub-domains of ﬂuid mechanics, including ﬂuid kinematics. To such

86 4 Basics of Fluid Kinematics

an introduction belongs the treatment of path lines of ﬂuid particles, i.e. the

computation of space curves along which marked ﬂuid elements move in a

ﬂuid. Further, the computation of streak lines will be treated, i.e. the “marked

path”. This is the line a tracer mark, in a ﬂuid when it is added at a ﬁxed

point in the ﬂow. The computation of both path lines and of streak lines is

of importance for the entire ﬁeld of experimental ﬂuid mechanics, where it is

often tried to gain an insight into a particular ﬂow by observations, or also

by quantitative measurements, of the temporal changes of positions of “ﬂow

markers”. The basics for the evaluation of such measurements are stated in

the following chapter.

4.3.1 Path Lines of Fluid Elements

If one subdivides, at time t = 0, the entire domain of a ﬂow ﬁeld, that is

of interest for investigating, into deﬁned ﬂuid elements and if one deﬁnes

the space coordinates of the mass centers of gravity of each element in a

coordinate system at time t = 0, one achieves a marked ﬂuid domain such

that the position vector  can be deﬁned as follows:

}

,0

= {x

(t =0)}



(4.7)

Hence {x

}



at t = 0 is assigned to each marked ﬂuid particle. Each of the

moving ﬂuid particles, deﬁned by the subdivision of the ﬂuid in space, and

moving for −∞ <t<+∞ is deﬁned as a ﬂuid element, that keeps its identity

0 ≤ t<∞ i.e forever.

When kinematic considerations for each marked ﬂuid element are carried

out, only the motions of the individual ﬂuid elements are of interest. These

considerations result for each ﬂuid element in a separate consideration and

result for each marked element in a characteristic path line. The computation

of these path lines will be explained in the following. In all kinematic consid-

erations it can be assumed that the ﬂow ﬁeld determining the ﬂuid element

motionsisknown.

As the velocity of a ﬂuid element is dependent only on time, it follows from

d{x

}



/dt = {U

}



, that the path line of a ﬂuid element  can be calculated

as follows:

(t)}



= {x

}

,0



)}





(4.8)

The position vector {x

(t)}



, deﬁned in this way for each instant in time t,

contains as a parameter the position vector of the particle deﬁned at time

t = 0, i.e. , i.e. {x

}

,0

.Theidentity{U

}



= {U

} can be introduced into

the considerations, i.e. at a certain moment in time t, the space change of a

marked ﬂuid element can be expressed as:

d{x

}



= {U

}



= {U

} (4.9)

4.3 Motion of Fluid Elements 87

The equals sign between the substantial velocity {U

}



and {U

},existing

for a moment in time t, indicates that the identity {x

}



= {x

} which

exists at time t justiﬁes equating the substantial velocity {U

}



with the ﬁeld

velocity {U

}. For the time derivative of the components {x

}



of the particle

motion one can write:

d{x

}



= {U

} or

d(x

)



= U

(4.10)

These diﬀerential equations have to be solved, for i =1,2,3,inorderto

determine the path lines of ﬂuid elements. The diﬀerential quotient in (4.10)

states that, as a solution of the above diﬀerential equations, the path line of

that ﬂuid element  is obtained whose position was deﬁned at the moment

in time t =0with{x

}

,0

The general way of proceeding when deﬁning path lines will be explained

and made clear by the example given below. The components of the ﬂow

velocity ﬁeld will be given as follows:

= x

(1 + t),U

= −x

and U

= −x

t (4.11)

This ﬂow case was also treated by Currie in ref. [4.4]. If one inserts these

deﬁnitions of the components of the velocity ﬁeld in the above diﬀerential

equations for the path lines of a ﬂuid element, one obtains

d(x

)



= x

(1 + t)

d(x

)



= −x

(4.12)

d(x

)



= −x

This set of diﬀerential equations can be solved and results in the following

solutions holding for the path lines of all ﬂuid elements:

(t))



= C

exp



t +



(t))



= C

exp[−t] (4.13)

(t))



= C

exp



−



If one now considers a ﬂuid element of interest which had the position coor-

dinates (1, 1, 1) at time t = 0, then from the initial conditions for each of the

equations in (4.3), the introduced integration constants C

result. They can

be deduced to be

= C

= 1 (4.14)

i.e. for the case considered here all integration constants are equal. Of course,

other integration constants would have resulted from the choice of other

marked ﬂuid elements.

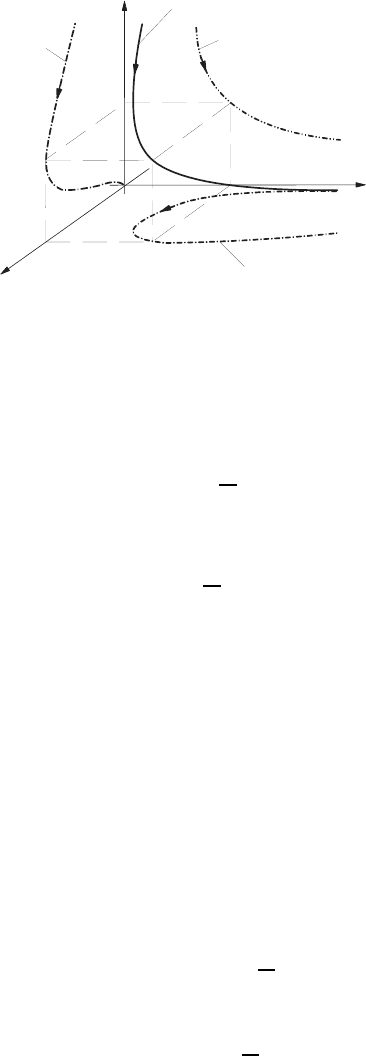
88 4 Basics of Fluid Kinematics

-x

plane

Projection into

-x

plane

-x

plane

(1,1,1)

Path line

Fig. 4.2 Spatial path line of the considered ﬂuid element and projections into planes

of coordinate system

For the path lines of the selected ﬂuid element, the introduction of C

into

(4.13) yields

(t)



=exp



t +



(t)



=exp



− t



(4.15)

(t)



=exp



−



This path line is presented in space in Fig. 4.2.

As said above, if one selects a particle whose position at time t =0showed

diﬀerent position coordinates, the integration constants C

and C

change

accordingly and a diﬀerent path line results. Thus the path line is an “indi-

vidual” property of a ﬂuid element. It is determined by the ﬂow ﬁeld and the

position of the ﬂuid element at time t =0.

The general solution for the position coordinates (x

)

,0

, which a ﬂuid

element takes at time t = 0, is obtained when one inserts these coordinates

in the general solutions for the path line coordinates for the determination

of the integration constants C

(α =1,2,3).Thisresultsin

=(x

)

,0

(4.16)

and thus in the general solutions for the path line coordinates:

(t))



=(x

)

,0

exp



t +



(t))



=(x

)

,0

exp[−t] (4.17)

(t))



=(x

)

,0

exp



−



4.3 Motion of Fluid Elements 89

These coordinates yield the space curves, with the time t as parameter, which

represent the path lines of ﬂuid elements. Each ﬂuid element has its own path

line.

For further explanation, the following two-dimensional velocity ﬁeld is also

considered

= x

(1 + 2t)andU

=0. (4.18)

With these data, the following law of diﬀerential equations for the coordinates

of the path lines of ﬂuid elements can be formulated:

d(x

)



= x

d(x

)



= x

(1 + 2t),

d(x

)



= 0 (4.19)

The solution of the third diﬀerential equation results in a constant that states

in which plane the two-dimensional ﬂow considerations need to be carried out.

For the path line coordinates x

(t)andx

(t) it is computed from (4.10)

)



= C

exp[t], (x

)



= C

exp[t + t

], (x

)



= C

(4.20)

When one computes the path line of the ﬂuid element which at time t =0

took the coordinates (1,1,0), the result is

)



=exp[t], (x

)



=exp[t(t +1)], (x

)



= 0 (4.21)

When one resolves the equation obtained for (x

)



with respect to time, the

following can be deduced:

t =ln(x

)



(4.22)

Inserting this in the solution for (x

)



for two-dimensional path lines in the

plane x

−x

−, the following functional relation between (x

)



and (x

)



results:

)



=(x

)

(1+ln(x

)



)



(4.23)

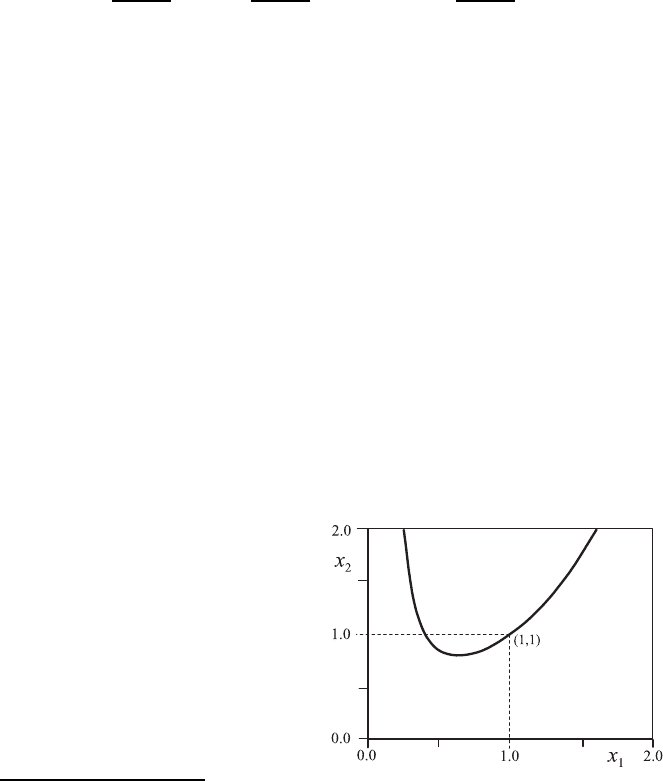
This path line is presented in Fig. 4.3.

Fig. 4.3 Path line of the ﬂuid ﬂow in

the plane x

−x

Attention is drawn to the fact that this ﬂow ﬁeld is not source-free, thus it violates

the requirements of the continuity equation. This is, however, insigniﬁcant for the

purely kinematic considerations mentioned here.

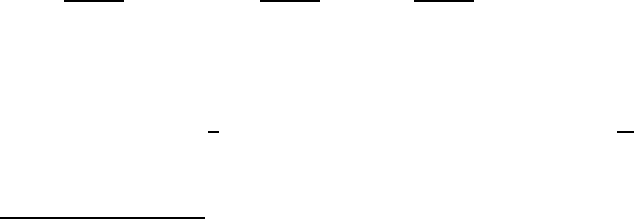
90 4 Basics of Fluid Kinematics

4.3.2 Streak Lines of Local ly Injected Tracers

As mentioned before, it is usual in experimental ﬂuid mechanics to gain

qualitative insight into a ﬂow process by the injection, at a ﬁxed location,

of a continuous ﬂuid tracer. This leads to a marked “ﬂuid thread” which is

carried with the ﬂow and thus marks the course of the ﬂow. This is called

a streak line. When the exact course of the ﬂow is of interest, quantitative

evaluations of the location coordinates of streak lines of locally installed tracer

materials are required. These evaluations can, based on the derivations stated

below, be carried out with methods of ﬂow kinematics.

A ﬂuid particle marked with a tracer, e.g. an air particle or any other gas

particle marked with smoke, or a water or liquid particle marked with color,

which at time t is located at the position {x

} = {x

(t)}



must have passed

the injection point for the tracer at a moment in time (t −τ), in order to be

present as a marked particle at the point { x

}, i.e. the following relationship

holds

(t)}



= {x

(t − τ )}

(4.24)

Hence the streak line covered by marked ﬂuid elements up to time t can

be computed as the path line of the ﬂuid elements that fulﬁlls the condi-

tion (4.24). A path line needs to be computed with the initial condition that

for t = τ the ﬂuid element held the position of the location coordinates of the

injection point of the tracers. The streak line is thus composed of the sum

of the path lines of individual particles. For each individual marked particle

of a streak line a parameter τ is introduced, which for 0 ≤ τ ≤ t covers all

parts of a sweeping path. It is therefore important to vary the parameter τ

in the solution equations in order obtain the entire streak line.

The above short explanations will be made clearer by way of an example,

which is handled on the basis of the three-dimensional velocity ﬁeld also used

above:

= x

(1 + t),U

= −x

and U

= −x

t (4.25)

This velocity ﬁeld yields the set of diﬀerential equations for the motion of a

ﬂuid element in space, i.e. the following diﬀerential equations:

d(x

)

= x

(1 + t),

d(x

)

= −x

d(x

)

= −x

t. (4.26)

As a solution one obtains the components (x

)

, (x

)

and (x

)

according

to (4.13):

)

= C

exp



t(1 +

)



, (x

)

= C

exp[−t], (x

)

= C

exp



−



(4.27)

The subscript s signiﬁes that the location coordinate of the sweeping path is meant.

4.3 Motion of Fluid Elements 91

If one inserts the initial conditions, that (x

)

=(x

)

t=τ

=1, (x

)

t=τ

=1, (x

)

=(x

)

t=τ

= 1 the injection condition for t = τ, i.e. that

the position (1, 1, 1) serves as an injection point of the tracer, one obtains:

=exp



−τ(1 +

)



=exp[τ]andC

=exp





(4.28)

Inserting in this result the solutions for (x

)

, (x

)

and (x

)

the equation

for the space coordinates for the streak line results for all times

)

=exp







− τ







)

=exp[−(t − τ)], (4.29)

)

=exp



−

− τ

)



When one wants to make the spatial course of a streak line visible at a

moment in time t, one has to insert the value of t in the above equation. In

this way one obtains the equation of a space curve, with τ as a parameter.

Here τ is determined by the period of time [τ

,τ

] of the tracer injection in

(1, 1, 1) with −∞ <τ

<τ

<t.Forτ

→−∞,τ

= t and t = 0 one can

write:

)

=exp



−τ





)

=exp[τ ] −∞<τ<0 (4.30)

)

=exp





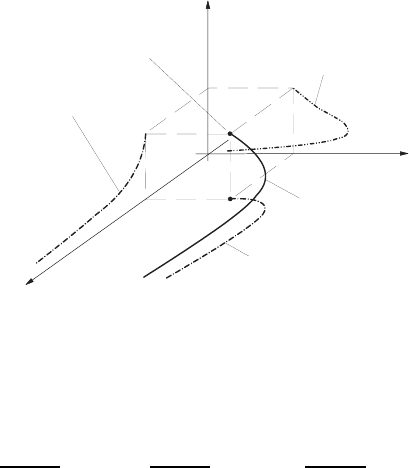
The course of this space curve is shown in Fig. 4.4. It indicates the streak

line existing at the moment in time t = 0 (made visible from τ = −∞ to

τ = 0). In Fig. 4.4 the projections of the streak line into the main level of the

Cartesian coordinate system are also introduced.

When one compares the equation for the streak line ﬁxed by the space

point (1, 1, 1) with the equations for the path line of a ﬂuid element, stated

for the same ﬂow ﬁeld, one realizes that path lines and streak lines are not

identical for non-stationary ﬂows. Only in the case of a stationary ﬂow are

path lines and streak lines identical, as can be shown easily by the following

considerations.

Considering the stationary velocity ﬁeld:

=2x

= −x

(4.31)

As a space curve is involved here, the statement in x

-coordinates is appro-

priate. The deﬁnition x

indicates that the location coordinates of a streak line

are meant.

92 4 Basics of Fluid Kinematics

(1,1,1)

Point of injection

-x

projection

of steak line

Streak line

-x

projection

of steak line

-x

projection

of steak line

Fig. 4.4 Streak line for the time t = 0, with ﬂuid tracer injections between τ = −∞

and τ = 0 at the position (1, 1, 1)

one obtains for the path line of a ﬂuid element the following diﬀerential

equations:

d(x

)



=2x

d(x

)



= −x

d(x

)



= −x

(4.32)

For t = 0 it will be assumed that (x

)



=(x

)



=(x

)



= 1 so that in the

solution

)



= C

exp[2t] , (x

)



= C

exp[−t] , (x

)



= C

exp[−t] (4.33)

holds and thus the path line for a marked tracer  canbeexpressedasfollows:

)



=exp[2t] , (x

)



=exp[−t] , (x

)



=exp[−t] (4.34)

with −∞ <t<∞. For the computation of the streak lines the solution in

(4.27) can be employed again and C

, and C

can be computed such that

it is claimed that at time t = τ the following relationship holds:

(t = τ))

=1, (x

(t = τ))

=1, (x

(t = τ))

= 1 (4.35)

Therefore, it can be deduced that

=exp[−2τ],C

=exp[τ] ,C

=exp[τ] (4.36)

or as the coordinate for the streak line for each time t:

)

=exp[2(t − τ)] , (x

)

=exp[−(t − τ)] , (x

)

=exp[−(t − τ)]

(4.37)

where the range of the values of τ is deﬁned by the period of time of the

tracer injection. In the case that the tracer substance is injected at all

4.3 Motion of Fluid Elements 93

(1,1)

2.0

1.0

0.0

1.0

2.0

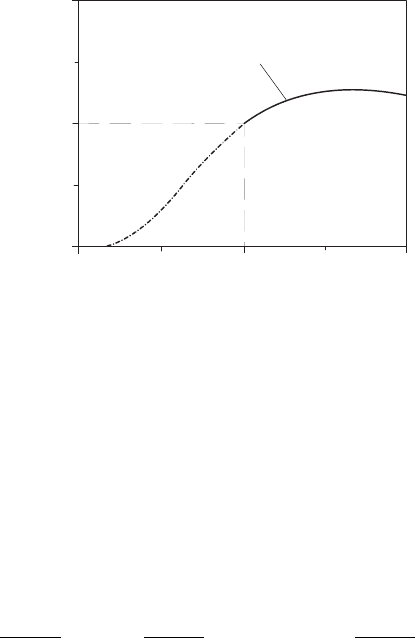
Streak line

Fig. 4.5 Streak line in the plane x

−x

(the full drawn line corresponds to −∞ ≤

τ ≤ 0, broken line to 0 ≤ τ ≤∞)

times, i.e. −∞ <τ<∞, (4.34) and (4.37) yield the same curve. When

the tracer injection is limited to certain time periods, one obtains as a visi-

ble streak line equation (4.37) only the corresponding part of the path line

equation (4.34), see Fig. 4.5.

When one repeats the above derivations for the two-dimensional velocity

ﬁeld also stated in Sect. 4.3.1:

= x

(1 + 2t),U

= 0 (4.38)

which leads to the diﬀerential equations (4.19):

d(x

)



= x



d(x

)



= x



(1 + 2t),

d(x

)



= 0 (4.39)

with the solution

)



= C

exp[t] , (x

)



= C

exp[t(t +1)], (x

)



= C

(4.40)

On the other hand, when one demands that for the particle located at time

t at the point x

passes the injection point (1, 1, 0) of a tracer at the

moment in time τ, the integration constants C

and C

can be obtained

from the following conditional equations:

exp[τ]=1,C

exp[τ(τ +1)]=1,C

= 0 (4.41)

These “constants” can now be inserted in (4.40) again, where C

=0signiﬁes

that the streak line lies in the plane x

−x

, i.e. in the plane x

=0,andis

described there by the following equations for the position coordinates (x

)

and (x

)

=exp[t − τ], (x

)

=exp[t(t +1)− τ(τ + 1)] (4.42)

94 4 Basics of Fluid Kinematics

For the moment expressed by time t = 0, the course of the streak line is:

)

=exp[−τ]and

in the domain −∞<τ <∞

)

=exp[−τ(τ +1)]

(4.43)

From the equation for (x

)

, it follows that:

τ = −ln(x

)

(4.44)

Inserted in the equation for (x

)

at time t = 0, the existing course of the

streak line made visible by the injection of tracer material in −∞ <τ<∞

results for the plane x

−x

)

=(x

)

(1−ln(x

)

in the domain 0 < (x

)

< ∞

)

=[(x

)

]

(

1−ln(x

)

(4.45)

4.4 Kinematic Quantities of Flow Fields

4.4.1 Stream Lines of a Velocity Field

The considerations in Sect. 4.3 for ﬂuid elements, i.e. for the computation of

path lines and streak lines have to be separated strictly from considerations

for the determination of the stream lines of a ﬂow ﬁeld. Although for station-

ary ﬂows stream lines, path lines and streak lines are identical, this does not

justify neglecting the fundamental diﬀerences, or even worse, assuming that

such diﬀerences do not exist. Only by a clear separation of the considerations

does it become generally comprehensible why under the steady-state condi-

tions of a ﬂow ﬁeld the above-stated identities of stream lines, path lines and

streak lines exist.

If one considers the non-stationary ﬂow ﬁeld U

,t), stream lines can

be deﬁned for this ﬁeld at any moment in time t, so that space curves run

parallel to the velocity vectors. The latter are deﬁned as stream lines at each

point of the velocity ﬁeld. In the case that one considers initially a two-

dimensional ﬂow ﬁeld, for which all velocity vectors lie parallel to the plane

−x

, then the above deﬁnition of the stream line leads to the following

deﬁning equation:

d(x

)

d(x

)

for time t = constant (4.46)

This relationship means that the gradient of the stream line is equal to the

tangent of the angle formed by the velocity vector with the axis x

at the

instant in time t; see Fig. 4.6. The index ψ in (4.46) indicates that the stated

coordinates x

−x

describe the stream line ψ =const.