Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows
Подождите немного. Документ загружается.


74 3 Physical Basics
• Mass conservation law (continuity equation)
• Momentum conservation law (equation of momentum)
• Energy conservation law (energy equation)
• Conservation of chemical species
• State equations
These basic laws can now be applied to several “balance domains”. The size of
the balance space is not important in general and it can include infinitesimally
small balance domains (differential considerations) or finite volumes (integral
considerations). Furthermore, the balance domains can lie at a fixed location
in different coordinate systems and can undergo motions themselves (Euler
and Lagrangian approaches). In general, once selected, domains for balance
considerations are usually maintained for all quantities to be considered, i.e.
mass, momentum, energy, etc.; however, this is not necessary. Changes in
domains are admissible as long as they are known and thus can be included
in the balance considerations.
Generally, to derive the basic fluid flow equations in fluid mechanics, only
integral considerations are made, but balance considerations are made over
different domains of interest. In the case of differential considerations, one
finds balance considerations for moving fluid elements (Lagrangian approach)
or space fixed elements (Eulerian approach). The two ways of fluid flow de-
scription have to be clearly distinguished and balances should always be set
up separately for the Lagrangian and Eulerian balance spaces. Mixed bal-
ances leads to errors, in general. However, transformations of final equations
are possible. It is usual, for example, in fluid mechanics to transform the
balance relationships derived for a moving fluid element to space-fixed co-
ordinate systems and thus to obtain balance relations for constant volumes.
The connections between considerations for moving fluid elements and space-
fixed control volume in this book are presented and the equations required for
the transformation are derived. Particular attention is given to the physical
understanding of the principal connections, so that advantages and disad-
vantages of the different approaches become clear. The advantages of the
“Eulerian form” of the basic equations are brought out with respect to the
imposed boundary conditions for obtaining solutions to flow problems. On
the other hand, the Lagrangian considerations allow the transfer of often
known physical knowledge of mechanics of moving bodies to fluid mechanics
considerations.
When stating the basic equations in Lagrange variables, the following
equations are valid for a fluid element:
3
• Mass conservation:
d(δm)
dt
=0
3
The derivation of these equations is presented in Chap. 5. They are stated here
beforehand to explain the basic physical knowledge that is taken from Physics.
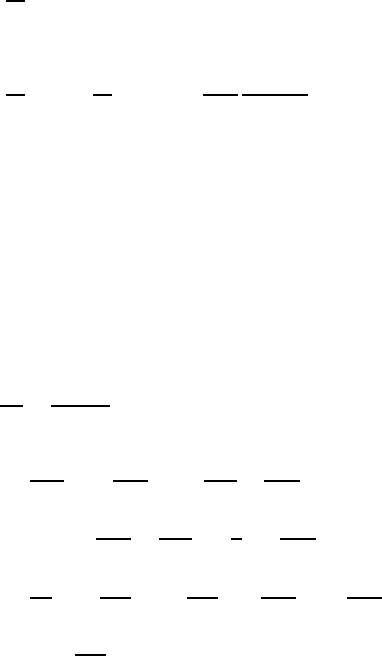
3.5 Balance Considerations and Conservation Laws 75
• Newton’s 2nd law:
d
dt
[(δm)
(U
j
)
]=
(δM
j
)
+(δ
˙
J
j
)
+
(δO
j
)
• Energy conservation:
d
dt
(e)
=
d
dt
(˙q)
− P
1
δV
d(δV )
dt
+ φ
diss
• State equation: e
= f(P
,T
)andP
= f(ρ
,T
)
(3.69)
The above representations make it clear that, generally, in fluid mechanics,
considerations agree with principles that are usually applied in thermodynam-
ics, e.g. the energy equation (1st law of thermodynamics) and state equations
for liquids and gases.
As is shown in Chap. 5, the above equations can also be expressed in
field variables, such that the following set of differential equations for density
ρ(x
i
,t), pressure P (x
i
,t), temperature T (x
i
,t), internal energy e(x
i
,t), and
three velocity components U
j
(x
i
,t)(j =1, 2, 3) are obtained:
• Mass conservation:
∂ρ
∂t
+
∂(ρU
i
)
∂x
i
=0
• Newton’s 2nd law: ρ
∂U
j
∂t
+ U
i
∂U
j
∂x
i
= −
∂P
∂x
j
−
∂τ
ij
∂x
i
+ ρg
i
with τ
ij
= −µ
∂U
j
∂x
i
+
∂U
i
∂x
j
+
2
3
µδ
ij
∂U
k
∂x
k
• Energy conservation: ρ
∂e
∂t
+ U
i
∂e
∂x
i
= −
∂ ˙q
i
∂x
i
− P
∂U
j
∂x
j
− τ
ij
∂U
j
∂x
i
with ˙q
i
= −λ
∂T
∂x
i
• State equations: e = f(P, T )andP = f(ρ, T )
(3.70)
Thus five differential equations are available, if one inserts τ
ij
and ˙q
i
through
the above equations, for altogether seven unknowns and two thermodynamic
equations. With this, the closed system of differential equations given above
can be solved for specified initial and boundary conditions. Therefore, the
given flow problem is defined by its initial and boundary conditions, needed
for the solution of the above set of equations. The basic physical laws are
identical for all flow problems. They comprise, as said above, the conservation
and state equations that are usually treated in thermodynamics. Therefore,
a repetition of thermodynamic fundamentals is essential as summarized in
Sect. 3.6.
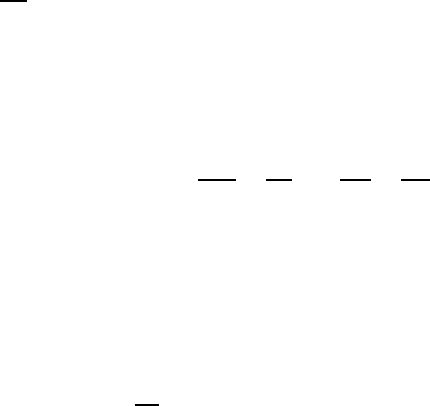
76 3 Physical Basics
3.6 Thermodynamic Considerations
The thermodynamic state equations of fluids are often used as a supplement
for the solution of flow problems. However, in the present text only “simple
fluids”, i.e. homogeneous liquids and gases for which the thermodynamic
state can be expressed by a relation between pressure, temperature, and
density, are considered. Hence the following statements are possible for both
substantial and field quantities, i.e.:
P
= f(T
,ρ
)orP = f(T,ρ) (3.71)
The thermodynamic state equations for simple fluids are known to be:
P
ρ
= RT
(thermodynamically ideal gases)
ρ
= constant (thermodynamically ideal liquids).
If one defines α
= P
,T
,ρ
,e
and α = P,T,ρ,e,..., the following
relation holds when the fluid element is located at time t at position x
i
(see Sect. 2.6):
α
(t)=α(x
i
,t) ;
dα
dt
=
∂α
∂t
+ U
i
∂α
∂x
i
=
Dα
Dt
. (3.72)
The second part of (3.72) indicates how temporal changes of substantial,
thermodynamic quantities can be computed from the substantial derivative
of corresponding field quantities.
In addition to the above thermodynamic state properties P
,T
,ρ
,
e
,..., other state properties can be defined whose introduction is of ad-
vantage in certain thermodynamic considerations. Some of them are as
follows:
• Specific volume: υ
=
1
ρ
• Enthalpy: h
= e
+ P
υ
• Free energy: f
= e
− T
s
(Helmholtz potential)
• Free enthalpy: g
= h
− T
s
(Gibb potential)
Accordingly, it is possible to apply certain mathematical operators in or-
der to define “new thermodynamic quantities”. However, their introduction
makes sense, i.e. considerations become simpler or easier when carried out
with newly introduced quantities. Advantages result from the introduction
of newly defined quantities into thermodynamic considerations.
In one of the above definitions of thermodynamic potentials, the entropy
s
was used, whose definition is given by a differential relationship:
T
ds
=de
+ P
dυ
(Gibbs relationship). (3.73)
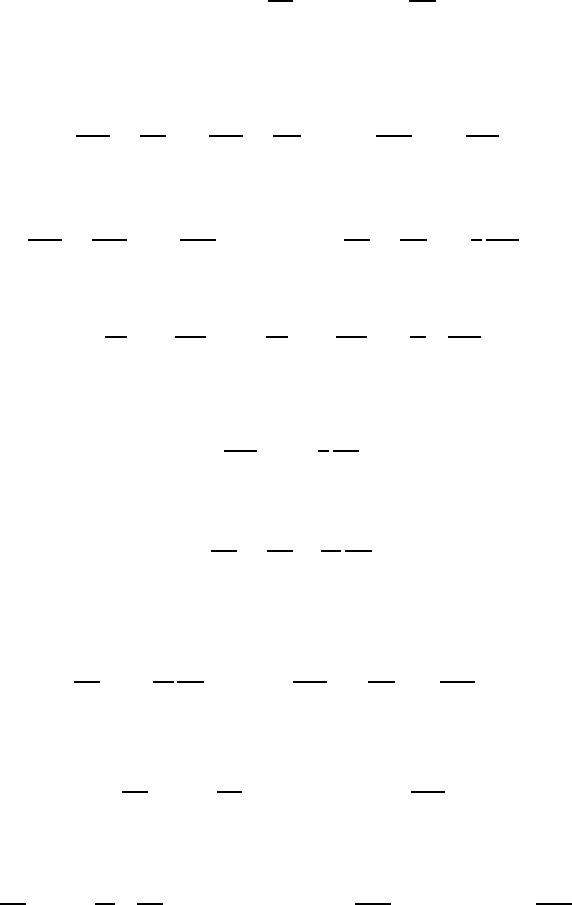
3.6 Thermodynamic Considerations 77
Integrating, one obtains:
s
= s
()
0
+
#
e
(e
)
0
1
T
de
+
#
υ
(υ
)
0
P
T
dυ
. (3.74)
Equations (3.73) and (3.74) can be understood as identical definitions for the
entropy s
of a fluid element. When employing (3.72) one obtains with:
ds
dt
=
Ds
Dt
de
dt
=
De
Dt
and
dυ
dt
= υ
∂U
i
∂x
i
(3.75)
the following relationships:
T
ds
dt
=
de
dt
+ P
dυ
dt
; T
Ds
Dt
=
De
Dt
+ P
1
ρ
∂U
i
∂x
i
(3.76)
or
T
∂s
∂t
+ U
i
∂s
∂x
i
=
∂e
∂t
+ U
i
∂e
∂x
i
+
P
ρ
∂U
i
∂x
i
. (3.77)
When one applies the mass conservation equation (3.70), it can be rearranged
further to yield:
∂U
i
∂x
i
= −
1
ρ
Dρ
Dt
. (3.78)
Insertion in (3.76) yields
T
Ds
Dt
=
De
Dt
−
P
ρ
2
Dρ
Dt
. (3.79)
From this relation, further equations can be derived that are important in
fluid mechanics, e.g. for s
= constant:
De
Dt
s
=
P
ρ
2
Dρ
Dt
;
de
dt
s
P
ρ
2
=
de
dρ
s
. (3.80)
For ρ
= constant or υ
= constant:
T
Ds
Dt
ρ
=
De
Dt
ρ
; T
=
de
ds
ρ
(3.81)
Further, for e
= constant:
T
Ds
Dt
e
= −
P
ρ
2
Dρ
Dt
e
; P
= T
∂s
∂υ
e
= −T
ρ
2
∂s
∂ρ
e
(3.82)
Further significant relationships, known from the field of thermodynamics,
are needed in the following forms:
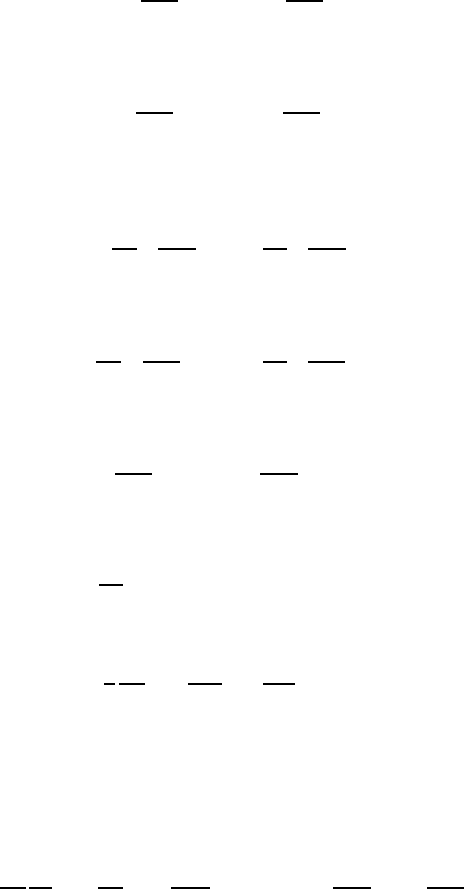
78 3 Physical Basics
• Specific heat capacity of a fluid at constant volume:
c
v
=
∂e
∂T
υ
= T
∂s
∂T
υ
(3.83)
• Specific heat capacity of a fluid at constant pressure:
c
p
=
∂h
∂T
P
= T
∂s
∂T
P
, (3.84)
where h
= e
+ P
υ
.
• Isothermal compressibility coefficient:
α = −
1
υ
∂υ
∂P
T
=
1
ρ
∂ρ
∂P
T
(3.85)
• Thermal expansion coefficient:
β =
1
υ
∂υ
∂T
P
= −
1
ρ
∂ρ
∂T
P
(3.86)
When one takes into account the following relationship:
dρ
=
∂ρ
∂T
P
dT
+
∂ρ
∂P
T
dP
(3.87)
including (3.85) and (3.86), the following relation can be formulated for all
fluids:
1
ρ
dρ
= αdP
− βdT
(3.88)
or, rearranged in terms of field variables:
1
ρ
Dρ
Dt
= α
DP
Dt
− β
DT
Dt
. (3.89)
This relation allows the statement that all fluids of constant density, i.e.
fluids having the property ρ
= constant or (Dρ/Dt) = 0, can be designated
as incompressible. They react neither to pressure variations (α =0)norto
temperature variations (β = 0) with changes in volume or density.
For any fluid, the difference in the heat capacities is given by
(c
p
− c
υ
)=
T
ρ
β
2
α
= −
T
ρ
· β
∂P
∂T
ρ
= −T
∂P
∂T
ρ
∂υ
∂T
P
.
(3.90)
The above general relationships (3.85) and (3.86) can now be employed to
derive the special α and β equations below that hold for the two thermo-
dynamic ideal fluids that receive special attention in this book, namely the
3.6 Thermodynamic Considerations 79
ideal gas and the ideal liquid. For an ideal gas:
P
ρ
= RT
and consequently
P
ρ
= RT (3.91)
and in addition
∂e
∂υ
T
=
∂e
∂P
T
=0andc
v
= constant, i.e. the internal
energy of an ideal gas is a pure function of the temperature. The isother-
mal compressibility coefficient α and the thermal expansion coefficient β are
given by:
α =
1
ρ
∂ρ
∂P
T
=
1
ρ
1
RT
=
1
P
β = −
1
ρ
∂ρ
∂T
P
= −
1
ρ
−
P
RT
2
=
1
T
(3.92)
and therefore the difference in the specific heat capacities for an ideal gas is:
c
p
− c
v
=
T
ρ
1
T
2
P
=
P
ρ
T
= R. (3.93)
It can further be formulated for the change in density:
dρ
ρ
=
dP
P
−
dT
T
. (3.94)
If we introduce the thermodynamically ideal liquid that distinguishes itself
by α =0andβ = 0 , i.e. by:
dρ
ρ
= 0 (fluid of constant density) (3.95)
we obtain the difference in the heat capacities and it can be computed that:
c
p
− c
v
= −
T
ρ
β
∂P
∂T
ρ
with β =0 ; c
p
= c
v
. (3.96)
When one employs the Gibbs relationship, (3.73), dρ
=
1
dυ
=0,one
obtains:
∂s
∂e
ρ
=
1
T
. (3.97)
Because s
= f(p
), the pressure in an ideal liquid does not need to be taken
into account as a thermodynamic quantity. It exists as a mechanical quantity,
but for an ideal fluid it is not part of a thermodynamic state equation.
A further physical property of a fluid, which is of significance when deal-
ing with some of the flow problems presented in this book, is the velocity
80 3 Physical Basics
propagation of small pressure perturbations, the so-called sound velocity:
c
2
=
∂P
∂ρ
s
. (3.98)
This quantity is defined as isentropic pressure change with density change, the
entropy being maintained constant. Hence the propagation of small acoustic
perturbations takes place isentropically.
If one takes into account the following relationship for the cited sequence
of partial derivations:
1=
∂T
∂e
ρ
∂e
∂s
ρ
∂s
∂T
ρ
(3.99)
and if one considers:
T
=
∂e
∂s
ρ
c
v
=
∂e
∂T
ρ
(3.100)
then
c
v
= T
∂s
∂T
ρ
. (3.101)
Also taking into account the Maxwell relations:
∂T
∂ρ
s
=
1
ρ
2
∂P
∂s
ρ
(3.102)
∂ρ
∂s
T
= − ρ
2
∂T
∂P
ρ
(3.103)
it can be formulated that:
∂s
∂T
ρ
∂T
∂ρ
s
∂ρ
∂s
T
= −1 (3.104)
and one can also express the quantity c
v
as:
c
v
= −T
∂ρ
∂T
s
∂s
∂ρ
T
. (3.105)
Similarly, it can be derived that:
c
p
= −T
∂P
∂T
s
∂s
∂P
T
. (3.106)
For the relationship of the heat capacities, it can be formulated that:
κ =
c
p
c
v
=
∂P
∂T
s
∂s
∂P
T
∂ρ
∂T
s
∂s
∂ρ
T
=
∂P
∂ρ
s
∂ρ
∂P
T
. (3.107)

References 81
With the definition equation for the speed of sound and the isothermal
compressibility coefficient, one obtains
c
2
= κ
∂P
∂ρ
T
=
κ
ρ
α
. (3.108)
For an ideal gas with α =
1
P
and considering the ideal gas equation yields
c =
κR
T
. (3.109)
For an ideal liquid with α → 0
c →∞, (3.110)
i.e. for a fluid with constant density an infinitely large sound velocity results.
References
3.1. Bird, R.B., Stewart, W.E., Lightfoot, E.N., Transport Phenomena, Wiley, New
York, 1960.
3.2. Reif, F., Physikalische Statistik und Physik der W¨arme, Walter de Gruyter,
Berlin, 1976.
3.3. H¨ofling, O., Physik: Lehrbuch f¨ur Unterricht und Selbststudium, D¨ummler,
Bonn, 1994.
3.4. Bosnjakovic, F., Technische Thermodynamik, Theodor Steinkopf, Dresden, 1965.
3.5. Hirschfelder, J.O., Curtiss, C.F., Bird, R.B., Molecular Theory of Gases and
Liquids, Wiley, New York, 1963.
3.6. Kienan
3.7. Present, R.D., Kinetic Theory of Gases, McGraw-Hill, New York, 1958.
3.8. Chapman, S., Cowling, T.G., The Mathematical Theory of Non-uniform Gases,
Cambridge University Press, Cambridge, 1960.
Chapter 4
Basics of Fluid Kinematics
4.1 General Considerations
The previous chapters dealt with important basic knowledge and information
of mathematics and physics as applied in the field of fluid mechanics. This
knowledge is needed to describe fluid flows or derive and utilize the basic
equations of fluid mechanics in order to solve flow problems. In this respect,
it is important to know that fluid mechanics is primarily interested in the
velocity field U
j
(x
i
,t), for given initial and boundary conditions, and in the
accompanying pressure field P (x
i
,t), i.e. fluid mechanics seeks to present and
describe flow processes in field variables. This presentation and description
result in the “Eulerian form” of considerations of fluid flows. This form is
best suited for the solution of flow problems and is thus mostly applied in
experimental, analytical and numerical fluid mechanics. Thanks to the intro-
duction of field quantities also for the thermodynamic properties of a fluid,
e.g. the pressure P (x
i
,t) and the temperature T (x
i
,t), the density ρ(x
i
,t)
and the internal energy e(x
i
,t), and for the molecular transport quantities,
e.g. the dynamic viscosity µ(x
i
,t), the heat conductivity λ(x
i
,t)andthe
diffusion coefficients D(x
i
,t), a complete presentation of fluid mechanics is
possible. With the inclusion of diffusive transport quantities, i.e. the molec-
ular heat transport ˙q
i
(x
i
,t), the molecular mass transport ˙m
i
(x
i
,t)andthe
molecular momentum transport τ
ij
(x
i
,t), it is possible to formulate the con-
servation laws for mass, momentum and energy for general application. The
basic equations of fluid mechanics can thus be formulated locally, as is shown
in Chap. 5, and hold for all flow problems in the same form. The differences in
the solutions of these equations result from the different initial and boundary
conditions that define the actual flow problems. These enter into the solutions
by the integration of the locally formulated basic fluid flow equations.
Experience shows that the derivation of the basic equations of fluid me-
chanics can be achieved in the easiest way by considering fluid elements, i.e.
by employing the “Lagrangian considerations” for the derivation of the flow
equations. The Lagrange approach starts from the assumption that a fluid
83
84 4 Basics of Fluid Kinematics
can be split up, at a fixed time t = 0, into “marked elements” with mass δm
,
pressure P
, temperature T
,densityρ
, internal energy e
,etc.Anelement
with the index possesses also a velocity (U
j
)
, which is defined as the La-
grangian velocity of the marked element. This velocity is always linked to
the fluid element marked with and to all other quantities labelled with .
In fluid mechanics, these quantities are also designated as substantial prop-
erties and are best employed to derive the basic laws of fluid mechanics in
an easily comprehensible way. As the following considerations will show, the
basic knowledge of mechanics, gained in physics, can be transferred into fluid
mechanics in the simplest way when it is introduced by way of Lagrangian
considerations, yielding the basic equations for fluid flows, deriving them for
a fluid element.
4.2 Substantial Derivatives
If one defines α
, a substantial quantity such as P
, T
, ρ
and e
,the
derivations of equations in fluid mechanics often require the total differential
dα
to be employed:
dα
=
∂α
∂t
dt +
∂α
∂x
1
(dx
1
)
+
∂α
∂x
2
(dx
2
)
+
∂α
∂x
3
(dx
3
)
(4.1)
where α(x
i
,t) is the field variable corresponding to α
.
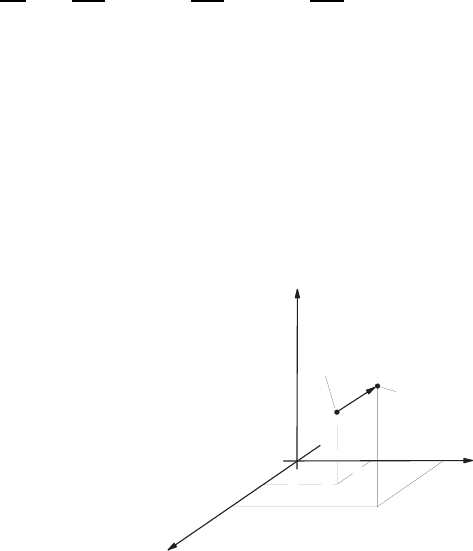
The fluid element motion in space (Fig. 4.1) can be described as follows:
(dx
1
)
=(U
1
)
dt = U
1
dt
(dx
2
)
=(U
2
)
dt = U
2
dt
(dx
3
)
=(U
3
)
dt = U
3
dt
(4.2)
The replacement of the substantial velocities (U
i
)
by the field quantities
U
i
in (4.2) is permissible, as at the time t we assume (x
i
)
= x
i
and thus
(U
i
)
(t)=U
i
(x
i
,t). Therefore, the following relationship holds:
Fig. 4.1 Motion of a fluid element in
space
Fluid element
at time t
Fluid element
at time (
t+
d
t
)
x
2
x
1
x
3
