Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows
Подождите немного. Документ загружается.

44 2 Mathematical Basics
Many of the properties of the above functions are similar to those of real
trigonometric functions. Thus it can be shown that
sin
2
z +cos
2
z =1;1+tan
2
z =sec
2
z;1+cot
2
z =csc
2
z (2.129)
sin(−z)=−sin z;cos(−z)=cosz;tan(−z)=−tan z (2.130)
sin(z
1
± z
2
)=sinz
1
cos z
2
± cos z
1
sin z
2
(2.131)
cos(z
1
± z
2
)=cosz
1
cos z
2
∓ sin z
1
sin z
2
(2.132)
tan(z
1
± z
2
)=
tan z
1
± tan z
2
1 ∓ tan z
1
tan z
2
(2.133)
Hyperbolic Functions
The hyperbolic functions in the complex case are defined as follows:
sinh z =
e
z
− e
−z
2
cosh z =
e
z
+ e
−z
2
(2.134)
sech z =
1
cosh z
=
2
e
z
+ e
−z
csch z =
1
sinh z
=
2
e
z
− e
−z
(2.135)
tanh z =
sinh z
cosh z
=
e
z
− e
−z
e
z
+ e
−z
coth z =
cosh z
sinh z
=
e
z
+ e
−z
e
z
− e
−z
(2.136)
For these functions, the following relations apply:
cosh
2
z − sinh
2
z =1;1− tanh
2
z =sech
2
z;coth
2
z −1 = csch
2
z (2.137)
sinh(−z)=−sinh z;cosh(−z)=coshz; tanh(−z)=−tanh z (2.138)
sinh(z
1
± z
2
)=sinhz
1
cosh z
2
± cosh z
1
sinh z
2
(2.139)
cosh (z
1
± z
2
)=coshz
1
cosh z
2
± sinh z
1
sinh z
2
(2.140)
tanh(z
1
± z
2
)=
tanh z
1
± tanh z
2
1 ± tanh z
1
tanh z
2
(2.141)
From the above relations for trigonometric functions and hyperbolic
functions, the following connections can be indicated:
sin iz = i sinh z cos iz =coshz tan iz = i tanh z (2.142)
sinh iz = i sin z cosh iz =cosz tanh iz = i tan z (2.143)

2.11 Complex Numbers 45
Logarithmic Functions
As in the real case, the natural logarithm is the inverse function of the
exponential function, i.e. it holds for complex cases that
F (z)=lnz =lnr + i(ϕ +2kπ) k =0, ±1, ±2,... (2.144)
where z = re
iϕ
holds. It appears that the natural logarithm represents a
non-equivocal function. By limitation to the so-called principal value of the
function, an equivocalness can be produced. Here a certain arbitrariness
is given. It can be eliminated by a specially desired branch, on which the
equivocalness is guaranteed, which is also indicated, for example by (ln z)
0
.
The logarithmic functions can be defined for any real basis, i.e. also for
values that differ from e. This means that the following can be stated:
F (z) = log
a
z ⇔ z = a
F
(2.145)
where
a>0aswellasa =0 and a = 1 (2.146)
Inverse Trigonometric Functions
Inverse trigonometric functions for complex numbers can be stated as follows.
These functions also are defined as non-equivocal, but show a periodicity:
sin
−1
z = i ln
iz +
1 − z
2
csc
−1
z =
1
i
ln
*
i +
√
z
2
− 1
z
+
(2.147)
cos
−1
z = i ln
z +
z
2
− 1
sec
−1
z =
1
i
ln
*
1+
√
1 − z
2
z
+
(2.148)
tan
−1
z =
1
2i
ln
1+iz
1 − iz
cot
−1
z = −
1
2i
ln
iz +1
iz −1
(2.149)
Inverse Hyperbolic Functions
Analogous to the considerations of the trigonometric functions, the inverse
functions of the hyperbolic functions can be formulated. These are as follows:
sinh
−1
z =ln
z +
z
2
+1
csch
−1
z =ln
*
i +
√
z
2
+1
z
+
(2.150)
cosh
−1
z =ln
z +
z
2
− 1
sech
−1
z =ln
*
1+
√
1 − z
2
z
+
(2.151)

46 2 Mathematical Basics
tanh
−1
z =
1
2
ln
1+z
1 − z
coth
−1
z =
1
2
ln
z +1
z − 1
(2.152)
Differentiation of Complex Functions
(Cauchy–Riemann Equations)
If the function F (z)inafieldG ∈ C is defined and the limiting value
F
(z) = lim
∆z→0
F (z + ∆z) − F (z)
∆z
(2.153)
is independent of the approximation ∆z → 0, then the function F (z)inthe
field G is designated analytically.
A necessary condition so that the function F (z)=Φ + iΨ represents a
function analytically in G ∈ C is set by the Cauchy–Riemann differential
equations:
∂Φ
∂x
=
∂Ψ
∂y
∂Φ
∂y
= −
∂Ψ
∂x
(2.154)
When the partial derivations of the Cauchy–Riemann equations in G are
steady, then the Cauchy–Riemann equations are a sufficient condition to say
that F (z) is analytical in the field G.
From the Cauchy–Riemenn relations, it can be derived by differentiation
that the real and imaginary parts of the function F (z), i.e. the quantities
Φ(x, y)andΨ(x, y), fulfill the Laplace equation, i.e.
∂
2
Φ
∂x
2
+
∂
2
Φ
∂y
2
= 0 (2.155)
∂
2
Ψ
∂x
2
−
∂
2
Ψ
∂y
2
= 0 (2.156)
Differentiation of Complex Functions
If F (z), G(z)andH(z) are analytical functions of the complex variable z,
then the differentiation laws of the functions result as indicated below. It is
easy to see that they are analogus to the function of real variables.
d
dz
[F (z)+G(z)] =
d
dz
F (z)+
d
dz
G(z)=F
(z)+G
(z) (2.157)
d
dz
[F (z) − G(z)] =
d
dz
F (z) −
d
dz
G(z)=F
(z) − G
(z) (2.158)
d
dz
[cF (z)] = c
d
dz
F (z)=cF
(z), with c as arbitrary constant (2.159)
d
dz
[F (z)G(z)] = F (z)
d
dz
G(z)+G(z)
d
dz
F (z)=F (z)G
(z)+G(z)F
(z)
(2.160)

References 47
d
dz
F (z)
G(z)
=
G(z)
d
dz
F (z) − F (z)
d
dz
G(z)
[G(z)]
2
=
G(z)F
(z) − F (z)G
(z)
[G(z)]
2
G(z) = 0 (2.161)
When W = F (ζ)andζ = G(z)
dW
dz
=
dW
dζ
dζ
dz
= F
(ζ)
dζ
dz
= F
[G(z)]G
(z) (2.162)
The following table represents the important derivations of complex func-
tions:
d
dz
(c)=0
d
dz
z
n
= nz
n−1
d
dz
e
z
= e
z
d
dz
a
z
= a
z
ln a
d
dz
sin z =cosz
d
dz
cos z = − sin z
d
dz
tan z =sec
2
z
d
dz
cot z = − csc
2
z
d
dz
sec z =secz tan z
d
dz
csc z = − csc z cot z
d
dz
log
e
z =
d
dz
ln z =
1
z
d
dz
log
a
z =
1
z ln a
d
dz
sin
−1
z =
1
√
1−z
2
d
dz
cos
−1
z =
−1
√
1 − z
2
d
dz
tan
−1
z =
1
1+z
2
d
dz
cot
−1
z =
−1
1+z
2
d
dz
sec
−1
z =
1
z
√
z
2
− 1
d
dz
csc
−1
z =
−1
z
√
z
2
−1
d
dz
sinh z =coshz
d
dz
cosh z =sinhz
d
dz
tanh z =sech
2
z
d
dz
coth z = csch
2
z
d
dz
sech z = − sech z tanh z
d
dz
csch z = − csch z coth z
d
dz
sinh
−1
z =
1
√
1+z
2
d
dz
cosh
−1
z =
1
√
z
2
− 1
d
dz
tanh
−1
z =
1
1 − z
2
d
dz
coth
−1
z =
1
1 − z
2
d
dz
sech
−1
z =
−1
z
√
1 − z
2
d
dz
csch
−1
z =
−1
z
√
z
2
+1
(2.163)
The above derivations of important complex functions can be used for
dealing with potential flows.
References
2.1. Richter EW, Joos G (1978) H¨ohere Mathematik f¨ur den Praktiker. Barth, Leipzig
2.2. Gradshteyn IS, Ryzhik IM (1980) Table of Integrals, Series, and Products.
Academic press, San Diego
2.3. Gro¨smann S (1988) Mathematischer Einf¨uhrungskurs f¨ur die Physik. Teubner,
Stuttgart
48 2 Mathematical Basics
2.4. Aris R (1989) Vectors, Tensors and the Basic Equations of Fluid Mechanics,
Dover, New York
2.5. Meyberg K, Vachenauer T (1989) H¨ohere Mathematik 1 und 2. Springer-Verlag,
Berlin
2.6. Dallmann H, Elster KH (1991) Einf¨uhrung in die h¨ohere Mathematik 1–3. Gust
Fischer Verlag, Jena
2.7. Rade L, Westergren B (2000) Springers Mathematische Formeln. 3. Auflage
Springer-Verlag, Berlin
Chapter 3
Physical Basics
3.1 Solids and Fluids
All substances of our natural and technical environment can be subdivided
into solid, liquid and gaseous media, on the basis of their state of aggrega-
tion. This subdivision is accepted in many fields of engineering in order to
reveal important differences concerning the properties of the substances. This
subdivision could also be applied to fluid mechanics, but, it would not be par-
ticularly advantageous. It is rather recommended to employ fluid mechanics
aspects to achieve a subdivision of media, i.e. a subdivision appropriate for
the treatment of fluid flow processes. To this end, the term fluid is intro-
duced for designating all those substances that cannot be classified clearly
as solids. Hence, from the point of view of fluid mechanics, all media can be
subdivided into solids and fluids, the difference between the two groups being
that solids possess elasticity as an important property, whereas fluids have
viscosity as a characteristic property. Shear forces imposed on a solid from
outside lead to inner elastic shear stresses which prevent irreversible changes
of the positions of molecules of the solid. When, in contrast, external shear
forces are imposed on fluids, they react with the build-up of velocity gra-
dients, where the build-up of the gradient results via a molecule-dependent
momentum transport, i.e. momentum transport through fluid viscosity. Thus
elasticity (solids) and viscosity (liquids) are the properties of matter that are
employed in fluid mechanics for subdividing media. However, there are a few
exceptions to this subdivision, such as in the case of some of the materials
in rheology exhibiting mixed properties. They are therefore referred to as
visco-elastic media. Some of them behave such that for small deformations
they behave like solids and for large deformations they behave like liquids.
At this point, attention is drawn to another important fact regarding the
characterization of fluid properties. A fluid tries to evade the smallest external
shear stresses by starting to flow. Hence it can be inferred from this that a
fluid at rest is characterized by a state which is free of external shear stresses.
Each area in a fluid at rest is therefore exposed to normal stresses only.
49
50 3 Physical Basics
When shear stresses occur in a medium at rest, this medium is assigned to
solids. The viscous (or the molecular) transport of momentum observed in
a fluid, should not be mistaken to be similar to the elastic forces in solids.
The viscous forces cannot even be analogously addressed as elastic force.
This is the case for all liquids and gases as the two important subgroups of
fluids which take part in the fluid motions considered in the book. Hence
the present book is dedicated to the treatment of fluid flows of liquids and
gases. On the basis of these explanations of fluid flows, the fluids in motion
can simply be seen as media free from stresses and are therefore distinguished
from solids. The “shear stresses” that are often introduced when treating fluid
flows of common liquids and gases represent molecule-dependent momentum-
transport terms in reality.
Neighboring layers of a flowing fluid, having a velocity gradient between
them, do not interact with each another through “shear stresses” but through
an exchange of momentum due to the molecular motion between the layers.
This can be explained by simplified derivations aiming for a clear physical
understanding of the molecular processes, as stated in the following section.
The derivations presented below are carried out for an ideal gas, since they
can be understood particularly well for this case of fluid motion. The results
from these derivations therefore cannot be transferred in all aspects to fluids
with more complex properties.
For further subdivision of fluids, it is recommended to make use of their
response to normal stresses (or pressure) acting on fluid elements. When a
fluid element reacts to pressure changes by adjusting its volume and con-
sequently its density, the fluid is called compressible. When no volume or
density changes occur with pressure or temperature, the fluid is regarded as
incompressible although, strictly, incompressible fluids do not exist. However,
such a subdivision is reasonable and moreover useful and this will be shown
in the following derivations of the basic fluid mechanics equations. Indeed,
this subdivision mainly distinguishes liquids from gases.
In general, as said above, fluids can be subdivided into liquids and
gases. Liquids and some plastic materials show very small expansion co-
efficients (typical values for isobaric expansion are β
P
=10× 10
−6
K
−1
),
whereas gases have much larger expansion coefficients (typical values are
β
P
= 1,000 × 10
−6
K
−1
). A comparison of the two subgroups of fluids shows
that liquids fulfill the condition of incompressibility with a precision that is
adequate for the treatment of most flow problems. Based on the assumption
of incompressibility, the basic equations of fluid mechanics can be simpli-
fied, as the following derivations show; in particular, the number of equations
needed for the general description of fluid flow processes is reduced from 6
to 4. This simplification of the basic equations for incompressible fluid flows
allows a considerable reduction in the complexity of the requested theoretical
treatments for simple and complex geometries, e.g. in the case of problems
without heat transfer the energy equation does not have to be solved.
3.2 Molecular Properties and Quantities of Continuum Mechanics 51
The simplified basic equations of fluid mechanics, derived for incompress-
ible media, can occasionally also be applied to flows of compressible fluids,
such for cases where the density variations, occurring in the entire flow field,
are small compared with the fluid density. This point is treated separately in
Chap. 12, where conditions are derived under which density changes in gases
can be neglected for the treatment of flow processes. Flows in gases can be
treated like incompressible flows under the conditions indicated there.
For further characterization of a fluid, reference is made to the well-known
fact that solids conserve their form, whereas a fluid volume has no form of its
own, but takes the form of the container in which it is kept. Liquids differ from
gases in terms of the available volume taken by the fluids, filling only part
of the container, whereas the remaining part is either not filled or contains a
gas and there exists a free surface between liquid and the gas. Such a surface
does not exist when the container is filled only with a gas. As already said,
a gas takes up the entire container volume.
Finally, it can be concluded that there are a number of media that can only
be categorized, in a limited way, according to the above classification. They
include media that consist of two-phase mixtures. These have properties that
cannot be classified so easily. This holds also for a number of other media
that can, as per the above classification, be assigned neither to solids nor
to fluids and they start to flow only above a certain value of their internal
“shear stress”. Media of this kind will be excluded from this book, so that the
above-indicated classifications of media into solids and fluids remain valid.
Further restrictions on the fluid properties, that are applied in dealing with
flow problems in this book, are clearly indicated in the respective sections. In
this way, it should be possible to avoid mistakes that often arise in derivations
of fluid mechanics equations valid only for simplified fluid properties.
3.2 Molecular Properties and Quantities
of Continuum Mechanics
As all matter consists of molecules or aggregations of molecules, all macro-
scopic properties of matter can be described by molecular properties. Hence
it is possible to derive all properties of fluids that are of importance for con-
siderations in fluid mechanics, from properties of molecules, i.e. macroscopic
properties of fluids can be described by molecular properties. However, a
molecular description of the state of matter requires much effort owing to
the necessary extensive formalism and moreover the treatment of macro-
scopic properties would remain unclear. A molecular-theoretical treatment of
fluid properties would hardly be appropriate to supply application-oriented
fluid mechanics information in an easily comprehensible form. For this rea-
son, it is more advantageous to introduce quantities of continuum mechanics
for describing fluid properties. The connection between continuum mechanics
52 3 Physical Basics
quantities, introduced in fluid mechanics, and the molecular properties should
be considered, however, as the most important links between the two differ-
ent ways of description and presentation of fluid properties. Every student
should have a firm knowledge regarding this kind of considerations.
Some properties of the thermodynamic state of a fluid, such as density ρ,
pressure P and temperature T , are essential for the description of fluid me-
chanics processes and these can easily be expressed in terms of molecular
quantities. From the following derivations one can infer that the effects of
molecules or molecular properties on fluid elements or control volumes are
taken into consideration by introducing the properties the density ρ,pres-
sure P , temperature T ,viscosityµ, etc., in an “integral form”. As will be
seen, this integral consideration is sufficient for fluid mechanics. Therefore,
continuum mechanics considerations do not neglect the molecular structure
of the fluids, but take molecular properties into account in an integral form,
i.e. averaged over a high number of molecules.
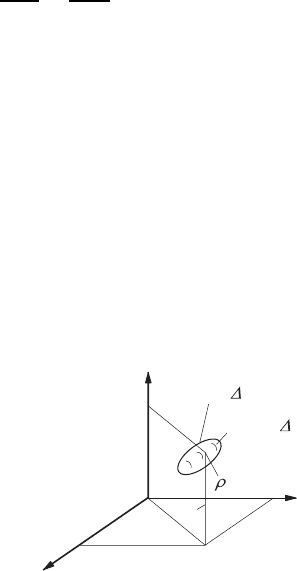
The mass per unit volume is called the specific density ρ of a material.
For a fluid element this quantity depends on its position in space, i.e. on
x
i
=(x
1
,x
2
,x
3
), and also on time t, so that generally
ρ(x
i
,t) = lim
∆V →δV
∆M
∆V
=
δm
δV
(3.1)
holds (Figs. 3.1 and 3.2). If n is considered to be the mean number of the
molecules existing per unit volume and m the mass of a single molecule, the
following connection between ρ, n and m holds:
ρ(x
i
,t)=mn(x
i
,t). (3.2)
The density of the matter is thus identical with the number of molecules
available per unit volume, multiplied by the mass of a single molecule. There-
fore, changes of density in space and in time correspond to spatial and
temporal changes of the mean number of molecules available per unit volume,
i.e. where ρ is large, n is large.
Fig. 3.1 Definition of the fluid density at a
point in space, ρ(x
i
,t)
Mass
M
Volume
V
x
1
x
2
x
1
x
2
x
3
x
3
(
x
i
,t
)

3.2 Molecular Properties and Quantities of Continuum Mechanics 53
Fig. 3.2 Fluctuations with increas-
ing ∆V while determining the den-
sity of fluids
Stochastic considerations of the thermal molecular motions in a fluid
volume permit, having a very large number of molecules under normal con-
ditions, a mean number of molecules to be specified at time t. Volumes of the
order of magnitude of 10
−18
–10
−20
m
3
are considered to be sufficiently large
for arriving at a clear definition of density for gases. The treatments of flow
processes in fluid mechanics are usually carried out for much larger volumes,
therefore the specification of a “mean number of molecules” is appropriate in
order to provide the needed mass in the considered volume. The local den-
sity ρ(x
i
,t) therefore describes a property of matter that is essential for fluid
mechanics with a precision that is sufficient to treat fluid flows. The control
volumes in fluid mechanics considerations are always selected such that the
determination of a local density value is possible in spite of the molecular
nature of matter. Its said above, a volume size of 10
−18
–10
−20
m
3
fulfills the
requirements of the considerations that are to be carried out from the fluid
mechanics point of view. Hence, as said above, ρ canbedefinedinspiteof
the molecular structure of the fluids considered.
Similar considerations can also be made for the pressure that occurs in a
fluid at rest and which is defined as the force acting per unit area (Figs. 3.3
and 3.4), i.e.:
P (x
i
,t)=− lim
∆F
j
→δF
j
∆K
j
∆F
j
(3.3)
From the point of view of molecular theory, the pressure effect is defined as
the momentum change per unit time felt per unit area, i.e. the force which
the molecules experience and exert on a wall when colliding in an elastic
way with the wall in the considered area. The following relation holds (see
Sect. 3.3.2):
P =
1
3
mn
u
2
=
1
3
ρ
u
2
, (3.4)
where m is the molecular mass, n the number of the molecules per unit
volume and mean u the thermal velocity of the molecules.
Analogous to the above volume dimensions, it can be stated that most
fluid mechanics considerations do not require area resolutions that fall below
