Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows
Подождите немного. Документ загружается.

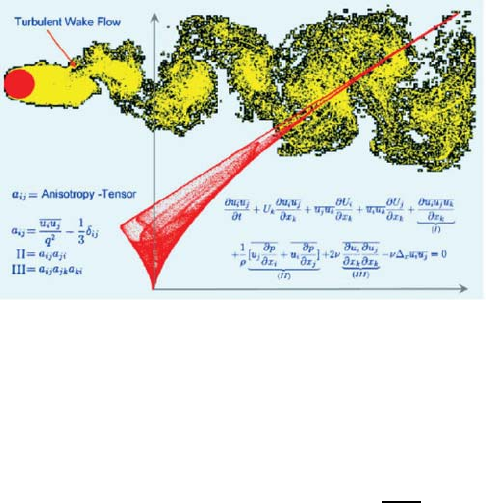
14 1 Introduction, Importance and Development of Fluid Mechanics
Fig. 1.8 Diagram of the turbulence anisotropy due to the invariants of the anisotropy
tensor
problems numerically. Numerical fluid mechanics has therefore also become
an important sub-domain of the entire field of fluid mechanics. Its significance
will increase further in the future.
One can expect in particular new ans¨atze in the development of turbu-
lence models which will use invariants of the tensors
u
i
u
j
,
ij
, etc., so that
the limitations of modelling turbulent properties of flows can be taken into
consideration. This is indicated in Fig. 1.8. Information of this kind can be
used for advanced turbulence modeling.
References
1.1. Bell ET (1936) Men of Mathematics. Simon & Schuster, New York
1.2. Rouse H (1952) Present day trends in hydraulics. Applied Mechanics Reviews
5:2
1.3. Bateman H, Dryden HL, Murnaghan FP (1956) Hydrodynamics. Dover, New
York
1.4. Van Dyke M (1964) Perturbation Methods in Fluid Mechanics. Academic press,
New York
1.5. Rouse H, Ince S (1980) History of Hydraulics. The University of Iowa, Institute
of Hydraulic Research, Ames, IA
1.6. Sˇzabo I (1987) Geschichte der mechanischen Prinzipien und ihrer wichtigsten
Anwendungen. Birkhaeuser, Basel
Chapter 2
Mathematical Basics
2.1 Introduction and Definitions
Fluid mechanics deals with transport processes, especially with the flow- and
molecule-dependent momentum transports in fluids. Their thermodynamic
properties of state such as pressure, density, temperature and internal energy
enter into fluid mechanics considerations. The thermodynamic properties of
state of a fluid are scalars and as such can be introduced into the equa-
tions for the mathematical description of fluid flows. However, in addition to
scalars, other kinds of quantities are also required for the description of fluid
flows. In the following sections it will be shown that fluid mechanics consid-
erations result in conservation equations for mass, momentum, energy and
chemical species which comprise scalar, vector and other tensor quantities.
Often fundamental differentiations are made between such quantities, with-
out considering that the quantities can all be described as tensors of different
orders. Hence one can write:
Scalar quantities = tensors of zero order ; {a}→a
Vectorial quantities = tensors of first order ; {a
i
}→a
i
Tensorial quantities = tensors of second order ; {a
ij
}→a
ij
where the number of the chosen indices i, j, k, l, m, n of the tensor presenta-
tion designates the order and ‘a’ can be any quantity under consideration. The
introduction of tensorial quantities, as indicated above, permits extensions
of the description of fluid flows by means of still more complex quantities,
such as tensors of third or even higher order, if this becomes necessary for
the description of fluid mechanics phenomena. This possibility of extension
and the above-mentioned standard descriptions led us to choose the indicated
tensor notation of physical quantities in this book, the number of the indices
i, j, k, l, m, n deciding the order of a considered tensor.
Tensors of arbitrary order are mathematical quantities, describing physical
properties of fluids, with which “mathematical operations” such as addition,
15

16 2 Mathematical Basics
subtraction, multiplication and division can be carried out. These may be
well known to many readers of this book, but are presented again below as
a summary. Where the brevity of the description does not make it possible
for readers, not accustomed to tensor descriptions, to familiarize themselves
with the matter, reference is made to the corresponding mathematical liter-
ature; see Sect. 2.12. Many of the following deductions and descriptions can,
however, be considered as simple and basic knowledge of mathematics and it
is not necessary that the details of the complete tensor calculus are known.
In the present book, only the tensor notation is used, along with simple parts
of the tensor calculus. This will become clear from the following explana-
tions. There are a number of books available that deal with the matter in the
sections to come in a mathematical way, e.g. see refs. [2.1] to [2.7].
2.2 Tensors of Zero Order (Scalars)
Scalars are employed for the description of the thermodynamic state vari-
ables of fluids such as pressure, density, temperature and internal energy, or
they describe other physical properties that can be given clearly by stating
an amount of the quantity and a dimensional unit. The following examples
explain this:
P =7.53 × 10
6
Amount
N
m
2
Unit
,T= 893.2
Amount
K
Unit
,ρ=1.5 × 10
3
Amount
kg
m
3
Unit
(2.1)
Physical quantities that have the same dimension can be added and sub-
tracted, the amounts being included in the adding and subtracting operations,
with the common dimension being maintained:
N
α=1
a
α
=
N
α=1
|a
α
|
Amount
a
Unit
a±b =(|a|±|b|)
Amount
a or b
Unit
, with
a
=
b
(2.2)
Quantities with differing dimensions cannot be added or subtracted.
The mathematical laws below can be applied to the permitted additions
and subtractions of scalars, see for details [2.5] and [2.6].
The amount of ‘a’isarealnumber,i.e.|a| is a real number if a ∈ R.Itis
defined by |a| := +a, if a ≥ 0and|a| := −a, if a<0.
The following mathematical rules can be deducted directly from this
definition:
−|a|≤a ≤|a|, |−a| = |a|, |ab| = |a||b|,
a
b
=
|a|
|b|
(if b =0)
|a|≤b ⇔−b ≤ a ≤ b
2.3 Tensors of First Order (Vectors) 17
From −|a|≤a ≤|a| and −|b|≤b ≤|b|, it follows that −(|a| + |b|) ≤
a + b ≤ (|a|+ |b|) . Thus for all a, b ∈ R:
|a + b|≤|a| + |b| (triangular inequality)
The commutative and associative laws of addition and multiplication of
scalar quantities are generally known and need not be dealt with here any
further. If one carries out multiplications or divisions with scalar physical
quantities, new physical quantities are created. These are again scalars, with
amounts that result from the multiplication or division of the corresponding
amounts of the initial quantities. The dimension of the new scalar physical
quantities results from the multiplication or division of the basic units of the
scalar quantities:
a · b =(|a|·|b|)
Amount
[a] · [b]
Unit
and
a
b
=
|a|
|b|
Amount
·
[a]
[b]
Unit
(2.3)
It can be seen from the example of the product of the pressure P and the
volume V how a new physical quantity results:
P · V = |P |·|V |
N
m
2
· m
3
[J=N m]
= |P |·|V |
Nm
(2.4)
The new physical quantity has the unit J = joule, i.e. the unit of energy. When
a pressure loss ∆P is multiplied with the volumetric flow rate, a power loss
results:
∆P ·
˙
V = |∆P ||
˙
V |
N
m
2
·
m
3
s
= |∆P ||
˙
V |
Nm
s
[W=
Nm
s
]
(2.5)
The power loss has the unit W = watt = joule/s.
2.3 Tensors of First Order (Vectors)
The complete presentation of a vectorial quantity requires the amount of the
quantity to be given, in addition to its direction and its unit. Force, velocity,
momentum, angular momentum, etc., are examples for vectorial quantities.
Graphically, vectors are represented by arrows, whose length indicates the
amount and the position of the arrow origin and the arrowhead indicates the
direction. The derivable analytical description of vectorial quantities makes
use of the indication of a vector component projected on to the axis of a
coordinate system, and the indication of the direction is shown by the signs
of the resulting vector components.
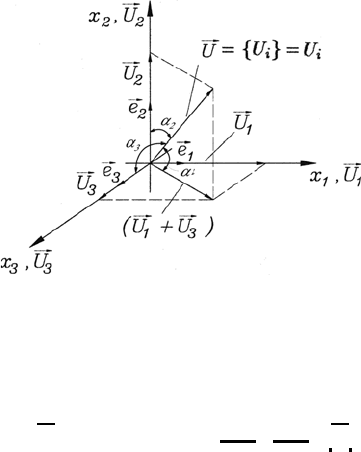
18 2 Mathematical Basics
Fig. 2.1 Representation of velo-
city vector U
i
in a Cartesian
coordinate system
To represent the velocity vector {U
i
}, for example, in a Cartesian coordi-
nate system, the components U
i
(i =1, 2, 3) can be expressed as follows:
U = {U
i
} =
⎧
⎨
⎩
U
1
U
2
U
3
⎫
⎬
⎭
= |U|
⎧
⎨
⎩
cos α
1
cos α
2
cos α
3
⎫
⎬
⎭
m
s
; U
i
= ±
Direction
|U|·|cos α
i
|
Amount
m
s
Unit
(2.6)
Looking at Fig. 2.1, one can see that the following holds:
U
1
= U
1
· e
1
, U
2
= U
2
· e
2
, U
3
= U
3
· e
3
(2.7)
where the unit vectors e
1
, e
2
, e
3
in the coordinate directions x
1
,x
2
and x
3
are employed. This is shown in Fig. 2.1. α
i
designates the angle between U
and the unit vector e
i
. Vectors can also be represented in other coordinate
systems; through this, the vector does not change in itself but its mathemat-
ical representation changes. In this book, Cartesian coordinates are preferred
for presenting vector quantities.
Vector quantities which have the same unit can be added or subtracted
vectorially. Laws are applied here that result in addition or subtraction of
the components on the axes of a Cartesian coordinate system:
a ± b = {a
i
}±{b
i
} = {(a
i
± b
i
)} = {(a
1
± b
1
), (a
2
± b
2
), (a
3
± b
3
)}
T
Vectorial quantities with different units cannot be added or subtracted
vectorially. For the addition and subtraction of vectorial constants (having
the same units), the following rules of addition hold:
a + 0 = {a
i
} + {0} = a (zero vector or neutral element 0)
a +(−a)={a
i
} + {−a
i
} = 0 (a element inverse to −a)
a + b = b + a, d.h. {a
i
} + {b
i
} = {b
i
} + {a
i
}
= {(a
i
+ b
i
)} (commutative law)
a +(b + c)=(a + b)+c, d.h. {a
i
} + {(b
i
+ c
i
)}
= {(a
i
+ b
i
)} + {c
i
} (associative law)

2.3 Tensors of First Order (Vectors) 19
With (α · a) a multiple of a results, if α>0. α has no unit of its own, i.e.
(α ·a) designates the vector that has the same direction as a but has α times
the amount. In the case α<0, one puts (α · a):=−(|α|·a). For α =0the
zero vector results: 0 · a = 0.
When multiplying two vectors two possibilities should be distinguished
yielding different results.
The scalar product a · b of the vectors a and b is defined as
a · b :=
|a|·|b|·cos(a, b), if a = 0 and b = 0
0, if a = 0 or b = 0
(2.8)
where the following mathematical rules hold:
a · b = b · aa· b =
−
→
0 ⇔ if a orthogonal to b
(αa) · b = a · (αb)=α(a · b) |a|
def
=
√
a · a
(a + b) · c = a · c + b · c
(2.9)
When the vectors a and b are represented in a Cartesian coordinate system,
the following simple rules arise for the scalar product (a ·b)andforcos(a, b):
a · b = a
1
b
1
+ a
2
b
2
+ a
3
b
3
, |a| =
a
2
1
+ a
2
2
+ a
2
3
(2.10)
cos(a, b)=
a · b
|a||b|
=
a
1
b
1
+ a
2
b
2
+ a
3
b
3
a
2
1
+ a
2
2
+ a
2
3
b
2
1
+ b
2
2
+ b
2
3
(2.11)
The above equations hold for a, b =
−→
0 . Especially the directional cosines in
a Cartesian coordinate system are calculated as
cos(a, e
i
)=
|a
i
|
a
2
1
+ a
2
2
+ a
2
3
i =1, 2, 3 (2.12)
i.e. a
i
represents the angles between the vector a and the base vectors
e
1
=
⎧
⎨
⎩
1
0
0
⎫
⎬
⎭
, e
2
=
⎧
⎨
⎩
0
1
0
⎫
⎬
⎭
, e
3
=
⎧
⎨
⎩
0
0
1
⎫
⎬
⎭
(2.13)
The vector product a × b of the vectors a and b has the following
properties:
a × b is a vector = 0,ifa = 0 and b = 0 and a is not parallel to b;
|a × b| = |a|·|b|sin(a, b) (area of the parallelogram set up by a and b);
a×b is a vector standing perpendicular to a and b and can be represented
with (a, b, a × b), a right-handed system.
It can easily be seen that a ×b = 0,ifa = 0 or b = 0 or a is parallel to b.
One should take into consideration that for the vector product the associative
law does not hold in general:
a ×
(b × c) =(a × b) × c

20 2 Mathematical Basics
Fig. 2.2 Graphical representation of a vector
product a × b
The following computation rules can be stated (Fig. 2.2):
a × a =0, a × b = −(b × a),
α(a × b)=(αa) × b = a × (αb)(forα ∈ R)
a × (b + c)=a × b + a × c
(a + b) × c = a × c + b × c (distributive laws)
a × b =0 ⇔ a =0orb =0ora, b parallel (parallelism test)
|a × b|
2
= |a|
2
·|b|
2
− (a ·b)
2
If one represents the vectors a and b in a Cartesian coordinate system with
e
i
, the following computation rule results:
⎧
⎨
⎩
a
1
a
2
a
3
⎫
⎬
⎭
×
⎧
⎨
⎩
b
1
b
2
b
3
⎫
⎬
⎭
=
e
1
a
1
b
1
e
2
a
2
b
2
e
3
a
3
b
3
=
⎧
⎨
⎩
a
2
b
3
− a
3
b
2
a
3
b
1
− a
1
b
3
a
1
b
2
− a
2
b
1
⎫
⎬
⎭
(2.14)
The tensor of third order
ijk
:= e
i
· (e
j
× e
k
) that will be introduced in
Sect. 2.5 permits, moreover, a computation of a vector product according to
{a
i
}×{b
j
} :=
ijk
a
i
b
j
(2.15)
A combination of the scalar product and the vector product leads to the
scalar triple product (STP) formed of three vectors:
a, b, c
= a · (b × c) (2.16)
The properties of this product from three vectors can be seen from Fig. 2.3.
The STP of the vectors a, b, c leads to six times the volume of the parallelo-
piped (ppd), V
ppd
, defined by the vectors: a, b and c.
The “parallelopiped product” of the three vectors a, b, c is calculated from
the value of a triple-row determinant:
[a, b, c]=
a
1
b
1
c
1
a
2
b
2
c
2
a
3
b
3
c
3
(2.17)

2.4 Tensors of Second Order 21
Fig. 2.3 Graphical representation of scalar triple product by three vectors
V
ppd
=
1
6
V
STP
=
1
6
[a, b, c] (2.18)
It is easy to show that for the STP
a · (b × c)=b · (a × c)=c · (a × b)
− b · (a × c) (2.19)
For the vector triple product a × b × c, the following relation holds:
a × (b × c)=(a ·c)b − (a · b)c (2.20)
Further important references are given in books on vector analysis; see also
Sect. 2.12.
2.4 Tensors of Second Order
In the preceding two sections, tensors of zero order (scalar quantities) and
tensors of first order (vectorial quantities) were introduced. In this section, a
summary concerning tensors of second order is given, which can be formulated
as matrices with nine elements:
{a
ij
} =
⎧
⎨
⎩
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
⎫
⎬
⎭
= a
ij
(2.21)
In the matrix element a
ij
, the index i represents the number of the row and j
represents the number of the column, and the elements designated with i = j
are referred to as the diagonal elements of the matrix. A tensor of second
order is called symmetrical when a
ij
= a
ji
holds. The unit second-order
tensor is expressed by the Kronecker delta:
δ
ij
=
⎧
⎨
⎩
100
010
001
⎫
⎬
⎭
, i.e. δ
ij
=
+1 if i = j
0ifi = j
(2.22)
22 2 Mathematical Basics
The transposed tensor of {a
ij
} is formed by exchanging the rows and
columns of the tensor: {a
ij
}
T
= {a
ji
}. When doing so, it is apparent that the
transposed unit tensor of second order is again the unit tensor, i.e. δ
T
ij
= δ
ij
.
The sum or difference of two tensors of second order is defined as a tensor
of second order whose elements are formed from the sum or difference of the
corresponding ij elements of the initial tensors:
{a
ij
± b
ij
} =
⎧
⎨
⎩
a
11
± b
11
a
12
± b
12
a
13
± b
13
a
21
± b
21
a
22
± b
22
a
23
± b
23
a
31
± b
31
a
32
± b
32
a
33
± b
33
⎫
⎬
⎭
(2.23)
In the case of the following presentation of tensor products, often the so-
called Einstein’s summation convention is applied. By this one understands
the summation over the same indices in a product.
When forming a product from tensors, one distinguishes the outer prod-
uct and the inner product. The outer product is again a tensor, where each
element of the first tensor multiplied with each element of the second tensor
results in an element of the new tensor. Thus the product of a scalar and a
tensor of second order forms a tensor of second order, where each element
results from the initial tensor of second order by scalar multiplication:
α ·{a
ij
} = {α · a
ij
} =
⎧
⎨
⎩
α · a
11
α · a
12
α · a
13
α · a
21
α · a
22
α · a
23
α · a
31
α · a
32
α · a
33
⎫
⎬
⎭
(2.24)
The outer product of a vector (tensor of first order) and a tensor of second
order results in a tensor of third order with altogether 27 elements. The
inner product of tensors, however, can result in a contraction of the order.
As examples are cited the products a
ij
· b
j
:
{a
ij
}·{b
j
} =
⎧
⎨
⎩
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
⎫
⎬
⎭
⎧
⎨
⎩
b
1
b
2
b
3
⎫
⎬
⎭
=
⎧
⎨
⎩
a
11
b
1
+ a
12
b
2
+ a
13
b
3
a
21
b
1
+ a
22
b
2
+ a
23
b
3
a
31
b
1
+ a
32
b
2
+ a
33
b
3
⎫
⎬
⎭
(2.25)
and
{b
i
}
T
·{a
ij
} = {b
1
,b
2
,b
3
}·
⎧
⎨
⎩
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
⎫
⎬
⎭
=
⎧
⎨
⎩
b
1
a
11
+ b
2
a
21
+ b
3
a
31
b
1
a
12
+ b
2
a
22
+ b
3
a
32
b
1
a
13
+ b
2
a
23
+ b
3
a
33
⎫
⎬
⎭
T
(2.26)
In summary, this can be written as
{a
ij
}·{b
j
} = {(a
ij
b
j
)} = {(ab)
i
} (2.27)
and
{b
i
}·{a
ij
} = {(b
i
a
ij
)} = {(ab)
j
} (2.28)
2.5 Field Variables and Mathematical Operations 23
If one takes into account the above product laws:
{δ
ij
}·{b
j
} = {b
i
} and {b
i
}
T
·{δ
ij
} = {b
j
}
T
(2.29)
The multiplication of a tensor of second order by the unit tensor of second
order, i.e. the “Kronecker delta”, yields the initial tensor of second order:
{δ
ij
}·{a
ij
} =
⎧
⎨
⎩
100
010
001
⎫
⎬
⎭
·
⎧
⎨
⎩
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
⎫
⎬
⎭
= {a
ij
} (2.30)
Further products can be formulated, as for example cross products between
vectors and tensors of second order:
{a
i
}·{b
jk
} =
ikj
· a
i
· b
jk
(2.31)
but these are not of special importance for the derivations of the basic laws
in fluid mechanics.
2.5 Field Variables and Mathematical Operations
In fluid mechanics, it is usual to present thermodynamic state quanti-
ties of fluids, such as density ρ, pressure P , temperature T and internal
energy e, as a function of space and time, a Cartesian coordinate system
being applied here generally. To each point P(x
1
,x
2
,x
3
)=P(x
i
)avalue
ρ(x
i
,t),P(x
i
,t),T(x
i
,t),e(x
i
,t), etc., is assigned, i.e. the entire fluid proper-
ties are presented as field variables and are thus functions of space and time
Fig. 2.4. It is assumed that in each point in space the thermodynamic connec-
tions between the state quantities hold, as for example the state equations
that can be formulated for thermodynamically ideal fluids as follows:
ρ = constant (state equation of the thermodynamically ideal liquids)
P/ρ = RT (state equation of the thermodynamically ideal gases)
Entirely analogous to this, the properties of the flows can be described by
introducing the velocity vector, i.e. its components, as functions of space and
time, i.e. as vector field Fig. 2.5. Furthermore, the local rotation of the flow
field can be included as a field quantity, as well as the mass forces and mass
acceleration acting locally on the fluid. Thus the velocity U
j
= U
j
(x
i
,t), the
rotation ω
j
= ω
j
(x
i
,t), the force K
j
= K
j
(x
i
,t) and the acceleration g
j
(x
i
,t)
canbestatedasfieldquantitiesandcanbeemployedassuchquantitiesin
the following considerations.
In an analogous manner, tensors of second and higher order can also be
introduced as field variables, for example, τ
ij
(x
i
,t), which is the molecule-
dependent momentum transport existing at a point in space, i.e. at the point
