Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

34 2 Mathematical Basics

If one considers two inﬁnitesimal closely neighbouring points P



)

and P



+dx



+dx



+dx



), for the diﬀerence of their position

vectors r

= r(x



)andr

= r(x



+dx



+dx



+dx



)atthe

lowest order (Taylor expansion)

dr = r

− r



i=1

∂r

∂x



(2.85)

holds. The length of the distance vector dr, the so-called line element ds,

when employing the deﬁnition for the metric coeﬃcients, is given by

=dr



i=1

(2.86)

A vector ﬁeld f is represented by its components in curvilinear coordinate

systems:

f = f

+ f

(2.87)

Without derivation, the following relationships for diﬀerential operators are

stated in curvilinear orthogonal coordinates:

• Surface elements:

dS =

∂r

∂x



∂r

∂x



,i= j =1, 2, 3 (2.88)

• Volume elements:

dV = h



(2.89)

• Gradient of a scalar ﬁeld Φ:

grad Φ = ∇Φ =



i=1

∂Φ

∂x



(2.90)

• Divergence:

div f = ∇·f =



∂h

∂x



∂h

∂x



∂h

∂x





(2.91)

• Rotation:

rot f = ∇×f =



∂

∂x



∂

∂x



∂

∂x





(2.92)

• Laplace operator:

∆Φ = ∇·∇Φ = div grad Φ =



∂

∂x





∂Φ

∂x





∂

∂x





∂Φ

∂x





∂

∂x





∂Φ

∂x





(2.93)

2.10 Diﬀerential Operators in Curvilinear Orthogonal Coordinates 35

When employing diﬀerential operators in curvilinear coordinates, the depen-

dence of the (local) unit vectors and metric coeﬃcients of the coordinates is

also to be taken into account at least in principle.

Example 1: Cylindrical Coordinates (r, ϕ, z) (Fig. 2.6)

• Conversion in Cartesian coordinates:

x = r cos ϕ

y = r sin ϕ (2.94)

z = z

(0 ≤ r<∞, 0 ≤ ϕ ≤ 2π, −∞ <z<∞)

• Position vector:

r = x(r, ϕ, z)e

+ y(r, ϕ, z)e

+ z(r, ϕ, z)e

= rr

(ϕ)+ze

(2.95)

• Local unit vectors:

=cosϕ e

+sinϕ e

= −sin ϕ e

+cosϕ e

(2.96)

= e

• Metric coeﬃcients or scaling factors:

=1,h

= r, h

= 1 (2.97)

• Gradient:

grad Φ =

∂Φ

∂r

∂Φ

∂ϕ

∂Φ

∂z

(2.98)

Fig. 2.6 Cylindrical coordinates

36 2 Mathematical Basics

Fig. 2.7 Spherical coordinates

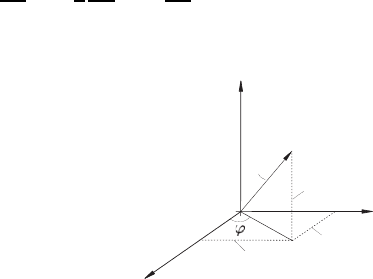
Example 2: Spherical Coordinates (r, θ, φ) (Fig. 2.7)

• Conversion in Cartesian coordinates:

x = r sin θ cos φ

y = r sin θ sin φ (2.99)

z = r cos θ

(0 ≤ r<∞, 0 ≤ θ ≤ π, 0 ≤ φ ≤ 2π)

• Metric coeﬃcients or scaling factors:

=1,h

= r, h

= r sin θ (2.100)

2.11 Complex Numbers

The introduction of complex numbers permits the generalization of basic

mathematical operations, as for example the square rooting of numbers, so

that the extended grouping of numbers can be stated as follows:

Complex numbers

Real numbers

Rational numbers

Integer numbers

Positive integer numbers

(Natural numbers)

Imaginary numbers

Irrational numbers

Fractional numbers

Negative integer numbers

Zero

By extending to complex functions, mathematically interesting descriptions

of technical problems become possible, for example the entire ﬁeld of potential

2.11 Complex Numbers 37

ﬂows; see Chap. 10. Complex numbers and complex functions therefore have

an important role in the ﬁeld of ﬂuid mechanics. As will be shown, potential

ﬂows can be dealt with very easily through functions of complex numbers.

It is therefore important to provide here an introduction to the theory of

complex numbers in a summarized way.

2.11.1 Axiomatic Introduction to Complex Numbers

A complex number can formally be introduced as an arranged pair of real

numbers (a, b) where the equality of two complex numbers z

=(a, b)and

=(c, d)isdeﬁnedasfollows:

Equality: z

=(a, b)=(c, d)=z

holds exactly when a = c and b = d

holds, where a, b, c, d ∈ R.

The ﬁrst component of a pair (a, b) is named the real part and the second

component the imaginary part.

For b =0,z =(a, 0) is obtained, with the real number a,sothatall

the real numbers are a sub-set of the complex numbers. When determining

basic arithmetics operations, one has to keep in mind that operations with

complex numbers lead to the same results as in the case of arithmetics of real

numbers, provided that the operations are restricted to real numbers in the

above sense, i.e. z =(a, 0).

Additions and multiplications of complex numbers are introduced by the

following relationships:

Addition: (a, b)+(c, d)=(a + c, b + d)

Multiplication: (a, b) · (c, d)=(ac − bd, ad + bc)

(2.101)

Then,

(a, 0) + (c, 0) = (a + c, 0) = a + c

(a, 0) · (c, 0) = (ac, 0) = ac

(2.102)

i.e. no contradictions to the computational rules with real numbers arise. The

quantity of the complex numbers (denoted C in the following) is complete as

far as addition and multiplication are concerned, i.e. with z

∈ C follows:

= z

+ z

∈ C

= z

· z

∈ C

(2.103)

Furthermore, it can be shown that the above operations of addition and

multiplication satisfy the following laws:

Commutative concerning addition: z

+ z

= z

+ z

Commutative concerning multiplication: z

= z

38 2 Mathematical Basics

Associative concerning additon: (z

+ z

)+z

= z

+(z

+ z

)

Associative concerning multiplicaton: (z

= z

)

Distributive properties: (z

+ z

= z

+ z

Analogous to the case of the real number z(a, 0), a so-called purely imaginary

number can also be introduced: z =0,b.

A complex number z =(a, b) is called imaginary if a =0andb =0.

Moreover, one puts i =(0, 1) and calls i an imaginary unit.

According to the multiplication rules, introduced for complex numbers,

this complex number i, i.e. the number pair (0, 1), has a special role, namely,

=(0, 1) · (0, 1) = (−1, 0) = −1 (2.104)

i.e. the multiplication of the imaginary unit number by itself yields the real

number −1. Based on equation (2.103), it can be represented as

i =

√

−1 (2.105)

where the unambiguity of the root relationship for i requires some special

considerations. Because

z =(a, b)=(a, 0) + (0,b)=(a, 0) + (0, 1) · (b, 0) = a + ib (2.106)

each complex number z =(a, b) can also be written as the sum of a real

number a and an imaginary number ib.

Subtraction and division can be achieved by inversion of the addition and

multiplication, i.e., (z

− z

) is equal to the complex number z

,forwhich

+ z

= z

(2.107)

holds. Following the above notation with z

=(a, b), z

=(c, d)resultsin

− z

=(a − c, b − d) (2.108)



ac + bd

+ d

)

bc − ad

+ d

)



(2.109)

In the above presentations, elementary mathematical operations based on the

quantity C of the complex numbers were introduced. All other properties of

the complex numbers are followed in the implementation of these deﬁnitions.

2.11.2 Graphical Representation of Complex Numbers

In order to explain the above properties of complex numbers, they are often

shown graphically in ways summarized below. Several kinds of presentations

are chosen in the literature for a better understanding.

2.11 Complex Numbers 39

Fig. 2.8 Diagram of a complex number in the

Gauss number plane

z=x+iy

Every point z in

the plane represents

a complex number

2.11.3 The Gauss Complex Number Plane

As the complex number z = x + iy represents an arranged pair of numbers, a

rectangular coordinate system is recommended for the graphical representa-

tion of complex numbers, in which a real axis for x and an “imaginary axis”

for iy is deﬁned. The complex number z = x + iy is then deﬁned as a point

in this plane, or as a vector z from the origin of the coordinate system to the

point Z with the coordinates (x, iy). This is illustrated in Fig. 2.9, where the

addition and subtraction of complex numbers are stated graphically.

2.11.4 Trigonometric Representation

If one considers the graphical representation in Fig. 2.8, the following trigono-

metric relations can be given for complex numbers:

x = r cos ϕ and y = r sin ϕ with r = | z | (2.110)

A complex number can therefore be written as follows:

z = r cos ϕ + i(r sin ϕ)=r(cos ϕ + i sin ϕ) (2.111)

z = re

iϕ

(2.112)

The connection between the exponential function and the trigonometric func-

tions follows immediately by a series expansion of the exponential function

and rearrangement of the series, i.e.

iϕ

∞



k=0

(iϕ)

∞



k=0

(−1)

(2k)!

+ i

∞



k=0

(−1)

2k+1

(2k +1)!

=cosϕ + i sin ϕ

(2.113)

40 2 Mathematical Basics

Fig. 2.9 Diagram of the addition and subtrac-

tion of complex numbers in the Gauss number

plane

Fig. 2.10 Graphical representation of multipli-

cation of complex numbers

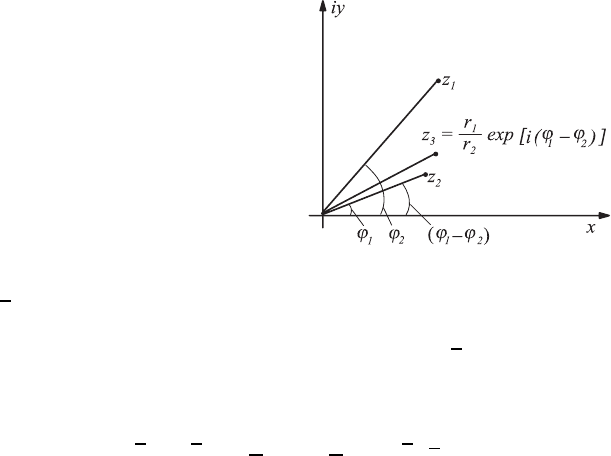
With the following relationship, the multiplication and division of complex

numbers can be carried out:

= r

i(ϕ

+ϕ

)

= r

(cos(ϕ

+ ϕ

)+i sin(ϕ

+ ϕ

)) (2.114)

i(ϕ

−ϕ

)

(cos(ϕ

− ϕ

)+i sin(ϕ

− ϕ

)) (2.115)

These multiplications and divisions of complex numbers can be represented

graphically as shown in Figs. 2.9 and 2.10.

At this point, it is advisable to discuss the treatment of the roots of com-

plex numbers. It is explained below, how the mathematical operator



() is

to be applied to a complex number.

It is agreed that

√

z (n ∈ N = (natural number)) is the set of all those

numbers raised to the 1/nth power of the number z. Therefore, if one puts

z = r(cos ϕ + i sin ϕ) (2.116)

Then

√

z =

√



cos

ϕ+2kπ

+ i sin

ϕ+2kπ



√

(

2kπ

)

k =0, 1, 2,...,n− 1

(2.117)

2.11 Complex Numbers 41

Fig. 2.11 Graphical representation of

division of complex numbers

i.e.

√

z is a set of complex numbers consisting of n numbersofvaluesthat

can be interpreted geometrically in the complex plane as corner points of a

polynomial, which is inscribed in a circle with radius

√

r around the zero

point.

Speciﬁcally for k = 0, for example:

√

z =

√



cos

+ i sin



√

(2.118)

2.11.5 Stereographic Projection

The above representations of complex numbers were described by using the

plane employed in the ﬁeld of analytical geometry and well known trigono-

metric relationships were used. For many purposes it proves more favorable

to understand the points in the x −iy plane as projections of points lying on

a unit sphere, whose poles lie on the axis perpendicular to the complex plane.

One of the poles of the sphere lies at the zero point, whereas the other takes

the position coordinates (0, 0, 1). Stereographic projections are carried out

from the latter pole as indicated in Fig. 2.12. Thus each point of the plane

corresponds precisely to a point of the sphere which is diﬀerent from N and

vice versa, i.e. the spherical surface is, apart from the starting point of the

projection, projected reversibly in an unequivocal manner on to the complex

plane. The ﬁgure is circle-allied and angle-preserving.

• The property of the circle-allied ﬁgure indicates that each circle on the

sphere is projected as a circle or a straight line on the plane (and vice

versa).

• The angle-preserving ﬁgure signiﬁes that two arbitrary circles (and gen-

erally any two curves on the sphere) intersect at the same angle as their

stereographic projection in the plane (and vice versa).

42 2 Mathematical Basics

Fig. 2.12 Representation of the stereographic projection (complex sphere of

Riemann)

2.11.6 Elementary Function

Complex functions are deﬁned analogously to the introduction of real func-

tions and can be given as follows:

When C is an arbitrary set of complex numbers, C can be designated as the

domain of the complex variables z. If one assigns to each complex variable z,

within the domain C, a complex quantity F(z), then F (z)isdesignatedasthe

function of complex variables. The function F(z) represents again a complex

quantity:

F (z)=Φ + iΨ (2.119)

Here it is to be considered in general that the quantities Φ and Ψ again depend

on x and iy, i.e. on the coordinates of the complex variable z.

When the deﬁnition of a complex function is compared with the often eas-

ier understandable real functions, the diﬀerentiation of a complex function

has a signiﬁcant diﬀerence compared to real functions. The existence of a

derivative f



(x) of a real function f (x) does not say anything about the

existence of possible higher-order derivatives, whereas from the existence

of ﬁrst-order derivative f



(x) of a complex function F (z), if automatically

follows the existence of all higher derivatives, i.e.

When a function F (z), in a ﬁeld G ∈ C is holomorphic (i.e. distinguishable in

a complex manner) and exists and if the function posseses F



(z), then there

exist all higher-order derivatives F



(z), F



(z),... also. Instead of the term

holomorphic, the term analytical is often used.

The representation of F (z) is often also treated as conformal mapping. The

reason for this is based on the fact that, under certain restrictive conditions,

the function F (z) assigned to each point P in the plane z can map into

another complex plane as a point Q in an imaginary plane W .Inorder

to achieve this unequivocal assignment, a branch of an equivocal function is

2.11 Complex Numbers 43

often introduced as the main branch and only the latter is used for computing.

The most important complex functions are as follows, see also refs. [2.2] and

[2.7].

Polynomials of nth Order

F (z)=a

+ a

z + a

+ ···+ a

(2.120)

where a

, a

, ..., a

are complex constants and n a positive total number.

The transformation F(z)=az + b is designated as a linear transformation

in general.

Rational Algebraic Function

F (z)=

P (z)

Q(z)

(2.121)

where P (z)andQ(z) are polynomials of arbitrary order. The special case

F (z)=

az + b

cz + d

(2.122)

where ad − bc = 0 is often designated as a fractional linear function.

Exponential Function

F (z)=e

=exp(z) (2.123)

where e =2.71828 ... represents the basis of the (real) natural logarithm.

Complex exponential functions have properties that are similar to those for

real exponential functions. For example:

· e

= e

)

(2.124)

= e

−z

)

(2.125)

Trigonometric Functions

The trigonometric functions for complex numbers are deﬁned as follows:

sin z =

− e

−iz

cos z =

+ e

−iz

(2.126)

sec z =

cos z

+ e

−iz

csc z =

sin z

− e

−iz

(2.127)

tan z =

sin z

cos z

− e

−iz

i(e

+ e

−iz

)

cot z =

cos z

sin z

i(e

+ e

−iz

)

− e

−iz

(2.128)