Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

196 7 Similarity Theory

Tab l e 7.1 Dimensions and units of important physical quantities of ﬂuid mechanics

Quantity, designation Dimensions Units

F,L,t,ϑ M,L,t,ϑ

Length LLmetre, m

Force FMLt

−2

newton, N

Mass FL

−1

M kilogram, kg

Time ttsecond, s

Temperature ΘΘkelvin, K

Velo city Lt

−1

Mass ﬂow ˙mFL

−1

tMt

−1

kg s

−1

Volume ﬂow L

−1

Pressure, stress FL

−2

−1

−2

pascal,

Pa = N m

−2

Work, energy FL ML

−2

joule,

J=Ws=Nm

Power FLt

−1

−3

watt,

W=Nms

−1

Density ρFL

−4

−3

kg m

−3

Dynamic viscosity µFL

−2

tML

−1

Pa s = N s m

−2

Kinematic viscosity νL

−1

Thermal expansion ϑ

−1

coeﬃcient β

Compressibility F

−1

−2

−1

coeﬃcient α

Speciﬁc heat capacity c

−2

−1

−2

−1

Jkg

−1

Thermal conductivity λFt

−1

MLt

−3

−1

Surface tension σFL

−1

−2

−1

Thermal L

−1

diﬀusivity a = λ/ρc

Heat transfer FL

−1

−3

−1

−2

−1

coeﬃcient α

Gas constant RL

−2

−1

−2

−1

Jkg

−1

Entropy sL

−2

−1

−2

−1

Jkg

−1

1. Similarity of molecular transport processes

Pr = ν/a =(µc

/λ) = Prandtl number

Sc = ν/D = µ/(ρD) = Schmidt number

2. Similarity of ﬂow processes

Re = LU/ν = Reynolds number

Fr = U

g/L = Froude number

Ma = U/c =Machnumber

Eu = ∆P/ρU

= Euler number

St = Lf/U = Strouhal number, f is the frequency

Gr = L

gβρ

∆T/µ

=Grashofnumber

3. Similarity of heat transfer processes

Pe = ReP r = UL/a = Peclet number

= U

∆T =Eckertnumber

7.2 Dimensionless Form of the Diﬀerential Equations 197

4. Similarity of integral quantities of heat and mass transfer

Nu = αL/λ = Nusselt number

Sh = βL/D = Sherwood number

where α is introduced as heat transfer coeﬃcient and β as mass transfer

coeﬃcient.

It is recommended to bear these groups in mind when in the following

sections similarity theory and its application in ﬂuid mechanics are treated.

7.2 Dimensionless Form of the Diﬀerential Equations

7.2.1 General Remarks

In Chap. 5 it was shown that ﬂuid mechanics is a ﬁeld whose physical basics

not only exist in complete form, but can also be formulated as a complete

set of partial diﬀerential equations. Closing the momentum and energy equa-

tions, molecular transport properties of ﬂuids were included, i.e. the molecular

structure of the ﬂuids was introduced with regard to its integral eﬀect on

momentum, heat and mass transport. This resulted in a set of transport

equations which are summarized below for Newtonian ﬂuids:

• Continuity equation:

∂ρ

∂t

∂(ρU

)

∂x

=0 (7.3)

• Momentum equations (j =1, 2, 3):



∂U

∂t

+ U

∂U

∂x



= −

∂P

∂x

∂

∂x





∂U

∂x

∂U

∂x



−

∂U

∂x



+ ρg

(7.4)

or for ρ = constant and µ = constant:



∂U

∂t

+ U

∂U

∂x



= −

∂P

∂x

+ µ

∂

∂x

+ ρg

(7.5)

• Energy equation for ρ = constant, µ = constant and λ = constant:

ρc



∂T

∂t

+ U

∂T

∂x



= λ

∂

∂x

+ µΦ

(7.6)

198 7 Similarity Theory

with



∂U

∂x





∂U

∂x





∂U

∂x





∂U

∂x

∂U

∂x





∂U

∂x

∂U

∂x





∂U

∂x

∂U

∂x



(7.7)

• State equations:

= RT (ideal gas) and ρ = constant (ideal liquid) (7.8)

Through the above set of partial diﬀerential equations there exist excel-

lent conditions for all ﬁelds of ﬂuid mechanics for applying similarity

considerations. Similarity considerations can be introduced into the diﬀer-

ential equations in many ways, depending on the problem and the solution

sought or on the solution path that one wants to take. This is explained in

Sects. 7.2.2–7.2.4, by way of examples, see also refs. [7.1] to [7.4].

Looking at the above set of partial diﬀerential equations, one ﬁnds that the

solution requires the speciﬁcation of initial and boundary conditions. In simi-

larity analysis, these boundary conditions must meet strict similarity require-

ments. Geometric similarity of boundaries is an important prerequisite for

similar solutions of the above diﬀerential equations. As further considerations

show, the continuity equation can be employed to formulate the conditions

as to how the characteristic temporal changes of ﬂow ﬁelds are to be coupled

with the characteristic dimensions of ﬂow geometries and characteristic ﬂuid

velocities, in order to deduce the conditions for the similarity of solutions of

the basic ﬂuid-mechanical equations. Through the momentum equations, for

all three velocity components, which are formulated as equations of the forces

acting on a ﬂuid element (per unit volume), strict statements can be made

on the requirements that have to exist for the dynamic similarity of ﬂows.

Moreover, dynamic similarity is a prerequisite for the existence of kinematic

similarity of ﬂow ﬁelds that is often necessary for transferring the insights on

structural observations in one ﬂow to another ﬂow.

Finally, it should be pointed out that with the above locally formulated

energy equation, all information is available to ensure that for heat transfer

problems the conditions for caloric similarity are given. This then is again

a prerequisite for the existence of thermal similarity. Employing also the

state equations, the conditions required to transfer the temperature ﬁeld of

a gas ﬂow to the temperature ﬁeld of a liquid ﬂow can then be derived.

All these possibilities, to extend a solution from a special ﬂow or tempera-

ture ﬁeld, through similarity considerations, into generally valid knowledge,

make similarity theory an important section of ﬂuid mechanics. The fol-

lowing considerations show how one uses the insights, gained by similarity

considerations, of the diﬀerential equations, in diﬀerent applications in ﬂuid

mechanics.

7.2 Dimensionless Form of the Diﬀerential Equations 199

7.2.2 Dimensionless Form of the Diﬀerential

Equations

The deliberations in Sect. 7.1 show that insights into the existence of similar-

ity could be obtained by forming ﬁxed relationships from momentum changes

per unit time and corresponding force eﬀects. From this result, one can ob-

tain dimensionless characteristic numbers that are employed as a basis for

the desired generalizations of certain insights into ﬂuid ﬂows. Such knowl-

edge can also be gained when transferring the partial diﬀerential equations

summarized in Sect. 7.2.1 from their dimensional into a dimensionless form.

For this purpose, one introduces “characteristic quantities” that are desig-

nated below with the subscript c. All quantities marked with asterisks (*)

are dimensionless.

= U

∗

; t = t

∗

; ρ = ρ

∗

; P = ∆P

∗

; τ

= τ

∗

;

= g

∗

; µ = µ

∗

;etc.

When one inserts the dimensionless quantities into the continuity equation

(7.3), one obtains:

∂ρ

∂t

∂(ρU

)

∂x

∂ρ

∗

∂t

∗

∂(ρ

∗

)

∂x

∗

=0 (7.9)

or resulting:



St = Strouhal number

∂ρ

∗

∂t

∗

∂(ρ

∗

)

∂x

∗

=0. (7.10)

The above derivations make it clear that similar solutions for ﬂow problems

can follow from the continuity equation only when the Strouhal numbers for

two ﬂow problems A and B, to which the continuity equation is applied, are

equal, i.e. when the following holds:









. (7.11)

Normalizing also the momentum equations in a similar way, one obtains:

∗



∂U

∗

∂t

∗

∂U

∗

∂x

∗



= −

∆P

∂P

∗

∂x

∗

−

∂τ

∗

∂x

∗

+ ρ

∗

(7.12)

or once again rewritten in dimensionless form:

∗

⎛

⎜

⎝



∂U

∗

∂t

∗

+ U

∗

∂U

∗

∂x

∗

⎞

⎟

⎠

= −

∆P



∂P

∗

∂x

∗

−



1/Re

∂τ

∗

∂x

∗



1/Fr

∗

(7.13)

200 7 Similarity Theory

From (7.13), one can see that three new dimensionless characteristic numbers

were created by normalization of the momentum equation: from the continu-

ity equation and the momentum equation, four dimensionless characteristic

numbers can thus be derived for ﬂow problems:

St = L

= Strouhal number =

local acceleration forces

spatial acceleration forces

Eu = ∆P

/ρ

= Euler number =

pressure forces

acceleration forces

Re = ρ

/τ

= Reynolds number =

acceleration forces

molecular momentum transport

Fr = U

/(g

) = Froude number =

acceleration forces

mass forces

(7.14)

When one wants to obtain a general solution of (7.13), it is necessary

that the above-stated dimensionless characteristic numbers of the considered

ﬂow problems are equal. Naturally, this is only a necessary, but not suﬃ-

cient, requirement for the existence of a uniform solution for the considered

ﬂow problems. Similarity of the boundary conditions has to exist also and

this presupposes, in general, geometric similarity for the introduction of the

boundary conditions.

When one includes also into the consideration the momentum transport

relationship valid for a Newtonian medium:

= −µ



∂U

∂x

∂U

∂x



µδ

∂U

∂x

(7.15)

one obtains, by introducing dimensionless quantities,

∗

= −µ

∗

∂U

∗

∂x

∗

∂U

∗

∂x

∗

∂U

∗

∂x

∗

. (7.16)

Setting now τ

,oneobtainsRe =

with ν

, i.e. for

Newtonian media the following holds:

Re =

= Reynolds number, or L

. (7.17)

The dimensionless characteristic numbers stated above in (7.14) indicate

the conditions under which the dynamic similarity between ﬂows is given.

It means that the dimensionless characteristic numbers, introduced as force

relationships, adopt the same values. In the case of geometric similarity and

similar boundary conditions, i.e. for similar ﬂow problems, Re

= Re

= St

, Eu

= Eu

and Fr

= Fr

must hold. In this way, for exam-

ple, horizontal, stationary pipe ﬂows of gases and ﬂuids can be compared in

all their ﬂow properties when the same Reynolds numbers exist. The pressure

losses occurring in the pipe ﬂows can generally be plotted as

7.2 Dimensionless Form of the Diﬀerential Equations 201

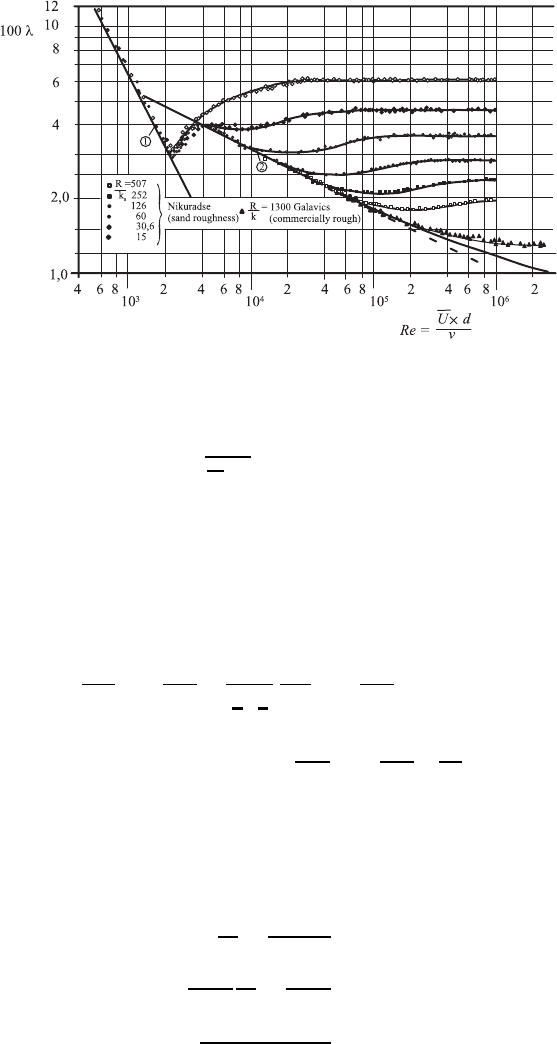
Fig. 7.2 Pressure loss factors for smooth and rough pipes for Newtonian ﬂuids. The

dimensionless presentation makes the generalization of measured values possible

∆P

=2Eu = f(Re). (7.18)

Thus c

values that were measured for an airstream can be employed for

the computation of pressure losses of ﬂows of diﬀerent Newtonian media, e.g.

water, oils, etc. When one considers also the inﬂuence of the “sand roughness”

on the pressure losses, see Fig. 7.2, pressure losses in smooth and rough

pipes results, with λ being equal to 4c

Extending the above similarity considerations also to the energy equation,

one obtains

∂T

∗

∂t

∗

+ U

∗

∂T

∗

∂x

∗

ReP r



 

∂

∂x

∗



∗



∂T

∗

∂x

∗



+ Ec



∂P

∗

∂t

∗

+ U

∗

∂P

∗

∂x

∗



. (7.19)

The normalization of the energy equation adds the following new di-

mensionless characteristic numbers to the similarity considerations valid

for momentum and heat transfers; ∆T

= T

− T

∞

is introduced for the

normalization of the temperatures:

Pr =

)

= Prandtl number

Pe = ReP r =

= Peclet number (7.20)

Ec =

)

− T

∞

)

=Eckertnumber.

202 7 Similarity Theory

The above dimensionless characteristic numbers can be grouped, as indicated

in Sect. 7.1:

1. Similarity of molecular transport processes: Pr,(Sc),...

2. Similarity of ﬂow processes: St,Re,Eu,Fr,(Gr)

3. Similarity of energy-transport processes: Pe,Ec,...

Finally, in the framework of the similarity of momentum and heat trans-

port processes, one should consider the dimensionless characteristic numbers

that result from experimental and theoretical investigations of heat transfer

processes. Extensions can easily be made to mass transfer processes. These

considerations result in the introduction of the Nusselt number (Nu)forthe

heat transfer and in the introduction of the Sherwood number (Sh)forthe

mass transfer. The considerations are limited at this point to the Nusselt

number. The heat transfer depends on the following parameters:

∞

|; |ρ|; |µ|; |L|; |D| with

Q(U

∞

,L,D, Fluid) results from measurements

of the heat transfer:

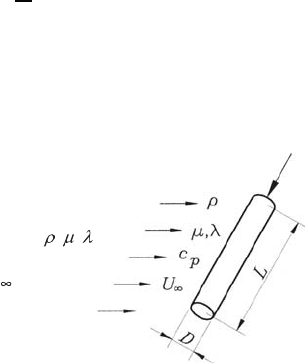
Q = heat supply to the cylinder shown in Fig. 7.3.

Sought is a method for the reduction of the number of measurements,

given by the set of parameters. Without similarity considerations, one has to

carry out many measurements

Q(U

∞

,L,D,Fluid).

The introduction of the Nusselt number is possible in many diﬀerent ways,

e.g. through similarity considerations in ﬂuid mechanics with heat transfer.

The introduction favored here starts from the following considerations of the

heat transfer from a cylinder (see Fig. 7.3).

In experimental investigations, the transfer of heat is measured per unit

area that can be expressed by a heat transfer coeﬃcient α and a temperature

diﬀerence between the surface and surrounding ﬂuid:

= α(πD)(T

− T

∞

), (7.21)

where

Q represents the transferred heat per unit time, L the length of the

cylinder, T

the temperature of the cylinder and T

∞

the temperature of the

oncoming ﬂuid far away from the cylinder.

The parameters

, , ,

c ,

describe the fluid and its

velocity

Fig. 7.3 Heat transfer considerations for a two-dimensional cylinder in a cross ﬂow

7.2 Dimensionless Form of the Diﬀerential Equations 203

α is deﬁned from experiments and without using similarity insights it

would have to be determined for all diameters D, for all ﬂuids of interest

and as a function of the incoming ﬂow velocity U

∞

. A generalization of the

information obtained through one series of measurements, i.e. for a single

ﬂuid, can be achieved by recognizing that the heat transfer rate per unit

length

Q/L supplied to the cylinder in Fig. 7.3 can be set equal to the removal

of heat conduction at the cylinder surface:

= −



∂T

∂r



r=R

. (7.22)

Thus the following relationship holds:

α(πD)(T

− T

∞

)=−



∂T

∂r



r=R

. (7.23)

When one introduces for the derivation of the dimensionless form of this

relationship the following quantities:

T =(T

− T

∞

∗

; r = Rr

∗

;

=(πR)dϕ

∗

; ϕ =2πϕ

∗

one obtains

α(πD)(T

−T

∞

−T

∞

)(πR)

⎡

⎣

−

∗



∂T

∗

∂r

∗



∗

dϕ

∗

⎤

⎦

(7.24)

or, rewritten:

Nu =

αD

= −

∗



∂T

∗

∂r

∗



∗

dϕ

∗

. (7.25)

The heat transfer obtained from a single series of measurements and for

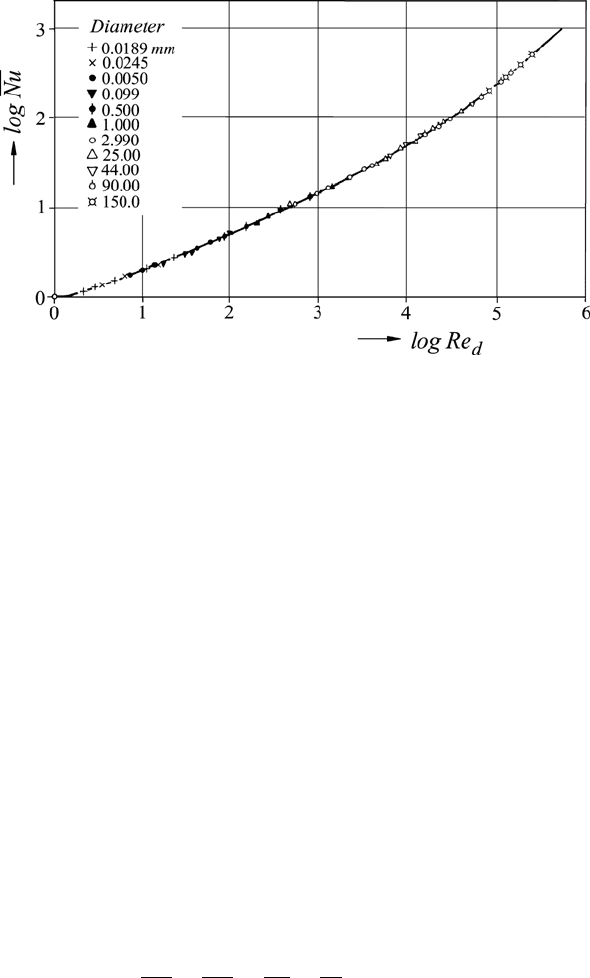
a single ﬂuid can be generalized by an Nu(Re) representation of the data.

Hilpert carried out experiments in an airstream and could thus cover an Re

domain of almost 10

, see ref. [7.5].

Equation (7.25) shows that heat transfer measurements can be generalized

when the results are given in terms of the Nusselt number and not by the

measured heat transfer coeﬃcient α. For the heat transfer problem considered

in Fig. 7.3, a correlation of the measuring results in the form Nu = f (Re)

is shown in Fig. 7.4. From a single series of measurements for an airstream,

a relationship can be derived that is valid for heat transfers from cylinders,

independent of the ﬂuid and the cylinder diameter.

Analogous to the introduction of the Nusselt number, considerations on

mass transfer can be carried out that lead to the introduction of the Sherwood

number as a fourth group of dimensionless characteristic numbers:

4. Similarity of integral heat and mass transfer: Nu,Sh

204 7 Similarity Theory

Fig. 7.4 Measured Nusselt numbers for the heat transfer into ﬂows around a cylinder

as a function of the Reynolds number

This classiﬁcation of dimensionless characteristic numbers represents the ba-

sis for deriving generally valid laws in ﬂuid mechanics from experiments,

analytical and numerical computations, carried out for special ﬂuids, in-

dividual ﬂow velocities and a limited set of geometric parameters. The

dimensionless presentation of results obtained, e.g. for one ﬂuid and one ﬂow

geometry by variation of the ﬂow velocity, can thus be transferred to other

ﬂuids and other similar ﬂow geometries of diﬀerent dimensions.

7.2.3 Considerations in the Presence of Geometric

and Kinematic Similarities

When solving ﬂuid mechanical problems, the question often arises of the

conditions under which the results of ﬂow investigations, obtained in a test

section, can be transferred to a second ﬂow with another ﬂuid and for the

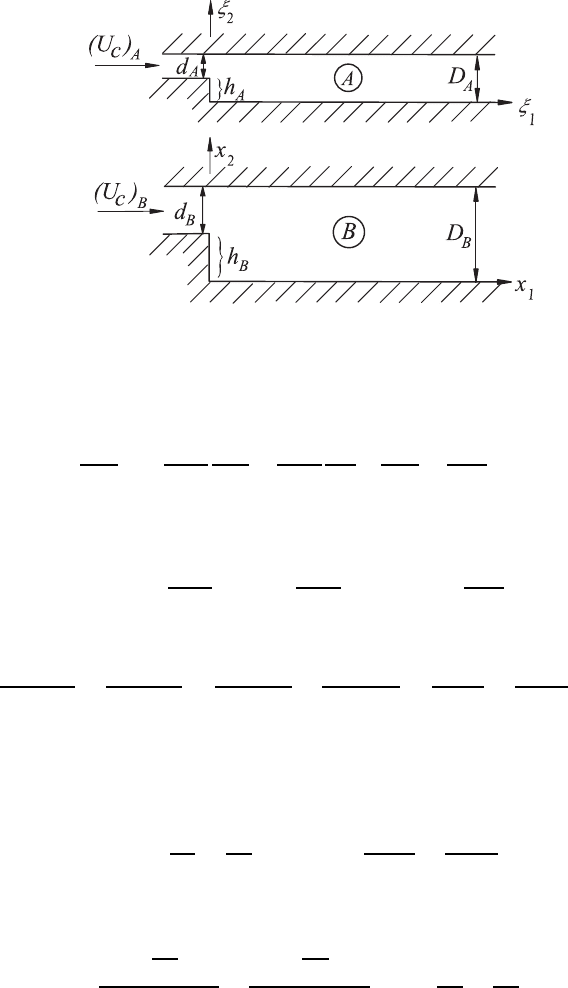
ﬂow in a geometrically similar test section. When considering in this context

the geometrically similar test section for step ﬂows sketched in Fig. 7.5 and

postulating stationary ﬂow conditions, geometric similarity demands that

the ratio of corresponding geometric dimensions of the test sections yields a

constant value

= constant. (7.26)

When one considers as characteristic linear measures of the ﬂow, the step

heights l

= h

and l

= h

and the corresponding characteristic ﬂow ve-

locities (U

)

=(U

)

and (U

)

=(U

)

, one obtains for the dimensionless

7.2 Dimensionless Form of the Diﬀerential Equations 205

Fig. 7.5 Diagram for similarity considerations at a step ﬂow

momentum equation, when assuming stationary ﬂow conditions, the following

form:

∗

∂U

∗

∂x

∗

= −

∆P

∂P

∗

∂x

∗

∂

∂x

∗

∂U

∗

∂x

∗

, (7.27)

i.e. for the dynamic similarity it is necessary that the following dimensionless

characteristic numbers are the same for both ﬂows:

Eu =

∆P

; Re =

;andFr =

. (7.28)

Thus for similar ﬂows one has to expect

∆P

)

∆P

)

;

)

;

)

. (7.29)

Large Froude numbers, i.e. high (U

)

or (U

)

values and small values of

or h

, result in a single dependency of all ﬂow quantities on the Reynolds

number. For (Re)

=(Re)

, the diﬀerential pressures obtained in a test

section can be transferred from one test section to the other:

for:

we have

∆P

. (7.30)

For the velocity proﬁle measured in the two test sections, the following

holds:







)







)

for

. (7.31)

The velocity proﬁles obtained in the two test sections are therefore similar

when they are measured in positions corresponding to similarity considera-

tions and when the measurements are taken with equal Reynolds numbers