Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows
Подождите немного. Документ загружается.


216 7 Similarity Theory
When one chooses as a third determinant variable g, it can be stated that
[g][h]
α
[µ]
β
[ρ]
γ
=1, (7.58)
i.e. (β + γ)=0;1+α − β − 3γ =0;−2 − γ =0.
Thus one obtains α =3; β = −2; γ =2, and therefore π
3
=
gh
3
ν
2
(7.59)
π
1
=
˙m
hµ
=[
kg
s
]
m · s
kg
1
m
= Re
(π
1
is the Reynolds number of the problem) (7.60)
π
2
=
A
h
2
=
7
m
2
8
1
m
2
(7.61)
π
3
=
gh
3
ν
2
π
1
= f(π
2
,π
3
). (7.62)
Hence a general representation of measured results can be achieved for
˙m = f(ρ, g, h, A, µ), such that one applies π
1
and chooses π
2
,π
3
as
parameters.
Example 2: Flow Through Rough Pipes
This is an example of high relevance to engineering:
number of the variables
Q
1
Q
2
Q
3
Q
4
Q
5
Q
6
˜
U
D ρ µ dP/dx
= roughness of the pipe
The parameters relevant for the representation of the problem of flow through
rough pipes were determined above. Thus the dimensional matrix can be
determined as follows:
˜
UdP/dxDρ µ
M 00 1 0 1 1
L
11 −21−3 −1 r =3 and n =6
T
−10 −200−1
When choosing
˜
U as a first determinant variable, one obtains
[
˜
U][D]
α
[ρ]
β
[µ]
γ
=(LT
−1
)(L
α
)(M
β
L
−3β
)(M
γ
L
−γ
T
−γ
)=M
0
L
0
T
0
(7.63)
i.e. (β + γ)=0;(1+α − 3β − γ)=0;(−1 − γ)=0.
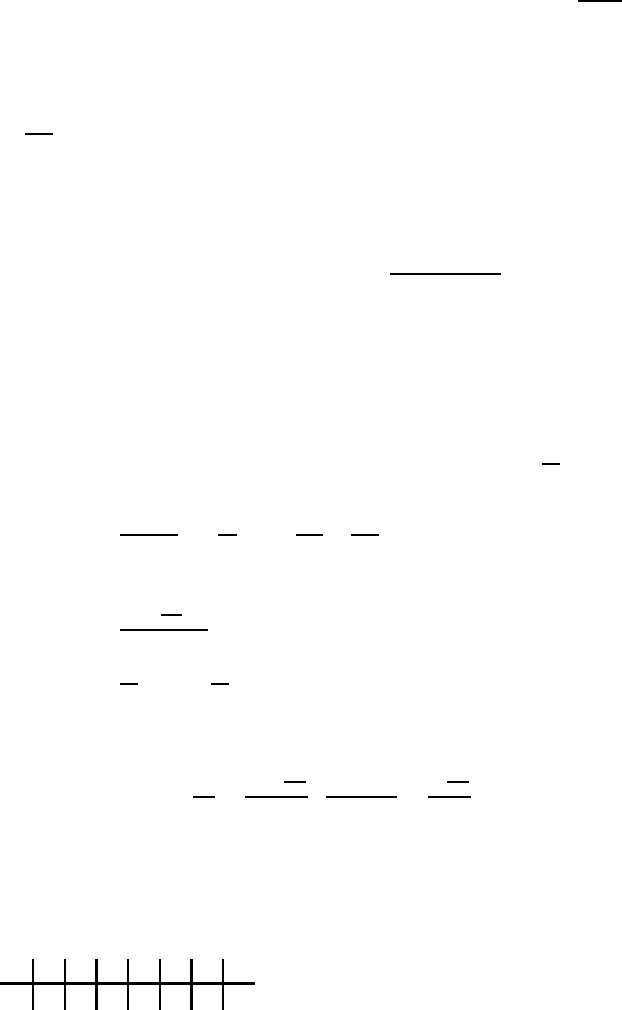
7.3 Dimensional Analysis and π-Theorem 217
Thus one obtains: γ = −1; β =1; α = 1 and therefore π
1
=
UDρ
µ
.
(7.64)
When choosing dP/dx as a second determinant constant, it can be stated
that
dP
dx
[D]
α
[ρ]
β
[µ]
γ
=
!
MT
−2
L
−1
"
(L
∞
)
!
M
β
L
−3β
"!
M
γ
L
−γ
T
−γ
"
, (7.65)
i.e. 1 + β + γ =0;−2+α − 3β − γ =0;−2 − γ =0.
Thus it can be computed that α =3; β =1; γ = −2; ;
π
2
=
(dP/dx)D
3
ρ
µ
2
. (7.66)
When one chooses as a third determinant variable, it yields
[D]
α
[ρ]
β
[µ]
γ
[]=(L
α
)(M
β
L
−3β
)(M
γ
L
−γ
T
−γ
)(L)=0, (7.67)
i.e. it holds that (α − 3β − γ +1)=0;β + γ =0;(−γ)=0.
Thus it results that γ =0; β =0; α = −1; ; π
3
=
D
(7.68)
π
1
=
U · Dρ
µ
=
m
s
[m]
kg
m
3
ms
kg
= Re
(π
1
is the Reynolds number of the problem) (7.69)
π
2
=
D
3
!
dP
dx
"
ρ
µ
2
= pressure-drop number (7.70)
π
3
=
D
=[m]
1
m
= “relative roughness” π
2
= f(π
1
; π
3
). (7.71)
However, instead of the characteristic number π
2
, the product
π
2
π
2
3
=
D
3
ρ
dP
dx
µ
2
·
µ
2
D
2
˜
U
2
ρ
2
=
D
dP
dx
ρU
2
can be used, as it was presented in Fig. 7.2.
Example 3: Pumping Capacity for an Incompressible Fluid
Q
1
Q
2
Q
3
Q
4
Q
5
Q
6
Q
7
Q
8
P
E
η g
H
ρ ω D
˙
V
µ

218 7 Similarity Theory
As the electrical pumping capacity is of special interest, it was also included
in the list of the relevant parameters. Thus the dimensional matrix can be
set up as follows:
P
E
ηg
H
ρωD
˙
Vµ
M 100100 01
L
20 2−301 3−1 r =3 and n =8
T
−30−20−10−1 −1
Consequent use of the methods indicated in Examples 1 and 2 leads to the
following characteristic numbers:
π
1
=
P
E
ρω
3
D
5
; π
2
= η; π
3
=
g
H
ω
2
D
2
; π
4
=
˙
V
ωD
3
; π
5
=
ρωD
2
µ
. (7.72)
The quantities to be ascertained as important for a pump, such as the
electrical power capacity P
E
, the efficiency factor η and the pump head g
H
,
can be represented via the following characteristic numbers:
P
E
ρω
3
D
5
= f
1
*
˙
V
ωD
3
;
ρωD
2
µ
+
= π
1
(7.73)
η = f
2
*
˙
V
ωD
3
;
ρωD
2
µ
+
= π
2
(7.74)
g
H
ω
2
D
2
=
*
˙
V
ωD
3
;
ρωD
2
µ
+
= π
3
. (7.75)
These characteristic numbers are dependent on the remaining character-
istic numbers π
4
and π
5
. From experiments, it is known, however, that
the dependence of the standardized pump properties does not depend on
π
5
=(ρωD
2
)/µ, or that the dependence is very small. Hence it can definitively
be stated that
P
E
ρω
3
D
5
= f
1
*
˙
V
ωD
3
+
; η = f
2
*
˙
V
ωD
3
+
;
g
H
ω
2
D
2
= f
3
*
˙
V
ωD
3
+
. (7.76)
The experimental results of pump investigations are generally also plotted as
indicated above, in diagrams with
˙
V/(ωD
3
) as abscissa.
References 219
References
7.1. Hutter, K., Fluid- und Thermodynamik: Eine Einf¨uhrung, Springer, Berlin
Heidelberg, 1995
7.2. Spurk, J.H., Dimensions analyse in der Str¨omungslehre, Springer, Berlin
Heidelberg, 1992
7.3. Zierep, J.,
¨
Ahnlichkeitsgesetze und Modellregeln der Str¨omungslehre, Braun,
Karlsruhe, 3. ¨uberarb. Auflage, 1991
7.4. Zlokarnik, M., Dimensional Analysis and Scale-Up in Chemical Engineering,
Springer, Berlin Heidelberg, 1991
7.5. Hilpert, R., W¨arme¨ubergang von geheizten Dr¨ahten and Rohren in Luftstorm.
Forsch. G. Ing, 4(5), pp 215–224, 1933
Chapter 8
Integral Forms of the Basic Equations
In Chap. 5, the basic equations of fluid mechanics were derived in a form valid
for all flow problems of Newtonian fluids. In order to obtain this generally
valid form of the equations, they were formulated as differential equations for
field quantities. They represent local formulations of mass, momentum and
energy conservations. Applying these equations to special flow problems, it is
advantageous and often essential to derive and employ the integral forms of
these equations. These are derived in this chapter from the basic differential
equations stated in Chap. 5 for a point in space, i.e. they are locally formu-
lated and are valid per unit volume. The integral form of these equations is
derived by integration over a pre-defined control volume. In the preceding
chapters these derivations take place separately for the continuity equation,
the momentum equation in direction j and the mechanical and caloric forms
of the energy equation. In the following sections exemplary applications are
described to make it clear how the applications of the derived integral forms of
the fluid-mechanical basic equations take place. It will thus be shown how it is
possible to solve fluid-mechanical problems in a somewhat engineering man-
ner. As in this book only an introduction to the solution of problems is given,
simplified assumptions are made in the course of the solutions. Attention is
drawn to these simplifications in order to ensure that the reader is aware of the
limits of the validity of the derived results. On the basis of the exemplary ap-
plications, independent solutions of more extensive and complicated problems
should be possible by readers of this book. Depending on the problem, the
integral form of the momentum equation or the mechanical energy equation
can be employed, since the latter results from the former, as shown in Chap. 5.
8.1 Integral Form of the Continuity Equation
In Sect. 5.2, the continuity equation, i.e. the mass-conservation equation in
the local formulation expressed in field variables, see equation (5.17), was
stated as follows:
221

222 8 Integral Forms of the Basic Equations
∂ρ
∂t
+
∂(ρU
i
)
∂x
i
=0. (8.1)
Applying to (8.1) the integral operator
'
V
K
()dV, i.e. integrating this equation
over a given control volume V = V
K
,oneobtains
#
V
K
∂ρ
∂t
dV +
#
V
K
∂(ρU
i
)
∂x
i
dV =0, (8.2)
where V
K
is an arbitrary control volume which is to be selected for the
solution of flow problems in such a way that a simple solution path for each
solved problem can be found.
Considering that the integration applied to (∂ρ/∂t) and the partial differ-
entiation carried out for ρ can be done in any sequence, one obtains
∂
∂t
(
#
V
K
ρ dV )+
#
V
K
∂(ρU
i
)
∂x
i
dV =0. (8.3)
Applying now, to the second term of the above equation, Gauss’s integral
theorem (see Sect. 2.9), the following equation results:
∂
∂t
(
#
V
K
ρ dV )+
#
O
K
ρU
i
dA
i
=0. (8.4)
Here the second integral is to be carried out over the entire outer surface of
the control volume, where the direction of dF
i
is considered positive from
the inside of the volume to its outside.
In (8.2), the following consideration was applied:
#
V
K
∂ (ρU
i
)
∂x
i
dV ⇐⇒
#
O
K
(ρU
i
)dA
i
• In this relationship the surface vector dF
i
represents a directed quantity,
i.e. it contains the normal vector n of the surface element with its absolute
value |dA
i
|.
• Because of the double index we have a scalar product of the velocity vector
U
i
with the surface vector dA
i
.
In (8.4), the resulting integrals have the following meaning:
M =
#
V
K
ρ dV = total mass in the control volume,
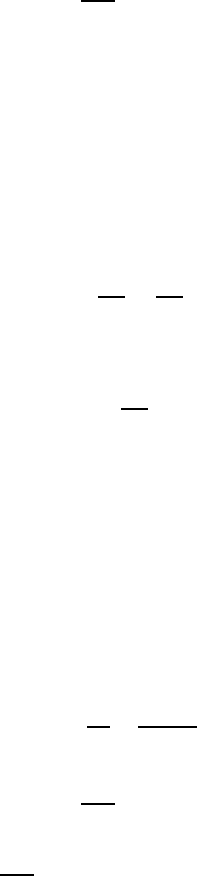
8.1 Integral Form of the Continuity Equation 223
˙m
out
− ˙m
in
=
#
O
K
ρU
i
dA
i
=
difference of the mass outflows and inflows
over the surface of the control volume
.
(8.5)
Thus the integral form of the continuity equation yields:
∂M
∂t
=˙m
in
− ˙m
out
. (8.6)
For the volume flow through a surface with the velocity component U
i
normal
to this surface, one obtains, because of the above sign convention for the
surface vector dA
i
(outer normal to the surface), for the inflow in the control
volume or the outflow from it:
˙
V
in
= −
#
F
|U
i
||dA
i
|
˙
V
out
=+
#
F
|U
i
||dA
i
|. (8.7)
The surface-averaged flow velocity can therefore be computed for any point
in time at
˜
U =
˙
V
in
|A|
=
1
|A|
#
F
U
i
dF
i
. (8.8)
When one considers, however, that for the area-averaged density ˜ρ
˜ρ =
1
|A|
#
F
ρ |dA
i
|, (8.9)
the mass flow through a surface can also be written:
| ˙m| =˜ρ
˜
UF mit F = |F |. (8.10)
For moderate velocities, where ρ is hardly changing, for internal flows, a
surface decrease is connected with an increase in velocity.
When carrying out considerations in fluid mechanics, the above deriva-
tions, taking into account the physical conditions of mass conservation, lead
to the following mathematical representations of mass conservation:
Differential form:
∂ρ
∂t
+
∂(ρU
i
)
∂x
i
=0. (8.11)
Integral form:
∂M
∂t
=˙m
in
− ˙m
out
. (8.12)
Internal flows:
∂M
∂t
=0 ; ˙m =˜ρ
˜
UA = constant (8.13)

224 8 Integral Forms of the Basic Equations
From (8.13) one can derive by differentiating
d
dx
(˙m)=
d
dx
(˜ρ
˜
UF)=0 ;
d˜ρ
˜ρ
+
d
˜
U
˜
U
+
dF
F
= 0 (8.14)
All of the above equations represent different forms of mass conservation
that can be employed for the solution of flow problems; which form should
be chosen depends on the method that is applied to solve a particular flow
problem.
8.2 Integral Form of the Momentum Equation
In Sect. 5.3, the momentum equation for local considerations of flow prob-
lems was formulated and derived for each component j of the momentum as
follows, i.e. for j =1, 2, 3:
ρ
∂U
j
∂t
+ U
i
∂U
j
∂x
i
= −
∂P
∂x
j
−
∂τ
ij
∂x
i
+ ρg
j
. (8.15)
When one adds to this equation the continuity equation in the form (8.1),
multiplied by U
j
, i.e. adding the following terms:
U
j
∂ρ
∂t
+ U
j
∂(ρU
i
)
∂x
i
=0, (8.16)
one obtains
∂(ρU
j
)
∂t
+
∂(ρU
i
U
j
)
∂x
i
= −
∂P
∂x
j
−
∂τ
ij
∂x
i
+ ρg
j
. (8.17)
When integrating (8.17) over a given control volume, i.e. when applying the
operator
'
V
K
() dV to all terms of the equation, one obtains the integral form
of the component j of the momentum equation of fluid mechanics:
#
V
K
∂(ρU
j
)
∂t
dV +
#
V
K
∂(ρU
i
U
j
)
∂x
i
dV = −
#
V
K
∂P
∂x
j
dV −
#
V
K
∂τ
ij
∂x
i
dV +
#
V
K
ρg
j
dV +
F
j
.
(8.18)
The term
K
j
is added as “integration constant”, i.e. all those forces in the
direction j have to be included in the equation that act as external forces on
the boundaries of the chosen control volume. Considering that the integration
and differentiation represent in their sequence exchangeable mathematical op-
erators, and also employing Gauss’s integration theorem, the following form
of the integral momentum equation can be derived:
∂
∂t
#
V
K
ρU
j
dV
I
+
#
O
K
ρU
i
U
j
dF
i
II
= −
#
O
K
P dF
j
III
−
#
O
K
τ
ij
dF
i
IV
+
#
V
K
ρg
j
dV
V
+
F
j
VI
.
(8.19)
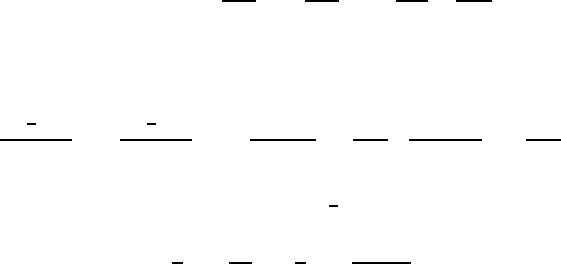
8.3 Integral Form of the Mechanical Energy Equation 225
This equation comprises six terms whose physical meanings are stated below:
I: Temporal change of the j momentum in the interior of a control volume.
II: Sum of inflows and outflows of flow momentum per unit time in the
direction j summed up over the entire surface surrounding the considered
control volume. The momentum over i =1, 2, 3 represents this.
III: Resulting pressure force in the direction j, obtained by integration
over the entire j components of the surface elements surrounding the
considered control volume.
IV: Sum of the j momentum inflows and outflows occurring per unit time
by molecular momentum transport over the entire surface of the control
volume. The double index i expresses the summation over 1, 2, 3.
V: The j component of the mass force acting on the control volume.
VI: Sum of all external (not fluid mechanically induced) forces acting in the
j direction on the boundaries of the control volume.
This integral form of the momentum equation can be employed for a large
number of flow problems in fluid mechanics, in order to determine the cause
of forces on fluid motions on walls, flow aggregates, etc. Their applica-
tion is explained in the examples that are dealt with in Sects. 8.5.1–8.5.9.
On the basis of selected representative samples, it will be made clear how
the above-derived integral form of the momentum equation can be used to
solve flow problems. Here it is important to recognize the universal valid-
ity of the integral form of the momentum equation to ensure its general use
in solving flow problems, beyond the examples considered in the following
sections.
8.3 Integral Form of the Mechanical Energy Equation
In Sect. 5.5, it was shown that the momentum equation j:
in differential form : ρ
∂U
j
∂t
+ U
i
∂U
j
∂x
i
= −
∂P
∂x
j
−
∂τ
ij
∂x
i
+ ρg
j
(8.20)
can be transferred to the mechanical energy equation by multiplication by
U
j
, [see (5.56)], to yield the following relationship:
ρ
3
∂
!
1
2
U
2
j
"
∂t
+ U
i
∂
!
1
2
U
2
j
"
∂x
i
4
= −
∂(PU
j
)
∂x
j
+P
∂U
j
∂x
j
−
∂(τ
ij
U
j
)
∂x
i
+τ
ij
∂U
j
∂x
i
+ρg
j
U
j
.
(8.21)
Multiplying the continuity equation by (
1
2
U
2
j
), the following results:
1
2
U
2
j
∂ρ
∂t
+
1
2
U
2
j
∂(ρU
i
)
∂x
i
=0, (8.22)

226 8 Integral Forms of the Basic Equations
which can be added to (8.21) so that one obtains
∂
∂t
1
2
ρU
2
j
+
∂
∂x
i
ρU
i
1
2
U
2
j
= −
∂(PU
j
)
∂x
j
+P
∂U
j
∂x
j
−
∂(τ
ij
U
j
)
∂x
i
+τ
ij
∂U
j
∂x
i
+ρg
j
U
j
.
(8.23)
When one integrates this equation over a given control volume, one obtains,
by employing Gauss’s integral theorem and taking into account the mathe-
matically possible inversion of the integration and differentiation sequence:
∂
∂t
#
V
K
1
2
ρU
2
j
dV
I
+
#
O
K
ρU
i
1
2
U
2
j
dA
i
II
= −
#
O
K
PU
j
dA
j
III
+
#
V
K
P
∂U
j
∂x
j
dV
IV
−
#
O
K
τ
ij
U
j
dA
i
V
+
#
V
K
τ
ij
∂U
j
∂x
i
dV
VI
+
#
V
K
ρg
j
U
j
dV
VII
+
˙
E
VIII
. (8.24)
This equation comprises eight terms having the following physical meanings:
I: Temporal change of the entire kinetic energy of the flowing fluid within
the limits determining the control volume.
II: Outflow minus inflow of the kinetic energy of the flowing fluid per unit
time over the entire surface of the considered control volume.
III: Inflow minus outflow of “pressure energy” per unit time over the entire
surface of the considered control volume.
IV: Work done by expansion of the flowing fluid per unit time integrated
overtheentirecontrolvolume.
V: Molecule-dependent input minus output of kinetic energy of the con-
sidered flowing fluid per unit time integrated over the entire surface of
the control volume.
VI: The kinetic energy per unit time dissipated within the entire control
volume. This energy is transferred into heat.
VII: Potential energy per unit time of the total mass then integrated over
the entire control volume.
VIII: Energy input per unit time over the surface of the control volume or
the power supplied to the fluid by flow machines.
In Sect. 5.5, attention was drawn to the fact that the differential form of the
j momentum equation and the differential form of the mechanical energy
equation do not represent independent equations. The latter emanated from
the first by multiplication by U
j
, followed by various mathematical deriva-
tions and rearrangements of the different terms. This statement holds only
in a restricted way for the integral form of the basic equations. By addi-
tion of the term
F
j
in (8.19) and the term
˙
E in (8.24), it is possible
that independent forms of the momentum equation and the mechanical en-
ergy equation come about. This is known from the treatment of impacts
