Durst F. Fluid Mechanics: An Introduction to the Theory of Fluid Flows

Подождите немного. Документ загружается.

References 461

U d

of order 1

Undisturbed

oncoming flow

Boundary of region with

velocity and temperature

influence

Cylinder

(

)

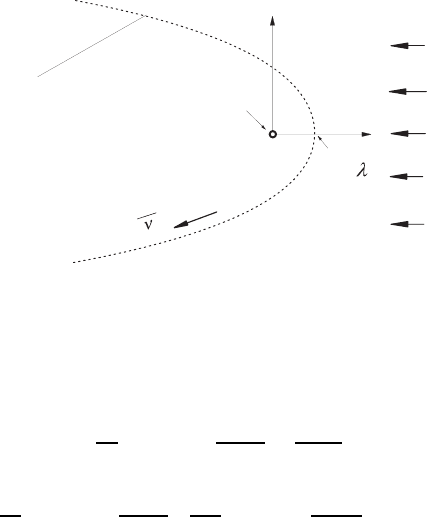
Fig. 15.14 Finite area for the dissipation of heat or rotational momentum for small

Reynolds numbers

cylinder the area in which inﬂow conditions have to be imposed that are not

disturbed by the cylinder. According to (15.193), one obtains





> const

∞

const

(15.194)





> const

∞



µc



=const

RePr

. (15.195)

Equation (15.194) shows that with decreasing Reynolds number the inte-

gration area increases, which has to be covered with a numerical grid when

numerical integration procedures are employed, in order to install the bound-

ary conditions holding at inﬁnity. An additional extension of the computation

area results for Peclet numbers, Pe=(ReP r) < 1, i.e. for Pr < 1, when the

temperature ﬁeld of a ﬂow around a cylinder also has to be computed.

References

15.1. F.S. Sherman: “Viscous Flow” McGraw Hill, New York, 1990

15.2. S.W. Yuan: “Foundations of Fluid Mechanics”, Civil Engineering and

Mechanics Series, Mei Ya, Taipei, Taiwan (1971)

15.3. H. Lamb: “On the Uniform Motion of a Sphere Through a Viscous Fluid”, Phil.

Mag. 21, p. 120 (1911)

15.4. H. Lamb: “Hydrodynamics”, Dover, New York, 1945

15.5. H. Schlichting: “Boundary Layer Theory”, 6th Edition, McGraw Hill, New York

(1968)

15.6. R.B. Bird, W.E. Stewart, E.N. Lightfoot: “Transport Phenomena”, Wiley, New

York (1960)

15.7. C.S. Yih: “Fluid Mechanics - A Concise Introduction to the Theory”, West

River, Ann Arbor, MI, 1979

15.8. M. van Dyke: “The Album of Fluid Motion”, The Parabolic Press, Stanford,

California, 1982

Chapter 16

Flows of Large Reynolds Numbers

Boundary-Layer Flows

16.1 General Considerations and Derivations

In Chap. 15, ﬂows that were characterized by small Reynolds numbers (Re)

were considered, i.e. ﬂuid ﬂows were treated that were diﬀusion-dominated

and where convection played a secondary role. This can be expressed by small

Re,e.g.whentakingRe as a ratio of forces:

Re =

acceleration forces

viscosity forces

, (16.1)

where ρ

and µ

represent the density and viscosity characterizing a ﬂuid,

respectively, U

represents a characteristic velocity and L

is a length

characterizing the ﬂow domain.

Equivalent considerations on the signiﬁcance of Re can, however, also be

expressed by the ratio of times typical for diﬀusion and convection processes

in the considered ﬂuid ﬂows:

Re =

/ν

diﬀusion times

convection times

(16.2)

or by the corresponding velocities that are typical for diﬀusion and convection

processes:

Re =

convection velocities

diﬀusion velocities

. (16.3)

Considering ﬂows of large Re, i.e. ﬂows in which the acceleration forces are

large in comparison with the viscous forces, or in which the diﬀusion times

are large in comparison with the convection times, or the convection velocities

are large in comparison with the diﬀusion velocities, it can be shown that,

e.g., the inﬂuences of wall boundaries on ﬂows are limited to small areas near

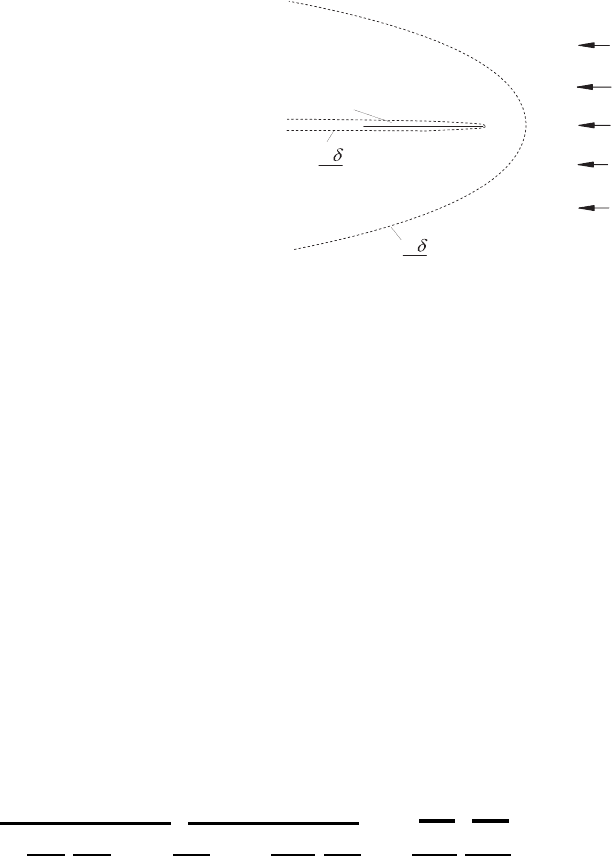
the walls. This is sketched in Fig. 16.1, which shows the ﬂow around a ﬂat

plate and indicates there the small region near the wall, where viscous inﬂu-

ences can be observed. The contents of this ﬁgure results from the extended

463

464 16 Flows of Large Reynolds Numbers

Fig. 16.1 Area limitations for diﬀu-

sion processes with Re ≈ 1andin

the case of a ﬂow around a plate for

Re  1

Undisturbed

flow

Wall near region for

high

-numbers

considerations which were carried out at the end of Chap. 15. Applying the

insights gained from Sect. 15.9 to the ﬂow around a ﬂat plate, a large region

results for Re ≈ 1, in which diﬀusion processes are present. In this region,

information about the presence of the plate (around which the ﬂow passes)

is available. When, on the other hand, conditions exist that are character-

ized by Re  1, the inﬂuence of the diﬀusion remains restricted to a small

region very close to the plate. There, a so-called wall boundary layer forms.

Boundary layers of this kind are thus the characteristic properties of ﬂows

of high Re. Such ﬂows can therefore be subdivided into body-near regions,

where viscous inﬂuences on ﬂows have to be considered, and regions that

are distant from the wall, which can be regarded as being free from viscous

inﬂuences.

The above considerations show clearly that special treatments are neces-

sary, in order to derive the equations that can be employed as approximations

of the Navier–Stokes equations for Re  1 to solve ﬂow problems. Looking

for derivations where the viscous terms, because Re  1, are completely ne-

glected in the diﬀerential equations describing the ﬂow results in the Euler

equations:

standardized Euler equation

  

∗



∂U

∗

∂t

∗

+ U

∗

∂U

∗

∂x

∗



= −

∆P

∂P

∗

∂x

∗

⇒0 because Re⇒∞

  

∂

∗

∂x

∗

. (16.4)

These equations are not applicable to solving wall boundary-layer ﬂow prob-

lems. For the derivation of the boundary-layer equations, one has rather to

apply considerations as proposed by Prandtl (1904, 1905). They are based on

order of magnitude considerations of the terms in the Navier–Stokes equa-

tions, taking into consideration the diﬀerences in the times and velocities

in diﬀusion and convection transport processes. If one neglects the viscous

terms entirely, this would be equivalent to a reduction of the order of the

16.1 General Considerations and Derivations 465

Point at edge

of boundary layer

Start of flat plate

= x where x = the boundary-layer coordinate in the ﬂow direction

= y where y = the boundary-layer coordinate vertical to the ﬂow direction

Fig. 16.2 Boundary-layer thickness along a plane ﬂat plate and its development

basic equations describing the ﬂuid ﬂow. Hence it would not be possible to

implement all the boundary conditions characterizing a ﬂow, and ﬂows that

result in this way from the diﬀerential equations as solutions would show

considerable deﬁcits.

The transition from the generally valid Navier–Strokes equations to the

boundary-layer equations, as indicated in Fig. 16.1, is an essential step which

has to be taken into consideration, in order to admit only such simpliﬁcations

of the Navier–Stokes equations which result in physically still reasonable

solutions. The resultant equations are called the boundary-layer equations.

When choosing L as a distance in the ﬂow direction along the ﬂat plate ﬂow

indicated in Fig. 16.2, δ is the resultant boundary-layer thickness, Fig. 16.1

showing that δ  L holds for large Re. Considering the times:

∆t

= L/U

∞

convection time,

∆t

= δ

/ν diﬀusion time

one obtains, as ∆t

= ∆t

for the boundary point δ(L):

∞

;

∞

. (16.5)

The boundary-layer thickness δ, normalized with the development length,

is proportional to the reciprocal of the Reynolds number, formed with the ex-

ternal ﬂow velocity and the boundary-layer thickness: (δ/L)=1/Re

.Paying

attention to the context in (16.3), it results for the diﬀusion velocity occur-

ring in the y-direction that U

= U

≈ ν/δ, so that for considerations of

the orders of magnitude of the terms in the Navier–Stokes equations, the

following normalization can be carried out:

∗

; y

∗

; U

∗

∞

; U

∗

ν/δ

; t

∗

L/U

∞

; P

∗

∞

(16.6)

466 16 Flows of Large Reynolds Numbers

Introducing these normalized quantities into the two-dimensional Navier–

Stokes equations with constant ﬂuid properties:

∂U

∂x

∂U

∂x

=0, (16.7)



∂U

∂t

+ U

∂U

∂x

+ U

∂U

∂x



= −

∂P

∂x

+ µ



∂

∂x

∂

∂x



, (16.8)



∂U

∂t

+ U

∂U

∂x

+ U

∂U

∂x



= −

∂P

∂x

+ µ



∂

∂x

∂

∂x



(16.9)

the below-stated derivations can be carried out and for the continuity

equation one obtains:

∞

∂U

∗

∂x

∗

∂U

∗

∂y

∗

=0 ;

∂U

∗

∂x

∗

νL

∞

 

≈1

∂U

∗

∂y

∗

=0, (16.10)

where the term νL/U

∞

=(L/U

∞

)/(δ

/ν) is the relationship for the ratio

of the convection and diﬀusion times. According to (16.5), both terms are

equal, so that both gradients in the continuity equation are of the same order

of magnitude and therefore have to be carried along in the boundary-layer

equations. Thus the continuity equation for boundary-layer ﬂows reads:

∂U

∂x

∂U

∂y

=0. (16.11)

For the momentum equation in the x-direction, the normalization yields:



∞

∂U

∗

∂t

∗

∞

∗

∂U

∗

∂x

∗

νU

∞

∗

∂U

∗

∂y

∗



= −

∞

∂P

∗

∂x

∗

+ µ



∞

∂

∗

∂x

∗

∞

∂

∗

∂y

∗



. (16.12)

On dividing the entire equation by ρU

∞

/L,oneobtains:

∂U

∗

∂t

∗

+ U

∗

∂U

∗

∂x

∗

νL

∞

 

≈1

∗

∂U

∗

∂y

∗

= −

∞

ρU

∞

∂P

∗

∂x

∗

∞





δ/(LRe

)

∂

∗

∂x

∗

νL

∞

 

≈1

∂

∗

∂y

∗

. (16.13)

With δ/L ≈ 1/Re

, the ﬁrst of the two viscous terms in (16.13), multiplied

by 1/Re

, can be regarded as negligible for Re

 1. Thus for the boundary

16.1 General Considerations and Derivations 467

layer form of the x-momentum equation the following equation holds:



∂U

∂t

+ U

∂U

∂x

+ U

∂U

∂y



= −

∂P

∂x

+ µ

∂

∂y

. (16.14)

Analogous derivations yield for the two-dimensional y-momentum equation:



νU

∞

δL

∂U

∗

∂t

∗

∞

δL

∗

∂U

∗

∂x

∗

∂U

∗

∂y

∗



= −

∞

∂P

∗

∂y

∗

+ µ

δL

∂

∗

∂x

∗

∂

∗

∂y

∗

. (16.15)

On dividing this equation also by ρU

∞

/L, the following equation results:

δU

∞

∂U

∗

∂t

∗

δU

∞

∗

∂U

∗

∂x

∗

∞

νL

∞

 

≈1

∗

∂U

∗

∂y

∗

= −

∞

ρU

∞

∂P

∗

∂y

∗

∞

∂

∗

∂x

∗



∞



∂

∗

∂y

∗

(16.16)

or rewritten:



∂U

∗

∂t

∗

+ U

∗

∂U

∗

∂x

∗

+ U

∗

∂U

∗

∂y

∗



= −

∞

ρU

∞

∂P

∗

∂y

∗

∂

∗

∂x

∗

∂

∗

∂y

∗

. (16.17)

From (16.17), it can be seen that all acceleration and viscous terms can be

neglected when compared with terms in (16.14). Because Re  1, they are

very small in comparison with the corresponding terms in the x-momentum

equation (16.14). Thus the y-momentum equation results in the following

equation:

∂P

∂y

=0. (16.18)

This equation expresses the fact that the pressure in a boundary layer, vertical

to the ﬂow direction, does not change. The boundary layer thus experiences,

up to the wall, the pressure change imposed in the x-direction on the outer

ﬂow. This means for many problem solutions that the pressure distribution

P (x, y)=P

∞

(x) is known, so that, through the boundary-layer equations for

the solution of ﬂow problems, only the velocity components U

and U

have

to be determined.

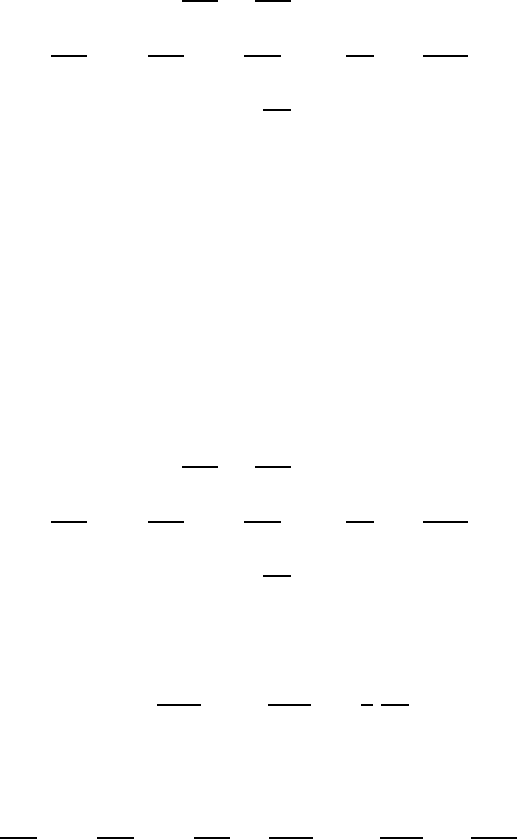
468 16 Flows of Large Reynolds Numbers

Looking at the above derivations, the two-dimensional boundary-

layer equations can be stated as follows, on the basis of the above

order-of-magnitude considerations:

∂U

∂x

∂U

∂y

=0, (16.19a)



∂U

∂t

+ U

∂U

∂x

+ U

∂U

∂y



= −

∂P

∂x

+ µ

∂

∂y

, (16.19b)

∂P

∂y

=0. (16.19c)

Equations (16.19) are, as can easily be shown, a set of parabolic diﬀerential

equations. They can be solved with the corresponding boundary conditions

for some ﬂow geometries and thus make it possible to compute the velocity

distributions in boundary-layer ﬂows with simpler equations than the Navier–

Stokes equations. There are numerous text books that describe the above

boundary-layer equations, e.g. see refs [16.4] to [16.9]

16.2 Solutions of the Boundary-Layer Equations

In the preceding section the boundary-layer equations were derived:

∂U

∂x

∂U

∂y

=0, (16.20a)



∂U

∂t

+ U

∂U

∂x

+ U

∂U

∂y



= −

∂P

∂x

+ µ

∂

∂y

, (16.20b)

∂P

∂y

=0. (16.20c)

For the outer ﬂow, where no viscous eﬀects occur, the pressure distribution

can be determined through the Euler form of the momentum equation:

∂U

∞

∂t

+ U

∞

∂U

∞

∂x

= −

∂P

∂x

. (16.21)

Because of (16.20c), the momentum equation (16.20b) can be written as

follows, taking (16.21) into account:

∂U

∂t

+ U

∂U

∂x

+ U

∂U

∂y

∂U

∞

∂t

+ U

∞

∂U

∞

∂x

+ ν

∂

∂y

. (16.22)

It is necessary to solve this equation together with (16.20a), in order to

compute boundary-layer ﬂows. However, the validity of this equation has

strictly been veriﬁed only for Cartesian coordinates. It should be pointed

out, however, that it holds also for curved coordinates, when the radius of

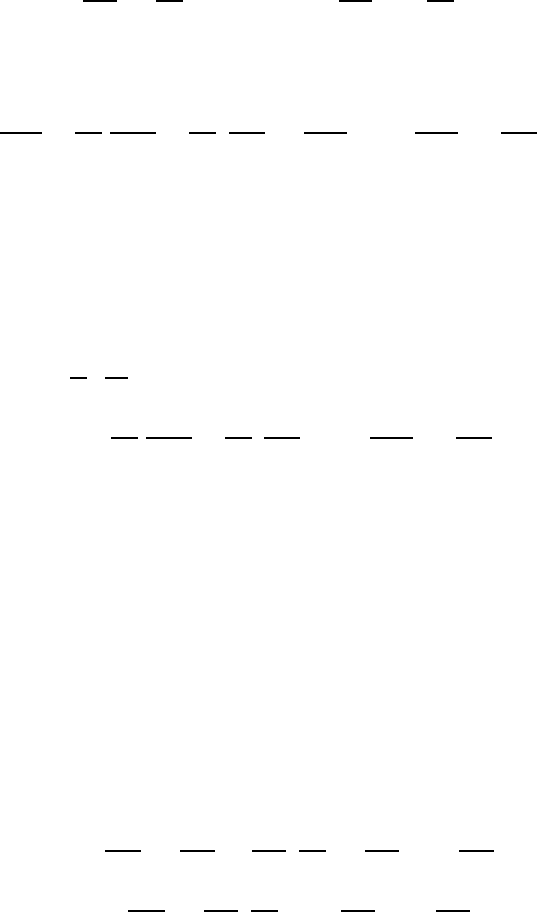
16.2 Solutions of the Boundary-Layer Equations 469

curvature of the ﬂow lines is large in comparison with the boundary layer

thickness δ.

In order to solve the boundary layer equation, it is recommended to

introduce the stream function Ψ , so that the continuity equation is eliminated:

∂Ψ

∂x

∂Ψ

∂y

= U

; U

= −

∂Ψ

∂x

= −

∂Ψ

∂x

= U

. (16.23)

Thus, according to (16.22), the following partial diﬀerential equation for the

stream function Ψ can be derived:

∂

∂t∂y

∂Ψ

∂y

∂

∂x∂y

−

∂Ψ

∂x

∂

∂y

∂U

∞

∂t

+ U

∞

∂U

∞

∂x

+ ν

∂

∂y

. (16.24)

We therefore have to deal with a partial diﬀerential equation of third order,

which has to be solved for the stream function Ψ (x, y, t). Hence the solution

of the equation requires one to state three boundary conditions and suitable

initial conditions. Attention has to be paid to the fact that the diﬀerent

boundary-layer ﬂows are given by the corresponding boundary and initial

conditions. The transport processes occurring in the boundary-layers are all

described, however, by the diﬀerential equation for Ψ.

When stationary ﬂow conditions exist, from (16.24) the following equation

results for

∂

∂t

∂Ψ

∂x

=0:

∂Ψ

∂y

∂

∂x∂y

−

∂Ψ

∂x

∂

∂y

= U

∞

+ ν

∂

∂y

. (16.25)

This equation was stated by Blasius (1908) for the case of a ﬂow over a plane

plate with U

∞

= constant and was also solved by him analytically.

For the case of stationary boundary layer ﬂows, von Mises (1927) at-

tributed the boundary-layer equations to a non-linear partial diﬀerential

equation of second order, which corresponded to the equation typical for heat

conduction. The essential points of the derivation of the von Mises diﬀerential

equation can be summarized as shown below.

The derivations proposed by von Mises start also from the stream func-

tion Ψ , which is, however, introduced into the derivation as an independent

variable, so that the following holds:

(x, y)=V

(x, Ψ)andU

(x, y)=V

(x, Ψ). (16.26)

With this, the relationships below can be stated:

∂U

∂x

∂V

∂x

∂V

∂Ψ

∂x

∂V

∂x

− U

∂V

∂Ψ

, (16.27)

∂U

∂y

∂V

∂Ψ

∂y

= U

∂V

∂Ψ

= V

∂V

∂Ψ

. (16.28)

470 16 Flows of Large Reynolds Numbers

For the second derivatives with respect to y, one obtains the following

intermediate result:

∂

∂y

∂

∂y



∂U

∂y



∂

∂y



∂V

∂Ψ



= U

∂V

∂Ψ

+ U



∂V

∂Ψ



= U

∂V

∂Ψ



∂V

∂Ψ



= U

∂

∂Ψ



∂V

∂Ψ



. (16.29)

Thus the following second derivative can be deduced:

∂

∂y

= U

∂

∂Ψ



∂

∂Ψ





= V

∂

∂Ψ





. (16.30)

On inserting (16.27)–(16.30) into the boundary layer form of the stationary

momentum equation, the following results:

∂V

∂x

= U

∞

+ νV

∂

∂Ψ





(16.31)

or rewritten:

∂V

∂x

∞

+ νV

∂

∂Ψ

. (16.32)

If one now introduces a new function:

V(x, Ψ)=U

∞

− V

(16.33)

so that V



∞

−V holds, the diﬀerential equation (16.32) adopts the

so-called von Mises form:

∂V

∂x

= ν



∞

−V

∂

∂Ψ

. (16.34)

The von Mises diﬀerential equation has to satisfy the boundary conditions:

Ψ =0: U

=0, i.e. V = U

∞

Ψ →∞: U

→ U

∞

, i.e. V =0.

(16.35)

The above general solution ansatz for the boundary layer equations are

applied to diﬀerent ﬂows in subsequent chapters.

16.3 Flat Plate Boundary Layer (Blasius Solution)

The ﬂow over a ﬂat plate, sketched in Fig. 16.3, represents the ﬂow of a ﬂuid

having constant ﬂuid properties and also a constant inﬂow velocity. This

inﬂow hits, at the origin of the x–y coordinate system, an inﬁnitely extended

16.3 Flat Plate Boundary Layer (Blasius Solution) 471

( y)

for

x = constant

{

Fig. 16.3 Formation of a plate boundary layer with

∂P

∂x

=0and

∞

ﬂat plate, positioned in the x–y coordinate system, so that along the ﬂat plate

a boundary layer ﬂow forms. For the latter the boundary layer equations

(16.20a)–(16.20c) hold, with the simpliﬁcations according to (16.21):

∂P

∂x

= 0 (16.36)

and

∂U

∞

∂x

∞

= 0 (16.37)

so that the boundary layer equations hold as follows:

∂U

∂x

+ U

∂U

∂y

= ν

∂

∂y

, (16.38)

∂U

∂x

∂U

∂y

= 0 (16.39)

with the boundary conditions:

y =0: U

= U

=0 and y →∞: U

→ U

∞

. (16.40)

On introducing the stream function Ψ for the elimination of the continuity

equation:

∂Ψ

∂y

and U

= −

∂Ψ

∂x

(16.41)

one obtains the following diﬀerential equation for the x-momentum transport:

∂Ψ

∂y

∂

∂x∂y

−

∂Ψ

∂x

∂

∂y

= ν

∂

∂y

. (16.42)

Blasius proposed a similarity solution for (16.42), such that the solution was

obtained with the ansatz

∞

= F (η) with η = y

∞

νx

. (16.43)