Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics
Подождите немного. Документ загружается.


28 Part A Mathematical Methods
Symmetry relation:
#
D
j
(Z)
$
T
= D
j
Z
T
.
Generation from highest weight:
D
j
mm
(Z) =
( j +m)!
(2 j)!( j −m)!
×
( j +m
)!
(2 j)!( j −m
)!
1
2
× M
j−m
−
K
j−m
−
D
j
jj
(Z).
Generating functions:
(x
T
Zy)
2 j
/(2 j)!=
mm
P
jm
(x)D
j
mm
(Z)P
jm
( y),
exp(tx
T
Zy) =
j
t
2 j
mm
P
jm
(x)D
j
mm
(Z)P
jm
( y),
x = col(x
1
x
2
), y = col(y
1
y
2
),
Z =
z
α
i
, i,α= 1, 2 ; all indeterminates .
2.5 Differential Operator Realizations of Angular Momentum
Differential operators realizing the standard commu-
tation relations (2.7)and(2.8) can be obtained from
the 2-spinorial realizations given in Sect. 2.4.4 by
specializing the matrix Z to the appropriate unitary uni-
modular matrix U ∈ SU(2) and using the chain rule
of elementary calculus. Similarly, one obtains the ex-
plicit functions D
j
mm
simply by substituting for Z the
parametrized U in (2.24). This procedure is used in this
section to obtain all the realizations listed. The notations
M = (M
1
, M
2
, M
3
) and K = (K
1
, K
2
, K
3
) and the as-
sociated M
±
and K
±
refer to the differential operators
given by the 2-spinorial realization now transformed to
the parameters in question.
Euler angles with Z =U(αβγ) (Sect. 2.3.1):
M
3
= i∂/∂α , K
3
= i∂/∂γ ,
1
2
e
iα
M
+
− e
−iα
M
−
=
1
2
e
−iγ
K
−
− e
iγ
K
+
=
∂
∂β
,
1
2
e
iα
M
+
+ e
−iα
M
−
=−
(
cot β
)
M
3
+
(
sin β
)
−1
K
3
,
1
2
e
−iγ
K
−
+ e
iγ
K
+
=
(
cot β
)
K
3
−
(
sin β
)
−1
M
3
,
M
+
= e
−ia
[∂/∂β −
(
cot β
)
M
3
+
(
sin β
)
−1
K
3
] ,
M
−
= e
iα
[−∂/∂β −
(
cot β
)
M
3
+
(
sin β
)
−1
K
3
] ,
K
+
= e
−iγ
[−∂/∂β +
(
cot β
)
K
3
−
(
sin β
)
−1
M
3
] ,
K
−
= e
iγ
[∂/∂β +
(
cot β
)
K
3
−
(
sin β
)
−1
M
3
] .
Euler angles with Z =U
∗
(αβγ) [replace i by −iinthe
above relations]:
M
3
=−i∂/∂α , K
3
=−i∂/∂γ , (2.34)
M
±
= e
±iα
#
±∂/∂β −(cot β)M
3
+(sin β)
−1
K
3
$
,
K
±
= e
±iγ
#
∓∂/∂β +(cot β)K
3
−(sin β)
−1
M
3
$
.
Since D
j
(U
∗
) = (D
j
(U))
∗
, which is denoted
D
j∗
(U), these operators have the standard action
on the complex conjugate functions D
j∗
mm
(U).
Quaternionic variables. (x
0
, x) ∈ R
4
:
x
0
,x
(x
0
, x) =
x
0
x
0
−x
·x, x
0
x+x
0
x
+x
× x
;
Z =
z
11
z
12
z
21
z
22
=
x
0
−ix
3
−ix
1
−x
2
−ix
1
+x
2
x
0
+ix
3
;
∂
∂Z
=
∂/∂z
11
∂/∂z
12
∂/∂z
21
∂/∂z
22
=
1
2
∂/∂x
0
+i∂/∂x
3
i∂/∂x
1
−∂/∂x
2
i∂/∂x
1
+∂/∂x
2
∂/∂x
0
−i∂/∂x
3
;
M
i
=
1
2
Tr
Z
T
σ
i
∂/∂Z
, K
i
=
1
2
Tr
σ
i
Z
T
∂/∂Z
.
(The form of ∂/∂Z is determined by the require-
ment (∂/∂z
ij
)z
lk
= δ
il
δ
jk
; for example,
1
2
(∂/∂x
0
+
i∂/∂x
3
)(x
0
−ix
3
) = 1).
Define the six orbital angular momentum operators
in R
4
by
L
jk
=−i(x
j
∂/∂x
k
−x
k
∂/∂x
j
), j < k = 0, 1, 2, 3 ,
which may be written as the orbital angular momentum
L in R
3
together with the three operators A given by
L =−ix× ∇ , L
1
= L
23
,
L
2
= L
31
, L
3
= L
12
,
A= (A
1
, A
2
, A
3
) = (L
01
, L
02
, L
03
).
Then, we have the following relations:
K
1
= (L
1
− A
1
)/2 , K
2
= (L
2
− A
2
)/2 ,
K
3
= (L
3
− A
3
)/2 ;
M
1
=−(L
1
+ A
1
)/2 , M
2
= (L
2
+ A
2
)/2 ,
M
3
=−(L
3
+ A
3
)/2 .
Part A 2.5

Angular Momentum Theory 2.6 The Symmetric Rotor and Representation Functions 29
Commutation rules:
[M
j
, K
k
]=0 , j, k =1, 2, 3 ,
M× M = iM , K × K = iK ,
L× L = iL , A× A= iL ,
[L
j
, A
k
]=ie
jkl
A
l
,
where e
jkl
= 1for j, k, l an even permutation of 1, 2, 3;
e
jkl
=−1 for an odd permutation of 1, 2, 3; e
jkl
= 0,
otherwise.
The M =(M
1
, M
2
, M
3
) and K = (K
1
, K
2
, K
3
) op-
erators have the standard action given in Sect. 2.2 on the
functions D
j
mm
(x
0
, x) defined by (2.22) (Replace α
0
by
x
0
and α by x). Additional relations:
K
2
= M
2
=−
1
4
R
2
∇
2
4
+K
2
0
+K
0
,
R
2
= x
2
0
+x·x ,
∇
2
4
=
∂
2
∂x
2
0
+∇
2
=
µ
∂
2
∂x
2
µ
,
K
0
=
1
2
Tr
z
T
∂
∂Z
=
1
2
3
µ=0
x
µ
∂
∂x
µ
;
K
0
D
j
mm
(x
0
, x) = jD
j
mm
(x
0
, x),
∇
2
4
D
j
mm
(x
0
, x) = 0 ;
(M
1
, −M
2
, M
3
) =
i
R
i1
K
i
,
i
R
i2
K
i
,
i
R
i3
K
i
,
R
ij
=
x
2
0
−x·x
δ
ij
−2e
ijk
x
0
x
k
+2x
i
x
j
x
2
0
+x·x
,
each (x
0
, x) ∈ R
4
.
The relation R
ij
= R
ij
(x
0
, x) is a mapping of all points
of four-space R
4
(except the origin) onto the group of
proper, orthogonal matrices; for x
2
0
+x·x = 1, it is just
the Euler–Rodrigues parametrization, (2.21).
The operators R = (−M
1
, M
2
, −M
3
) and K =
(K
1
, K
2
, K
3
) have the standard action on (−1)
j+m
D
j
−m,m
(x
0
, x), so that the orbital angular momentum in
R
3
is given by the addition L = R+K. Thus, one finds:
mm
C
jjL
mm
M
(−1)
j+m
D
j
−mm
(x
0
, x)
= A
2 j,L
R
2 j−L
Y
LM
(x)C
(L+1)
2 j−L
(x
0
/R),
A
2 j,L
= (2i)
L
(−1)
2 j
L!
4π(2 j −L)!
(2 j +L +1)!
1
2
.
2.6 The Symmetric Rotor and Representation Functions
The rigid rotor is an important physical object and its
quantum description enters into many physical theories.
This description is an application of angular momentum
theory with subtleties that need to be made explicit. It
is customary to describe the classical rotor in terms of
a right-handed triad of unit vectors
ˆ
f
1
,
ˆ
f
2
,
ˆ
f
3
fixed in
the rotor and constituting a principal axes system located
at the center of mass. The instantaneous orientation of
this body-fixed frame relative to a right-handed triad
of unit vector (
ˆ
e
1
,
ˆ
e
2
,
ˆ
e
3
) specifying an inertial frame,
also located at the center of mass, is then given, say, in
terms of Euler angles (one could use for this purpose
any parametrization of a proper, orthogonal matrix). For
Euler angles, the relationship is
ˆ
f
j
=
i
R
ij
(αβγ)
ˆ
e
i
. (2.35)
The Hamiltonian for the rigid rotor is then of the form
H = AP
2
1
+ BP
2
2
+CP
2
3
,
where A, B, and C are physical constants related to the
reciprocals of the principal moments of inertia, and the
angular momenta P
j
( j = 1, 2, 3) are the components of
the total angular momentum J referred to the body-fixed
frame:
P
j
=
ˆ
f
j
·J =
i
R
ij
(αβγ)J
i
,
J =
ˆ
e
1
J
1
+
ˆ
e
2
J
2
+
ˆ
e
3
J
3
.
For the symmetric rotor (taking A = B), the Hamiltonian
can be written in the form
H = aP
2
+bP
2
3
.
It is in the interpretation of this Hamiltonian for quan-
tum mechanics that the subtleties already enter, since
the nature of angular momentum components referred
to a moving reference system must be treated correctly.
Relation (2.35) shows that the body-fixed axes cannot
commute with the components of the total angular mo-
mentum J referred to the frame (
ˆ
e
1
,
ˆ
e
2
,
ˆ
e
3
). A position
Part A 2.6
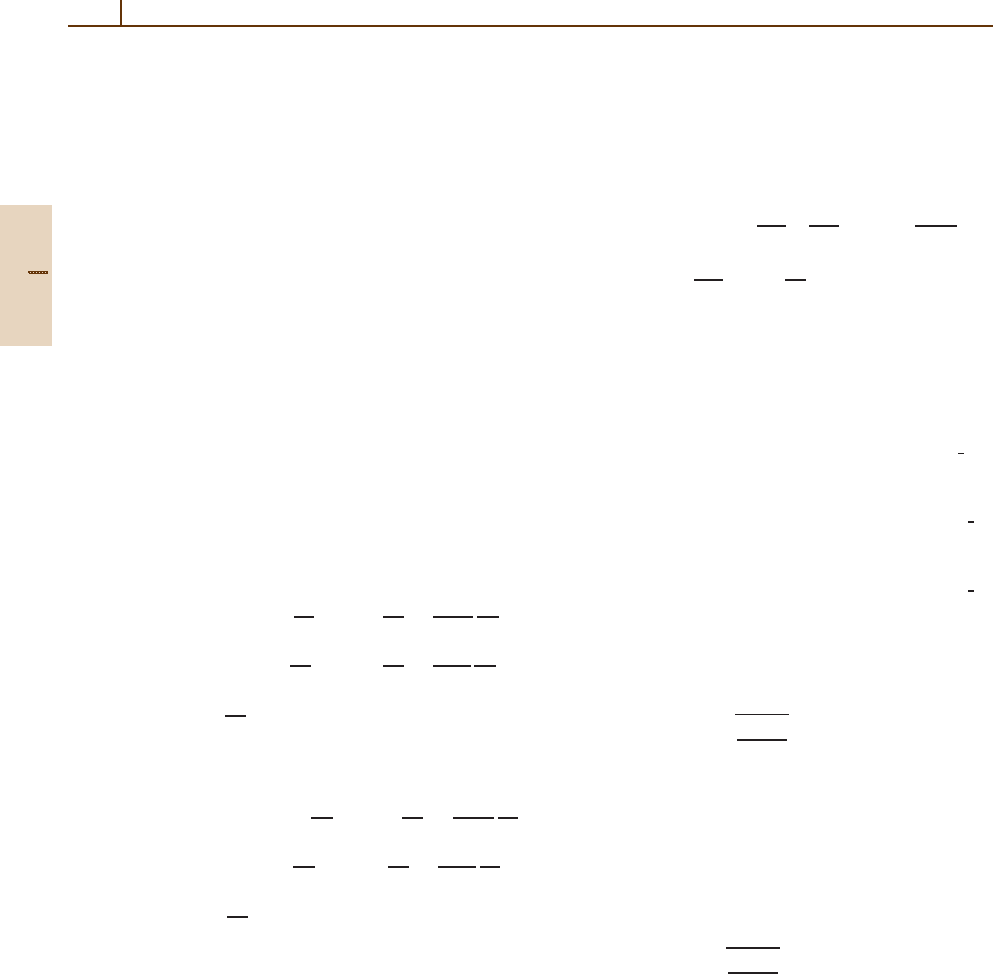
30 Part A Mathematical Methods
vector xand the orbital angular momentum L, with com-
ponents both referred to an inertial frame, satisfy the
commutation relations [L
j
, x
k
]=ie
jkl
x
l
, and for a rigid
body thought of as a collection of point particles rotating
together, the same conditions are to be enforced. Rela-
tive to the body-fixed frame, the vector x is expressed
as
k
x
k
ˆ
e
k
=
h
a
h
ˆ
f
h
, each a
h
= constant ,
x
k
=
h
a
h
R
kh
(αβγ) .
The direction cosines R
kh
= R
kh
(αβγ) =
ˆ
e
k
·
ˆ
f
h
and the
physical total angular momentum components referred
to an inertial frame must satisfy
!
J
j
, R
kh
"
= ie
jkl
R
lh
, each h = 1, 2, 3 ,
in complete analogy to [L
j
, x
k
]=ie
jkl
x
l
.
The description of the angular momentum associated
with a symmetric rigid rotor and the angular momentum
states is summarized as follows [compare (2.35)]:
Physical total angular momentum J with components
referred to (
ˆ
e
1
,
ˆ
e
2
,
ˆ
e
3
):
J
1
= icosα cot β
∂
∂α
+isinα
∂
∂β
−i
cos α
sin β
∂
∂γ
,
J
2
= isinα cot β
∂
∂α
−icosα
∂
∂β
−i
sin α
sin β
∂
∂γ
,
J
3
=−i
∂
∂α
.
Physical angular momentum J with components re-
ferred to
ˆ
f
1
,
ˆ
f
2
,
ˆ
f
3
:
P
1
=−icosγ cot β
∂
∂γ
−isinγ
∂
∂β
+i
cos γ
sin β
∂
∂α
,
P
2
= isinγ cot β
∂
∂γ
−icosγ
∂
∂β
−i
sin γ
sin β
∂
∂α
,
P
3
=−i
∂
∂γ
.
Standard commutation of the J
i
:
[J
i
, J
j
]=iJ
k
, i, j, k cyclic .
J
i
can stand to either side:
P
j
=
i
R
ij
(αβγ)J
i
, J
i
=
i
J
i
R
ij
(αβγ) .
The famous Van Vleck factor of −i in the commutation
of the P
i
:
[P
i
, P
j
]=−iP
k
, i, j, k cyclic .
Mutual commutativity of the J
j
and P
i
:
[P
i
, J
j
]=0 , i, j = 1, 2, 3 .
Same invariant (squared) total angular momentum:
P
2
1
+P
2
2
+P
2
3
= J
2
1
+J
2
2
+J
2
3
= J
2
=−csc
2
β
∂
2
∂α
2
+
∂
2
∂γ
2
−2cosβ
∂
2
∂α∂γ
−
∂
2
∂β
2
−cot β
∂
∂β
.
Standard actions:
J
2
D
j∗
mm
(αβγ) = j( j +1)D
j∗
mm
(αβγ) ,
J
3
D
j∗
mm
(αβγ) = mD
j∗
mm
(αβγ) ,
P
3
D
j∗
mm
(αβγ) = m
D
j∗
mm
(αβγ) ;
J
±
D
j∗
mm
(αβγ) =[( j ∓m)( j ±m +1)]
1
2
× D
j∗
m±1,m
(αβγ) ,
(P
1
−iP
2
)D
j∗
mm
(αβγ) =[( j −m
)( j +m
+1)]
1
2
× D
j∗
m,m
+1
(αβγ) ,
(P
1
+iP
2
)D
j∗
mm
(αβγ) =[( j +m
)( j −m
+1)]
1
2
× D
j∗
m,m
−1
(αβγ) .
Normalized wave functions:
Integral or half-integral j (SU(2) solid body):
*
αβγ
&
&
&
&
j
mm
+
=
,
2 j +1
2π
2
D
j∗
mm
(αβγ) , (2.36)
with inner product
F|F
=
dΩ αβγ |F
∗
αβγ |F
,
where dΩ is defined by (2.25) and the integration
extends over all α, β, γ givenby(2.26).
Integral j (collection of “rigid” point particles):
Ψ
j
mm
(αβγ) =
,
2 j +1
8π
2
D
j∗
mm
(αβγ) , (2.37)
with inner product
(Ψ, Ψ
) =
2π
0
dα
π
0
dβ sin β
2π
0
dγ F
∗
(αβγ)F
(αβγ) .
The concept of a solid (impenetrable) body is conceptu-
ally distinct from that of a collection of point particles
moving collectively together in translation and rotation.
Part A 2.6

Angular Momentum Theory 2.7 Wigner–Clebsch–Gordan and 3-j Coefficients 31
2.7 Wigner–Clebsch–Gordan and 3-j Coefficients
Wigner–Clebsch–Gordan (WCG) coefficients (also
called vector coupling coefficients) enter the theory
of angular momentum in several ways: (1) as the co-
efficients in the real, orthogonal matrix that reduces
the Kronecker product of two irreducible represen-
tations of the quantal rotation group into a direct
sum of irreducibles; (2) as the coupling coefficients
for constructing basis states of sharp angular momen-
tum in the tensor product space from basis states of
sharp angular momentum spanning the two constituent
spaces; (3) as purely combinatoric objects in the ex-
pansion of a power of a 3 × 3 determinant; and (4) as
coupling coefficients in the algebra of tensor opera-
tors. These perspectives are intimately connected, but
have a different focus: the first considers the group
itself to be primary and views the Lie algebra as
the secondary or derived concept; the second consid-
ers the Lie algebra and the construction of the vector
spaces that carry irreducible representations as pri-
mary, and views the representations carried by these
spaces as derived quantities; the third is a mathe-
matical construction, at first seeming almost empty
of angular momentum concepts, yet the most reveal-
ing in showing the symmetry and other properties
of the WCG-coefficients; and the fourth is the nat-
ural extension of (2) to operators, recognizing that
the set of mappings of a vector space into itself is
also a vector space. The subject of tensor opera-
tor algebra is considered in the next section because
of its special importance for physical applications.
This section summarizes formulas relating to the first
three viewpoints, giving also the explicit mathemat-
ical expression of the coefficients in their several
forms.
Either viewpoint, (1) or (2), may be taken as an
interpretation of the Clebsch–Gordan series, which ex-
presses abstractly the reduction of a Kronecker product
of matrices (denoted ×) into a direct sum (denoted ⊕)of
matrices:
[j
1
]× [j
2
]=
j
1
+j
2
j=|j
1
−j
2
|
⊕[j]
=[|j
1
− j
2
|]⊕[|j
1
− j
2
|+1]⊕···⊕[j
1
+ j
2
] .
(2.38)
Given two angular momenta j
1
∈{0,
1
2
, 1,...} and
j
2
∈{0,
1
2
, 1,...}, the Clebsch–Gordan (CG)series
also expresses the rule of addition of two angular
momenta:
j = j
1
+ j
2
, j
1
+ j
2
−1, ... , |j
1
− j
2
| .
The integers
j
1
j
2
j
defined by
j
1
j
2
j
=
1 , for j
1
, j
2
, j satisfying
the CG-series rule
0 , otherwise
,
(2.39)
are useful in many relations between angular momentum
quantities. The notation ( j
1
j
2
j) is used to symbolize the
CG-series relation between three angular momentum
quantum numbers.
The representation function and Lie algebra inter-
pretations of the CG-series (2.38) are, respectively:
C(D
j
1
× D
j
2
)C
T
=
j
⊕
j
1
j
2
j
D
j
,
C
J
( j
1
)
i
× J
( j
2
)
i
C
T
=
j
⊕
j
1
j
2
j
J
( j)
i
,
i = 1, 2, 3 .
The notation J
( j)
i
denotes the (2 j +1) × (2 j +1) matrix
with elements
J
( j)
m
,m
=jm
| J
i
| jm ,
m
, m = j, j −1,... ,−j .
The elements of the real, orthogonal matrix C of dimen-
sion (2 j
1
+1)(2 j
2
+1) that effects these reductions are
the WCG-coefficients:
(C)
jm;m
1
m
2
= C
j
1
j
2
j
m
1
m
2
m
.
The pairs, ( jm) and (m
1
m
2
), index rows and columns,
respectively, of the matrix C:
( jm) : j = j
1
+ j
2
,... ,|j
1
− j
2
| ,
m = j,... ,−j ;
(m
1
m
2
) : m
1
= j
1
,... ,−j
1
;
m
2
= j
2
,... ,−j
2
.
Sum rule on projection quantum numbers:
C
j
1
j
2
j
m
1
m
2
m
= 0 , for m
1
+m
2
= m . (2.40)
Clebsch–Gordan series rule on angular momentum
quantum numbers:
C
j
1
j
2
j
m
1
m
2
m
= 0 , for
j
1
j
2
j
= 0 . (2.41)
Part A 2.7
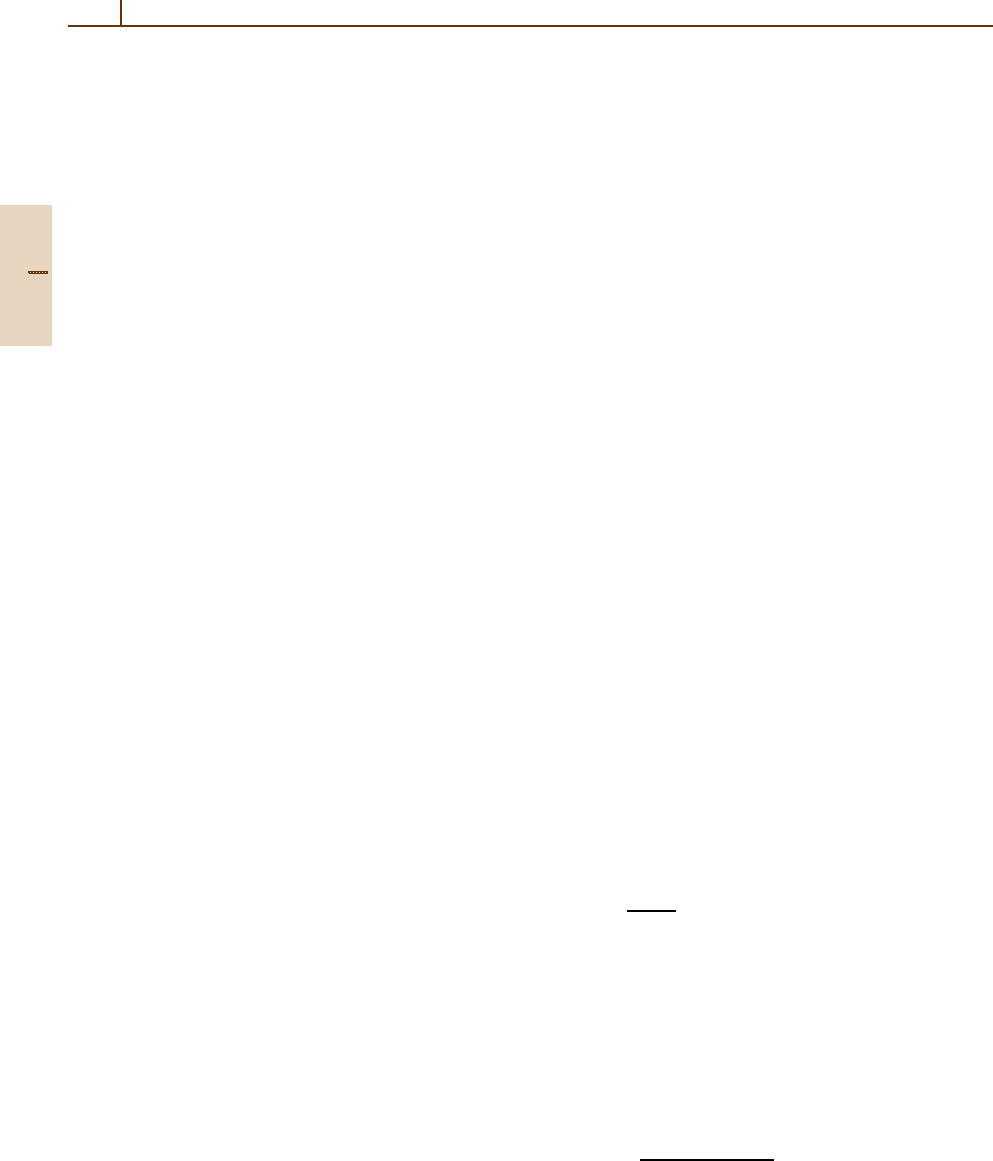
32 Part A Mathematical Methods
In presenting formulas that express relations relating
to the conceptual framework described above, it is best
to use a notation for a WCG-coefficient giving it as an
element of an orthogonal matrix. For the expression of
symmetry relations, the 3– j coefficient or 3– j symbol
notation is most convenient. The following notations are
used here:
WCG-coefficient notation:
|( j
1
j
2
) jm=
m
1
,m
2
C
j
1
j
2
j
m
1
m
2
m
|j
1
m
1
⊗|j
2
m
2
,
|j
1
m
1
; j
2
m
2
=|j
1
m
1
⊗|j
2
m
2
,
C
j
1
j
2
j
m
1
m
2
m
=j
1
m
1
; j
2
m
2
|( j
1
j
2
) jm ,
( j
1
j
2
) j
m
|( j
1
j
2
) jm=δ
j
j
δ
m
m
.
The 3– j coefficient notation:
j
1
j
2
j
m
1
m
2
−m
= (−1)
j
1
−j
2
+m
(2 j +1)
−1/2
C
j
1
j
2
j
m
1
m
2
m
. (2.42)
Orthogonality of WCG-coefficients:
Orthogonality of rows:
m
1
m
2
C
j
1
j
2
j
m
1
m
2
m
C
j
1
j
2
j
m
1
m
2
m
= δ
jj
δ
mm
. (2.43)
Orthogonality of columns (three forms):
jm
C
j
1
j
2
j
m
1
m
2
m
C
j
1
j
2
j
m
1
m
2
m
= δ
m
1
m
1
δ
m
2
m
2
,
j
C
j
1
j
2
j
m
1
m−m
1
,m
C
j
1
j
2
j
m
1
,m−m
1
,m
= δ
m
1
m
1
,
j
C
j
1
j
2
j
m−m
2
,m
2
,m
C
j
1
j
2
j
m−m
2
,m
2
,m
= δ
m
2
m
2
. (2.44)
Orthogonality of 3– j coefficients (symbols):
m
1
m
2
j
1
j
2
j
3
m
1
m
2
m
3
j
1
j
2
j
3
m
1
m
2
m
3
= δ
j
3
j
3
δ
m
3
m
3
/(2 j
3
+1), (2.45)
j
3
m
3
(2 j
3
+1)
j
1
j
2
j
3
m
1
m
2
m
3
j
1
j
2
j
3
m
1
m
2
m
3
= δ
m
1
m
1
δ
m
2
m
2
. (2.46)
The integers
j
1
j
2
j
( j
3
= j) are sometimes included
in the orthogonality relations (2.43)and(2.45)to
incorporate the extended definition (2.41)oftheWCG-
coefficients.
2.7.1 Kronecker Product Reduction
Product form:
D
j
1
m
1
m
1
(U)D
j
2
m
2
m
2
(U)
=
j
C
j
1
j
2
j
m
1
,m
2
,m
1
+m
2
C
j
1
j
2
j
m
1
,m
2
,m
1
+m
2
× D
j
m
1
+m
2
,m
1
+m
2
(U).
Singly coupled form:
m
1
+m
2
=m
C
j
1
j
2
j
m
1
m
2
m
D
j
1
m
1
m
1
(U)D
j
2
m
2
m
2
(U)
= C
j
1
j
2
j
m
1
,m
2
,m
1
+m
2
D
j
m
1
+m
2
,m
(U).
Doubly coupled (reduction) form:
m
1
+m
2
=m
m
1
+m
2
=m
C
j
1
j
2
j
m
1
m
2
m
C
j
1
j
2
j
m
1
m
2
m
D
j
1
m
1
m
1
(U)D
j
2
m
2
m
2
(U)
= δ
j
j
D
j
m
m
(U).
Integral relation:
dΩD
j
1
m
1
m
1
(U)D
j
2
m
2
m
2
(U)D
j
∗
m
m
1
(U)
=
2π
2
2 j +1
C
j
1
j
2
j
m
1
m
2
m
C
j
1
j
2
j
m
1
m
2
m
,
in any parametrization of U ∈ SU(2) that covers S
3
exactly once.
Gaunt’s integral:
2π
0
dα
π
0
sin β dβY
∗
lm
(βα)Y
l
1
m
1
(βα)Y
l
2
m
2
(βα)
=
(2l
1
+1)(2l
2
+1)
4π(2l+1)
1/2
C
l
1
l
2
l
000
C
l
1
l
2
l
m
1
m
2
m
.
Part A 2.7
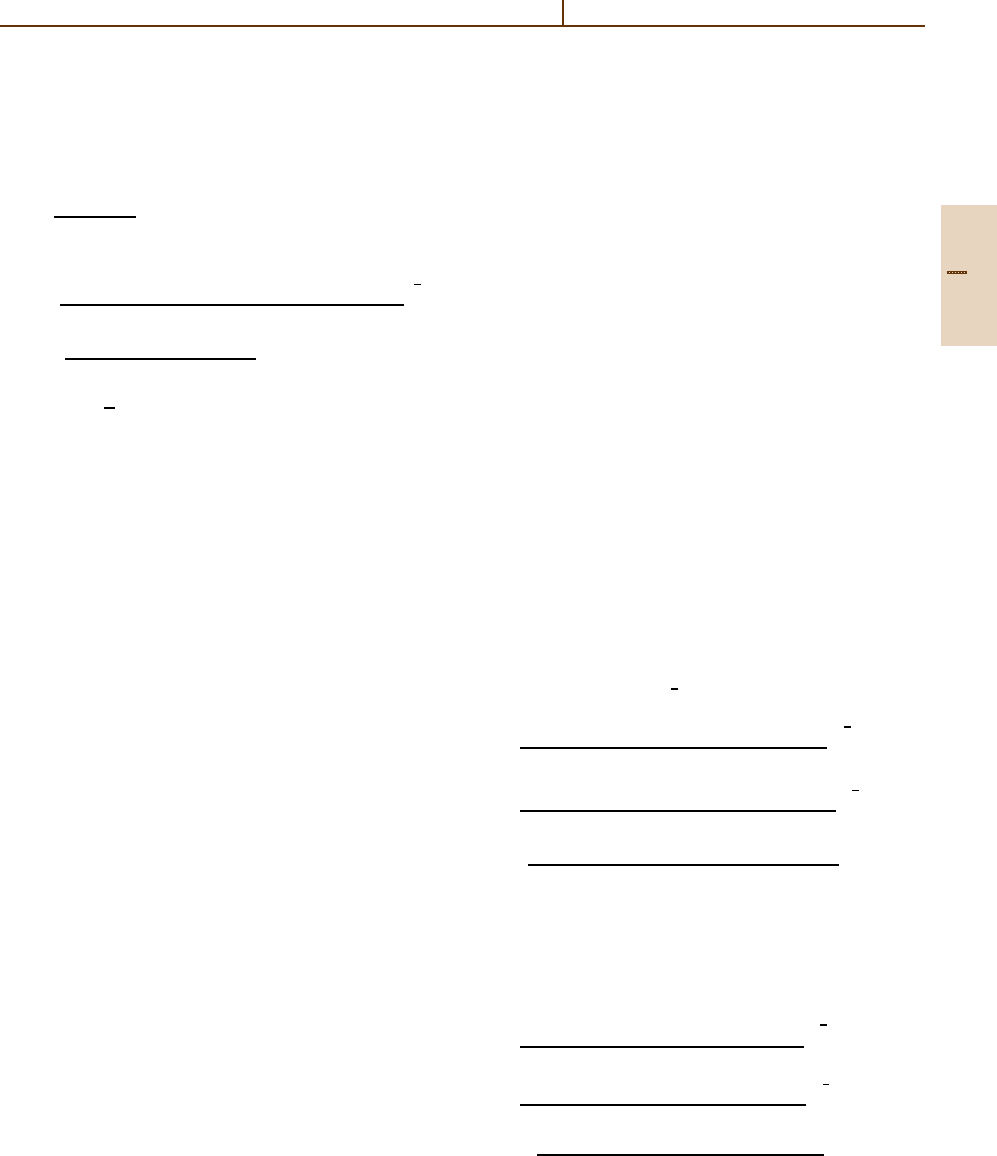
Angular Momentum Theory 2.7 Wigner–Clebsch–Gordan and 3-j Coefficients 33
Integral over three Legendre functions:
π
0
sin β dβP
l
(cos β) P
l
1
(cos β) P
l
2
(cos β)
=
2
C
l
1
l
2
l
000
2
2l+1
.
C
l
1
l
2
l
000
=
(2l+1)(l
1
+l
2
−l)!(l
1
−l
2
+l)!(−l
1
+l
2
+l)!
(l
1
+l
2
+l +1)!
1
2
×
(−1)
L−1
L!
(L −l
1
)!(L −l
2
)!(L −l)!
,
L =
1
2
(l
1
+l
2
+l),
for l
1
+l
2
+l even
C
l
1
l
2
l
000
= 0 , for l
1
+l
2
+l odd .
2.7.2 Tensor Product Space Construction
Orthonormal basis of H
j
1
:
(
|j
1
m
1
&
&
m
1
= j
1
, j
1
−1,... ,−j
1
)
.
Orthonormal basis of H
j
2
:
(
|j
2
m
2
&
&
m
2
= j
2
, j
2
−1,... ,−j
2
)
.
Uncoupled basis of H
j
1
⊗H
j
2
:
(
|j
1
m
1
⊗|j
2
m
2
&
&
m
1
= j
1
, j
1
−1,... ,−j
1
;
m
2
= j
2
, j
2
−1,... ,−j
2
)
.
Coupled basis of H
j
1
⊗H
j
2
:
(
|( j
1
j
2
) jm
&
&
j = j
1
+ j
2
, j
1
+ j
2
−1,... ,|j
1
− j
2
|;
m = j, j−1,... ,−j
)
,
|( j
1
j
2
) jm=
m
1
m
2
C
j
1
j
2
j
m
1
m
2
m
|j
1
m
1
⊗|j
2
m
2
.
Unitary transformations of spaces:
T
U
|j
1
m
1
=
m
1
D
j
1
m
1
m
1
(U)
&
&
j
1
m
1
-
,
m
1
= j
1
, j
1
−1,... ,−j
1
, each U ∈ SU(2) ;
T
V
|j
2
m
2
=
m
2
D
j
m
2
m
2
(V)
&
&
j
2
m
2
-
,
m
2
= j
2
, j
2
−1,... ,−j
2
, each V ∈ SU(2) ;
T
(U,V )
|j
1
m
1
⊗|j
2
m
2
=T
U
|j
1
m
1
⊗T
V
|j
2
m
2
=
m
1
m
2
D
j
1
m
1
m
1
(U)D
j
2
m
2
m
2
(V)
&
&
j
1
m
1
-
⊗
&
&
j
2
m
2
-
,
each U ∈ SU(2), each V ∈ SU(2) ;
T
(U,U)
|( j
1
j
2
) jm=
m
D
j
m
m
(U)|( j
1
j
2
) jm
,
m = j, j−1,... ,−j; each U ∈ SU(2).
Representation of direct product group SU(2) × SU(2):
T
(U,V )
T
(U
,V
)
= T
(UU
,VV
)
.
Representation of SU(2) as diagonal subgroup of
SU(2) × SU(2):
T
(U,U)
T
(U
,U
)
= T
(UU
,UU
)
,
T
U
= T
(U,U)
.
2.7.3 Explicit Forms of WCG-Coefficients
Wigner’s form:
C
j
1
j
2
j
m
1
m
2
m
= δ(m
1
+m
2
, m)(2 j +1)
1
2
×
( j + j
1
− j
2
)!( j − j
1
+ j
2
)!( j
1
+ j
2
− j)!
( j + j
1
+ j
2
+1)!
1
2
×
( j +m)!( j −m)!
( j
1
+m
1
)!( j
1
−m
1
)!( j
2
+m
2
)!( j
2
−m
2
)!
1
2
×
s
(−1)
j
2
+m
2
+s
( j
2
+ j+m
1
−s)!( j
1
−m
1
+s)!
s!( j − j
1
+ j
2
−s)!( j +m −s)!( j
1
− j
2
−m +s)!
.
Racah’s form:
C
j
1
j
2
j
m
1
m
2
m
=
δ(m
1
+m
2
, m)
×
(2 j +1)( j
1
+ j
2
− j)!
( j
1
+ j
2
+ j+1)!( j + j
1
− j
2
)!( j + j
2
− j
1
)!
1
2
×
( j
1
−m
1
)!( j
2
−m
2
)!( j −m)!( j +m)!
( j
1
+m
1
)!( j
2
+m
2
)!
1
2
×
t
(−1)
j
1
−m
1
+t
( j
1
+m
1
+t)!( j + j
2
−m
1
−t)!
t!( j −m −t)!( j
1
−m
1
−t)!( j
2
− j+m
1
+t)!
.
Part A 2.7
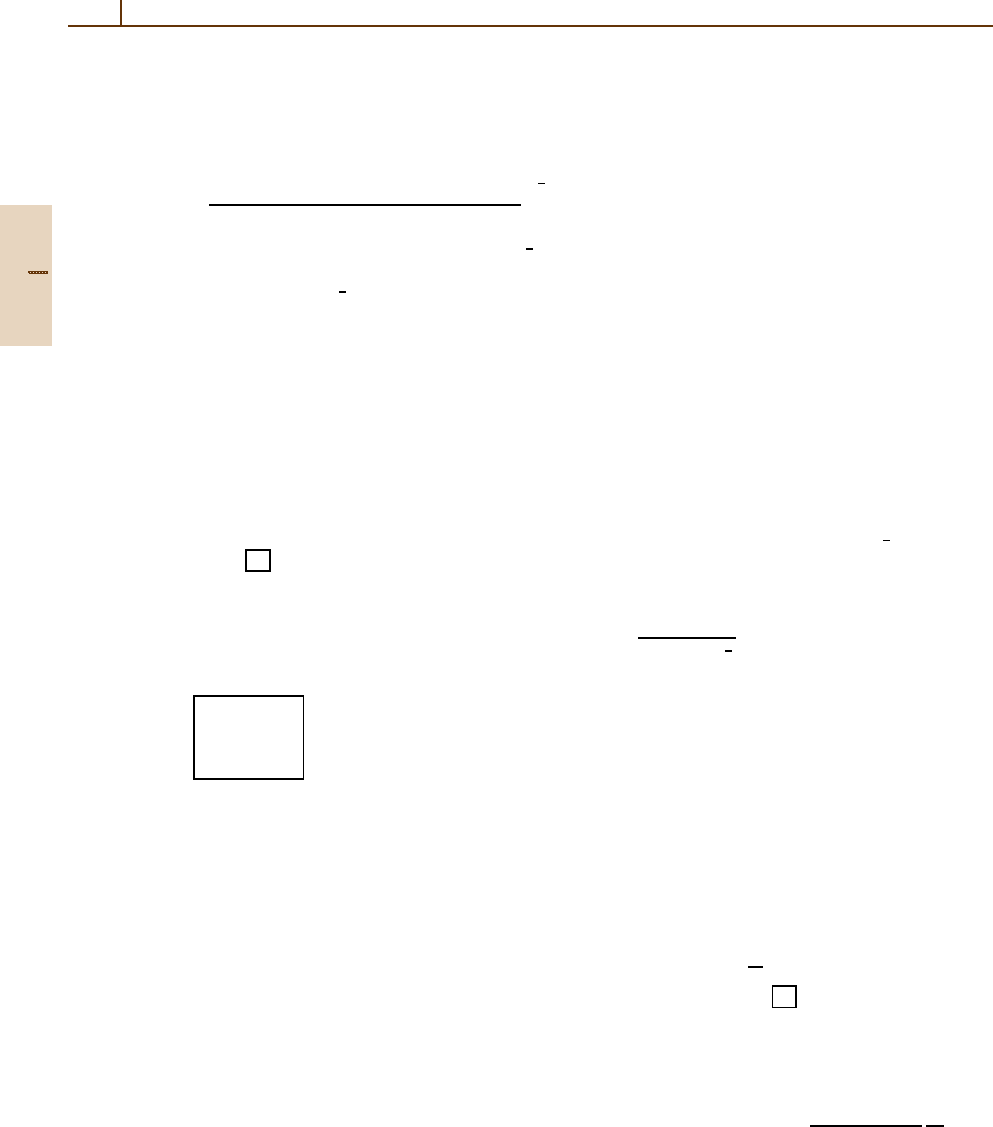
34 Part A Mathematical Methods
Van der Waerden’s form:
C
j
1
j
2
j
m
1
m
2
m
= δ(m
1
+m
2
, m)
×
(2 j +1)( j
1
+ j
2
− j)!( j + j
1
− j
2
)!( j + j
2
− j
1
)!
( j
1
+ j
2
+ j +1)!
1
2
×
!
( j
1
+m
1
)!( j
1
−m
1
)!( j
2
+m
2
)!( j
2
−m
2
)!
"
1
2
×
!
( j +m)!( j −m)!
"
1
2
×
k
(−1)
k
!
k !( j
1
+ j
2
− j −k)!( j
1
−m
1
−k)!
× ( j
2
+m
2
−k)!( j − j
2
+m
1
+k)!
× ( j − j
1
−m
2
+k)!
"
−1
Regge’s formula and its combinatoric structure:
(det A)
k
=
α
A(α)
3
i, j=1
(a
ij
)
α
ij
, A =(a
ij
),
(2.47)
where the summation is over all nonnegative integers α
ij
that satisfy the row and column sum constraints (2.17)
given by
α =
α
11
α
12
α
13
α
21
α
22
α
23
α
31
α
32
α
33
k
k
k
kkk
(2.48)
The coefficients A(α) are constrained sums over multi-
nomial coefficients:
A(α) =
(−1)
φ(K)
×
k
k
123
, k
132
, k
231
, k
213
, k
312
, k
321
,
where the summation is carried out over all nonnegative
integers k
i
1
i
2
i
3
such that
α
11
= k
123
+k
132
,α
12
= k
231
+k
213
,
α
13
= k
312
+k
321
,
α
21
= k
312
+k
213
,α
22
= k
123
+k
321
,
α
23
= k
231
+k
132
,
α
31
= k
231
+k
321
,α
32
= k
312
+k
132
,
α
33
= k
123
+k
213
,
φ(K) =
π∈A
3
k
π
= k
132
+k
213
+k
321
.
The general multinomial coefficient is the integer de-
fined by
k
k
1
, k
2
,... ,k
s
= k!/k
1
!k
2
!···k
s
! , k =
i
k
i
.
Relation (2.47) generalizes in the obvious way to an
n × n determinant, using the symmetric group S
n
and
its S
n−1
subgroups S
( j)
n−1
,where j denotes that this is
the permutation group on the integers 1, 2,... ,n with
j deleted [2.2].
Regge’s formula for the 3– j coefficient is:
j
1
j
2
j
3
m
1
m
2
m
3
= δ(m
1
+m
2
+m
3
, 0)
3
i, j=1
(α
ij
)!
1
2
×
A(α)
k ![(k+1)!]
1
2
,
k = j
1
+ j
2
+ j
3
, (2.49)
α
11
= j
1
+m
1
,α
12
= j
2
+m
2
,α
13
= j
3
+m
3
,
α
21
= j
1
−m
1
,α
22
= j
2
−m
2
,α
23
= j
3
−m
3
,
α
31
= j
2
+ j
3
− j
1
,α
32
= j
3
+ j
1
− j
2
,
α
33
= j
1
+ j
2
− j
3
.
Equation (2.49)showsthatWCG-coefficients and
3– j coefficients are sums over integers, except for a mul-
tiplicative normalization factor.
Schwinger’s generating function:
exp(t det A) =
k
t
k
k !
α
A(α)
i, j
(a
ij
)
α
ij
.
The general definition of the
p
F
q
hypergeometric
function depending on p numerator parameters, q de-
nominator parameters, and a single variable z is:
p
F
q
a
1
... ,a
p
b
1
... ,b
q
;z
=
∞
n=0
(a
1
)
n
···(a
p
)
n
(b
1
)
n
···(b
q
)
n
z
n
n!
,
(a)
n
= a(a+1) ···(a+n −1), (a)
0
= 1 .
Part A 2.7
Angular Momentum Theory 2.7 Wigner–Clebsch–Gordan and 3-j Coefficients 35
Such a series is terminating if at least one of the nu-
merator parameters is a negative integer (and all other
factors are well-defined). Both WCG-coefficients and
Racah 6– j coefficients relate to special series of this
type, evaluated at z = 1. For WCG-coefficients, we have
for α +β =γ :
C
abc
αβγ
=
[
(2c+1)(a+α)!(a−α)!(b+β)!(b−β)!(c+γ)!
× (c−γ)!
]
1
2
(−1)
a+b+γ +δ
1
∆(abc)
×
3
F
2
1
−δ
1
,
2
−δ
1
,
3
−δ
1
δ
2
−δ
1
+1,δ
3
−δ
1
+1
;1
(δ
2
−δ
1
)!(δ
3
−δ
1
)!(δ
1
−
1
)!(δ
1
−
2
)!(δ
1
−
3
)!
,
δ
1
= min(a +α +b+β, b −β +c+γ, a +α +c+γ),
(δ
1
,δ
2
,δ
3
) = any permutation of (a+α +b+β, b−β
+c+γ, a+α +c+γ),afterδ
1
is fixed, (
1
,
2
,
3
) =
any permutation of (a+α, b+α +γ, c+γ).Asome-
what better form can be found in [2.2].
The quantity
∆(abc) =
(a+b−c)!(a−b+c)!(−a+b+c)!
(a+b+c+1)!
1
2
.
is called a triangle coefficient.
All 72 Regge symmetries are consequences of
known properties of the
3
F
2
hypergeometric series.
2.7.4 Symmetries of WCG-Coefficients
in 3-j Symbol Form
There are 72 known symmetries (up to sign changes)
of the 3– j coefficient. There are at least four ways
of verifying these symmetries: (1) directly from the
van der Waerden form of the coefficients; (2) di-
rectly from Regge’s generating function; (3) from
the known symmetries of the
3
F
2
hypergeomet-
ric series; and (4) directly from the symmetries of
the representation functions D
j
mm
(U).Thesetof
72 symmetries is succinctly expressed in terms of the
coefficient A(α) defined in Sect. 2.8.3 with α
ij
en-
tries given by (2.48)and(2.49)inwhichm
1
+m
2
+
m
3
= 0:
A
j
1
+m
1
j
2
+m
2
j
3
+m
3
j
1
−m
1
j
2
−m
2
j
3
−m
3
j
2
+ j
3
− j
1
j
3
+ j
1
− j
2
j
1
+ j
2
− j
3
.
This coefficient has determinantal symmetry; that
is, it is invariant under even permutations of its
rows or columns and under transposition, and is
multiplied by the factor (−1)
j
1
+j
2
+j
3
under odd
permutations of its rows or columns. These 72 deter-
minantal operations may be generated from the three
operations C
12
, C
13
, T consisting of interchange of
columns 1 and 2, interchange of columns 1 and 3,
and transposition, since the first two operations
generate the symmetric group S
3
of permutations
of columns, and the symmetric group S
3
of per-
mutations of rows is then given by TS
3
T.The
transposition T itself generates a group {e, T} iso-
morphic to the symmetric group S
2
. Thus, the
72 element determinantal group is the direct prod-
uct group S
3
× S
3
× {e, T}. The three relations between
3– j coefficients corresponding to the generators
C
12
, C
13
, T are
j
1
j
2
j
3
m
1
m
2
m
3
= (−1)
j
1
+j
2
+j
3
j
2
j
1
j
3
m
2
m
1
m
3
,
j
1
j
2
j
3
m
1
m
2
m
3
= (−1)
j
1
+j
2
+j
3
j
3
j
2
j
1
m
3
m
2
m
1
,
j
1
j
2
j
3
m
1
m
2
m
3
=
j
1
+j
2
+m
1
+m
2
2
j
1
+j
2
−m
1
−m
2
2
j
3
j
1
−j
2
+m
1
−m
2
2
j
1
−j
2
−m
1
+m
2
2
j
2
− j
1
.
All 72 relations among 3– j coefficients can be ob-
tained from these 3. The 12 “classical” symmetries of
the 3– j symbol
abc
αβγ
are expressed by:
1. even permutations of the columns leave the coeffi-
cient invariant;
2. odd permutations of the columns change the sign by
the factor (−1)
a+b+c
;
3. simultaneous sign reversal of the projection quantum
numbers changes the sign by (−1)
a+b+c
.
The 72 corresponding symmetries of the WCG-
coefficients (up to sign changes and dimensional factors)
are best obtained from those of the 3 j-coefficients by
using (2.42).
Part A 2.7

36 Part A Mathematical Methods
2.7.5 Recurrence Relations
Three-term:
[(J +1)( J −2 j
1
)]
1
2
j
1
j
2
j
3
m
1
m
2
m
3
=[( j
2
+m
2
)( j
3
−m
3
)]
1
2
j
1
j
2
−
1
2
j
3
−
1
2
m
1
m
2
−
1
2
m
3
+
1
2
−[( j
2
−m
2
)( j
3
+m
3
)]
1
2
j
1
j
2
−
1
2
j
3
−
1
2
m
1
m
2
+
1
2
m
3
−
1
2
;
[(J −2 j
2
)(J +1 −2 j
3
)]
1
2
j
1
j
2
j
3
m
1
m
2
m
3
+[( j
2
+m
2
+1)( j
3
+m
3
)]
1
2
×
j
1
j
2
−
1
2
j
3
+
1
2
m
1
m
2
−
1
2
m
3
+
1
2
+[( j
2
−m
2
+1)( j
3
−m
3
)]
1
2
×
j
1
j
2
−
1
2
j
3
+
1
2
m
1
m
2
+
1
2
m
3
−
1
2
= 0 ;
( j
2
+m
2
)
1
2
j
1
j
2
j
3
m
1
mm
3
=[( j
3
− j
1
+ j
2
)(J +1)( j
3
−m
3
)]
1
2
×
j
1
j
2
−
1
2
j
3
−
1
2
m
1
m
2
−
1
2
m
3
−
1
2
−[( j
1
− j
3
+ j
2
)(J −2 j
2
+1)( j
3
+m
3
+1)]
1
2
×
j
1
j
2
−
1
2
j
3
+
1
2
m
1
m
2
−
1
2
m
3
+
1
2
;
j
1
j
2
j
3
j
2
−m
3
−j
2
m
3
=−
2 j
2
( j
3
+m
3
)
( j
3
− j
1
+ j
2
)(J +1)
1
2
×
j
1
j
2
−
1
2
j
3
−
1
2
j
2
−m
3
−j
2
+
1
2
m
3
−
1
2
,
j
3
= j
1
+ j
2
, j
1
+ j
2
−1,... , j
1
− j
2
+1
for j
1
≥ j
2
;
j
1
j
2
j
3
j
2
−m
3
−j
2
m
3
=−
2 j
2
( j
3
−m
3
+1)
( j
1
− j
3
+ j
2
)(J −2 j
2
+1)
1
2
×
j
1
j
2
−
1
2
j
3
+
1
2
j
2
−m
3
−j
2
+
1
2
m
3
−
1
2
,
j
3
= j
1
+ j
2
−1, j
1
+ j
2
−2,... , j
1
− j
2
for j
1
≥ j
2
.
Four-term:
[(J+1)(J−2 j
1
)(J−2 j
2
)(J−2 j
3
+1)]
1
2
×
j
1
j
2
j
3
m
1
m
2
m
3
=
[
( j
2
−m
2
)( j
2
+m
2
+1)
× ( j
3
+m
3
)( j
3
+m
3
−1)]
1
2
×
j
1
j
2
j
3
−1
m
1
m
2
+1 m
3
−1
−2m
2
[( j
3
+m
3
)( j
3
−m
3
)]
1
2
j
1
j
2
j
3
−1
m
1
m
2
m
3
−[( j
2
+m
2
)( j
2
−m
2
+1)( j
3
−m
3
)( j
3
−m
3
−1)]
1
2
×
j
1
j
2
j
3
−1
m
1
m
2
−1 m
3
+1
.
Five-term:
C
bd f
β,δ,β+δ
=
(b+d−f )(b+f−d+1)(d−δ)( f+β+δ+1)
(2d)(2 f+1)(2d)(2 f+2)
1
2
× C
bd−1/2 f+1/2
β,δ+1/2,β+δ+1/2
−
(b+d−f )(b+f−d+1)(d+δ)( f−β−δ+1)
(2d)(2 f+1)(2d)(2 f+2)
1
2
× C
bd−1/2 f+1/2
β,δ−1/2,β+δ−1/2
+
(d+f−b)(b+d+f+1)(d+δ)( f+β+δ)
(2d)(2 f+1)(2d)(2 f )
1
2
× C
bd−1/2 f−1/2
β,δ−1/2,β+δ−1/2
+
(d+f−b)(b+d+f+1)(d−δ)( f−β−δ)
(2d)(2 f+1)(2d)(2 f )
1
2
× C
bd−1/2 f−1/2
β,δ+1/2,β+δ+1/2
.
Part A 2.7
Angular Momentum Theory 2.8 Tensor Operator Algebra 37
This relation may be used to prove the limit rela-
tion (2.50) from the similar recurrence relation (2.84c)
for the Racah coefficients.
2.7.6 Limiting Properties
and Asymptotic Forms
lim
a→∞
C
aba+ρ
a−α,β,a−α+β
= δ
ρβ
,
lim
j→∞
(−1)
a+b+2 j−τ
[(2c+1)(2 j −2σ +1)]
1
2
×
j −τ aj−σ
bjc
= C
abc
ρστ
, (2.50)
where the brace symbol is a 6– j coefficient (Sect. 2.9).
C
jk j+∆
m,µ,m+µ
≈ (−1)
∆−µ
D
k
µ∆
cos
1
2
β sin
1
2
β
−sin
1
2
β cos
1
2
β
= d
k
µ∆
(β) , for large j ;
cos
1
2
β =
2
j +m
2 j
, sin
1
2
β =
2
j −m
2 j
,
C
jk j
m0m
≈ P
k
(cos β) , for large j ;
(−1)
k
[(2 j +1)(2J +1)]
1
2
W( j, k, J +m, J; j, J)
∼ P
k
(cos β),
first for large J, then large j (Sect. 2.9).
2.7.7 WCG-Coefficients as Discretized
Representation Functions
C
j
1
j
2
j
m
1
m
2
m
= δ
m
1
+m
2
,m
(−1)
j
1
−m
1
×
(2 j +1)( j
1
+ j
2
− j)!
( j
1
+ j
2
+ j +1)!
1
2
× D
j
m, j
1
−j
2
√
j
1
+m
1
√
j
2
+m
2
−
√
j
1
−m
1
√
j
2
−m
2
symbolic
powers
,
(2.51)
where in evaluating this result one first substitutes
u
11
=
3
j
1
+m
1
,
u
12
=
3
j
2
+m
2
,
u
21
=−
3
j
1
−m
1
,
u
22
=
3
j
2
−m
2
into the form (2.17), followed by the replacement of
ordinary powers by generalized powers:
(±
√
k)
s
→ (±1)
s
k !
(k−s)!
1
2
.
2.8 Tensor Operator Algebra
2.8.1 Conceptual Framework
A tensor operator can be characterized in terms of its
algebraic properties with respect to the angular momen-
tum J or in terms of its transformation properties under
unitary transformations generated by J. Both viewpoints
are essential.
A tensor operator T with respect to the group SU(2)
is a set of linear operators
T ={T
1
, T
2
,... ,T
n
} ,
where each operator in the set acts in the space H
defined by (2.10) and maps this space into itself
T
i
: H → H, i =1, 2,... ,n, and where this set of op-
erators has the following properties with respect to the
angular momentum J, which acts in the same space H
in the standard way:
1. Commutation relations with respect to the angular
momentum J:
[J
i
, T
j
]=
n
k=1
t
(i)
kj
T
k
,
where the t
(i)
kj
are scalars (invariants) with respect
to J.
2. Unitary transformation with respect to SU(2) rota-
tions:
e
−iψ
ˆ
n·J
T
i
e
iψ
ˆ
n·J
=
n
j=1
D
ji
(U)T
j
,
U =U(ψ,
ˆ
n),
where the matrix D(U) is an n × n unitary matrix rep-
resentation of SU(2). Reduction of this representation
into its irreducible constituents gives the notion of an ir-
Part A 2.8
