Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics
Подождите немного. Документ загружается.


7
Mathemati
Part A
Part A Mathematical Methods
2 Angular Momentum Theory
James D. Louck, Los Alamos, USA
3 Group Theory for Atomic Shells
Brian R. Judd, Baltimore, USA
4 Dynamical Groups
Josef Paldus, Waterloo, Canada
5 Perturbation Theory
Josef Paldus, Waterloo, Canada
6 Second Quantization
Brian R. Judd, Baltimore, USA
7 Density Matrices
Klaus Bartschat, Des Moines, USA
8 Computational Techniques
David R. Schultz, Oak Ridge, USA
Michael R. Strayer, Oak Ridge, USA
9 Hydrogenic Wave Functions
Robert N. Hill, Saint Paul, USA

9
Angular Mome
2. Angular Momentum Theory
Angular momentum theory is presented from the
viewpoint of the group SU(1) of unimodular unitary
matrices of order two. This is the basic quantum
mechanical rotation group for implementing the
consequences of rotational symmetry into isolated
complex physical systems, and gives the structure
of the angular momentum multiplets of such
systems. This entails the study of representation
functions of SU(2), the Lie algebra of SU(2) and
copies thereof, and the associated Wigner–
Clebsch–Gordan coefficients, Racah coefficients,
and 1n–j coefficients, with an almost boundless
set of inter-relations, and presentations of the
associated conceptual framework. The relationship
to the rotation group in physical 3-space is
given in detail. Formulas are often given in
a compendium format with brief introductions
on their physical and mathematical content.
A special effort is made to inter-relate the
material to the special functions of mathematics
and to the combinatorial foundations of the
subject.
2.1 Orbital Angular Momentum .................. 12
2.1.1 Cartesian Representation ........... 12
2.1.2 Spherical Polar Coordinate
Representation ......................... 15
2.2 Abstract Angular Momentum ................ 16
2.3 Representation Functions..................... 18
2.3.1 Parametrizations
of the Groups SU(2) and SO(3,R)... 18
2.3.2 Explicit Forms
of Representation Functions ....... 19
2.3.3 Relations to Special Functions..... 21
2.3.4 Orthogonality Properties ............ 21
2.3.5 Recurrence Relations ................. 22
2.3.6 Symmetry Relations................... 23
2.4 Group and Lie Algebra Actions .............. 25
2.4.1 Matrix Group Actions ................. 25
2.4.2 Lie Algebra Actions .................... 26
2.4.3 Hilbert Spaces ........................... 26
2.4.4 Relation
to Angular Momentum Theory..... 26
2.5 Differential Operator Realizations
of Angular Momentum ......................... 28
2.6 The Symmetric Rotor
and Representation Functions .............. 29
2.7 Wigner–Clebsch–Gordan
and 3-j Coefficients ............................. 31
2.7.1 Kronecker Product Reduction...... 32
2.7.2 Tensor Product Space
Construction ............................. 33
2.7.3 Explicit Forms
of WCG-Coefficients ................... 33
2.7.4 Symmetries of WCG-Coefficients
in 3-j Symbol Form ................... 35
2.7.5 Recurrence Relations ................. 36
2.7.6 Limiting Properties
and Asymptotic Forms ............... 36
2.7.7 WCG-Coefficients as Discretized
Representation Functions........... 37
2.8 Tensor Operator Algebra....................... 37
2.8.1 Conceptual Framework .............. 37
2.8.2 Universal Enveloping Algebra
of J ......................................... 38
2.8.3 Algebra
of Irreducible Tensor Operators ... 39
2.8.4 Wigner–Eckart Theorem ............. 39
2.8.5 Unit Tensor Operators
or Wigner Operators................... 40
2.9 Racah Coefficients ............................... 43
2.9.1 Basic Relations Between WCG
and Racah Coefficients............... 43
2.9.2 Orthogonality and Explicit Form .. 43
2.9.3 The Fundamental Identities
Between Racah Coefficients ........ 44
2.9.4 Schwinger–Bargmann
Generating Function
and its Combinatorics ................ 44
2.9.5 Symmetries of 6–j Coefficients.... 45
2.9.6 Further Properties ..................... 46
2.10 The 9–j Coefficients ............................. 47
2.10.1 Hilbert Space
and Tensor Operator Actions ....... 47
2.10.2 9–j Invariant Operators ............. 47
2.10.3 Basic Relations Between 9–j
Coefficients and 6–j Coefficients . 48
Part A 2
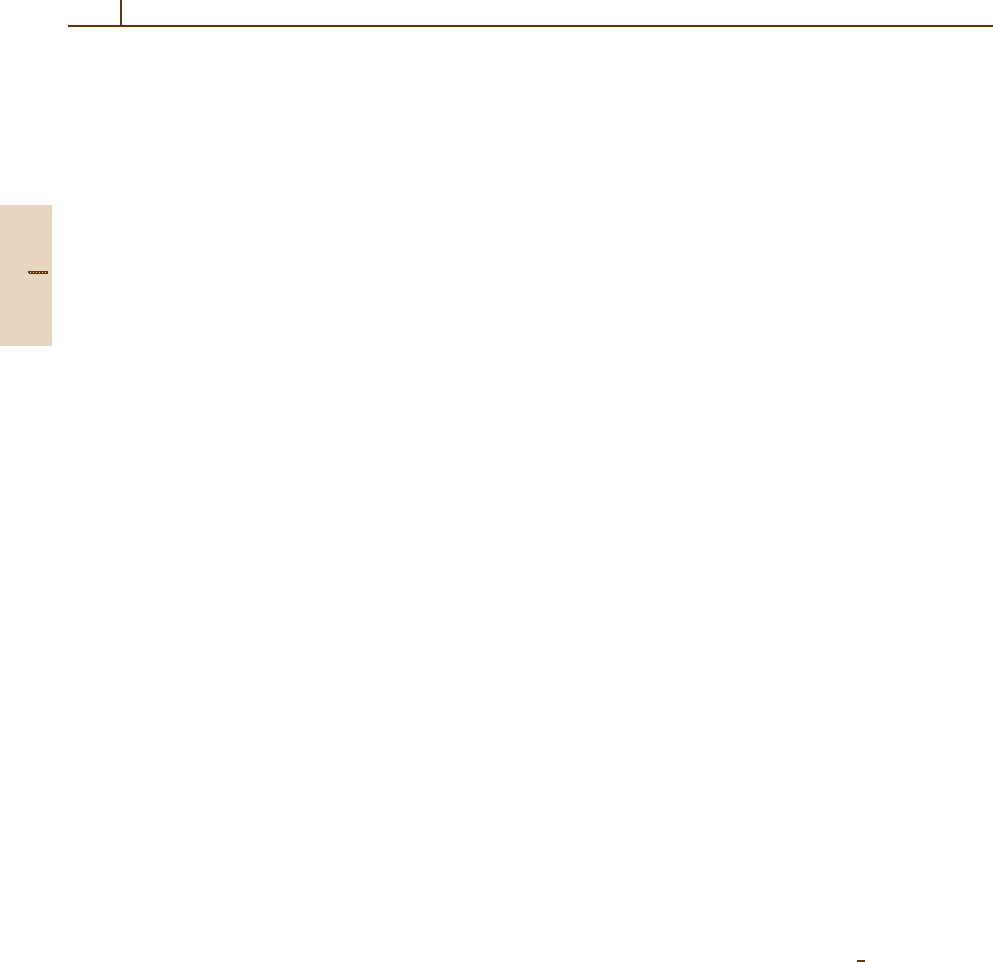
10 Part A Mathematical Methods
2.10.4 Symmetry Relations
for 9–j Coefficients
and Reductionto 6–j Coefficients 49
2.10.5 Explicit Algebraic Form
of 9–j Coefficients ..................... 49
2.10.6 Racah Operators........................ 49
2.10.7 Schwinger–Wu
Generating Function
and its Combinatorics ................ 51
2.11 Tensor Spherical Harmonics .................. 52
2.11.1 Spinor Spherical Harmonics
as Matrix Functions ................... 53
2.11.2 Vector Spherical Harmonics
as Matrix Functions ................... 53
2.11.3 Vector Solid Harmonics
as Vector Functions ................... 53
2.12 Coupling and Recoupling Theory
and 3n–j Coefficients........................... 54
2.12.1 Composite Angular Momentum
Systems ................................... 54
2.12.2 Binary Coupling Theory:
Combinatorics........................... 56
Angular momentum theory in its quantum mechani-
cal applications, which is the subject of this section,
is the study of the group of 2 × 2 unitary unimodular
matrices and its irreducible representations. It is the
mathematics of implementing into physical theory the
basic tenet that isolated physical systems are invariant to
rotations of the system in physical 3-space, denoted R
3
,
or, equivalently, to the orientation of a Cartesian ref-
erence system used to describe the system. That it is
the group of 2 × 2 unimodular matrices that is basic
in quantum theory in place of the more obvious group
of 3 × 3 real, orthogonal matrices representing transfor-
mations of the coordinates of the constituent particles
of the system, or of the reference frame, is a conse-
quence of the Hilbert space structure of the state space
of quantum systems and the impossibility of assigning
overall phase factors to such states because measure-
ments depend only on the absolute value of transition
amplitudes.
The exact relationship between the group SU(2)
of 2 × 2 unimodular unitary matrices and the group
SO(3, R) of 3 × 3 real, proper, orthogonal matrices is
an important one for keeping the quantum theory of an-
gular momentum, with its numerous conventions and
widespread applications across all fields of quantum
2.12.3 Implementation
of Binary Couplings ................... 57
2.12.4 Construction
of all Transformation Coefficients
in Binary Coupling Theory .......... 58
2.12.5 Unsolved Problems
in Recoupling Theory ................. 59
2.13 Supplement on Combinatorial
Foundations........................................ 60
2.13.1 SU(2) Solid Harmonics................ 60
2.13.2 Combinatorial Definition
of Wigner–Clebsch–Gordan
Coefficients .............................. 61
2.13.3 Magic Square Realization
of the Addition
of Two Angular Momenta ........... 63
2.13.4 MacMahon’s and Schwinger’s
Master Theorems....................... 64
2.13.5 The Pfaffian and Double Pfaffian. 65
2.13.6 Generating Functions
for Coupled Wave Functions
and Recoupling Coefficients ....... 66
2.14 Tables ................................................ 69
References .................................................. 72
physics, free of ambiguities. These notations and re-
lations are fixed at the outset.
Presentation of a point in R
3
:
x = col (x
1
, x
2
, x
3
) column matrix ,
x
T
= (x
1
, x
2
, x
3
) row matrix ,
X =
x
3
x
1
−ix
2
x
1
+ix
2
−x
3
2 × 2 traceless Hermitian matrix ;
Cartan’s representation .
A one-to-one correspondence between the set R
3
of
points in 3-space and the set H
2
of 2 × 2 traceless Her-
mitian matrices is obtained from x
i
=
1
2
Tr (σ
i
X),where
the σ
i
denote the matrices (Pauli matrices)
σ
1
=
01
10
,σ
2
=
0 −i
i0
,σ
3
=
10
0 −1
.
(2.1)
Mappings of R
3
onto itself:
x → x
= Rx ,
X → X
=UXU
†
,
Part A 2

Angular Momentum Theory 11
where † denotes Hermitian conjugation of a matrix or
an operator.
Two-to-one homomorphism of SU(2) onto SO(3, R):
R
ij
= R
ij
(U) =
1
2
Tr
σ
i
Uσ
j
U
†
,
(2.2)
ξ
x
=
10 0 0
0
0 R(U)
0
=
ξ
x
= A
†
(U × U
∗
)A
ξ
x
,
(2.3)
where ξ is an indeterminate, A is the unitary matrix
given by
A =
1
√
2
10 0 1
01−i0
01 i 0
10 0−1
,
U ×U
∗
denotes the matrix direct product, and ∗ denotes
complex conjugation. There is a simple unifying theme
in almost all the applications. The basic mathematical
notions that are implemented over and over again in
various contexts are: group action on the underlying
coordinates and momenta of the physical system and
the corresponding group action in the associated Hilbert
space of states; the determination of those subspaces
that are mapped irreducibly onto themselves by the
group action; the Lie algebra and its actions as derived
from the group actions, and conversely; the construction
of composite objects from elementary constituents, us-
ing the notion of tensor product space and Kronecker
products of representations, which are the basic pre-
cepts in quantum theory for building complex systems
from simpler ones; the reduction of the Kronecker prod-
uct of irreducible representations into irreducibles with
the associated Wigner–Clebsch–Gordan and Racah co-
efficients determining not only this reduction, but also
having a dual role in the construction of the irreducible
state spaces themselves; and, finally, the repetition of
this process for many-particle systems with the atten-
dant theory of 3n − j coefficients. The universality of
this methodology may be attributed to being able, in
favorable situations, to separate the particular conse-
quences of physical law (e.g., the Coulomb force) from
the implications of symmetry imposed on the system by
our underlying conceptions of space and time. Empiric-
al models based on symmetry that attempt to identify
the more important ingredients underlying observed
physical phenomena are also of great importance.
The group actions in complex systems are often
modeled after the following examples for the actions
of the groups SO(3, R) and SU(2) on functions defined
over the 2-sphere S
2
⊂ R
3
:
Hilbert space:
V ={f | f is a polynomial satisfying ∇
2
f(x) = 0} .
Inner or scalar product:
f, f
=
unit sphere
f
∗
(x) f
(x)dS ,
where f(x) = f(X) for x presented in the Cartan matrix
form X.
Group actions:
(O
R
f )(x) = f
R
−1
x
, each f ∈ V ,
each x ∈ R
3
,
(T
U
f )(X) = f
U
†
XU
, each f ∈ V ,
each X ∈ H
2
.
Operator properties:
•
O
R
is a unitary operator on V;thatis,
(O
R
f, O
R
f
) = ( f, f
).
•
T
U
is a unitary operator on V;thatis,(T
U
f, T
U
f
) =
( f, f
).
•
R → O
R
is a unitary representation of SO(3, R);
that is, O
R
1
O
R
2
= O
R
1
R
2
.
•
U → T
U
is a unitary representation of SU(2);that
is, T
U
1
T
U
2
= T
U
1
U
2
.
•
O
R(U)
= T
U
= T
−U
is an operator identity on the
space V.
One parameter subgroups:
U
j
(t) = exp(−itσ
j
/2), t ∈ R, j = 1, 2, 3 ;
R
j
(t) = R(U
j
(t)) = exp(−itM
j
),
t ∈ R, j = 1, 2, 3 ;
where
M
1
= i
00 0
00−1
01 0
, M
2
= i
001
000
−100
,
M
3
= i
0 −10
100
000
.
(2.4)
Part A 2
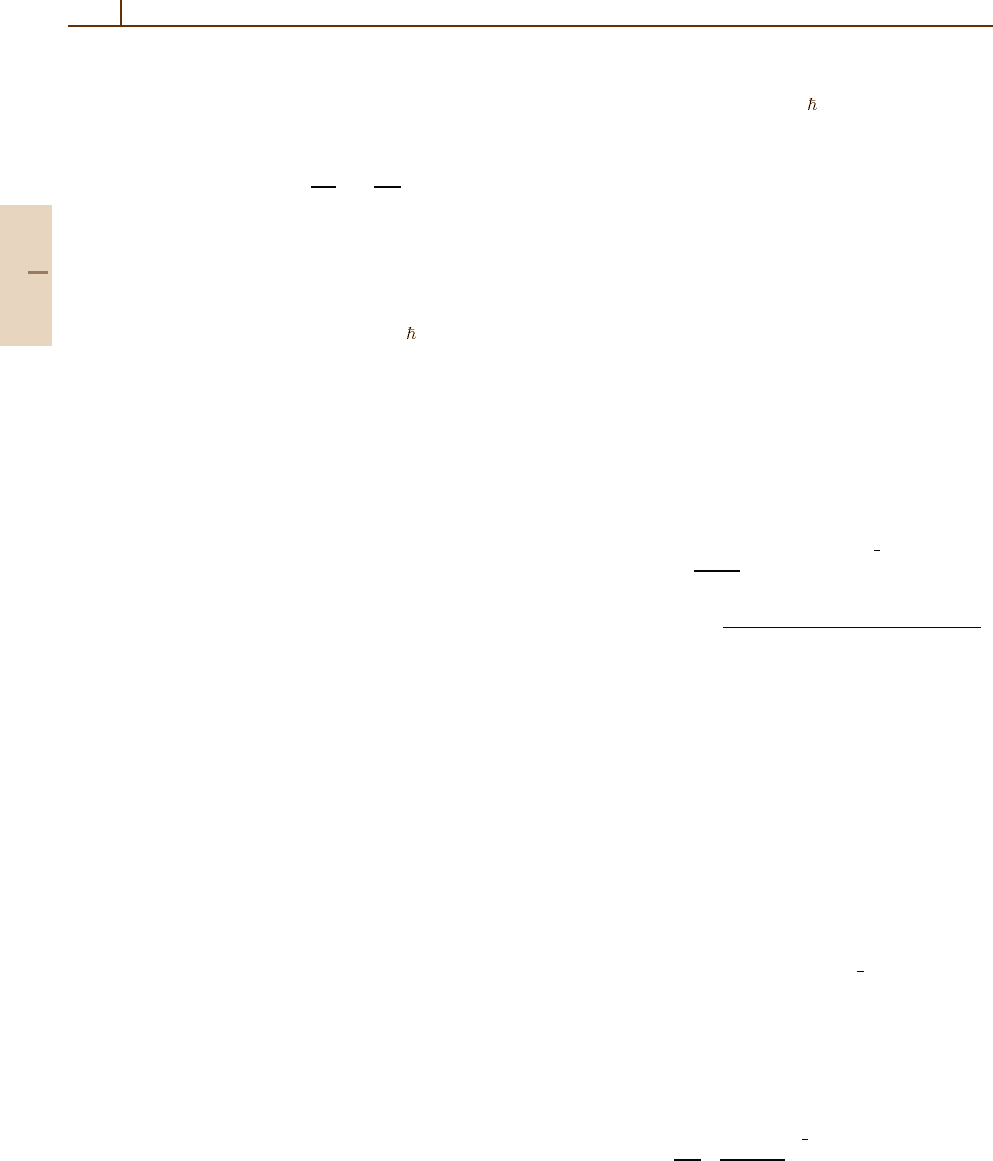
12 Part A Mathematical Methods
Infinitesimal generators:
L
j
= i(dO
R
j
(t)
/dt)
t=0
,
L
j
= i(dT
U
j
(t)
/dt)
t=0
,
(L
j
f )(x) =−i
x
k
∂
∂x
l
−x
l
∂
∂x
k
f(x),
j, k, l cyclic in 1, 2, 3 .
(2.5)
Historically, the algebra of angular momentum came
about through the quantum rule of replacing the lin-
ear momentum p of a classical point particle, which
is located at position r,by p →−i
∇, thus replacing
the classical angular momentum r × p about the origin
of a chosen Cartesian inertial system by the angular
momentum operator:
L =−i r × ∇ (in units of
). (2.6)
The quantal angular momentum properties of this sim-
ple one-particle system are then to be inferred from the
properties of these operators and their actions in the
associated Hilbert space. This remains the method of in-
troducing angular momentum theory in most textbooks
because of its simplicity and historical roots. It also
leads to focusing the developments of the theory on
the algebra of operators in contrast to emphasizing the
associated group transformations of the Hilbert space,
although the two viewpoints are intimately linked, as
illustrated above. Both perspectives will be presented
here.
2.1 Orbital Angular Momentum
The model provided by orbital angular momentum oper-
ators is the paradigm for standardizing many of the
conventions and relations used in more abstract and
general treatments. These basic results for the orbital
angular momentum operator L =−i r × ∇ acting in the
vector space V are given in this section both in Carte-
sian coordinates x = col (x
1
, x
2
, x
3
) and spherical polar
coordinates:
x = (r sin θ cos φ, r sin θ sin φ, r cos θ) ,
0 ≤r < ∞ , 0 ≤φ<2π, 0 ≤ θ ≤ π.
2.1.1 Cartesian Representation
Commutation relations:
Cartesian form:
[L
1
, L
2
]=iL
3
, [L
2
, L
3
]=iL
1
,
[L
3
, L
1
]=iL
2
.
Cartan form:
[L
3
, L
+
]=L
+
, [L
3
, L
−
]=−L
−
,
[L
+
, L
−
]=2L
3
.
Squared orbital angular momentum:
L
2
= L
2
1
+L
2
2
+L
2
3
= L
−
L
+
+L
3
(L
3
+1)
= L
+
L
−
+L
3
(L
3
−1)
=−r
2
∇
2
+(x·∇)
2
+(x·∇).
L
2
, L
3
form a complete set of commuting Hermitian
operators in V with eigenfunctions
Y
lm
(x) =
2l+1
4π
(l+m)!(l−m)!
1
2
×
k
(−x
1
−ix
2
)
k+m
(x
1
−ix
2
)
k
x
l−m−2k
3
2
2k+m
(k+m)!k !(l−m −2k)!
,
where l = 0, 1, 2,... ,; m = l, l−1, ... ,−l.
Homogeneous polynomial solutions of Laplace’s equa-
tion:
Y
lm
(λx) = λ
l
Y
lm
(x),
(x·∇)Y
lm
(x) =lY
lm
(x),
∇
2
Y
lm
(x) = 0 .
Complex conjugate:
Y
∗
lm
(x) = (−1)
m
Y
l,−m
(x).
Action of angular momentum operators:
L
±
Y
lm
(x) =[(l∓m)(l±m +1)]
1
2
Y
l,m±1
(x),
L
3
Y
lm
(x) = mY
lm
(x),
L
2
Y
lm
(x) =l(l+1)Y
lm
.
Highest weight eigenfunction:
L
+
Y
ll
(x) = 0 , L
3
Y
ll
(x) =lY
ll
(x),
Y
ll
(x) =
1
2
l
l!
(2l+1)!
4π
1
2
(−x
1
−ix
2
)
l
.
Part A 2.1
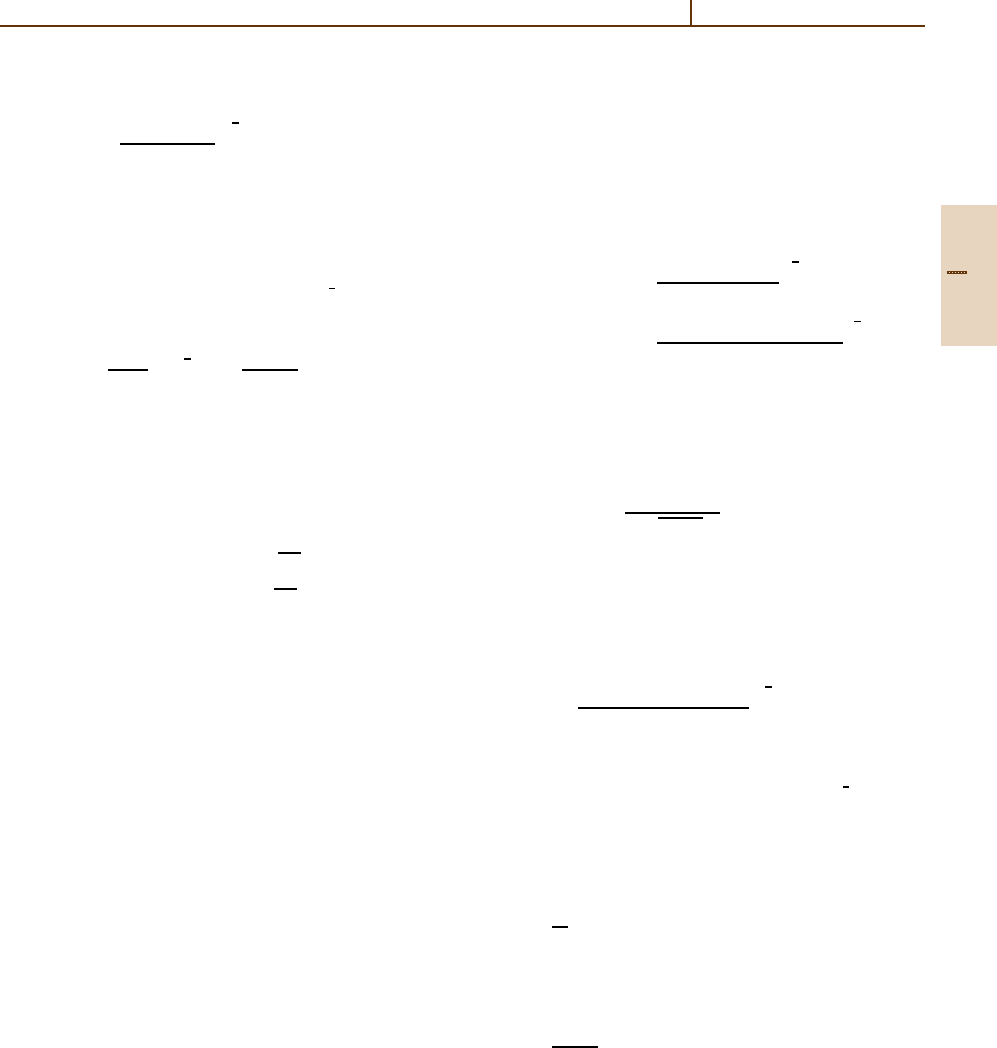
Angular Momentum Theory 2.1 Orbital Angular Momentum 13
Generation from highest weight:
Y
lm
(x) =
(l+m)
(2l)!(l−m)!
1
2
L
l−m
−
Y
ll
(x).
Relation to Gegenbauer and Jacobi polynomials:
Y
lm
(x) =r
l−
|
m
|
Y
m
(x
1
, x
2
)
× [(2l+1)(l+m)!(l−m)!/2]
1
2
× H
l,
|
m
|
(x
3
/r),
H
lλ
(z) =
(2λ)!
2
λ
λ!
C
λ+
1
2
l−λ
(z) =
(l+λ)!
2
λ
l!
P
(λ,λ)
l−λ
(z),
0 ≤ λ ≤l = 0, 1, 2,... ,
where the Y
m
(x
1
, x
2
) are homogeneous polynomial
solutions of degree |m| of Laplace’s equation in
2-space, R
2
:
Y
m
(x
1
, x
2
) =
(−x
1
−ix
2
)
m
/
√
2π, m ≥0 ,
(x
1
−ix
2
)
−m
/
√
2π, m ≤0 .
(Section 2.1.2 for the definition of Gegenbauer and
Jacobi polynomials.)
Orthogonal group action:
(O
R
Y
lm
)(x) = Y
lm
(R
−1
x) =
m
D
l
m
m
(R)Y
lm
(x),
where the functions D
l
m
m
(R) = D
l
m
m
(U(R)) are
defined in Sect. 2.3 for various parametrizations
of R.
Unitary group action:
(T
U
Y
lm
)(X) = Y
lm
(U
†
XU )
=
m
D
l
m
m
(U)Y
lm
(X),
where the functions D
l
m
m
(U) are defined in Sects. 2.2
and 2.3.
Orthogonality on the unit sphere:
unit sphere
Y
∗
l
m
(x)Y
lm
(x)dS =δ
l
l
δ
m
m
.
Product of solid harmonics:
Y
kµ
(x)Y
lm
(x) =
l
l
||Y
k
||lC
lkl
m,µ,m+µ
Y
l
,m+µ
(x)
=
l
(l
||Y
k
||l)
lk l
m µ −m −µ
× (−1)
l
+m+µ
Y
l
,m+µ
(x),
l
||Y
k
||l=r
l+k−l
(2l+1)(2k+1)
4π(2l
+1)
1
2
C
lkl
000
,
(l
||Y
k
||l) =r
l+k−l
(2l+1)(2k+1)(2l
+1)
4π
1
2
× (−1)
l
lkl
000
,
where C
l
1
l
2
l
m
1
m
2
m
and
l
1
l
2
l
m
1
m
2
−m
=
(−1)
l
1
−l
2
+m
√
2l+1
C
l
1
l
2
l
m
1
m
2
m
denote Wigner–Clebsch–Gordan coefficients and 3– j
coefficients, respectively (Sect. 2.7).
Vector addition theorem for solid harmonics:
Y
lm
(z +z
) =
kµ
4π(2l+1)!
(2l−2k+1)!(2k+1)!
1
2
C
l−k,k ,l
m−µ,µ,m
× Y
l−k,m−µ
(z)Y
kµ
(z
), z, z
∈ C
3
,
C
j−k,k,l
m−µ,µ,m
=
l+m
k+µ
l−m
k−µ
2l
2k
1
2
.
Rotational invariant in two vectors:
I
l
(x, y) =
1
2
l
k
(−1)
k
l
k
2l−2k
l
× (x· y)
l−2k
(x·x)
k
( y· y)
k
= (x·x)
l/2
( y· y)
l/2
C
(1/2)
l
(
ˆ
x·
ˆ
y)
=
4π
2l+1
m
(−1)
m
Y
lm
(x)Y
l,−m
( y),
where C
(1/2)
l
(z) is a Gegenbauer polynomial
(Sect. 2.1.2)and
ˆ
x = x/|x| ,
ˆ
y = y/|y| , cos θ =
ˆ
x·
ˆ
y .
Part A 2.1
14 Part A Mathematical Methods
Legendre polynomials:
P
l
(cos θ) =
4π
2l+1
m
(−1)
m
Y
l,−m
(
ˆ
y)Y
lm
(
ˆ
x),
4π
2l+1
1
2
Y
l0
(x)
=
1
2
l
k
(−1)
k
l
k
2l−2k
l
x
l−2k
3
(x·x)
k
=r
l
P
l
(x
3
/r).
Rayleigh plane wave expansion:
e
ik·x
= 4π
∞
l=0
l
m=−l
i
l
j
l
(kr)Y
∗
lm
ˆ
k
Y
lm
(
ˆ
x),
j
l
(kr) =
π
2kr
1
2
J
l+1/2
(kr).
Relations in potential theory:
Y
lm
(∇)
1
r
=
(−1)
l
(2l)!
2
l
l!
Y
lm
(x)
r
2l+1
,
1/R =
∞
l=0
I
l
(x, y)/r
2l+1
,
I
l
(x, y)/r
2l+1
=
(−1)
l
l!
(y·∇)
l
1
r
.
For R= x− y , r = (x·x)
1
2
, s = ( y· y)
1
2
,
1/R =
l
P
l
(cos θ)
s
l
r
l+1
, s ≤r, cos θ =
ˆ
x·
ˆ
y .
Rotational invariants in three vectors:
I
(l
1
l
2
l
3
)
x
1
, x
2
, x
3
=
(4π)
3/2
[
(2l
1
+1)(2l
2
+1)(2l
3
+1)
]
1
2
×
m
1
m
2
m
3
l
1
l
2
l
3
m
1
m
2
m
3
× Y
l
1
m
1
x
1
Y
l
2
m
2
x
2
Y
l
3
m
3
x
3
,
where
l
1
l
2
l
3
m
1
m
2
m
3
is a 3–j coefficient (Sect. 2.7).
I
(l
1
l
2
l
3
)
x
1
, x
2
, 0
= δ
l
1
l
2
δ
l
3
0
(−1)
l
1
I
l
1
x
1
, x
2
2l
1
+1
1
2
.
Product law:
I
(l)
(x)I
(k)
(x)
=
( j)
3
α=1
(−1)
j
α
(2 j
α
+1)
l
α
k
α
j
α
000
× (x
α
·x
α
)
(l
α
+k
α
−j
α
)/2
l
1
l
2
l
3
k
1
k
2
k
3
j
1
j
2
j
3
I
( j)
(x),
where l = (l
1
, l
2
, l
3
), etc., x =
x
1
, x
2
, x
3
.
Coplanar vectors:
I
(l)
x
1
, x
2
,αx
1
+βx
2
=
kl
(2l
3
+1)!
(2l
3
−2k)!(2k)!
1
2
× α
l
3
−k
β
k
(−1)
l
1
+l
3
+k
(2l+1)
×
l
3
−kl
1
l
000
kl
2
l
000
l
3
−kl
3
k
l
2
ll
1
×
x
1
·x
1
(l
1
+l
3
−l−k)/2
x
2
·x
2
(l
2
+k−l)/2
× I
l
x
1
, x
2
.
The bracket symbols in these relations are 6–j and 9–j
coefficients (Sects. 2.9, 2.10).
Cartan’s vectors of zero length:
α =
−z
2
1
+z
2
2
, −i
z
2
1
+z
2
2
, 2z
1
z
2
,
α ·α = α
2
1
+α
2
2
+α
2
3
= 0 ,
z =(z
1
, z
2
) ∈ C
2
.
Solutions of Laplace’s equation using vectors of zero
length:
∇
2
(α ·x)
l
= 0 , l =0, 1,... .
Solid harmonics for vectors of zero length:
(−1)
m
Y
l,−m
(α) =
(2l)!
l!
2l+1
4π
1
2
P
lm
(z
1
, z
2
),
P
lm
(z
1
, z
2
) =
z
l+m
1
z
l−m
2
√
(l+m)!(l−m)!
.
Orbital angular momentum operators for vectors of zero
length:
J =−i(α × ∇
α
),
J
+
= z
1
∂
∂z
2
, J
−
= z
2
∂
∂z
1
,
J
3
=
1
2
z
1
∂
∂z
1
−z
2
∂
∂z
2
.
Part A 2.1
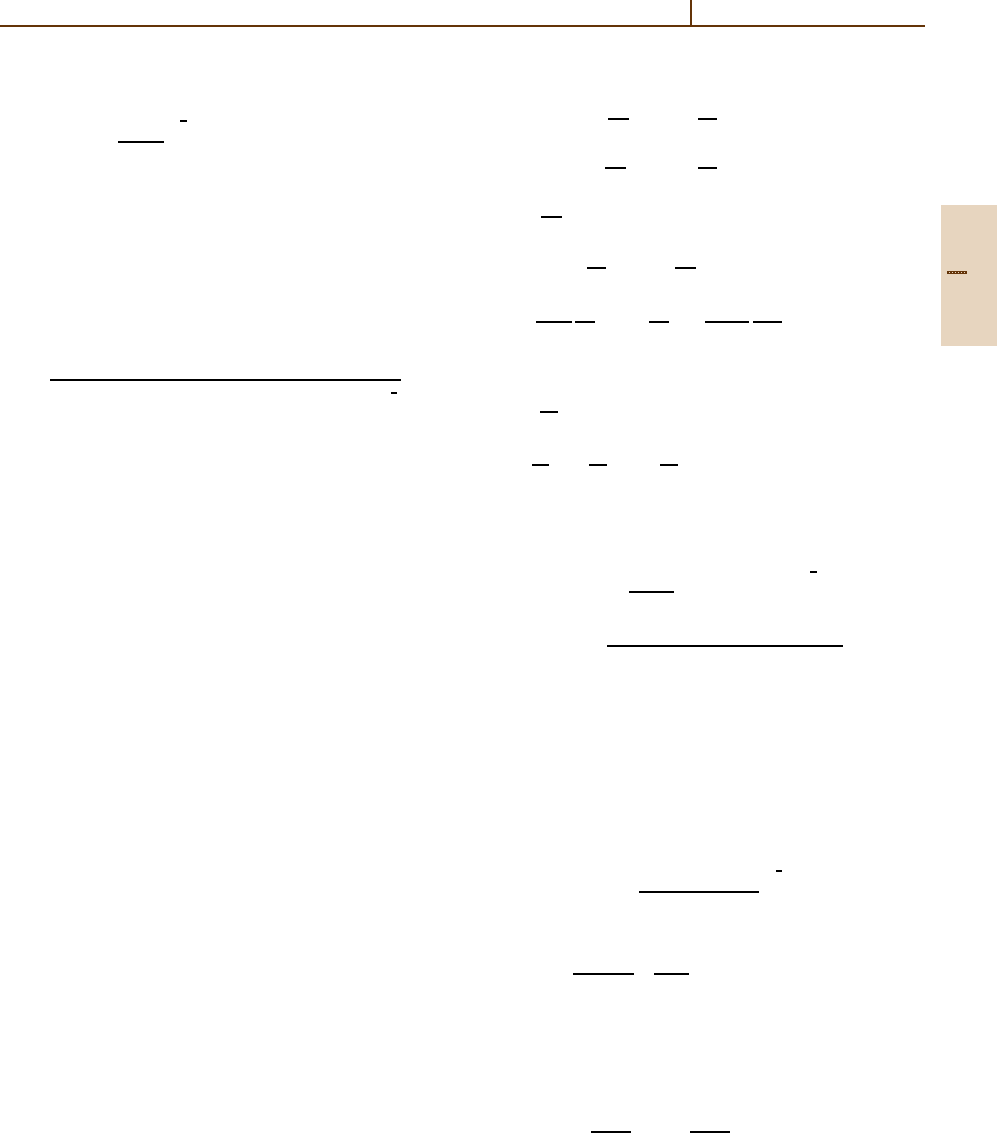
Angular Momentum Theory 2.1 Orbital Angular Momentum 15
Rotational invariant for vectors of zero length:
(α ·x)
l
=
4π
2l+1
1
2
2
l
l!
m
P
lm
(z)Y
lm
(x).
Spinorial invariant under z
i
→Uz
i
(i = 1, 2, 3):
m
1
m
2
m
3
j
1
j
2
j
3
m
1
m
2
m
3
P
j
1
m
1
z
1
P
j
2
m
2
z
2
P
j
3
m
3
z
3
=[( j
1
+ j
2
+ j
3
+1)!]
−1/2
×
z
12
12
j
1
+j
2
−j
3
z
31
12
j
3
+j
1
−j
2
z
23
12
j
2
+j
3
−j
1
[( j
1
+ j
2
− j
3
)!( j
3
+ j
1
− j
2
)!( j
2
+ j
3
− j
1
)!]
1
2
,
z
ij
12
= z
i
1
z
j
2
−z
j
1
z
i
2
.
This relation is invariant under the transformation
z →Uz =
(Uz)
1
,(Uz)
2
= (u
11
z
1
+u
12
z
2
, u
21
z
1
+u
22
z
2
),
where U ∈ SU(2). Transformation properties of vectors
of zero length:
α → Rα, α = col(α
1
,α
2
,α
3
),
where z →Uz and R is given in terms of U in the be-
ginning of this chapter. Simultaneous eigenvectors of L
2
and J
2
:
L
2
(α ·x)
l
=l(l+1)(α ·x)
l
, l =0, 1,... ,
J
2
(α ·x)
l
=l(l+1)(α ·x)
l
, l =0, 1,... .
2.1.2 Spherical Polar Coordinate
Representation
The results given in Sect. 2.1.1 may be presented in any
system of coordinates well-defined in terms of Cartesian
coordinates. The principal relations for spherical polar
coordinates are given in this section, where a vector
in R
3
is now given in the form
x =r
ˆ
x =r(sin θ cos φ, sin θ sin φ, cos θ) ,
0 ≤ θ ≤ π, 0 ≤φ<2π.
Orbital angular momentum operators:
L
1
= icosφ cot θ
∂
∂φ
+isinφ
∂
∂θ
,
L
2
= isinφ cot θ
∂
∂φ
−icosφ
∂
∂θ
,
L
3
=−i
∂
∂φ
,
L
±
= e
±iφ
±
∂
∂θ
+icotθ
∂
∂φ
,
L
2
=−
1
sin θ
∂
∂θ
sin θ
∂
∂θ
−
1
sin
2
θ
∂
2
∂φ
2
.
Laplacian:
x·∇=r
∂
∂r
,
∇
2
=
1
r
2
r
∂
∂r
2
+r
∂
∂r
−L
2
.
Spherical harmonics
solid harmonics on the unit
sphere S
2
:
Y
lm
(θ, φ) = (−1)
m
2l+1
4π
(l+m)!(l−m)!
1
2
e
imφ
×
k
(−1)
k
(sin θ)
2k+m
(cos θ)
l−2k−m
2
2k+m
(k+m)!k !(l−2k−m)!
.
Orthogonality on the unit sphere:
2π
0
dφ
π
0
dθ sin θ Y
∗
l
m
(θ, φ) Y
lm
(θ, φ) = δ
l
l
δ
m
m
.
Relation to Legendre, Jacobi, and Gegenbauer poly-
nomials:
Y
lm
(θ, φ) = (−1)
m
(2l+1)(l−m)!
4π(l+m)!
1
2
× P
m
l
(cos θ) e
imφ
,
P
m
l
(cos θ) =
(l+m)!
l!
sin θ
2
m
P
(m,m)
l−m
(cos θ) .
Jacobi polynomials:
P
(α,β)
n
(x ) =
s
n +α
s
n +β
n −s
×
x −1
2
n−s
x +1
2
s
,
n = 0, 1,... ,
Part A 2.1
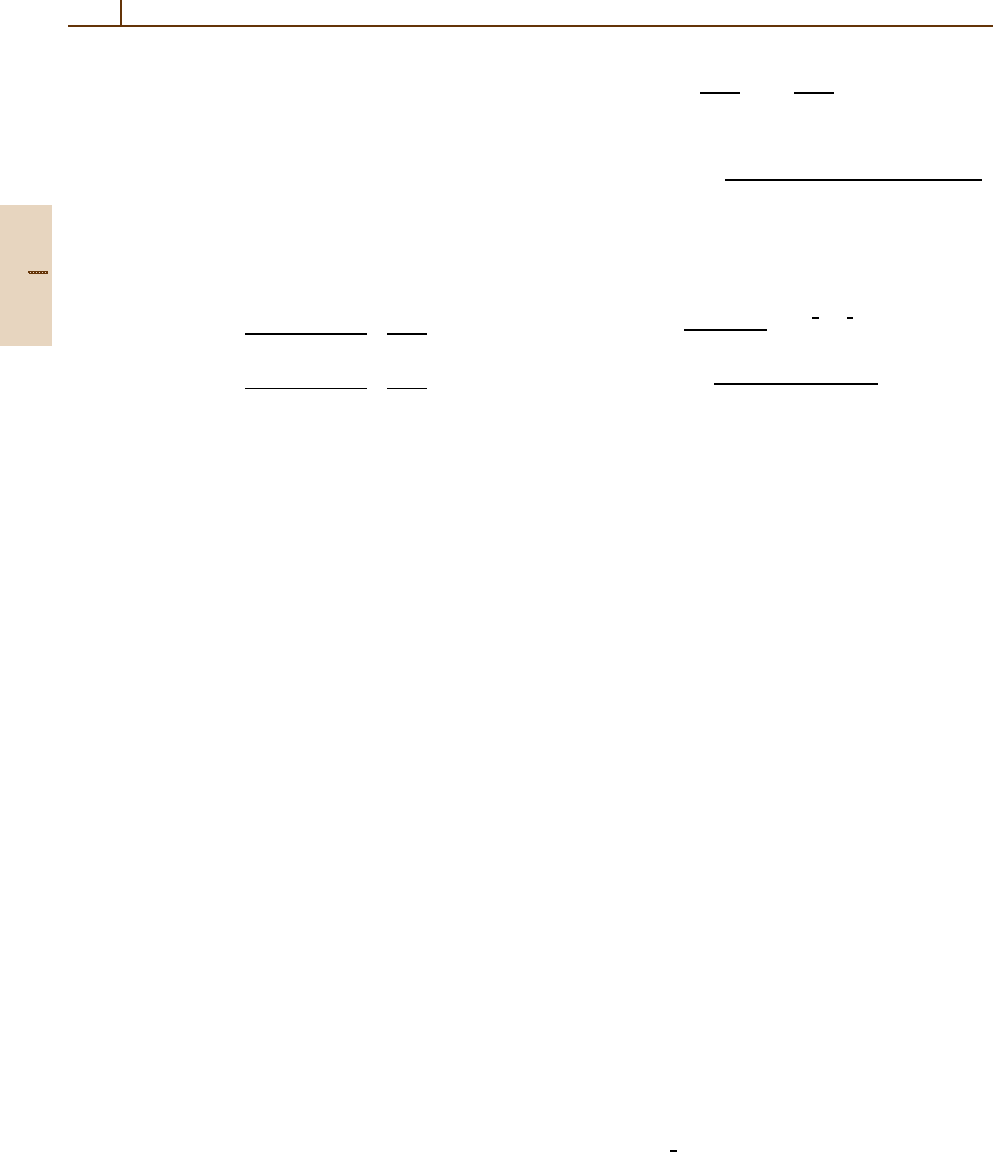
16 Part A Mathematical Methods
where α, β are arbitrary parameters and
z
k
=
z(z−1) ···(z −k+1)/k!
for k =1, 2,...
1fork =0
0fork =−1, −2,...
Relations between Jacobi polynomials for n +α,
n +β, n +α +β nonnegative integers:
P
α,β
n
(x) =
(n+α)!(n+β)!
n!(n +α +β)!
x +1
2
−β
P
(α,−β)
n+β
(x ),
P
α,β
n
(x) =
(n+α)!(n+β)!
n!(n +α +β)!
x −1
2
−α
P
(−α,β)
n+α
(x),
P
α,β
n
(x) =
x −1
2
−α
x +1
2
−β
P
(−α,−β)
n+α+β
(x).
Nonstandard form (α arbitrary):
P
(α,α)
n
(x) =
s
(−1)
s
(α +s+1)
n−s
1−x
2
s
x
n−2s
2
2s
s!(n−2s)!
,
(z)
k
= z(z +1) ···(z+k−1), k = 1, 2,... ;
(z)
0
= 1 .
Gegenbauer polynomials (α > −1/2):
C
(α)
n
(x) =
(2α)
n
(α +1/2)
n
P
α−
1
2
,α−
1
2
n
(x)
=
s
(−1)
s
(α)
n−s
(2x)
n−2s
s!(n−2s)!
.
2.2 Abstract Angular Momentum
Abstract angular momentum theory addresses the prob-
lem of constructing all finite Hermitian matrices, up
to equivalence, that satisfy the same commutation
relations
[J
1
, J
2
]=iJ
3
, [J
2
, J
3
]=iJ
1
, [J
3
, J
1
]=iJ
2
(2.7)
as some set of Hermitian operators J
1
, J
2
, J
3
appro-
priately defined in some Hilbert space; that is, of
constructing all finite Hermitian matrices M
i
such that
under the correspondence J
i
→ M
i
(i =1, 2, 3) the com-
mutation relations are still obeyed. If M
1
, M
2
, M
3
is such a set of Hermitian matrices, then AM
1
A
−1
,
AM
2
A
−1
, AM
3
A
−1
, is another such set, where A is
an arbitrary unitary matrix. This defines what is meant
by equivalence. The commutation relations (2.7)may
also be formulated as:
[J
3
, J
±
]=±J
±
, [J
+
, J
−
]=2J
3
,
J
±
= J
1
±iJ
2
, J
†
+
= J
−
. (2.8)
The squared angular momentum
J
2
= J
2
1
+ J
2
2
+ J
2
3
= J
−
J
+
+ J
3
(J
3
+1)
= J
+
J
−
+ J
3
(J
3
−1) (2.9)
commutes with each J
i
, and J
3
is, by convention, taken
with J
2
as a pair of commuting Hermitian operators to
be diagonalized.
Examples of matrices satisfying relations (2.7)are
provided by J
i
→ σ
i
/2 [the 2 × 2 Hermitian Pauli ma-
trices defined in (2.1)] and J
i
→ M
i
[the 3 × 3 matrices
defined in (2.4)], these latter matrices being equivalent
to those obtained from the matrices of the orbital angular
momentum operators for l = 1.
One could determine all Hermitian matrices solv-
ing (2.7)and(2.8) by using only matrix theory, but it
is customary in quantum mechanics to formulate the
problem using Hilbert space concepts appropriate to
that theory. Thus, one takes the viewpoint that the J
i
are linear Hermitian operators with an action defined in
a separable Hilbert space H such that J
i
: H → H .
One then seeks to decompose the Hilbert space into
a direct sum of subspaces that are irreducible with re-
spect to this action; that is, subspaces that cannot be
further decomposed as a direct sum of subspaces that
all the J
i
leave invariant (map vectors in the space into
vectors in the space). In this section, the solution of this
fundamental problem for angular momentum theory is
given. These results set the notation and phase conven-
tions for all of angular momentum theory, in all of its
varied realizations, and the relations are therefore some-
times referred to as standard. The method most often
used to solve the posed problem is called the method of
highest weights.
The solution of this problem is among the most im-
portant in quantum theory because of its generality and
applicability to a wide range of problems. The space H
can be written as a direct sum
H =
j=0,
1
2
,1,...
⊕n
j
H
j
,
each H
j
⊥ H
j
, j = j
, (2.10)
Part A 2.2

Angular Momentum Theory 2.2 Abstract Angular Momentum 17
in which H
j
denotes a vector space of dimension 2 j +1
that is invariant and irreducible under the action of the
set of operators J
i
, i = 1, 2, 3, and where the direct sum
is over all half integers j = 0,
1
2
, 1,....Theremaybe
multiple occurrences, n
j
in number, of the same space
H
j
for given j, or no such space, n
j
= 0, in the di-
rect sum. Abstractly, in so far as angular momentum
properties are concerned, each repeated space H
j
is
identical. Such spaces may, however, be distinguished
by their properties with respect to other physical ob-
servables, but not by the angular action of momentum
operators themselves. The result, (2.10), applies to any
physical system, no matter how complex, in which ro-
tational symmetry, hence SU(2) symmetry, is present,
even in situations of higher symmetry where SU(2) is
a subgroup. Indeed, the resolution of the terms in (2.10)
for various physical systems constitutes “spectroscopy”
in the broadest sense.
The characterization of the space H
j
with respect to
angular momentum properties is given by the following
results, where basis vectors are denoted in the Dirac
braket notation.
Orthonormal basis:
{
|
jm
|
m =−j, −j +1,... , j} .
(2.11)
jm
| jm=δ
m
,m
. (2.12)
Simultaneous eigenvectors:
J
2
| jm=j( j +1)| jm , J
3
| jm=m| jm.
(2.13)
Action of angular momentum operators:
J
+
| jm=[( j −m)( j +m +1)]
1/2
| jm +1 ,
J
−
| jm=[( j +m)( j −m +1)]
1/2
| jm −1 .
(2.14)
Defining properties of highest weight vector:
J
+
| jj=0 , J
3
| jj=j| jj .
Generation of general vector from highest weight:
| jm=
( j +m)!
(2 j)!( j −m)!
1/2
J
j−m
−
| jj .
Necessary property of lowest weight vector:
J
−
| j, −j=0 , J
3
| j, −j=−j | j, −j .
Operator in H corresponding to a rotation by angle ψ
about direction
ˆ
n in R
3
:
T
U(ψ,
ˆ
n)
= exp(−iψ
ˆ
n· J),
ˆ
n·
ˆ
n =n
2
1
+n
2
2
+n
2
3
= 1 ,
ˆ
n· J = n
1
J
1
+n
2
J
2
+n
3
J
3
,
U(ψ,
ˆ
n) =exp(−iψ
ˆ
n·σ/2)
= σ
0
cos
1
2
ψ
−i(
ˆ
n·σ) sin
1
2
ψ
=
cos
1
2
ψ
−in
3
sin
1
2
ψ
(−in
1
−n
2
) sin
1
2
ψ
(−in
1
+n
2
) sin
1
2
ψ
cos
1
2
ψ
+in
3
sin
1
2
ψ
,
0 ≤ ψ ≤ 2π,
(2.15)
where σ
0
denotes the 2 ×2 unit matrix.
Action of T
U(ψ,
ˆ
n)
on H
j
:
T
U
| jm=
m
D
j
m
m
(U)| jm
, (2.16)
in which U = U(ψ,
ˆ
n) and D
j
m
m
(U) denotes a homoge-
neous polynomial of degree 2 j defined on the elements
u
ij
= U
ij
(ψ,
ˆ
n) in row i and column j of the matrix
U(ψ,
ˆ
n) givenby(2.15). The explicit form of this poly-
nomial is
D
j
m
m
(U)
=[( j +m)!( j −m)!( j +m
)!( j −m
)!]
1
2
×
α
(u
11
)
α
11
(u
12
)
α
12
(u
21
)
α
21
(u
22
)
α
22
α
11
!α
12
!α
21
!α
22
!
.
(2.17)
The notation α symbolizes a 2 × 2 array of nonnegative
integers with certain constraints:
α
11
α
12
α
21
α
22
j +m
j −m
j +mj−m
.
In this array the α
ij
are nonnegative integers subject to
the row and column constraints (sums) indicated by the
(nonnegative) integers j ±m, j ±m
. Explicitly,
α
11
+α
12
= j +m
,α
21
+α
22
= j −m
,
α
11
+α
21
= j +m ,α
12
+α
22
= j −m .
The summation is over all such arrays. Any one of the α
ij
may serve as a single summation index if one wishes to
Part A 2.2
