Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics
Подождите немного. Документ загружается.


18 Part A Mathematical Methods
eliminate the redundancy inherent in the square-array
notation. The form (2.17) is very useful for obtaining
symmetry relations for these polynomials (Sect. 2.3.6).
Unitary property on H:
T
U
Ψ |T
U
Ψ =Ψ |Ψ , each Ψ ∈ H .
Irreducible unitary matrix representation of SU(2):
(D
j
(U))
j−m
+1, j−m+1
= D
j
m
m
(U),
m
= j, j −1,... ,−j ; m = j, j −1,... ,−j ,
(2.18)
denotes the element in row j −m
+1andcolumn
j −m +1. Then, dimension of D
j
(U) = 2 j +1and
D
j
(U)D
j
(U
) = D
j
(UU
),
U ∈ SU(2), U
∈ SU(2),
(D
j
(U))
†
= (D
j
(U))
−1
= D
j
(U
†
).
Kronecker (direct) product representation:
D
j
1
(U) × D
j
2
(U)
is a (2 j
1
+1)(2 j
2
+1) dimensional reducible represen-
tation of SU(2). One can also effect the reduction of this
representation into irreducible ones by abstract methods.
The results are given in Sect. 2.7.
2.3 Representation Functions
2.3.1 Parametrizations
of the Groups SU(2) and SO(3,R)
The irreducible representations of the quantal rotation
group, SU(2), are among the most important quan-
tities in all of angular momentum theory: These are
the unitary matrices of dimension 2 j +1, denoted by
D
j
(U), where this notation is used to signify that the
elements of this matrix, denoted D
j
m
m
(U), are func-
tions of the elements u
ij
of the 2 × 2 unitary unimodular
matrix U ∈ SU(2). It has become standard to enumer-
ate the rows and columns of these matrices in the order
j, j −1,... ,−j as read from top to bottom down the
rows and from left to right across the columns [see
also (2.18)]. These matrices may be presented in a va-
riety of parametrizations, all of which are useful. In
order to make comparisons between the group SO(3, R)
and the group SU(2), it is most useful to parametrize
these groups so that they are related according to the
two-to-one homomorphism given by (2.2).
The general parametrization of the group SU(2) is
given in terms of the Euler–Rodrigues parameters cor-
responding to points belonging to the surface of the unit
sphere S
3
in R
4
,
α
2
0
+α
2
1
+α
2
2
+α
2
3
= 1 . (2.19)
Each U ∈ SU(2) can be written in the form:
U(α
0
, α) =
α
0
−iα
3
−iα
1
−α
2
−iα
1
+α
2
α
0
+iα
3
= α
0
σ
0
−iα ·σ . (2.20)
The R ∈ SO(3, R) corresponding to this U in the two-
to-one homomorphism given by (2.2)is:
R(α
0
, α) =
α
2
0
+α
2
1
−α
2
2
−α
2
3
2α
1
α
2
−2α
0
α
3
2α
1
α
3
+2α
0
α
2
2α
1
α
2
+2α
0
α
3
α
2
0
+α
2
2
−α
2
3
−α
2
1
2α
2
α
3
−2α
0
α
1
2α
1
α
3
−2α
0
α
2
2α
2
α
3
+2α
0
α
1
α
2
0
+α
2
3
−α
2
1
−α
2
2
.
(2.21)
The procedure of parametrization is implemented
uniformly by first parametrizing the points on the unit
sphere S
3
so as to cover the points in S
3
exactly once,
thus obtaining a parametrization of each U ∈ SU(2).
Equation (2.21) is then used to obtain the correspond-
ing parametrization of each R ∈ SO(3, R), where one
notes that R(−α
0
, −α) = R(α
0
, α). Because of this two-
to-one correspondence ±U→R, the domain of the
parameters that cover the unit sphere S
3
exactly once
will cover the group SO(3, R) exactly twice. This is
taken into account uniformly by redefining the domain
for SO(3, R) so as to cover only the upper hemisphere
(α
0
≥ 0) of S
3
.
In the active viewpoint (reference frame fixed with
points being transformed into new points), an ar-
bitrary vector x = col(x
1
, x
2
, x
3
) ∈ R
3
is transformed
to the new vector x
= col
x
1
, x
2
, x
3
by the rule
x
= Rx, or, equivalently, in terms of the Cartan ma-
trix: X
=UXU
†
. In the passive viewpoint, the basic
inertial reference system, which is taken to be a right-
handed triad of unit vectors (
ˆ
e
1
,
ˆ
e
2
,
ˆ
e
3
), is transformed
by R to a new right-handed triad
ˆ
f
1
,
ˆ
f
2
,
ˆ
f
3
by the
Part A 2.3

Angular Momentum Theory 2.3 Representation Functions 19
rule
ˆ
f
j
=
i
R
ij
ˆ
e
i
, i = 1, 2, 3 ,
so that
ˆ
e
i
·
ˆ
f
j
= R
ij
. In this viewpoint, the coordinates
of one and the same point P undergo a redescription
under the change of frame. If the coordinates of P
are (x
1
, x
2
, x
3
) relative to the frame (
ˆ
e
1
,
ˆ
e
2
,
ˆ
e
3
) and
x
1
, x
2
, x
3
relative to the frame
ˆ
f
1
,
ˆ
f
2
,
ˆ
f
3
,then
x
1
ˆ
e
1
+x
2
ˆ
e
2
+x
3
ˆ
e
3
= x
1
ˆ
f
1
+x
2
ˆ
f
2
+x
3
ˆ
f
3
,
so that x
= R
T
x.
Rotation about direction
ˆ
n ∈ S
2
by positive angle ψ
(right-hand rule):
(α
0
, α) =
cos
1
2
ψ,
ˆ
nsin
1
2
ψ
, 0 ≤ψ ≤ 2π,
U(ψ,
ˆ
n) =exp
−i
1
2
ψ
ˆ
n·σ
=
cos
1
2
ψ −in
3
sin
1
2
ψ(−in
1
−n
2
) sin
1
2
ψ
(−in
1
+n
2
) sin
1
2
ψ cos
1
2
ψ +in
3
sin
1
2
ψ
,
R(ψ,
ˆ
n) =exp(−iψ
ˆ
n· M), 0 ≤ψ ≤ π
= I
3
−isinψ(
ˆ
n· M) −(
ˆ
n· M)
2
(1 −cos ψ)
=
R
11
R
12
R
13
R
21
R
22
R
23
R
31
R
32
R
33
,
R
11
= n
2
1
+
1 −n
2
1
cos ψ,
R
21
= n
1
n
2
(1 −cos ψ) +n
3
sin ψ,
R
31
= n
1
n
3
(1 −cos ψ) −n
2
sin ψ,
R
12
= n
1
n
2
(1 −cos ψ) −n
3
sin ψ,
R
22
= n
2
2
+
1 −n
2
2
cos ψ,
R
32
= n
2
n
3
(1 −cos ψ) +n
1
sin ψ,
R
13
= n
1
n
3
(1 −cos ψ) +n
2
sin ψ,
R
23
= n
2
n
3
(1 −cos ψ) −n
1
sin ψ,
R
33
= n
2
3
+
1 −n
2
3
cos ψ.
The unit vector
ˆ
n ∈ S
2
can be further parametrized in
terms of the usual spherical polar coordinates:
ˆ
n =(sin θ cos φ, sin θ sin φ, cos θ) ,
0 ≤ θ ≤ π, 0 ≤φ<2π.
Euler angle parametrization:
U(αβγ) = e
−iασ
3
/2
e
−iβσ
2
/2
e
−iγσ
3
/2
=
e
−iα/2
cos
1
2
β
e
−iγ/2
−e
−iα/2
sin
1
2
β
e
iγ/2
e
iα/2
sin
1
2
β
e
−iγ/2
e
iα/2
cos
1
2
β
e
iγ/2
,
0 ≤ α<2π, 0 ≤β ≤ π or 2π ≤ β ≤3π,
0 ≤ γ<2π,
U(α, β +2π, γ) =−U(αβγ) ;
R(αβγ) = e
−iαM
3
e
−iβM
2
e
−iγM
3
=
cos α −sin α 0
sin α cos α 0
001
cos β 0sinβ
010
−sin β 0cosβ
×
cos γ −sin γ 0
sin γ cos γ 0
001
=
cos α cos β cos γ −cos α cos β sin γ cos α sin β
−sin α sin γ −sin α cos γ
sin α cos β cos γ −sin α cos β sin γ sin α sin β
+cos α sin γ +cos α cos γ
−sin β cos γ sin β sin γ cos β
0 ≤ α<2π, 0 ≤β ≤ π, 0 ≤γ<2π.
This matrix corresponds to the sequence of frame rota-
tions given by
rotate by γ about
ˆ
e
3
= (0, 0, 1),
rotate by β about
ˆ
e
2
= (0, 1, 0),
rotate by α about
ˆ
e
3
= (0, 0, 1).
Equivalently, it corresponds to the sequence of frame
rotations given by
rotate by α about
ˆ
n
1
= (0, 0, 1),
rotate by β about
ˆ
n
2
= (−sin α, cos α, 0),
rotate by γ about
ˆ
n
3
=
(cos α sin β, sin α sin β, cos β) .
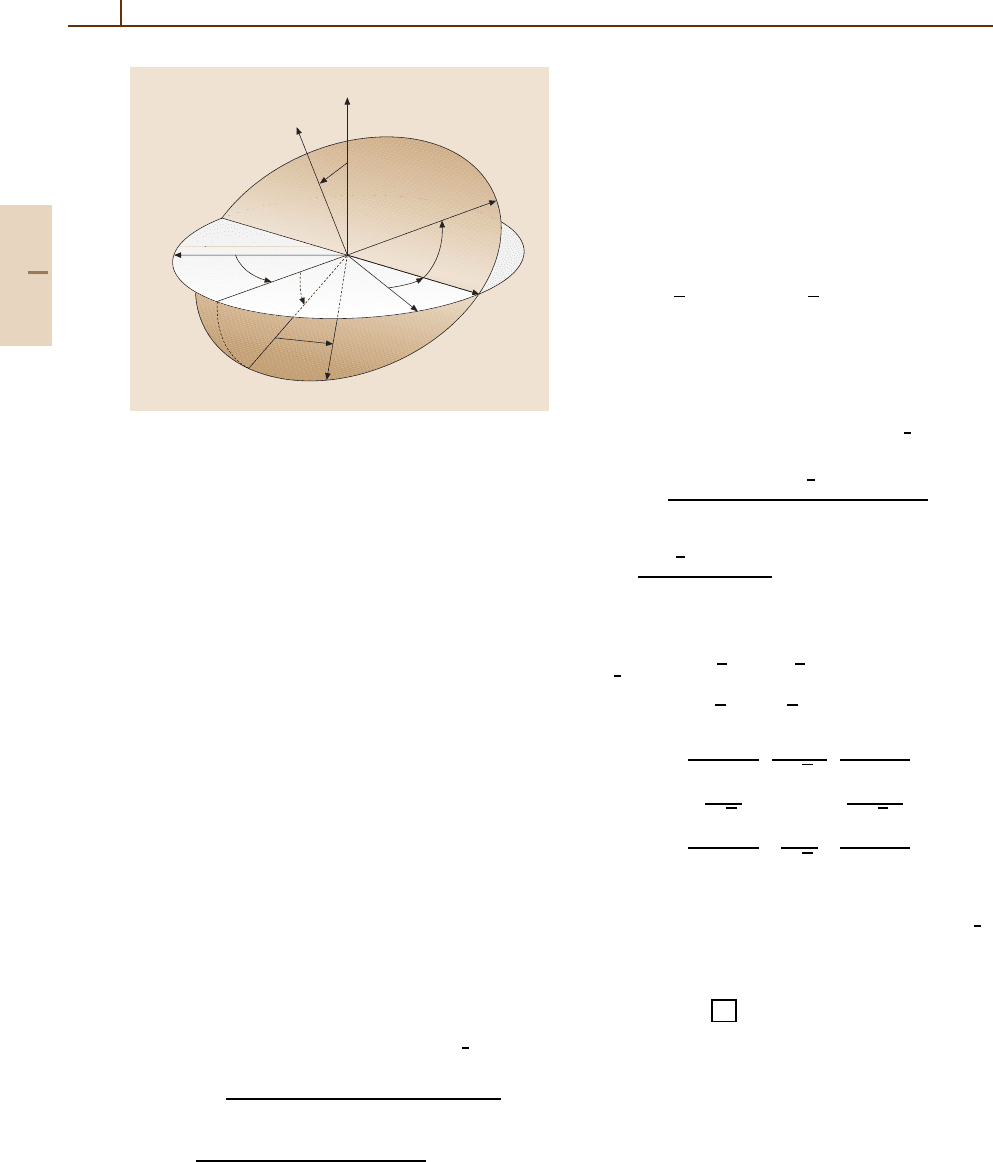
This latter sequence of rotations is depicted in Fig. 2.1
in obtaining the frame
ˆ
f
1
,
ˆ
f
2
,
ˆ
f
3
from (
ˆ
e
1
,
ˆ
e
2
,
ˆ
e
3
).
The four complex numbers
(a, b, c, d)
= (α
0
+iα
3
, iα
1
−α
2
, iα
1
+α
2
,α
0
−iα
3
)
Part A 2.3
20 Part A Mathematical Methods
β
β
α
α
γ
ˆ
n
3
=
ˆ
f
3
ˆ
e
3
=
ˆ
n
1
ˆ
e
1
ˆ
n
2
ˆ
f
2
ˆ
f
1
γ
ˆ
e
2
Fig. 2.1 Euler angles. The three Euler angles (αβγ )are
defined by a sequence of three rotations. Reprinted with the
permission of Cambridge University Press, after [2.1]
are called the Cayley–Klein parameters, whereas the
four real numbers (α
0
, α) defining a point on the sur-
face of the unit sphere in four-space, S
3
, are known as
the Euler–Rodrigues parameters. The three ratios α
i
/α
0
form the homogeneous or symmetric Euler parameters.
2.3.2 Explicit Forms
of Representation Functions
The general form of the representation functions is given
in its most basic and symmetric form in (2.17). This form
applies to every parametrization, it being necessary only
to introduce the explicit parametrizations of U ∈ SU(2)
or R ∈ SO(3, R) giveninSect.2.3.1 to obtain the explicit
results given in this section. A choice is also made for the
single independent summation parameter in the α-array.
The notation for functions is abused by writing
D
j
(ω) = D
j
(U(ω)) ,
ω = set of parameters of U ∈ SU(2).
Euler–Rodrigues representation
!
(α
0
, α) ∈ S
3
"
:
D
j
m
m
(α
0
, α)
=[( j +m
)!( j −m
)!( j +m)!( j −m)!]
1
2
×
s
(α
0
−iα
3
)
j+m−s
(−iα
1
−α
2
)
m
−m+s
( j +m −s)!(m
−m +s)!
×
(−iα
1
+α
2
)
s
(α
0
+iα
3
)
j−m
−s
s!( j −m
−s)!
.
(2.22)
Quaternionic multiplication rule for points on the
sphere S
3
:
α
0
, α
(α
0
, α) =
α
0
, α
,
α
0
= α
0
α
0
−α
·α ,
α
= α
0
α +α
0
α
+α
× α ;
D
j
α
0
, α
D
j
(α
0
, α) = D
j
α
0
, α
.
The (ψ,
ˆ
n) parameters:
α
0
= cos
1
2
ψ, α =
ˆ
nsin
1
2
ψ.
Euler angle parametrization:
D
j
m
m
(αβγ) = e
−im
α
d
j
m
m
(β) e
−imγ
,
d
j
m
m
(β) =jm
|e
−iβJ
2
|jm
=[( j +m
)!( j −m
)!( j +m)!( j −m)!]
1
2
×
s
(−1)
m
−m+s
cos
1
2
β
2 j+m−m
−2s
( j +m −s)!s!(m
−m +s)!
×
sin
1
2
β
m
−m+2s
( j −m
−s)!
.
(2.23)
Explicit matrices:
d
1
2
(β) =
cos
1
2
β −sin
1
2
β
sin
1
2
β cos
1
2
β
,
d
1
(β) =
1 +cos β
2
−sin β
√
2
1 −cos β
2
sin β
√
2
cos β
−sin β
√
2
1 −cos β
2
sin β
√
2
1 +cos β
2
.
Formal polynomial form (z
ij
are indeterminates):
D
j
m
m
(Z) =[( j +m
)!( j −m
)!( j +m)!( j −m)!]
1
2
×
α
2
i, j=1
(z
ij
)
α
ij
/(α
ij
)! , (2.24)
D
j
(Z
)D
j
(Z) = D
j
(Z
Z).
Boson operator form:
Put a
j
i
= z
ij
(i, j = 1, 2) in (2.24). Let
¯
a
j
i
denote the
Hermitian conjugate boson so that
#
a
k
l
, a
j
i
$
= 0 ,
#
¯
a
k
l
,
¯
a
j
i
$
= 0 ,
#
¯
a
k
l
, a
j
i
$
= δ
kj
δ
li
.
Part A 2.3
Angular Momentum Theory 2.3 Representation Functions 21
Then the boson polynomials are orthogonal in the boson
inner product:
0 | D
j
µ
µ
(
¯
A)D
j
m
m
(A) | 0=(2 j)!δ
j
j
δ
µ
m
δ
µm
.
2.3.3 Relations to Special Functions
Jacobi polynomials (see Sect. 2.1.2):
d
j
m
m
(β) =
( j +m)!( j −m)!
( j +m
)!( j −m
)!
1
2
sin
1
2
β
m−m
×
cos
1
2
β
m
+m
P
(m−m
,m+m
)
j−m
(cos β) ,
d
j
m
m
(β) = (−1)
m
−m
d
j
−m
,−m
(β)
= (−1)
m
−m
d
j
mm
(β) = d
j
mm
(−β) .
Legendre polynomials:
D
l
m0
(β) = (−1)
m
(l−m)!
(l+m)!
1
2
P
m
l
(cos β)
=
(l+m)!
(l−m)!
1
2
P
−m
l
(cos β) .
Spherical harmonics:
Y
lm
(βα) =
2l+1
4π
1
2
e
imα
d
l
m0
(β)
=
2l+1
4π
1
2
D
l∗
m0
(αβγ) ,
Y
∗
lm
(βα) = (−1)
m
Y
l,−m
(βα) .
Gegenbauer polynomials:
d
l
m0
(β) = (−1)
m
[(l+m)!(l−m)!]
1
2
×
(2m)!
m!
sin β
2
m
C
(m+1/2)
l−m
(cos β) ,
m ≥ 0 .
Solutions of Laplace’s equation in R
4
(Sect. 2.5):
∇
2
4
D
j
m
m
(x
0
, x) = 0 ,(x
0
, x) ∈ R
4
,
∇
2
4
=
3
µ=0
∂
2
∂x
2
µ
.
Replace the Euler–Rodrigues parameters (α
0
, α)
in (2.22) by an arbitrary point (x
0
, x) ∈ R
4
.
2.3.4 Orthogonality Properties
Inner (scalar) product:
(Ψ, Φ) =
dΩΨ
∗
(x)Φ(x),
dΩ = invariant surface measure for S
3
,
S
3
dΩ = 2π
2
.
Spherical polar coordinate for S
3
:
(α
0
, α) =
(cos χ, cos φ sin θ sin χ, sin φ sin θ sin χ, cos θ sin χ) ,
0 ≤ θ ≤ π, 0 ≤ φ<2π, 0 ≤χ ≤ π,
dΩ = dω sin
2
χ dχ,
dω = dφ sin θ,
dθ = invariant surface measure for S
2
;
2π
0
dφ
π
0
dθ sin θ
×
π
0
dχ sin
2
χ D
j∗
m
m
(α
0
, α)D
j
µ
µ
(α
0
, α)
=
2π
2
2 j +1
δ
jj
δ
m
µ
δ
mµ
.
Coordinates (ψ,
ˆ
n) for S
3
:
(α
0
, α) =
cos
ψ
2
,
ˆ
nsin
ψ
2
,
0 ≤ ψ ≤ 2π,
ˆ
n·
ˆ
n =1 ,
dΩ = dS(
ˆ
n) sin
2
ψ
2
dψ
2
,
dS(
ˆ
n) = dω
for
ˆ
n =(sin θ cos φ, sin θ sin φ, cos θ) ,
dS(
ˆ
n)
2π
0
dψ
2
sin
ψ
2
2
D
j∗
m
m
(ψ,
ˆ
n)D
j
µ
µ
(ψ,
ˆ
n)
=
2π
2
2 j +1
δ
jj
δ
m
µ
δ
mµ
,
Part A 2.3

22 Part A Mathematical Methods
Euler angles for S
3
(SU(2)):
(α
0
, α) =
cos
β
2
cos
1
2
(γ +α), sin
β
2
sin
1
2
(γ −α),
sin
β
2
cos
1
2
(γ −α), cos
β
2
sin
1
2
(γ +α)
,
dΩ =
1
8
dα dγ sin β dβ,
(2.25)
1
8
2π
0
dα
2π
0
dγ
π
0
dβ sin βD
j∗
m
m
(αβγ)D
j
µ
µ
(αβγ)
+
1
8
2π
0
dα
2π
0
dγ
3π
2π
dβ sin βD
j∗
m
m
(αβγ)D
j
µ
µ
(αβγ)
=
2π
2
2 j +1
δ
jj
δ
m
µ
δ
mµ
. (2.26)
Euler angles for hemisphere of S
3
(SO(3, R); j
and j
both integral):
2π
0
dα
2π
0
dγ
π
0
dβ sin βD
j∗
m
m
(αβγ)D
j
µ
µ
(αβγ)
=
8π
2
2 j +1
δ
jj
δ
m
µ
δ
mµ
. (2.27)
Formal polynomials (2.24):
D
j
m
m
, D
j
µ
µ
= (2 j)!δ
jj
δ
m
µ
δ
mµ
,
with inner product
(P, P
) = P
∗
∂
∂Z
P
(Z)|
Z=0
,
where P
∗
∂
∂Z
is the complex conjugate polynomial P
∗
of P in which each z
ij
is replaced by
∂
∂z
ij
.
Boson polynomials:
%
D
j
m
m
&
&
&
D
j
µ
µ
'
= (2 j)!δ
jj
δ
m
µ
δ
mµ
,
with inner product P|P
=0|P
∗
¯
A
P
(A)|0.
2.3.5 Recurrence Relations
Many useful relations between the representation func-
tions may be derived as special cases of general relations
between these functions and the WCG-coefficients given
in Sect. 2.7.1. The simplest of these are obtained from
the Kronecker reduction
D
j
× D
1
2
= D
j+1/2
⊕D
j−1/2
.
Such relations are usually presented in terms of the Euler
angle realization of U, leading to the following relations
between the functions d
j
m
,m
(β):
( j −m +1)
1
2
cos
1
2
β
d
j+1/2
m
−1/2,m−1/2
(β)
+( j +m +1)
1
2
sin
1
2
β
d
j+1/2
m
−1/2,m+1/2
(β)
= ( j −m
+1)
1
2
d
j
m
m
(β) ,
−( j −m +1)
1
2
sin
1
2
β
d
j+1/2
m
+1/2,m−1/2
(β)
+( j +m +1)
1
2
cos
1
2
β
d
j+1/2
m
+1/2,m+1/2
(β)
= ( j +m
+1)
1
2
d
j
m
m
(β) ,
( j +m)
1
2
cos
1
2
β
d
j−1/2
m
−1/2,m−1/2
(β)
−( j −m)
1
2
sin
1
2
β
d
j−1/2
m
−1/2,m+1/2
(β)
= ( j +m
)
1
2
d
j
m
m
(β) ,
( j +m)
1
2
sin
1
2
β
d
j−1/2
m
+1/2,m−1/2
(β)
+( j −m)
1
2
cos
1
2
β
d
j−1/2
m
+1/2,m+1/2
(β)
= ( j −m
)
1
2
d
j
m
m
(β) .
Two useful relations implied by the above are:
[
( j −m)( j +m +1)
]
1
2
sin β d
j
m
,m+1
(β)
+
[
( j +m)( j −m +1)
]
1
2
sin β d
j
m
,m−1
(β)
= 2(m cos β −m
)d
j
m
m
(β) ,
[
( j +m)( j −m +1)
]
1
2
d
j
m
,m−1
(β)
+
!
( j +m
)( j −m
+1)
"
1
2
d
j
m
−1,m
(β)
= (m −m
) cot
1
2
β
d
j
m
m
(β) .
By considering
D
j
× D
1
= D
j+1
⊕D
j
⊕D
j−1
,
one can also readily derive the matrix elements of the
direction cosines specifying the orientation of the body-
fixed frame
ˆ
f
1
,
ˆ
f
2
,
ˆ
f
3
of a symmetric rotor relative to
Part A 2.3

Angular Momentum Theory 2.3 Representation Functions 23
the inertial frame (
ˆ
e
1
,
ˆ
e
2
,
ˆ
e
3
):
λ
µ,ν
Ψ
j
m,m
=
j
2 j +1
2 j
+1
1
2
× C
j1 j
mµm+µ
C
j1 j
m
νm
+ν
Ψ
j
m+µ,m
+ν
,
where the wave functions are those defined for integral j
by (2.37), for half-integral j by (2.36), and
λ
µ,ν
=
ˆ
e
µ
·
ˆ
f
∗
ν
=
D
1
µ,ν
∗
,µ,ν=−1, 0, +1 ;
ˆ
e
+1
=−(
ˆ
e
1
+i
ˆ
e
2
)/
√
2 ,
ˆ
e
0
=
ˆ
e
3
,
ˆ
e
−1
= (
ˆ
e
1
−i
ˆ
e
2
)/
√
2 ,
ˆ
f
+
1
=−
ˆ
f
1
+i
ˆ
f
2
/
√
2 ,
ˆ
f
0
=
ˆ
f
3
,
ˆ
f
−
1
=
ˆ
f
1
−i
ˆ
f
2
/
√
2 .
2.3.6 Symmetry Relations
Symmetry relations for the representation functions
D
j
m
m
(Z) defined by (2.24) are associated with the action
of a finite group G on the set M(2, 2) of complex 2 × 2
matrices: g : M(2, 2) → M(2, 2), g ∈ G. Equivalently,
if Z ∈ M(2, 2) is parametrized by a set Ω of parameters
ω ∈Ω (parameter space), then g may be taken to act di-
rectly in the parameter space g : Ω →Ω. The action,
denoted
, of a group G ={e, g, g
,...} (e = identity)
on a set X ={x, x
,...} must satisfy the rules
g : X → X e
x = x, all x ∈ X ,
g
(g x) = (g
g) x, all g
, g ∈ G, all x ∈ X .
(2.28)
Using · to denote the action of G on M(2, 2) and to
denote the action of G on Ω, one has the relation:
(g· Z)(ω) = Z(g
−1
ω) .
Only finite subgroups G of the unitary group U(2)
(group of 2 × 2 unitary matrices) are considered here:
G ⊂ U(2).
Generally, when G acts on M(2, 2), it effects
a unitary linear transformation of the set of functions
(
D
j
m
m
)
( j fixed) defined over Z ∈ M(2, 2). For certain
groups G, or for some elements of G, a single function
D
j
µ
µ
∈
(
D
j
m
m
)
occurs in the transformation, so that
g· D
j
m
m
(Z) = D
j
m
m
(g
−1
Z)
= g
m
m
D
j
µ
µ
(Z), (2.29)
(µ
µ)
∈{(λ
m
,λm), (λm,λ
m
)|λ
=±1,λ=±1} ,
where g
m
m
is a complex number of unit modulus. Re-
lation (2.29) is called a symmetry relation of D
j
m
m
with
respect to g. Usually not all elements in G correspond
to symmetry relations. In a symmetry relation, the ac-
tion of the group is effectively transferred to the discrete
quantum labels themselves:
g : m
→ µ
= m
(g),
m → µ = m(g).
(2.30)
In terms of a parametrization Ω of M(2, 2), rela-
tion (2.29) is written
gD
j
m
m
(ω) = D
j
m
m
(g
−1
ω)
= g
m
m
D
j
µ
µ
(ω) . (2.31)
In practice, action symbols such as · and are often
dropped in favor of juxtaposition, when the context is
clear. Moreover the set of complex matrices M(2, 2)
may be replaced by U(2) or SU(2) whenever the action
conditions (2.28) are satisfied. Relations (2.29–2.31)are
illustrated below by examples.
There are several finite subgroups of interest with
various group-subgroup relations between them:
1. Pauli group:
P ={σ
µ
, −σ
µ
, iσ
µ
, −iσ
µ
|µ = 0, 1, 2, 3} ,
|P|=16 .
Each element of this group is an element of U(2).The
action of the group P may therefore be defined on
the group U(2) by left and right actions as discussed
in Sect. 2.4.1.
2. Symmetric groupS
4
:
S
4
={p|p is a permutation of the four Euler–
Rodrigues parameters (α
0
,α
1
,α
2
,σ
3
)},
&
&
S
4
&
&
= 24.
Points in S
3
are mapped to distinct points in S
3
;
hence, one can take Z ∈ SU(2), and define the group
action directly from U(α
0
, α) in (2.20). It is simpler,
however, to define the action of the group directly on
the representation functions (2.22). Not all elements
of this group define a symmetry in the sense defined
by (2.29)(seebelow).
3. Abelian group T:
T ={(t
0
, t
1
, t
2
, t
3
)| each t
µ
=±1} ,
|T|=16 .
Group multiplication is component-wise multipli-
cation and the identity is (1,1,1,1). The action
of an element of T is defined directly on the
Part A 2.3

24 Part A Mathematical Methods
Euler–Rodrigues parameters by component-wise
multiplication, thus mapping points in S
3
to points
in S
3
; hence, one can take Z ∈ SU(2). This group is
isomorphic to the direct product group S
2
× S
2
× S
2
× S
2
, S
2
=symmetric group on two distinct objects.
4. Group G:
G =R, C, T , K, |G|=32 ,
where R, C, T , K denote the operations of row in-
terchange, column interchange, transposition, and
conjugation (see below) of an arbitrary matrix.
Z =
ab
cd
The notation designates that the enclosed ele-
ments generate G.
It is impossible to give here all the interrelationships
among the groups defined in (1)–(4). Instead, some rela-
tions are listed as obtained directly from either D
j
m
m
(Z)
defined by (2.24)orD
j
m
m
(α
0
, α) defined by (2.22). The
actions of the groups T and G defined in (3) and (4) are
fully given.
Abelian group T of order 16:
Generators:
T =t
0
, t
1
, t
2
, t
3
, t
0
= (−1, 1, 1, 1),
t
1
= (1, −1, 1, 1), t
2
= (1, 1, −1, 1),
t
3
= (1, 1, 1, −1).
Group action:
t ·a = (t
0
α
0
, t
1
α
1
, t
2
α
2
, t
3
α
3
),
each t = (t
0
, t
1
, t
2
, t
3
) ∈ T ,
each a = (α
0
,α
1
,α
2
,α
3
) ∈ S
3
,
(tF)(a) = F(t ·a),
t
0
D
j
m
m
= (−1)
m
−m
D
j
−m−m
,
t
1
D
j
m
m
= (−1)
m
−m
D
j
mm
,
t
2
D
j
m
m
= D
j
mm
,
t
3
D
j
m
m
= D
j
−m−m
.
Group G of order 32:
Generators:
G =R, C, T , K ,
Generator actions:
(RF)
ab
cd
= F
cd
ab
,
row
interchange
(C F)
ab
cd
= F
ba
dc
,
column
interchange
(T F)
ab
cd
= F
ac
bd
, transposition
(K F)
ab
cd
= F
d −c
−ba
, conjugation
Subgroup H:
H =R, C, T
={1, R, C, T , RC = CR, TR=CT ,TC
= RT, RCT }
with relations in H given by
R
2
= C
2
= T
2
= 1 ,
TRC= TCR=RCT = CRT ,
RT C =CT R = T .
Adjoining the idempotent element K to H gives the
group G of order 32:
G ={H, HK, HKR, HKRK} .
Symmetry relations:
RD
j
m
m
= D
j
−m
m
,
C D
j
m
m
= D
j
m
−m
,
T D
j
m
m
= D
j
mm
,
K D
j
m
m
= (−1)
m
−m
D
j
−m
−m
. (2.32)
These function relations are valid for D
j
m
m
defined over
the arbitrary matrix Z defined by (2.24). They are also
true for Z = U ∈ SU(2), but now the operations R and
C change the sign of the determinant of the matrix Z so
that the transformed matrix no longer belongs to SU(2).
It does, however, belong to U(2), the group of all 2 × 2
unitary matrices. The special irreducible representation
functions of U(2) defined by (2.24),
D
j
m
m
(U), U ∈ U(2),
Part A 2.3

Angular Momentum Theory 2.4 Group and Lie Algebra Actions 25
possess each of the 32 symmetries corresponding to the
operations in the group G. [There exist other irreducible
representations of U(2), involving det U.] The opera-
tion K is closely related to complex conjugation, since
for each U ∈ U(2), U = (u
ij
), one can write
U
∗
= (det U)
−1
u
22
−u
21
−u
12
u
11
,
K D
j
m
m
(U) = (det U)
2 j
D
j
m
m
(U
∗
)
= (det U)
2 j
D
j∗
m
m
(U)
= (−1)
m
−m
D
j
−m
−m
(U). (2.33)
Relations (2.32)and(2.33) are valid in an arbi-
trary parametrization of U ∈ U(2).Intermsofthe
parametrization
U(χ, α
0
, α) = e
iχ/2
U(α
0
, α), 0 ≤ χ ≤2π,
where U(α
0
, α) ∈ SU(2) is the Euler–Rodrigues
parametrization, the actions of R , C, T ,andK cor-
respond to the following transformations in parameter
space:
R : χ →χ +π, (α
0
,α
1
,α
2
,α
3
)
→ (−α
1
,α
0
, −α
3
,α
2
),
C : χ → χ +π, (α
0
,α
1
,α
2
,α
3
)
→ (−α
1
,α
0
,α
3
, −α
2
),
T : χ →χ, (α
0
,α
1
,α
2
,α
3
) → (α
0
,α
1
, −α
2
,α
3
),
C : χ → χ, (α
0
,α
1
,α
2
,α
3
)
→ (α
0
, −α
1
,α
2
, −α
3
).
The new angle χ
= χ +π is to be identified with the
corresponding point on the unit circle so that these map-
pings are always in the parameter space, which is the
sphere S
3
together with the unit circle for χ. Observe that
the following identities hold for functions over SU(2);
hence, over U(2):
C = T
t
1
T
t
3
, T = T
t
2
.
Abelian subgroup of S
4
:
Generators:
K =(0, 3), (1, 2), where (0, 3) and (1, 2) denote
transpositions in S
4
, |K|=4.
Group action in parameter space:
(0, 3)(α
0
,α
1
,α
2
,α
3
) = (α
3
,α
1
,α
2
,α
0
),
(1, 2)(α
0
,α
1
,α
2
,α
3
) = (α
0
,α
2
,α
1
,α
3
).
Symmetry relations:
(0, 3)D
j
m
m
= (−i)
m
+m
D
j
−m−m
,
(1, 2)D
j
m
m
= (−i)
m
−m
D
j
mm
.
Diagonal subgroup Σ of the direct product group P × P
(P = Pauli group):
Group elements:
Σ ={(σ, σ)|σ ∈ P} ,
|
Σ
|
= 16 .
Group action:
(σ, σ) : U → σUσ
T
, each σ ∈ P ,
[
(σ, σ)F
]
(U) = F(σ
T
Uσ) .
Example: σ =iσ
2
:
(σ, σ) : (α
0
,α
1
,α
2
,α
3
) → (α
0
, −α
1
,α
2
, −α
3
),
[
(σ, σ)F
]
(α
0
,α
1
,α
2
,α
3
) = F(α
0
, −α
1
,α
2
, −α
3
),
(σ, σ) =t
1
t
2
on functions over U(2).
The relations presented above barely touch on
the interrelations among the finite groups introduced
in (1)–(4). Symmetry relations (2.32)and(2.33), how-
ever, give the symmetries of the d
j
m
m
(β) given
in Sect. 2.3.3 in the Euler angle parametrization. In gen-
eral, it is quite tedious to present the above symmetries in
terms of Euler angles, with χ adjoined when necessary,
because the Euler angles are not uniquely determined by
the points of S
3
.
2.4 Group and Lie Algebra Actions
The concept of a group acting on a set is funda-
mental to applications of group theory to physical
problems. Because of the unity that this notion brings
to angular momentum theory, it is well worth a brief
review in a setting in which a matrix group acts on
the set of complex matrices. Thus, let G ⊆ GL(n, C)
and H ⊆ GL(m, C) denote arbitrary subgroups, respec-
tively, of the general linear groups of n × n and m × m
nonsingular complex matrices, and let M(n, m) denote
the set of n×m complex matrices. A matrix Z ∈ M(n, m)
has row and column entries
z
α
i
, i = 1, 2,... ,n;
α = 1, 2,... ,m.
Part A 2.4
26 Part A Mathematical Methods
2.4.1 Matrix Group Actions
Left and right translations of Z ∈ M (n, m) :
L
g
Z = gZ , each g ∈ G , each Z ∈ M(n, m),
R
h
Z = Zh
T
, each h ∈ H , each Z ∈ M(n, m).
(T denotes matrix transposition.)
Left and right translations commute:
Z
= L
g
(R
h
Z) = R
h
(L
g
Z), each g ∈ G, h ∈ H ,
Z ∈ M(n, m).
Equivalent form as a transformation on z ∈ C
nm
:
z
= (g× h)z ,
where × denotes the direct product of gand h;thecolumn
matrix z (resp., z
) is obtained from the columns of Z
(resp., Z
), z
α
,α= 1, 2,... ,m, of the n × m matrix Z
as successive entries in a single column vector z ∈ C
nm
.
Left and right translations in function space:
(L
g
f )(Z) = f(g
T
Z), each g ∈ G ,
(R
h
f )(Z) = f(Zh), each h ∈ H ,
where f(Z) = f
z
α
i
, and the commuting property holds
for all well-defined functions f :
L
g
(R
h
f ) = R
h
(L
g
f ).
2.4.2 Lie Algebra Actions
Lie algebra of left and right translations:
(D
X
f )(Z) = i
d
dt
f
e
−itX
T
Z
|
t=0
,
(D
Y
f )(Z) = i
d
dt
f
Z e
−itY
|
t=0
;
D
X
= Tr
Z
T
X∂/∂Z
, each X ∈ L(G),
D
Y
= Tr
Y
T
Z
T
∂/∂Z
, each Y ∈ L(H),
L(G) =Lie algebra of G ,
L(H) =Lie algebra of H .
Linear derivations:
D
αX+βX
= αD
X
+βD
X
,α,β∈ C ,
[
D
X
, D
X
]
= D
[X,X
]
,
D
Y
obeys these same rules.
Commuting property of left and right derivations:
!
D
X
, D
Y
"
= 0 , X ∈ L(G), Y ∈ L(H).
Basis set:
D
X
=
n
i, j=1
x
ij
D
ij
, X = (x
ij
),
D
Y
=
m
α,β=1
y
αβ
D
αβ
, Y = (y
αβ
),
D
ij
=
m
α=1
z
α
i
∂
∂z
α
j
,
D
αβ
=
n
i=1
z
α
i
∂
∂z
β
i
.
Commutation rules:
[D
ij
, D
kl
]=δ
jk
D
il
−δ
il
D
kj
,
[D
αβ
, D
γ
]=δ
βγ
D
α
−δ
α
D
γβ
,
[D
ij
, D
αβ
]=0 ,
where i, j, k, l=1, 2,... ,n and α,β,γ, =1, 2,... ,m.
The operator sets {D
ij
} and {D
αβ
} are realizations
of the Weyl generators of GL(n, C) and GL(m, C),
respectively.
2.4.3 Hilbert Spaces
Space of polynomials with inner product:
(P, P
) = P
∗
(∂/∂Z)P
(Z)|
Z=0
.
Bargmann space of entire functions with inner product:
F, F
=
F
∗
(Z)F
(Z) dµ(Z),
dµ(Z) = π
−nm
exp
−
i,α
z
α∗
i
z
α
i
i,α
dx
α
i
dy
α
i
,
z
α
i
= x
α
i
+iy
α
i
, i = 1, 2,... ,n ; α = 1, 2,... ,m .
Numerical equality of inner products:
(P, P
) =P, P
.
2.4.4 Relation
to Angular Momentum Theory
Spinorial Realization of Sects. 2.4.2 and 2.4.3:
G = SU(2), H = (1), Z ∈ M (2, 1),
z = col(z
1
, z
2
),
X = set of 2 × 2 traceless, Hermitian matrices,
(R
U
f )(z) = f(U
T
z),
D
σ
i
/2
= (z
T
σ
i
∂/∂z)/2 ,
Part A 2.4
Angular Momentum Theory 2.4 Group and Lie Algebra Actions 27
J
±
= D
σ
1
/2
±iD
σ
2
/2
, J
3
= D
σ
3
/2
,
J
+
= z
1
∂/∂z
2
, J
−
= z
2
∂/∂z
1
,
J
3
= (1/2)(z
1
∂/∂z
1
−z
2
∂/∂z
2
),
(P, P
) = P
∗
(∂/∂z
1
,∂/∂z
2
)P(z
1
, z
2
)|
z
1
=z
2
=0
.
Orthonormal basis:
P
jm
(z
1
, z
2
) = z
j+m
1
z
j−m
2
/[( j +m)!( j −m)!]
1
2
,
j = 0, 1/2, 1, 3/2,... ; m = j, j −1,... ,−j .
Standard action:
J
2
P
jm
(z) = j( j +1)P
jm
(z),
J
3
P
jm
(z) =mP
jm
(z),
J
±
P
jm
(z) =[( j ∓m)( j ±m +1)]
1
2
P
j,m±1
(z).
Group transformation:
(R
U
P
jm
)(z) =
m
D
j
m
m
(U)P
jm
(z),
where the representation functions are given by (2.17).
The 2-Spinorial Realization of Sects. 2.4.2
and 2.4.3:
G = H = SU(2), Z ∈ M(2, 2),
Z =
!
z
1
z
2
"
, z
α
= col
z
α
1
z
α
2
,
X = Y = set of 2 × 2 traceless, Hermitian matrices ,
(R
U
f )(Z) = f(U
T
Z), (L
V
f )(Z) = f(ZV ),
U, V ∈ SU(2),
D
σ
i
/2
= Tr(Z
T
σ
i
∂/∂Z)/2 ,
D
σ
i
/2
= Tr(σ
i
Z
T
∂/∂Z)/2 .
M
±
= D
σ
1
/2
±iD
σ
2
/2
, M
3
= D
σ
3
/2
,
K
±
= D
σ
1
/2
±iD
σ
2
/2
, K
3
= D
σ
3
/2
,
M
+
=
2
α=1
z
α
1
∂/∂z
α
2
, M
−
=
2
α=1
z
α
2
∂/∂z
α
1
,
M
3
=
1
2
2
α=1
z
α
1
∂/∂z
α
1
−z
α
2
∂/∂z
α
2
,
K
+
=
2
i=1
z
1
i
∂/∂z
2
i
, K
−
=
2
i=1
z
2
i
∂/∂z
1
i
,
K
3
=
1
2
2
i=1
z
1
i
∂/∂z
1
i
−z
2
i
∂/∂z
2
i
.
Mutual commutativity of Lie algebras:
[M
i
, K
j
]=0 , i, j = 1, 2, 3 .
Inner product:
(P, P
) = P
∗
(Z)P
(∂/∂Z)|
Z=0
,
Orthogonal basis (2.24):
D
j
mm
(Z), j = 0, 1/2, 1, 3/2,... ,
m = j, j −1,... ,−j ;
m
= j, j −1,... ,−j ;
D
j
mm
, D
j
µµ
= (2 j)!δ
jj
δ
mµ
δ
m
µ
.
Equality of Casimir operators:
M
2
= K
2
= M
2
1
+M
2
2
+M
2
3
= K
2
1
+K
2
2
+K
2
3
.
Standard actions:
M
2
D
j
mm
(Z) = K
2
D
j
mm
(Z) = j( j +1)D
j
mm
(Z),
M
3
D
j
mm
(Z) = mD
j
mm
(Z),
K
3
D
j
mm
(Z) = m
D
j
mm
(Z),
M
±
D
j
mm
(Z) =[( j ∓m)( j ±m +1)]
1
2
D
j
m±1,m
(Z),
K
±
D
j
mm
(Z) =[( j ∓m
)( j ±m
+1)]
1
2
× D
j
m,m
±1
(Z).
Special values:
D
j
10
01
= I
2 j+1
= unit matrix ,
D
j
mm
z
1
0
z
2
0
= δ
jm
P
jm
(z
1
, z
2
),
D
j
mm
0 z
1
0 z
2
= δ
jm
P
jm
(z
1
, z
2
),
D
j
mm
z
1
0
0 z
2
= δ
mm
z
j+m
1
z
j−m
2
,
D
j
jj
(Z) =
z
1
1
2 j
.
Part A 2.4
