Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics

Подождите немного. Документ загружается.

List of Abbreviations

2P/2H two-particle/two-hole

AA average atom

ACT activated complex theory

ADDS angular distribution by Doppler

spectroscopy

ADO average dipole orientation

AES Auger electron spectroscopy

AI adiabatic ionization

AL absorption loss

ALS advanced light source

AMO atomic, molecular, and optical

ANDC arbitrarily normalized decay curve

AO atomic orbital

AOM acoustooptic modulator

AS active space

ASD atomic spectra database

ASF atomic state functions

ATI above threshold ionization

AU absorbance units

BEA binary encounter approximation

BEC Bose–Einstein condensate

(or condensation)

BF body-ﬁxed

BI Bell’s inequality

BL Bethe log

BO Born–Oppenheimer

BS Bethe–Salpeter

BW Brillouin–Wigner

CARS coherent anti-Stokes Raman scattering

CAS complete active space

CASPT complete active space perturbation

theory

CAUGA Clifford algebra unitary group approach

CC coupled cluster

CCA coupled cluster approximation

CCC convergent close coupling

CCD coupled cluster doubles

CCO coupled-channels optical

CDW continuum distorted wave

CEAS cavity enhanced absorption spectroscopy

CES cavity enhanced spectroscopy

CES constant energy surface

CETS cavity enhanced transmission

spectroscopy

CFCP free–free molecular Franck–Condon

CG Clebsch–Gordan

CH Clauser–Horne

CI conﬁguration interaction

CIS constant ionic state

CL constant log

CM center-of-mass

CMA cylindrical mirror analyzer

COA classical oscillator approximation

CODATA Committee on Data for Science and

Technology

COIL chemical-oxygen-iodine

COLTRIMS cold-target recoil-ion momentum

spectroscopy

CP central potential

CPA chirped-pulsed-ampliﬁcation

CQC classical-quantal coupling

CRDS cavity ring-down spectroscopy

CSDA continuous slowing down approximation

CSF conﬁgurational state functions

CTF common translation factor

CTMC classical trajectory Monte Carlo

CW continuous wave

CW-CRDS continuous-Wave Cavity Ring-Down

Spectroscopy

CX charge exchange

CXO Chandra X-ray Observatory

DB detailed balance

DCS differential cross sections

DDCS doubly differential cross sections

DF Dirac–Fock

DFB distributed feedback

DFS decoherence free subspace

DFT discrete Fourier transform

DFWM degenerate four wave mixing

DLR dielectronic recombination

DODS different orbitals for different spins

DR dielectronic recombination

DSPB distorted wave strong potential Born

approximation

EA excitation-autoionization

EBIT electron beam ion traps

EBS eikonal Born series

LVI List of Abbreviations

ECP effective core potential

ECS exterior complex scaling

EEDF electron energy distribution functions

EOM equation of motion

EPR Einstein–Podolsky–Rosen

ESM elastic scattering model

ESR experimental storage ring

EUV extreme ultraviolet

EW-CRDS evanescent-wave CRDS

EXAFS extended X-ray absorption ﬁne structure

FBA ﬁrst Born approximation

FCPC full-core plus correlation

FEL free-electron lasers

FFT fast Fourier transform

FID free induction decay

FIR far-infrared

FM frequency modulation

FOTOS ﬁrst-order theory for oscillator strengths

FS ﬁne-structure

FT Fourier transform

FTIR Fourier transform infrared spectroscopy

FTMS Fourier transform mass spectrometry

FTS Fourier transform spectroscopy

FUSE far ultraviolet spectroscopic explorer

FUV far ultraviolet

FVP Fermi virtual photon

FWHM full width at half maximum

GBT generalized Brillouin’s Theorem

GFA Green’s function approach

GGA generalized gradient approximation

GHZ Greenberger, Horne, Zeilinger

GI gauge invariant

GIB guided ion beam

GOME global ozone monitoring experiment

GOS generalized oscillator strength

GPE Gross–Pitaevskii equation

GRPAE generalized random phase

approximationwith exchange

HEDP high energy-density physics

HF Hartree–Fock equations

HF Hellman–Feynman

HG harmonic generation

HOM Hong–Ou–Mandel

HREELS high resolution electron energy loss

spectroscopy

HRTOF H-atom Rydberg time-of-ﬂight

HUM Hylleraas–Undheim–MacDonald

theorem

IC intermediate coupling

ICF inertial conﬁnement fusion

ICOS integrated cavity output spectroscopy

ICSLS international conference on spectral line

shapes

IERM intermediate energy R-matrix

IPCC intergovernmental panel on climate

change

IPES inverse photoemission spectroscopy

IPIR independent-processes and

isolated-resonance

IPM independent particle model

IPP impact parameter picture

IR irreducible representations

IR infrared

IRI international reference ionosphere

IRREP irreducable representation

ISO infrared space observatory

JB Jeffrey–Born

KS Kohn–Sham

KTA potassium titanyl arsenate

KTP potassium titanyl phosphate

LieA Lie algebras

LA linear algebraic

L-CETS locked cavity enhanced transmission

spectroscopy

LDA local density approximation

LEED low energy electron diffraction

LER laser electric resonance

LG Lie groups

LHC left-hand circular

LHV local hidden variable

LIF laser-induced-ﬂuorescence

LIGO laser interferometer gravitational-wave

observatory

LISA laser interferometer space antenna

LL Landau–Lifshitz

LM Levenberg–Marquardt

LMR laser magnetic resonance

LPT laser photodetachment threshold

LRL Laplace–Runge–Lenz

LTE local thermodynamic

equilibrium

LYP Lee, Yang, and Parr

LZ Landau–Zener

List of Abbreviations LVII

MBE molecular beam epitaxy

MCP microchannel plate

MDAL minimum detectable absorption loss

MBPT many-body perturbation theory

MCDHF multiconﬁgurational Dirac–Hartree–Fock

MCHF multiconﬁguration Hartree–Fock

MCSCF multiconﬁgurational self-consistent ﬁeld

MEMS microelectromechanical systems

MFP mean free path

MIGO matter–wave interferometric

gravitational-wave observatory

MIM metal-insulator-metal

MKSA meters, kilograms, seconds, and amperes

MM Massey–Mohr

MMCDF multichannel multiconﬁguration

Dirac–Fock

MO molecular orbital

MOPA master oscillator power ampliﬁer

MOT magneto-optical trap

MOX molecular orbital X-radiation

MP2 second order Møller–Plesset perturbation

theory

MP3 third order Møller–Plesset perturbation

theory

MPI multiphoton ionization

MQDT multichannel quantum defect theory

MR multireference

MR-SDCI multireference singles/doubles

conﬁguration interaction

MUV middle ultraviolet

NAR nonadiabatic region

NEP noise-equivalent power

NEXAFS near-edge X-ray absorption ﬁne structure

NDIR non-dispersive infrared

NFS nonﬁne-structure

NICE-OHMS noise-immune, cavity-enhanced optical

heterodyne molecular spectroscopy

NIM normal incidence monochromator

NIST National Institute of Standards and

Technology

NMR nuclear magnetic resonance systems

NNS nearest-neighbor energy level spacings

NR nonrelativistic

NRQED NR quantum electrodynamics

OAO-2 orbiting astronomical observatory

OB ordinary Bremsstrahlung

OBE optical Bloch equations

OBK Oppenheimer–Brinkman–Kramers

OCP one-component plasma

OHCE one-and-a-half centered expansion

OMI ozone monitoring instrument

OPO optical parametric oscillator

P-CRDS pulsed-cavity ringdown spectroscopy

PADDS angular distribution by Doppler

spectroscopy

PAH polycyclic aromatic hydrocarbon

PBS polarizing beam splitters

PCDW projectile continuum distorted wave

approximation

PDM phase diffusion model

PEC potential energy curves

PES photoelectron spectroscopy

PES potential energy surface

PH/HP particle–hole/hole–particle

PI photoionization

PID particle identiﬁcation

PIMC path-integral Monte Carlo

PMT photomultiplier tubes

PNC parity nonconservation

PPT positive partial transposes

PR polarization radiation

PSD postion senitive detectors

PSS perturbed stationary state

PT perturbation theory

PWBA plane wave Born approximation

PZT piezo-electric transducer

QCD quantum chromodynamics

QED quantum electrodynamics

QIP quantum information processing

QKD quantum key distribution

QMC quantum Monte Carlo

QND quantum nondemolition

QS quasistatic

QSS quasi-steady state

RATIP relativistic atomic transition and

ionization properties

RDC ring-down cavity

READI resonant excitation auto-double ionization

REC radiative electron capture

REDA resonant excitation double autoionization

REMPI resonance-enhanced multiphoton

ionization

RES rotational energy surface

RHC right-hand circular

RHIC relativistic heavy ion collider

LVIII List of Abbreviations

RIMS recoil-ion momentum spectroscopy

RMI relativistic mass increase

RMPS R-matrix with pseudostates

RNA Raman–Nath approximation

RPA random-phase approximation

RPA retarding potential analyzer

RPAE random phase approximation with

exchange

RR radiative recombination

RRKM Rampsberger–Rice–Karplus–Marcus

RSE radial Schrödinger equation

RSPT Rayleigh–Schrödinger perturbation

theory

RT Ramsauer–Townsend

RTE resonant transfer and excitation

RWA rotating wave approximation

SA-MCSCF state averaged multiconﬁguration

self-consistent ﬁeld

SACM statistical adiabatic channel model

SBS stimulated Brillouin scattering

SCA semiclassical approximation

SCF self-consistent ﬁeld

SCIAMACHY scanning imaging absorption

spectrometer for atmospheric

chartography

SD spin-dependent

SD single and double

SDS singly differential cross section

SDTQ single, double, triple, quadruple

SE Schrödinger equation

SEP stimulated emission pump

SEPE simultaneous electron photon

excitation

SEXAFS surface extended X-ray absorption ﬁne

structure

SF space-ﬁxed

SI spin-independent

SIAM Society for Industrial and Applied

Mathematics

SM submillimeter

SM-FIR submillimeter far-infrared

SMS speciﬁc mass shift

SOHO solar and heliospheric observatory

SP stationary phase

SPA stationary phase approximations

SQL standard quantum limit

SQUID superconducting quantum interference

detector

SR synchrotron radiation

SRS stimulated Raman scattering

SS strong-short

STIRAP stimulated Raman adiabatic passage

STO Slater type orbital

STP standard temperature and pressure

TCDW target continuum distorted wave

TDCS triply differential cross section

TDHF time-dependent Hartree–Fock

TDS thermal desorption spectroscopy

TDSE time dependent Schrödinger equation

TEA transverse-excitation-atmospheric-

pressure

TF toroidal ﬁeld

TOF time-of-ﬂight

TOP time orbiting potential

TPA two-photon absorption

TSR test storage ring

TuFIR tunable far-infrared

UGA unitary group approach

UHF unrestricted Hartree–Fock

UPS ultraviolet photoelectron spectroscopy

UV ultraviolet

UV-VIS ultraviolet-visible

VASP Vienna ab-initio simulation package

VCSEL vertical-cavity surface-emitting laser

VECSEL vertical external cavity surface-emitting

laser

VES vibrational energy surfaces

VUV vacuum ultraviolet

WCG Wigner–Clebsch–Gordan

WDM warm dense matter

WKB Wentzel, Kramers, Brillouin

WL weak-long

WMAP Wilkinson microwave anisotropy

probe

WPMD wavepacket molecular dynamics

XPS X-ray photoelectron spectroscopy

YAG Yttrium Aluminum Garnet

Units and Con

1. Units and Constants

The currently accepted values for the physi-

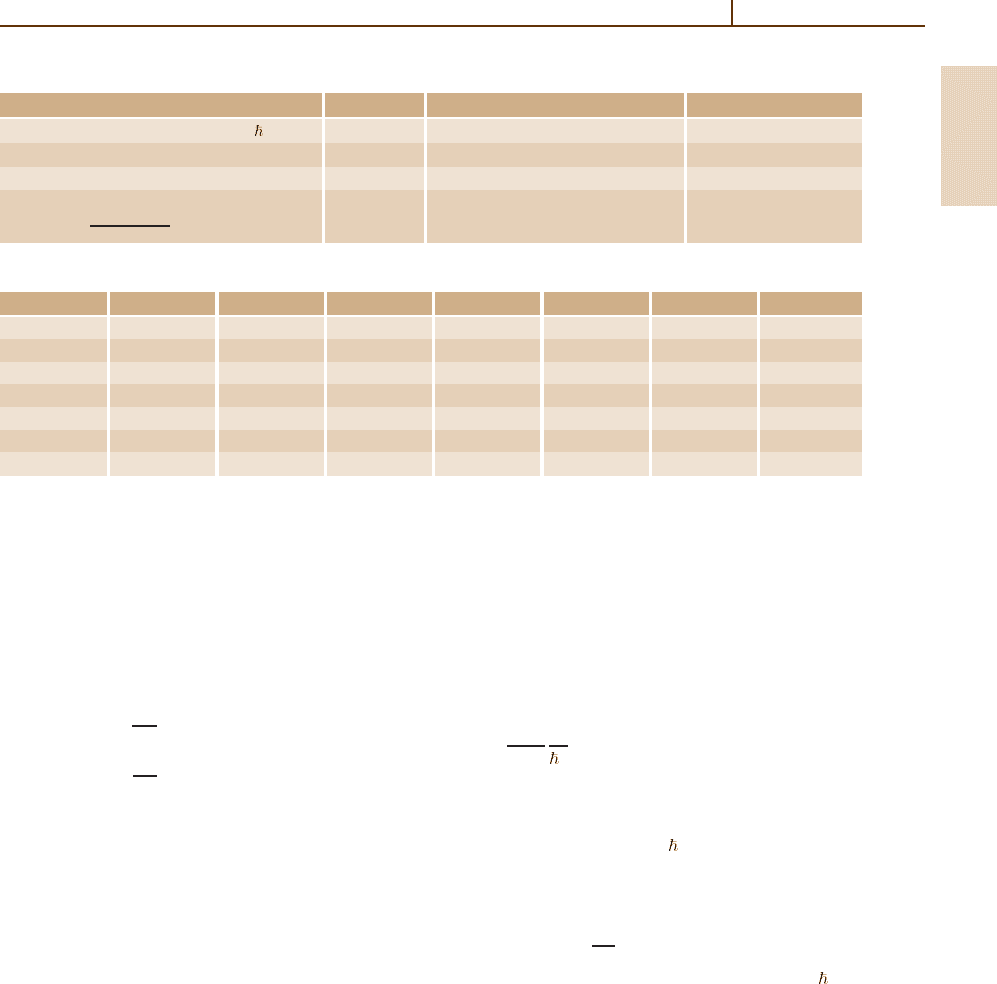
cal constants are listed in Table 1.1,basedon

the 2002 CODATA (Committee on Data for Sci-

ence and Technology) recommendations [1.1].

The quoted values are based on all data avail-

able through 31 December 2002, and replace

the earlier 1998 CODATA set. Because the uncer-

tainties are correlated, the correlation matrix,

given in Table 1.2, must be used in calculating

1.1 Electromagnetic Units .......................... 1

1.2 Atomic Units ....................................... 5

1.3 Mathematical Constants ....................... 5

1.3.1 Series Summation Formula ......... 5

References .................................................. 6

uncertainties for any quantities derived from those

tabulated [1.1].

1.1 Electromagnetic Units

The standard electromagnetic units adopted by most

scientiﬁc journals and elementary texts belong to the

système international (SI) or rationalized MKSA (me-

ters, kilograms, seconds, and amperes) units. However,

many authors working with microscopic phenomena

prefer Gaussian units, and theoretical physicists often

use Heaviside–Lorentz (H–L) units. In this Handbook,

SI units are used together with atomic units. The current

section is meant as a reference relating these different

systems.

The relations among different sets of units are not

simple conversions since the same symbol in differ-

ent systems can have different physical dimensions. To

clarify the meanings of the units, we summarize ba-

sic electromagnetic relations for SI, Gaussian, and H–L

systems below.

The Coulomb law for the magnitude F of the force

acting on each of two static charges q and Q separated by

a distance r in a homogeneous medium of permittivity

 can be written as

F =

4π

, (1.1)

where in a vacuum,  is

















−1

, SI

(4π)

−1

, Gaussian

1, H–L

(1.2)

with the closely related permeability of vacuum given











4π ×10

−7

N/A

, SI

4π, Gaussian

1, H–L

(1.3)

(We deviate here from Jackson [1.2]whotakes

= 1 in Gaussian units and must introduce additional

constants to relate the units. The physically important

quantities are the relative values 

≡ /

and µ

≡

µ/µ

, which in traditional Gaussian-unit notation are

written without the r subscript.)

Note that 

and µ

are dimensionless in H–L and

Gaussian units, but not in the SI units. Current or electric

charge is an independent quantity in the MKSA system

but can be expressed in purely mechanical dimensions in

the H–L and Gaussian systems. Thus, in Gaussian units,

1 statcoulomb = 1 dyne

(1/2)

cm, but in SI, even though

theampereisdeﬁned in terms of the attractive force be-

tween thin parallel wires carrying equal currents, there is

no mechanical equivalent for the ampere or the coulomb.

To establish such an equivalence, one can supplement

the SI units by assigning a dimensionless number to 

or to µ

. Gaussian and H–L units arise from two differ-

ent assignments. The result of assigning a number to 

is analogous to the relation 1 s =

3×10

m established

between time and distance units if one sets the speed of

light c =1, a convention often used in conjunction with

H–L units. (Note that for simplicity, the pure number

Introduction

2 Part

Table 1.1 Table of physical constants. Uncertainties are given in parentheses

Quantity Symbol Value Units

Speed of light in vacuum c 2.997 924 58 10

−1

Gravitational constant G 6.6742(10) 10

−11

−1

−2

Planck constant h 6.626 0693(11) 10

−34

= h/2π 1.054 571 68(18) 10

−34

Elementary charge e 1.602 176 53(14) 10

−19

4.803 204 40(42) 10

−10

esu

Inverse ﬁne structure constant [4π

] c/e

−1

137.035 999 11(46)

Magnetic ﬂux quantum h/2e Φ

2.067 833 72(18) 10

−15

Atomic mass constant





= 1u m

1.660 538 86(28) 10

−27

931.494 043(80) MeV

Electron mass m

9.109 3826(16) 10

−31

5.485 799 0945(24) 10

−4

Muon mass m

0.113 428 9264(30) u

Proton mass m

1.007 276 466 88(13) u

Neutron mass m

1.008 664 915 60(55) u

Deuteron mass m

2.013 553 212 70(35) u

α-particle mass m

4.001 506 179 149(56) u

Rydberg constant m

cα

2h R

∞

1.097 373 156 8525(73) 10

−1

∞

c 3.289 841 960 360(22) 10

∞

hc 13.605 692 3(12) eV

2.179 872 09(37) 10

−18

Bohr radius α/4πR

∞

0.529 177 2108(18) 10

−10

Hartree energy e

/[4π

= 2R

∞

hc E

27.211 3845(23) eV

/h 6.579 683 920 721(44) 10

/hc 2.194 746 313 705(15) 10

−1

Compton wavelength αa

= λ

/2π 3.861 592 678(26) 10

−13

Classical electron radius α

2.817 940 325(28) 10

−15

Thomson cross section 8πr

/3 σ

0.665 245 873(13) 10

−28

Bohr magneton [c]e /2m

c µ

9.274 009 49(80) 10

−24

−1

5.788 381 804(39) 10

−5

eV T

−1

Electron magnetic moment µ

/µ

−1.001 159 652 1859(38)

Muon magnetic moment µ

/µ

−4.841 970 45(13) 10

−3

Proton magnetic moment µ

/µ

1.521 032 206(15) 10

−3

Neutron magnetic moment µ

/µ

−1.041 875 63(25) 10

−3

Deuteron magnetic moment µ

/µ

0.466 975 4567(50) 10

−3

Electron g factor −2(1 +a

) g

−2.002 319 304 3718(75)

Muon g factor −2(1 +a

) g

−2.002 331 8396(12)

Proton gyromagnetic ratio 2µ

/ γ

2.675 222 05(23) 10

−1

Avogadro constant N

6.022 1415(10) 10

mol

−1

Faraday constant N

e F 9.648 533 83(83) 10

Cmol

−1

Boltzmann constant R/N

1.380 6505(24) 10

−23

−1

8.617 343(15) 10

−5

eV K

−1

3.166 8153(55) 10

−6

−1

Molar gas constant R 8.314 472(15) Jmol

−1

Molar volume (ideal gas) RT/P

T = 273.15 K, P =101.325 kPa V

0.022 413 996(39) m

mol

−1

T = 273.15 K, P =100 kPa V

0.022 710 981(40) m

mol

−1

Introduction

Units and Constants 1.1 Electromagnetic Units 3

Table 1.1 Table of physical constants. Uncertainties are given in parentheses, cont.

Quantity Symbol Value Units

Stefan–Boltzmann constant π

/(60

) σ 5.670 400(40) 10

−8

−2

−4

First radiation constant 2πhc

3.741 771 38(64) 10

−16

Second radiation constant hc/k

0.014 387 752(25) mK

Wien displacement law constant b 2.897 7685(51) 10

−3

max

T =

4.965 114 231...

Table 1.2 The correlation coefﬁcients of a selected group of constants based on the 2002 CODATA [1.1]

α h e m

α − − − − − − −

h 0.010 − − − − − −

e 0.029 1.000 − − − − −

−0.029 0.999 0.998 − − − −

0.029 −0.999 −0.998 −1.000 − − −

−0.249 −0.002 −0.007 0.007 −0.007 − −

F 0.087 −0.995 −0.993 −0.998 0.998 −0.022 −

2.997 924 58, equal numerically to the deﬁned speed of

light in vacuum in units of 10

m/s, is represented by

3.)

Thus, although within the Gaussian system, where the

assignment 4π

= 1 is made, it is justiﬁed to assert that

1 coulomb equals

3×10

statcoulombs, this is not true

in pure SI, where there is no equivalent mechanical unit

for charge.

Maxwell’s macroscopic equations can be written as

λ∇·D = ρ,

λc



∇× H−λ

∂ D

∂t

= j ,



∇× E+

∂ B

∂t

= 0 ,

∇·B = 0 ,

(1.4)

with the macroscopic ﬁeld variables related to the polar-

izations P and M by

λD = 

E+ P = E

λH =µ

−1

B− M = B/µ (1.5)

(the last equalities for D and H hold only for homoge-

neous media) and

λ =







1, SI



= µ

−1

, Gaussian or H–L ,

(1.6)









1, SI

c, Gaussian or H–L .

(1.7)

In Gaussian or H–L units, the ﬁelds E, B, D, H,

and polarizations (dipole moments per unit volume)

P, M all have the same dimensions, whereas in SI

units the microscopic ﬁelds E and B have dimensions

that are generally distinct from each other as well as

from P (or D)andM (or H), respectively. In all three

unit systems, the dimensionless ratio /

is called

the dielectric constant (or relative permittivity) of the

medium, and the (dimensionless) ﬁne-structure constant

α =

4π

(1.8)

with a numerical value α

−1

= 137.035 999 11 (46).

In atomic units (Sect. 1.3), the factor e

(

4π

)

the electron mass m

,and , Planck’s constant di-

vided by 2π, are all equal to 1. In Gaussian and

H–L systems, these conditions determine a numerical

value for all electro-mechanical units. Thus in Gaussian

units, the electronic charge is e = 1, whereas in H–L

atomic units e =

√

4π. In the SI system, on the other

hand, the three conditions e

(

4π

)

= m

= = 1

determine numerical values for mechanical units but

not for electromagnetic ones. A complete determi-

nation of values requires that 

also be assigned

a value. The choice most consistent with previous

work is to take e = 1 = 4π

. This choice is made

here.

Since a volt is a joule/coulomb and a statvolt is

an erg/statcoulomb, 1 volt corresponds to (but is not

generally equal to, since the physical dimensions may

Introduction

4 Part

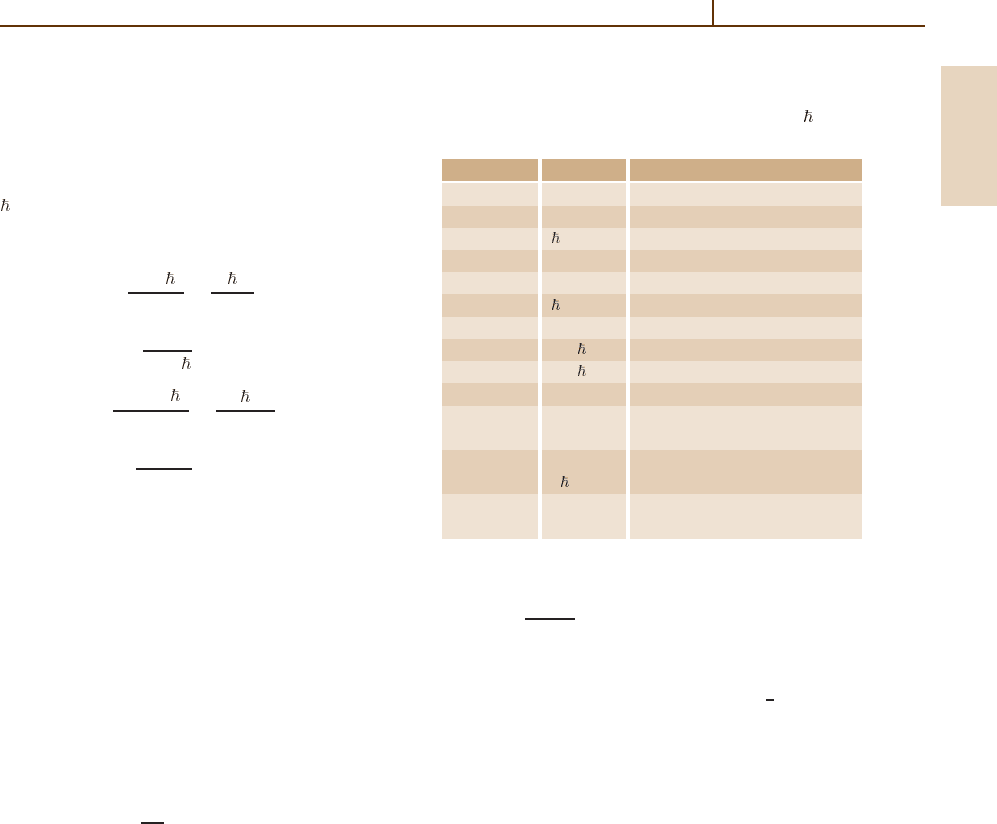
Table 1.3 Conversion factors for various physical quantities

Quantity SI units Gaussian units Natural H–L units: = c = 

= 1

Length 1m = 10

cm = 1m

Mass 1kg = 10

g ↔ 2.842 788 82(49) × 10

−1

Time 1s = 1s ↔

×10

Velocity 1ms

−1

= 10

cm s

−1

↔

−1

×10

−8

Energy 1J= 1kgm

−2

= 10

erg ↔ 3.163 029 14(54) ×10

−1

Action 1Js = 10

erg s ↔ 0.948 252 28(16) ×10

Force 1N= 1Jm

−1

= 10

dyne ↔3.163 029 14(54) ×10

−2

Power 1W= 1Js

−1

= 10

erg s

−1

↔ 1.055 072 95(18) ×10

−2

Intensity 1Wm

−2

= 10

erg cm

−2

↔ 1.055 072 95(18) ×10

−4

Charge 1C= 1As ↔

×10

statcoul ↔ 1.890 067 14(16) ×10

Potential 1V= 1JC

−1

↔ (

×10

)

−1

statvolt ↔ 1.673 500 94(14) ×10

−1

Electric ﬁeld 1Vm

−1

= 1NC

−1

↔ (

×10

)

−1

statvolt cm

−1

↔ 1.673 500 94(14) ×10

−2

Magnetic ﬁeld 1T= 1NA

−1

↔ 10

gauss ↔ 5.017 029 61(43) ×10

−2

differ)

erg

3×10

statcoulomb

3×10

statvolt . (1.9)

In Gaussian units, the unit of magnetic ﬁeld, namely the

Gauss (B)orOersted(H ) has the same physical size

and dimension as the unit of electric ﬁeld, namely the

statvolt/cm, which in turn corresponds to an SI ﬁeld

3×10

V/m. However, the tesla (1 T = 1 weber/m

the SI unit of magnetic ﬁeld B (older texts refer to B as

the magnetic induction), has the physical dimensions of

Vs/m

. To ﬁnd the correspondence to Gaussian units,

one must multiply by the speed of light c:

1Tc =

3×10

V/m , (1.10)

which corresponds to 10

statvolt/cm and hence to

gauss.

Tables 1.3 and 1.4 related basic mechanical and

electromagnetic quantities in the different unit sys-

tems. Caution is required both because the same

symbol often stands for quantities of different phys-

ical dimensions in different systems of units, and

because factors of 2 π sometimes enter frequencies,

depending on whether the units are cycles/s (Hz)

or radians/s. The double-headed arrows (↔) indicate

a correspondence between quantities whose dimen-

sions are not necessarily equal. Thus for example, the

force on an electron due to a Gaussian electric ﬁeld

of 1 statvolt/cm is the same as due to an SI elec-

tric ﬁeld of

3×10

V/m. The correspondences between

Gaussian and SI electrostatic quantities become equal-

ities if and only if 4π

= 1. Thus they are equalities

within the Gaussian system but not within the less

constrained SI scheme. The SI and Gaussian units of

magnetic ﬁeld have different dimensions unless both



and c are set equal to dimensionless numbers.

Natural H–L units can be considered SI units sup-

plemented by the conditions 

= c = = 1. They are

listed here in units of meters, although eV are also of-

ten used: 1 eV = 5.067 731 04(43) ×10

−1

× c.The

correspondences may be considered equalities within

the natural H–L system but not within SI. Note that

the electronic charge in the natural H–L system has

the magnitude e =

√

4πα. More electromagnetic con-

versions can be found in Jackson [1.2]. The data

here are based on the 2002 adjustment by Mohr and

Taylor [1.1].

A few additional energy conversion factors are

1eV= 1.602 176 53 (14) ×10

−19

= 2.417 989 40 (21) ×10

Hz × h

= 8065.544 45 (69) cm

−1

× hc

= 3.674 932 45 (31) ×10

−2

= 1.160 4505 (20) ×10

K×k

= 96.485 3383 (83) kJ mol

−1

The basic unit of temperature, the kelvin, is equiva-

lent to about 0.7cm

−1

, i. e., the value of the Boltzmann

constant k

expressed in wavenumber units per kelvin is

0.695 0356(12) cm

−1

. Since K is the internationally

accepted symbol for the Kelvin [1.3], this suggests that

the use of the letter K as a symbol for 1 cm

−1

(1 Kayser)

should be discontinued.

Introduction

Units and Constants 1.3 Mathematical Constants 5

1.2 Atomic Units

Atomic and molecular calculations based on the

Schrödinger equation are most conveniently done in

atomic units (a.u.), and then the ﬁnal result converted to

the correct SI units as listed in Table 1.4. In atomic units,

= m

= e = 4π

= 1. The atomic units of length,

velocity, time, and energy are then

length: a

4π

αm

velocity: v

4π

= αc ,

time: τ

16π



energy: E

4π

= α

where, from the deﬁnition (1.8), the numerical value

of c is α

−1

= 137.035 999 11(46) a.u. For the lowest

1s state of hydrogen (with inﬁnite nuclear mass), a

the Bohr radius, v

is the Bohr velocity, 2πτ

is the

time to complete a Bohr orbit, and E

(the Hartree

energy) is twice the ionization energy. To include the

effects of a ﬁnite nuclear mass M, one must replace

the electron mass m

by the reduced electron mass

µ = m

M/(M +m

Atomic energies are often expressed in units of the

Rydberg (Ry). The Rydberg for an atom having nuclear

mass M is

1Ry= R

∞

= M(M +m

)

−1

∞

(1.11)

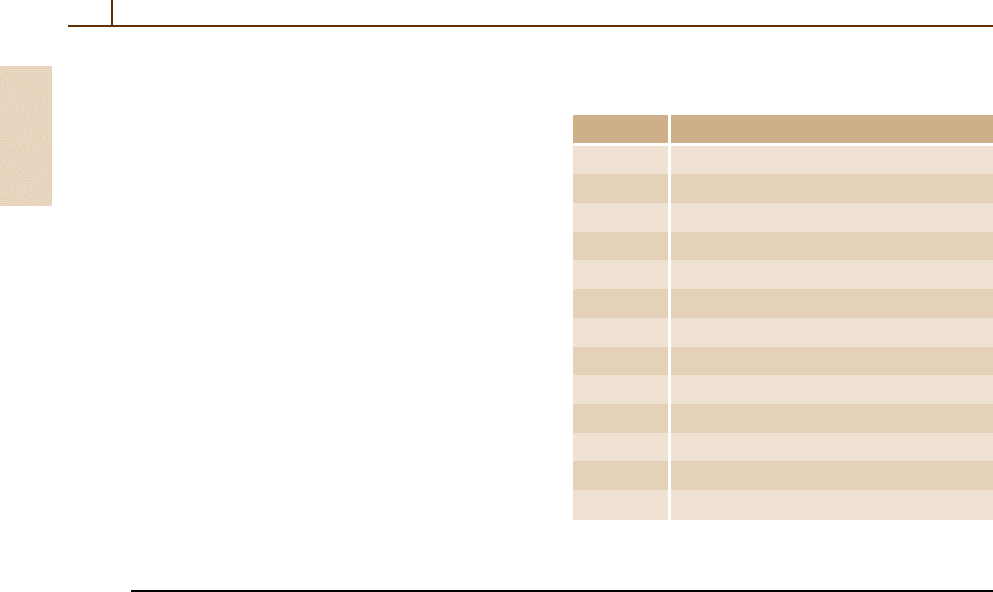
Table 1.4 Physical quantities in atomic units with = e =

= 4π

= 1, and α

−1

= 137.035 999 11(46)

Quantity Unit Value

Length a

0.529 177 2108(18) × 10

−10

Mass m

0.910 938 26(16) × 10

−30

Time /E

2.418 884 326 505(16) × 10

−17

Velocity v

≡ αc 2.187 691 2633(73) × 10

−1

Energy E

4.359 744 17(75) × 10

−18

Action 1.054 571 68(18) × 10

−34

Force E

0.823 872 25(14) × 10

−7

Power E

/ 0.180 237 811(31) W

Intensity E

/ a

64.364 091(11) × 10

−2

Charge e 1.602 176 53(14) × 10

−19

Electric E

/e 27.211 3845(23) V

potential

Electric E

/ea

= 0.514 220 642(44) × 10

−1

ﬁeld α c/ea

Magnetic E

/ea

αc 2.350 517 42(20) × 10

ﬂux density

with

∞

cα

= 10 973 731.568 525 (73) m

−1

(1.12)

The Rydberg constant R

∞

is thus the limiting value of

for inﬁnite nuclear mass, and hcR

∞

a.u., which

is equivalent to 13.605 6923(12) eV.

The energy equivalent of the electron mass, m

is 0.510 998 918(44) MeV. This energy is a natural unit

for relativistic atomic theory. For example, for inner-

shell energies in the heaviest elements, the binding

energy of the 1s electron in hydrogenic Lr (Z = 103)

is 0.338 42 m

1.3 Mathematical Constants

A selection of the most important mathematical con-

stants is listed in Table 1.5. More extensive tabulations

and formulas can be found in the standard mathematical

works [1.4, 5]

1.3.1 Series Summation Formula

The Riemann zeta function deﬁned by ζ(n) =



∞

i=1

−n

(Table 1.5) is particularly useful in summing slowly

convergent series of the form

S =

∞



i=1

. (1.13)

For example, suppose that the series

= t

−2

−3

+··· (1.14)

for the individual terms in S is rapidly convergent

for i > N,whereN is some suitably large integer.

Introduction

6 Part

Then

S =



i=1

(2) +t

(3) +···, (1.15)

where ζ

(n) = ζ(n) −



i=1

−n

is the zeta function

with the ﬁrst N terms subtracted. For N sufﬁciently

large, only the ﬁrst fe w t

coefﬁcients need be known,

and they can be adequately estimated by solving the

system of equations

= t

−2

−3

+···

k+2

−k−2

, (1.16a)

N−1

= t

(N −1)

−2

(N −1)

−3

+···

k+2

(N −1)

−k−2

, (1.16b)

N−k

= t

(N −k)

−2

(N −k)

−3

+···

k+2

(N −k)

−k−2

, (1.16c)

where k +1 ≤ N is the number of terms retained in

(1.14).

Table 1.5 Values o f e, π, Euler’s constant γ , and the Rie-

mann zeta function ζ(n)

Constant Value

e 2.718 281 828 459 045 235 360 287 471 352 66

π 3.141 592 653 589 793 238 462 643 383 279 50

1/2

1.772 453 850 905 516 027 298 167 483 341 14

γ 0.577 215 664 901 532 860 606 512 090 082 40

ζ(2) 1.644 934 066 848 226 436 472 415 166 646 02

ζ(3) 1.202 056 903 159 594 285 399 738 161 511 45

ζ(4) 1.082 323 233 711 138 191 516 003 696 541 16

ζ(5) 1.036 927 755 143 369 926 331 365 486 457 03

ζ(6) 1.017 343 061 984 449 139 714 517 929 790 92

ζ(7) 1.008 349 277 381 922 826 839 797 549 849 80

ζ(8) 1.004 077 356 197 944 339 378 685 238 508 65

ζ(9) 1.002 008 392 826 082 214 417 852 769 232 41

ζ(10) 1.000 994 575 127 818 085 337 145 958 900 31

References

1.1 P. J. Mohr, B. N. Taylor: Rev. Mod. Phys. 77,

1 (2005); see also www.physicstoday.org/guide/

fundcon.html; all of the values, as well as the cor-

relation coefﬁcients between any two constants, are

available online in a searchable database provided

by NIST’s fundamental constants data center. The

internet address is http://physics.nist.gov/constants

1.2 J. D. Jackson: Classical Electrodynamics, 3rd edn.

(Wiley, New York 1999)

1.3 B. N. Taylor (Ed.): The International System of Units

(SI), NIST Spec. Publ. 330 (U.S. Government Printing

Ofﬁce, Washington 2001) p. 7

1.4 M. Abramowitz, I. A. Stegun: Handbook of

Mathematical Functions (Dover, New York

1965)

1.5 I. S. Gradshteyn, I. M. Ryzhik: Table of Inte-

grals, Series, and Products (Academic, New York

1965)

Introduction