Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing

Подождите немного. Документ загружается.

248 Part B Chemical and Microstructural Analysis

spin

γ-rays

Counter

Time

W(θ)=1+Acos(θ)

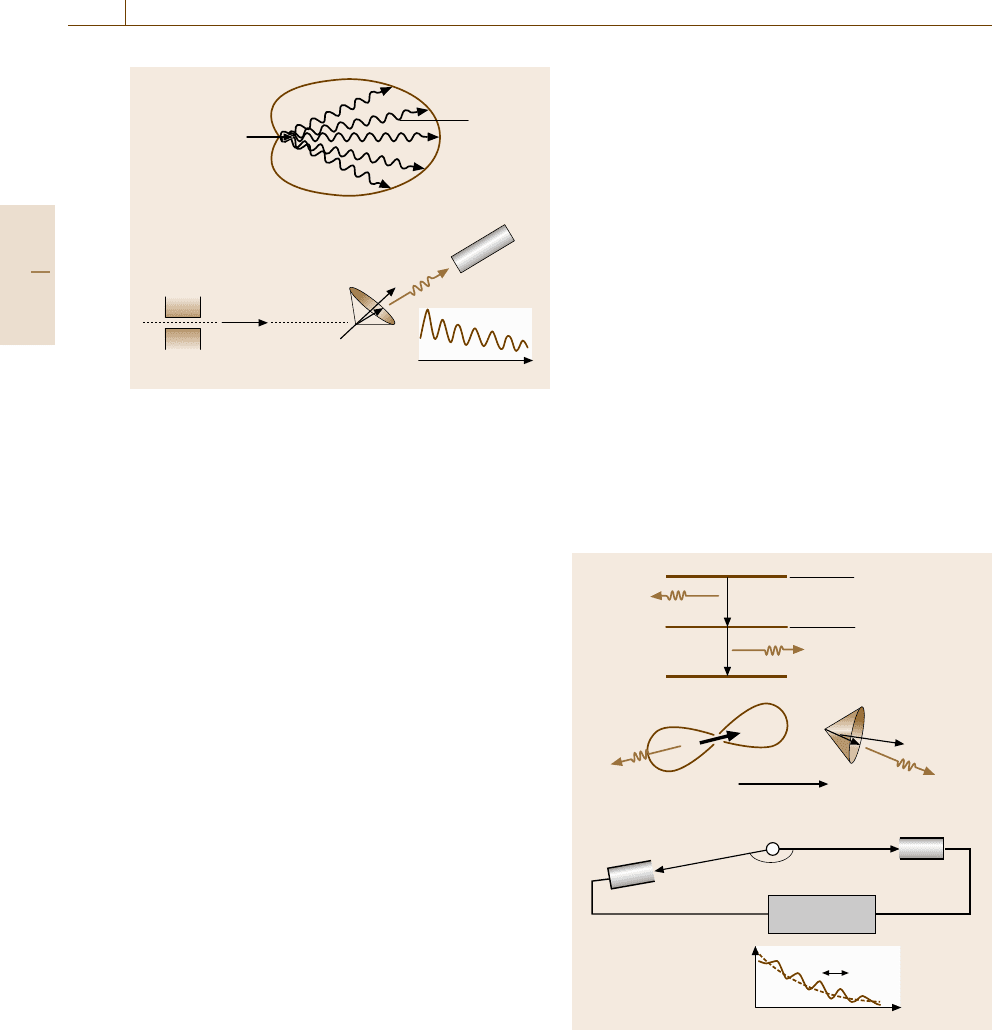
Fig. 5.60 (a) Directional emission of γ -rays from μ

spin

and (b) a setup of μ

SR experiments

lifetime. This provides a means to detect the diffusion

of vacancies introduced by irradiation with high en-

ergy particles [5.53]. At low temperatures, the diffusion

of μ

along interstitial sites is so slow that they ex-

hibits a characteristic rotation frequency corresponding

to the internal magnetic ﬁeld at the interstitial site. As

the temperature increases, however, μ

become mobile,

and once trapped by a vacancy, show a different rota-

tion frequency. At temperatures where the vacancies are

annihilated, the signal then disappears again. Thus, de-

tecting the change of the μ

SR signal with temperature,

one could study the recovery process of point defects.

Perturbed Angular Correlation (PAC). Some radioac-

tive nuclei such as

111

Ag and

111

In emit two γ -rays

(or particles) successively in the nuclear transformation

process (Fig. 5.61a). If the lifetime of the intermediate

state is short (< hundreds ns), there exists an angu-

lar correlation between the two rays. In the absence of

external ﬁelds such as a magnetic ﬁeld and an elec-

tric ﬁeld gradient, the direction of the second γ -ray

is oriented principally in the direction of the nuclear

spin at the time of the ﬁrst γ -ray emission. As illus-

trated in Fig. 5.61b, when an external ﬁeld is present as

a perturbation and if the intermediate nuclei have a mag-

netic moment, the spins rotate during the intermediate

lifetime. This is detected as a signal oscillating at the

Larmor frequency by a counter for the second γ -rays

emitted in coincidence with the ﬁrst ones (Fig. 5.61c).

This perturbed angular correlation (PAC) method allows

one to study the recovery process of point defects in

a manner similar to μ

SR.

Solid-State NMR. A famous example of applications

of NMR spectroscopy to solids is the measurement of

the diffusion rate of atoms. Nuclei feel a local magnetic

ﬁeld of various origins (Sect. 5.4.2) other than a large

external magnetic ﬁeld. The ﬂuctuations of the local

magnetic ﬁeld due to the motion of nuclei in solids gives

rise to lateral alternating ﬁelds with a frequency compo-

nent that causes resonant transitions between Zeeman

levels. This ﬂuctuation-induced transition results in an

energy relaxation of the spin system and shortening of

the spin–lattice relaxation time T

. The reduction of

occurs most efﬁciently when the correlation time of

ﬂuctuations τ satisﬁes ω

τ ≈1, where ω

denotes the

Larmor frequency. The ﬂuctuation time constant τ rep-

resents the time constant of atomic jumps and therefore

depends on temperature if the atomic jumps are ther-

mally activated. So, if one measures T

as a function

of temperature, one ﬁnds that T

becomes minimum

at a certain temperature Θ

min

.Sinceω

can be varied

by changing the external magnetic ﬁeld, the activation

energy and the frequency prefactor of atomic jumps

–t/τ

Lifetime τ

Coincidence

count circuit

Excited state

Intermediate state

(lifetime τ)

Fig. 5.61a–c In perturbed angular correlation (PAC)ex-

periments, each direction of two γ -rays successively

emitted (a) indicates the direction of the intermediate nu-

clear spin, which may rotate under an internal magnetic

ﬁeld (b). The spin rotation during the lifetime is detected

by coincident count electronics

(c)

Part B 5.3

Nanoscopic Architecture and Microstructure 5.3 Lattice Defects and Impurities Analysis 249

could be evaluated from an Arrhenius plot of ω

(=τ

−1

)

versus Θ

min

obtained for various magnetic ﬁelds. In

ordinary measurements, however, the jump rate τ

−1

is limited to the narrow range of Larmor frequencies

≈ 10

–10

−1

. Experimentally this range can be

expanded down to 1 s

−1

by employing the rotating ﬁeld

method [5.54] in which the effective ﬁeld is given by

a rotating magnetic ﬁeld with a small amplitude which

is resonant with the Larmor frequency. The range of

the jump rate τ

−1

covered by such NMR measurements

may be further reduced to 10

−3

–10

−2

−1

in ionic crys-

tals due to the absence of the free electrons that would

induce additional relaxation in metals limiting the cor-

rect measurement of T

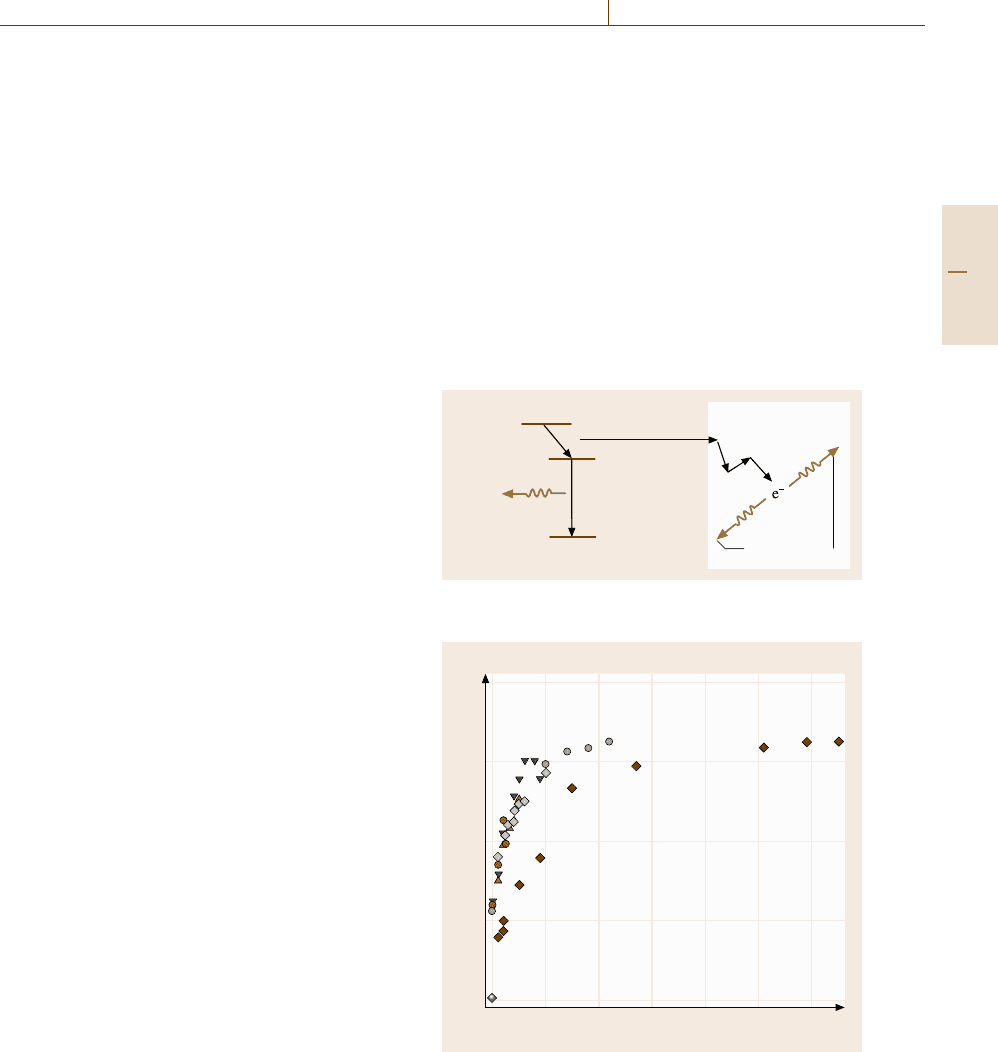
Positron Annihilation Spectroscopy (PAS). The posi-

tron is the antiparticle of the electron with the same

mass as the electron but an electric charge of +e [5.61,

62]. Positrons are created as a decay product of some

radioactive isotopes such as

Na,

Co and

Cu. For

the case of the parent nucleus being

Na shown in

Fig. 5.62, a positron e

is emitted from the source with

an energy of hundreds of keV on the β

decay of the

Na to an intermediate nucleus of

∗

(

∗

indicates

that the nucleus is in an excited state). The unstable

∗

immediately, within 0.3 ps, relaxes to the sta-

ble

Ne by emitting a γ -ray of 1.28 MeV in energy.

The generated positron, if injected into a solid, loses

its energy rapidly within ≈ 1 ps by inelastic collision

with the lattice (thermalization), and after some du-

ration (100–500 ps) is annihilated with an electron in

the solid. On this positron annihilation, two γ -rays of

0.511 MeV are emitted in almost opposite directions.

Among various schemes of positron annihilation

spectroscopy (PAS), the simplest is the positron lifetime

measurement. The lifetime can be measured as the time

difference between the emission of the 1.28 MeV γ-ray,

that indicates the time of the introduction of a ther-

malized positron into the sample, and the emission of

the 0.511 MeV γ -rays that indicates the occurrence of

an annihilation event. The positron lifetime reﬂects the

density of the electrons with which they are annihilated.

Since e

is positively charged, if the crystalline sample

contains no imperfections, they migrate along intersti-

tial sites until they are annihilated with electrons along

the diffusion path. However, if the crystal contains va-

cant defects (vacancies, microvoids, dislocation cores

etc.), the positrons are trapped by them because the

missing ions form an attractive potential for positrons.

Once the positron is trapped at a vacant site, it has less

chance of being annihilated with an electron and as a re-

sult the lifetime is elongated signiﬁcantly. Figure 5.63

shows the positron lifetime calculated for multiple va-

cancies of various sizes. From comparison of the exper-

imental value of positron lifetime with the theoretical

predictions, one can reliably infer the number of vacan-

cies if it is smaller than ≈10. When vacancies of differ-

ent sizes coexist in the sample, the positron lifetime has

a spectrum consisting of components each representing

one type of vacancies of a different size. A successful

example of positron lifetime spectroscopy is its applica-

tion to measurements of thermal vacancy concentration

as a function of temperature [5.63]. When the sample

contains only monovacancies, the component with long

lifetime increases proportionally with the increasing va-

Hundreds keV

0.3 ps

1.28 MeV γ

0.511 MeV γ

Thermalized

within–1ps

Fig. 5.62 Generation of a positron and its annihilation with

an electron in solids

Positron lifetime (ps)

500

400

300

200

100

20 60

Number of vacancies

504030100

Fig. 5.63 Calculated positron lifetime for vacancies of var-

ious sizes. Experimental data for Si are collected from

literature [5.55–57]. Theoretical values for vacancies in Si

calculated [5.58,59] are indicated with open marks. Experi-

mental data for Fe [5.60] are also shown (solid diamonds)

for comparison. Courtesy of Prof. M. Hasegawa

Part B 5.3

250 Part B Chemical and Microstructural Analysis

cancy concentration, as long as the vacancies are not

saturated with positrons. Owing to the preferential trap-

ping of positrons to vacancies, the detection limit of

vacancy concentrations is enhanced by 2–3 orders of

magnitude compared to the dilatometric method [5.64].

Since PAS experiments can be conducted irrespective

of sample temperature, the vacancy concentration can

be measured in thermal equilibrium, which is an advan-

tage over the resistometric techniques that need sample

quenching from various annealing temperatures.

The directions of the two γ -rays emitted on positron

annihilation are not completely opposite due to the fact

that the electrons to be annihilated have a ﬁnite momen-

tum whereas the momentum of thermalized positrons

is negligible: the larger the electron momentum, the

larger the correlation angle (Similarly, the energy of

γ -rays emitted on positron annihilation reﬂects the ki-

netic energy of the electrons through a Doppler effect.

The Doppler shift measurements provide information

similar to that given by the γ –γ angular correla-

tion. The coincident Doppler broadening technique is

found to be useful for the identiﬁcation of impurities

bound to vacancy defects [5.65].). Figure 5.64 illus-

trates a schematic γ –γ angular correlation curve which

consists of a parabolic component, which arises from

annihilation with conduction electrons whose momen-

tum is relatively small, and a Gaussian component,

which is due to annihilation with core electrons whose

momentum extends to larger values. The potential felt

by conduction electrons at vacancy sites is shallower

and the electron momentum is smaller than the perfect

sites. So, if the positrons are trapped by vacancy-

type defects, the parabolic component becomes sharper

and increases its intensity at the expense of the core

Coincident counts

k ≈ electron momentum

Gaussian

Core electrons

Parabolic

Conduction electrons

0 θ

Fig. 5.64 Setup of γ –γ angular correlation experiments

and a schematic correlation spectrum

component. Various line shape parameters have been

proposed to quantify this curve shape change and used

to investigate, for example, the agglomeration of va-

cancies in electron-irradiated crystal upon isochronal

annealing [5.66]. Nowadays, γ –γ angular correlation

experiments are conducted in two-dimensions by us-

ing two position-sensitive detectors in a coincidence

arrangement. The 2-D-angular correlation of annihila-

tion radiation (2-D-ACAR) is a modern method that

allows one to investigate nanosize crystalline phases

such as G-P zones enriched with transition metals in

noble metals such as Cu and Ag [5.67].

The detection limit of vacancies by PAS is usually

around 10

−6

in metals. In semiconducting materials,

it may be enhanced by two orders of magnitude at

low temperatures when the vacancies are negatively

charged. Since the positrons initially emitted from the

positron source (e.g.,

Na) have an energy of the or-

der of hundreds of keV, they can penetrate deep into the

sample (≈1mminSi,≈0.2 mm in Fe), so the thickness

of the samples must be of the order of 1 mm. The use

of slow positron beams, with energy ranging between

a few eV and several tens of keV, enables one to study

the depth proﬁle of point defects, a problem of particu-

lar importance in semiconductor device technology.

Mößbauer Spectroscopy. The Mößbauer spectroscopy

is based on the recoil-less radiation and absorption of

γ -rays by Mößbauer nuclei embedded in solids with an

extremely narrow natural width (≈ 5×10

−9

eV) . S em i-

classically, the conservation of the momentum and the

energy of the emitted (or absorbed) γ -ray and the solid

suspending the nucleus requires that a part of the γ -ray

energy

2Mc

(5.34)

must be transferred to the nucleus as a recoil energy.

Here E

is the energy of the γ -ray, M the nuclear mass,

and c the light velocity. Quantum mechanically, how-

ever, the motion of nuclei is quantized in the form of

phonons, so if E

< Ω (phonon energy), the emis-

sion and absorption of γ -rays occurs free of recoil.

The condition for this recoil-less radiation and absorp-

tion is k

> E

/Mc

, where k

is the Boltzmann

constant, and θ

the Debye temperature of the crystal.

The most common combination of an emitter and an

absorber satisfying this condition is

Co (half life =

270 d) and

Fe (natural abundance = 2.17%) between

which 14.413 keV γ -rays are transferred.

Part B 5.3

Nanoscopic Architecture and Microstructure 5.3 Lattice Defects and Impurities Analysis 251

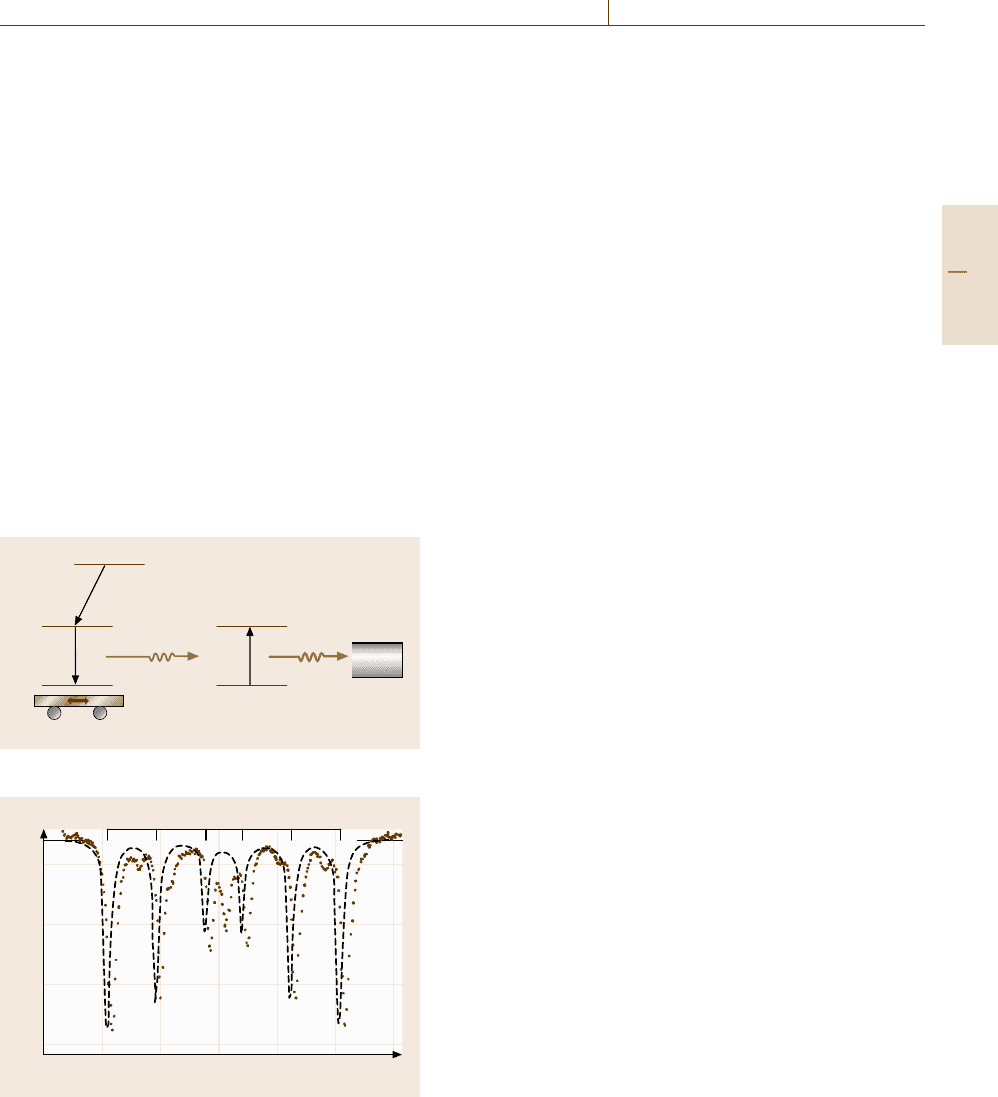
Figure 5.65 shows a typical setup for Mößbauer ex-

periments. The γ -ray source (e.g.,

Co) is mounted

on a stage that can be moved with various velocities

(0 to ± several mm/s) so as to change the γ-ray energy

by the Doppler effect. A sample containing the γ -ray

absorber (

Fe for

Co source) is irradiated with the

γ -rays and the absorbance is measured by a γ -ray de-

tector as a function of the Doppler-shifted γ-ray energy.

Although the experiments are applicable only to lim-

ited stable isotopes (

Fe,

Ni,

Zn,

Ge,

119

Sn,

121

Sb,

184

W) Mößbauer spectroscopy places no severe

restrictions on the temperature and the environment of

the samples, other than that the sample thickness should

be in the range 2–50 μm depending on the concentra-

tion of the absorber.

The degeneracy of the states of a nucleus in a solid is

lifted under the inﬂuence of the local environment. For

absorber nuclei having a nuclear spin, the internal mag-

netic ﬁeld, if present, can be evaluated by measuring the

nuclear Zeeman splitting, which is more than one order

270 d

γ-rays

Doppler

shifted

Source

Absorber Detector

Fig. 5.65 Experimental setup for Mößbauer spectroscopy

2.00

1.95

1.90

1.85

×10

100

150

200 250 300 350

Counts

Channel number

Fig. 5.66 Mößbauer spectra of iron-4.2% carbon marten-

site (dots A) and of pure α-iron (broken line B). The central

peak is due to the presence of paramagnetic austenite phase

(after [5.68])

of magnitude larger than the natural width of the γ -rays.

This provides a good probe of ferromagnetic phases,

which is demonstrated for the case of quenched iron

steel ([5.68]) in Fig. 5.66. For absorber nuclei having

a quadrupole moment (I > 1/2), the Mößbauer spec-

troscopy allows one to assess the electric ﬁeld gradient

at the nuclei by measuring the quadrupole splitting. This

can be applied to the detection of symmetry breaking

of crystal ﬁeld by the presence of point defects in the

vicinity of the absorber nuclei. Since the thermal mo-

tion of absorber nuclei causes a Doppler shift, a careful

analysis of the spectral line shape gives us information

on the lattice vibrations that may be affected by lattice

defects.

Deep-Level Transient Spectroscopy (DLTS). Point de-

fects in semiconductors often form deep levels in the

band gap. Deep-level transient spectroscopy (DLTS)

allows quantitative measurements of the density and

the position of the gap levels with respect to the rele-

vant band edge. The charge state of deep-level centers

can be changed by various means such as impurity

doping, electronic excitations, and carrier injection.

The thermal occupation of a deep level, once dis-

turbed by some means, is recovered by a thermally

activated release of the carriers trapped at the centers

by the disturbance. The recovery rate is determined

by the depth of the electronic level from the rele-

vant band edge (the conduction band edge for electron

traps or the valence band edge for hole traps). In stan-

dard DLTS experiments, the objects to be measured

are deep-level centers located in the depletion layer

beneath a metal–semiconductor contact fabricated on

the sample surface. The change of the electronic oc-

cupancy of the centers is detected by the change of

the electrostatic capacitance associated with the con-

tact, and the electronic disturbance is caused by carrier

injection through the contact or photocarrier gener-

ation. From the temperature dependence of the rate

of capacitance recovery, we can evaluate the energy

depth of the gap level, and from the amount of re-

covery, we can measure the density of the center. An

advantage of DLTS over optical spectroscopic meth-

ods is that, from the sign of the capacitance change,

we can determine which carriers (electrons or holes)

are transferred between the gap level and the related

band, and therefore can deﬁnitely know from which

band edge the level depth is measured. The capacitance

spectroscopic methods including DLTS haveasensi-

tivity as high as ≈ 10

−3

in moderately doped

samples.

Part B 5.3

252 Part B Chemical and Microstructural Analysis

5.3.2 Extended Defects

For extended defects, most diffraction methods are

coupled with microscopic methods based on crystal

diffraction. Also, spectroscopic methods are not speciﬁc

to extended defects, other than that the number of the

centers in extended defects to be studied is generally too

small unless the sample is prepared by intentionally in-

troducing the defects at a high density. The description

in this subsection, therefore, is limited to microscopic

methods.

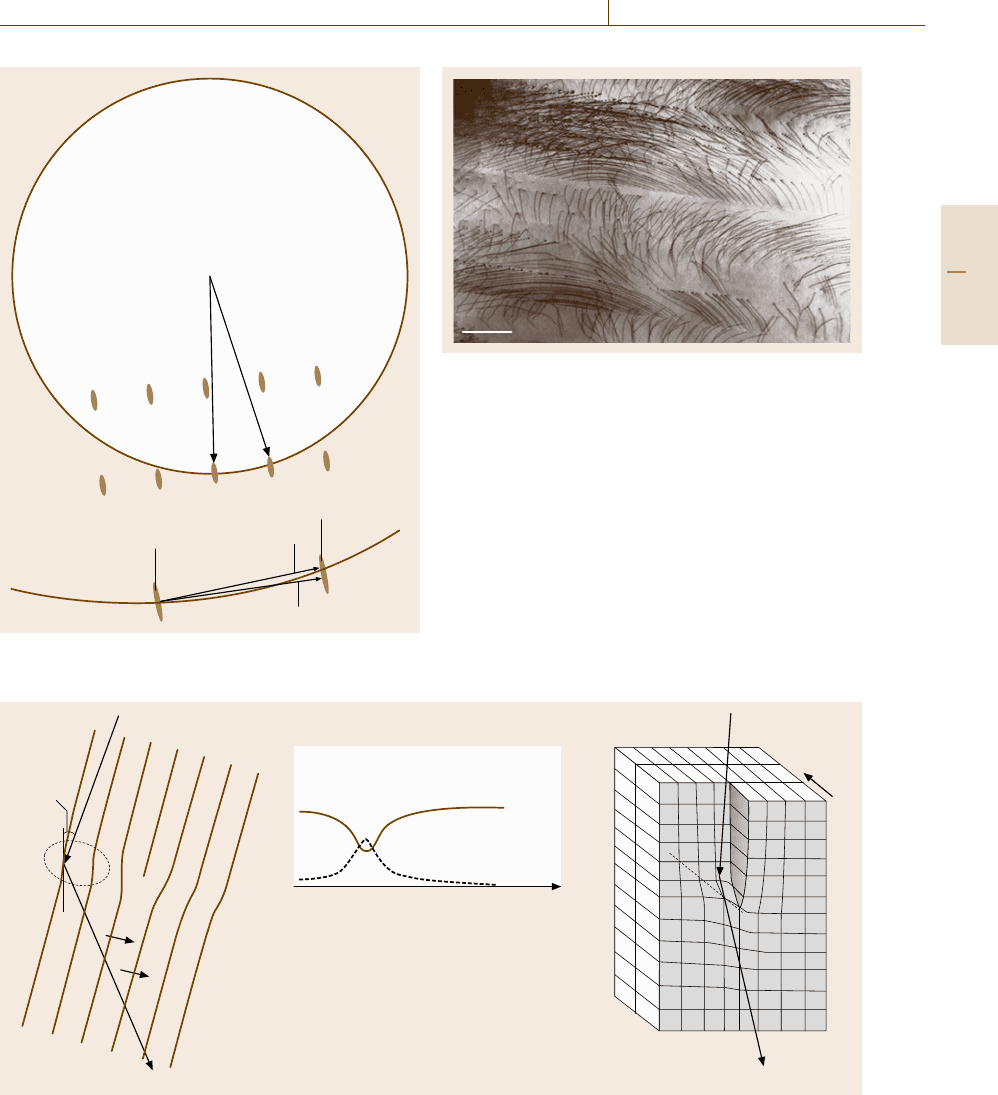
Chemical Etching

A simple method for direct observation of extended

defects is chemically etching the sample surface to re-

veal the defects as etch pits, hillocks, and grooves that

develop according to the difference in the chemical re-

activity at the defect sites. Figure 5.67 demonstrates an

example of such etching patterns observed by optical

microscopy on a chemically etched surface of a plasti-

cally deformed CdTe crystal. The left diagram shows

the traces of the pits positions tracked by successive

removal of the surface. The linear nature of the traces

proves that these defects are dislocations. The chemical

etching method is also applicable to planar defects, such

as grain boundaries and stacking faults that intersect the

surface. The resolution may be enhanced by the use of

Surface

Depth Position of etch pits

B5 μm

5 μm

Fig. 5.67 Optical microscopic images of dislocation etch pits revealed on a plastically deformed CdTe surface by wet

chemical etching (after [5.69])

SEM-SE if etching is stopped before etching patterns

overlap.

Transmission Electron Microscopy (TEM)

Dislocations. Among extended defects, dislocations are

the most common objects, for which TEM displays

its full capability. A standard scheme for observations

of dislocations is to employ a two-beam condition in

which the sample crystal is tilted in such orientations

that only one diffraction g is strongly excited, as shown

schematically in Fig. 5.68. For plan-view imaging an

edge dislocation lying nearly in parallel to the sample

surface (Fig. 5.69a), we tilt the sample to the direc-

tion parallel to the Burgers vector b so as to bring the

sample to a two-beam condition. Then, we tilt the sam-

ple slightly further away from the Bragg condition, so

that we allow lattice planes only near the dislocation

to satisfy the Bragg condition. In this conﬁguration,

the primary (direct) beam is diffracted strongly near

the dislocation, and as a result, if we are looking at

the bright ﬁeld image, the dislocations are observed as

dark lines as shown in Fig. 5.70. For screw dislocations

(Fig. 5.69c), since the lattice planes normal to the dislo-

cation line and hence the Burgers vector b are inclined

near the core, the plan-view dislocation contrast arises

from the same mechanism. Thus, regardless of whether

dislocations are of edge or screw type, the dislocation

Part B 5.3

Nanoscopic Architecture and Microstructure 5.3 Lattice Defects and Impurities Analysis 253

k–k

≡ K = g + s

Fig. 5.68 Two-beam diffraction condition; s denotes the

deviation from the Bragg condition

BF contrast

a) b) c)

DF contrast

Dislocation position

Fig. 5.69a–c Imaging dislocations (a) edge, (c) screw under two-beam conditions. The diffraction is locally enhanced at

a position near the dislocation core where the lattice planes are tilted so that the Bragg condition is locally satisﬁed. The

Burgers vector can be determined by the invisibility criterion (g ·b) =0

0.2 µm

Fig. 5.70 TEM image of dislocations in plastically de-

formed 6H-SiC

contrasts are obtained when (g ·b) = 0. In other words,

when

(g ·b) =0 (5.35)

the dislocation contrasts diminish, as demonstrated in

Fig. 5.71. More precisely, dislocations are not neces-

sarily invisible even if (g ·b) =0when(g ·b × u) =0,

where u denotes the unit vector parallel to the dis-

location line. Examining this invisibility criterion for

various g vectors, one can determine the direction of

the Burgers vector. It should be noted that, for determi-

Part B 5.3

254 Part B Chemical and Microstructural Analysis

1 μm

Fig. 5.71 TEM images of dislocation lines in Mo acquired for two

different diffraction conditions. The invisibility criterion is used to

determine the Burgers vector (after [5.70])

nation of the sense and the magnitude of the Burgers

vector, we need some additional information [5.14].

When the dislocations are dissociated into partial

dislocations separated by a narrow stacking fault, imag-

ing in the normal two-beam condition is enough neither

to resolve each partial dislocation nor give the correct

position of the cores. In such cases, the weak-beam

dark-ﬁeld method is useful for imaging dislocation lines

with a width of ≈ 1.5 nm and a positional deviation of

only ≈ 1 nm from the real core. Figure 5.72 demon-

strates a weak-beam image of dissociated dislocations

in a CoSi

single crystal.

000

0.1 μm

440

220

Fig. 5.72 A weak-beam TEM image of dissociated dislocations in CoSi

(Courtesy of M. Ichihara)

High-resolution transmission electron microscopy

(HRTEM) is applicable to imaging edge disloca-

tions. As explained in Sect. 5.1.2, under an appropriate

(Scherzer) defocus condition, HRTEM images approx-

imately represent the arrangement of atomic rows

viewed along the beam direction. Figure 5.73ashows

an HRTEM lattice image of an end-on edge disloca-

tion penetrating a ZnO sample ﬁlm. The presence of

the dislocation can be recognized by tracing a Burgers

circuit drawn around the dislocation core. One should

note that the HRTEM is not applicable to imaging screw

dislocations, because screw dislocations would not be

visible as such a topological defect in the end-on conﬁg-

uration. A modern HRTEM technique has been shown

to be able to visualize the strain ﬁeld around a single

dislocation [5.71].

Planar Defects. There are many types of planar de-

fects, stacking faults, antiphase boundaries, inversion

domain boundaries, twin boundaries, grain boundaries,

and phase boundaries, each of which is characterized

by a translation vector R, a crystal rotation, lattice mis-

ﬁt and so on by which the crystal on one side of the

boundaries is displaced relative to the other. In this sub-

section, we conﬁne ourselves mainly to stacking faults

(SFs), representative planar defects in crystals, which

are characterized by only a constant translation vec-

tor R.

As mentioned in Sect. 5.1.2, the dynamical theory

in perfect crystals under two-beam conditions may be

extended to imperfect crystals by introducing an addi-

Part B 5.3

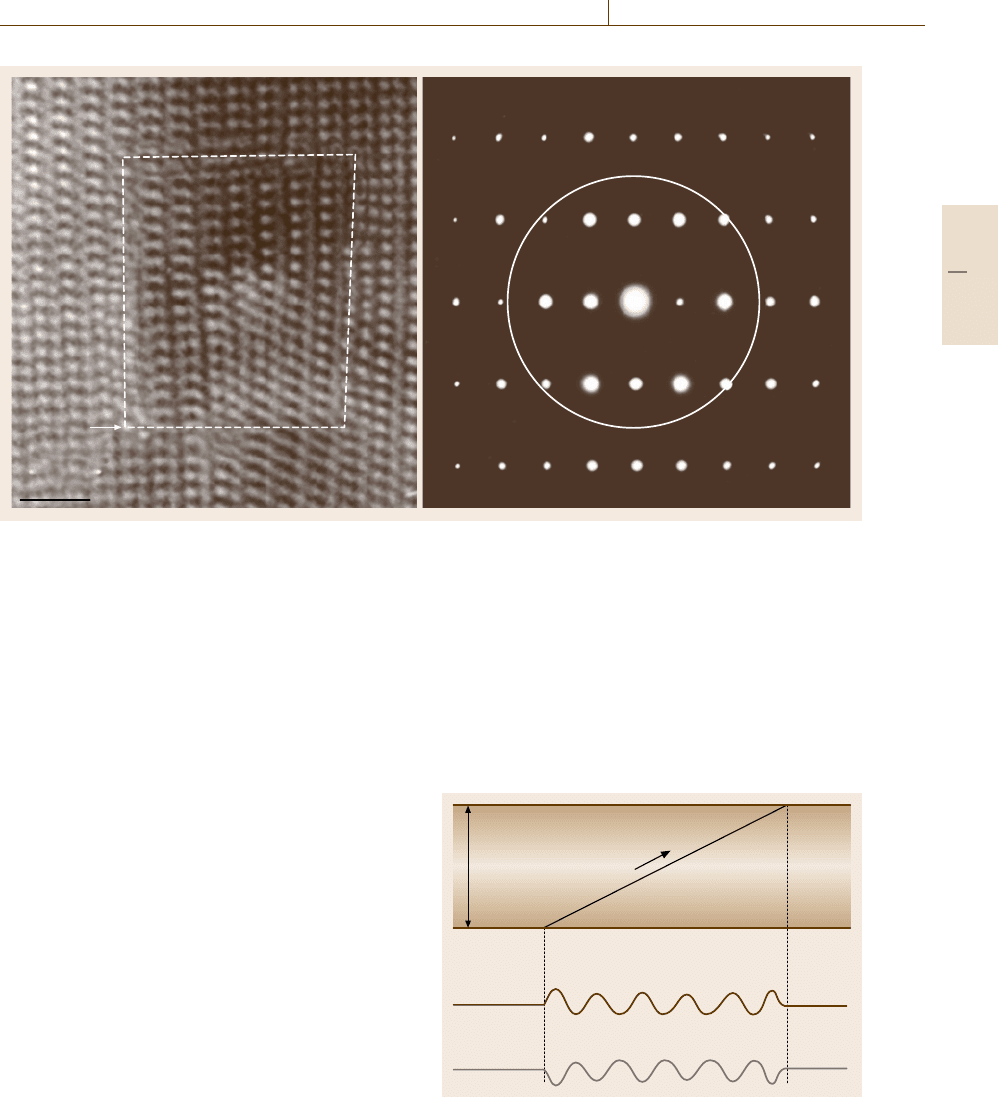
Nanoscopic Architecture and Microstructure 5.3 Lattice Defects and Impurities Analysis 255

1 nm

Fig. 5.73 (a) HREM image of an edge dislocation in ZnO (b) the diffraction spots encircled were used for HREM imaging

(Courtesy of M. Ichihara)

tional phase shift

α =2πg · R (5.36)

into the arguments. Here R(r) is the displacement of

atoms from the perfect positions r due to the pres-

ence of the defects. Therefore, quite generally, if α =0,

there arises no TEM contrast of the defects. Also as

mentioned in Sect. 5.1.2, the Pendellösung effect is

a consequence of beating between the two Bloch waves

excited on the two dispersion branches. Arriving at

a planar defect, the two Bloch waves each generates two

other Bloch waves with a phase shift interfering with

the other. A detailed analysis (see for example [5.15,

p. 381]) shows that fringe contrasts as illustrated in

Fig. 5.74 should be observed by TEM with a period

that is half of the thickness (Pendellösung) fringe ex-

pected for a wedge-shaped sample of the upper part of

the crystal above the SF plane.

Stacking faults are grouped into two types, intrin-

sic SFs, which are formed by interplanar slips of lattice

planes with a translation vector (= lattice periodicity)

parallel to the SF planes or by coalescence of vacancies

with a translation vector normal to the SF planes, and

extrinsic stacking faults, which are formed by coales-

cence of self-interstitial atoms with a translation vector

normal to the SF planes. All types of SFs, if closed in

a crystal, are bounded by a loop of partial dislocation.

In fcc crystals, the so-called sessile (unable to glide)

Frank partial dislocations bounding the vacancy-type

and the interstitial-type SFs have Burgers vectors R of

±1/3[111]equal in magnitude but opposite in direction,

while the so-called glissile Shockley partial dislocations

bounding the other type of intrinsic SFs have a Burg-

ers vector R of 1/6[11

2]. The invisibility criterion is,

therefore, different for the Shockley-bounded SFs and

Stacking

fault

Sample

film

Fig. 5.74 TEM fringe contrasts of a stacking fault when

absorption is neglected. The period is half that expected

from the thickness fringe. The contrast is reversed in x-ray

topography

Part B 5.3

256 Part B Chemical and Microstructural Analysis

b =R

b = R

b =R

Inside

contrast

Outside

contrast

Ewald sphere

Fig. 5.75 Inside–outside contrast method for distinguish-

ing interstitial- (upper) and vacancy-type (lower) stacking

faults

0.5 μm

Fig. 5.76 TEM image of intrinsic stacking faults bounded by

Shockley partial dislocations (PD

and PD

). The sample is a plas-

tically deformed 6H-SiC single crystal

the others. To determine experimentally whether the

SFs are interstitial loops or vacancy loops and the

sense of inclination of SF planes in the sample, the

inside–outside contrast method illustrated in Fig.5.75

is used [5.15, p. 410]. The same method is also useful

for determining the sense of the Burgers vectors of gen-

eral dislocations. Figure 5.76 shows a TEM image of

intrinsic stacking faults in a 6H-SiC crystal in which

the formation energy of SF is so low that wide SFs are

observed after plastic deformation.

Small-angle grain boundaries are imaged by TEM

as a densely arrayed dislocations. In some cases,

grain boundaries are visible as Moiré patterns of two

overlapping crystals. Modern TEM studies of planar

defects, however, are often conducted by imaging end-

on the defects by HRTEM. Recently, for example,

cross-sectional HRTEM imaging of epitaxial thin ﬁlms

(a kind of phase boundaries) has become a standard rou-

tine in assessment of these materials. Cross-sectional

HRTEM not only presents straightforward pictures for

nonspecialists but also provides quantitative informa-

tion that cannot be collected with conventional TEM.

In particular, atomic arrangements at grain boundaries

can be directly deduced by comparing end-on HRTEM

images and simulations. The density of stacking faults

can be evaluated by cross-sectional HRTEM even if the

density is too high for plan-view observations to be

possible.

X-Ray Topography (XRT)

Dislocations and stacking faults are observable also by

x-ray topography (XRT) based on essentially the same

principle in TEM, although there is some difference due

to differences in the optical constants between electrons

and x-rays. Roughly speaking, XRT images correspond

to dark-ﬁeld images in TEM. Figure 5.77 shows a trans-

mission XRT image of dislocations in a Si ingot crystal

introduced in the seeding process. Here the dislocations

are imaged as white contrasts. The important parame-

ter to be considered in interpretation of XRT images

is the product μt, where t is the sample thickness and

μ is the absorption coefﬁcient. If μt 1, we need the

dynamical theory to understand images correctly, but

if μt is of the order of unity or less, the kinemati-

cal theory is sufﬁcient, which is the case in Fig. 5.77

(μt ≈ 1fort = 0.6 mm). The mechanism of white dis-

location contrasts in Fig. 5.77 is essentially the same

as that of dark contrasts in TEM bright-ﬁlled images

due to the kinematical effect that the diffraction beam is

Part B 5.3

Nanoscopic Architecture and Microstructure 5.3 Lattice Defects and Impurities Analysis 257

5 mm

Fig. 5.77 A transmission x-ray-topographic image of dislocations in a Si ingot crystal introduced in the seeding process.

The sample thickness is 0.6 mm. (Courtesy of Dr. I. Yonenaga)

directly reﬂected from the close vicinity of the disloca-

tion cores where the Bragg condition is locally satisﬁed.

Figure 5.78 shows another transmission XRT image of

dislocations now in a plastically deformed GaAs crys-

tal. In this case, the dislocations are imaged as dark

contrasts. Though the sample thickness is 0.5 mm, even

smaller than the case of Fig. 5.77, the absorption co-

efﬁcient is much larger and as a result μt ≈ 10. The

anomalous transparency despite the large μt is owing

to a dynamical effect (Borrmann effect), the anomalous

transmission of the channeling Bloch wave. Although

the quantitative interpretation of the image needs the

dynamical theory, the origin of the dark dislocation

contrasts in this case is the loss of crystallinity in the

severely deformed regions that results in the reduction

of the diffraction intensity.

Scanning Electron Microscopy

in Cathodoluminescence Mode (SEM-CL)

Dislocations in semiconductors in many cases act as

efﬁcient nonradiative recombination centers. In such

cases, they are observed as dark spots or lines in

SEM-CL images when the matrix emits luminescence.

Figure 5.79 shows an SEM-CL image of an indented

CdTe surface and an OM image of the same area the

surface of which was chemically etched to reveal dislo-

cations after the SEM-CL image was acquired. In some

exceptional cases, the dislocations themselves emit light

which gives rise to bright contrasts. TV scanning allows

one to observe in situ the dynamical motion of disloca-

tions. Similar images may be obtained by using OM if

the defect density is sufﬁciently low.

1 mm

Fig. 5.78 An anomalous transmission x-ray topographic

image of dislocations in GaAs introduced by plastic defor-

mation. The sample thickness is 0.5 mm (Courtesy of Dr.

I. Yonenaga)

X-Ray Diffraction Analysis of Planar Defects

The density of planar defect such as stacking faults

can be assessed by quantitative analysis of the x-ray

diffraction proﬁle with proper corrections for instru-

mental and particle size broadening. The presence of

planar defects introduces phase shifts of scattering

Part B 5.3