Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing

Подождите немного. Документ загружается.

228 Part B Chemical and Microstructural Analysis

Fixed mirror

Light source

Movable

mirror

Half mirror

(beam splitter)

Δx

(Δx)

Fig. 5.32 Michelson-type interferometer used in Fourier

transform infrared (FT-IR) spectroscopy

the wavelength λ. In other words, when the light in-

put to the interferometer contains different spectral

components, the interference fringes or interferogram

(Fig. 5.33a), the temporal superposition of the mod-

ulated signals, constitutes the Fourier transform of

the whole spectrum. Conversely, the inverse Fourier

transform of the experimentally measured interfero-

gram provides the spectrum (Fig. 5.33b) without any

spectral dispersive apparatus. The FT spectroscopy is

advantageous in terms of the signal-to-noise ratio when

the detector noise is large and we need high spectral

resolution. The infrared (IR) spectroscopy is a typi-

cal case to which the FT scheme is most efﬁciently

applied.

Intensity

100 900

Time (rel. units) Wave number (cm

–1

)

Interferogram FT-IR spectrum

Fourier transform

800 3500 300110019002700700600500400300200

Polyethylene

Absorbance, transmission (arb. units)

(abs)

(sb)

a) b)

H n

Fig. 5.33a,b An example of FT-IR absorption spectroscopy. (a) An interferogram of transmission through a polyethylene

sample, (b) (sb) Fourier transform of the interferogram and (abs) the absorbance spectrum corrected for the instrumental

background (after [5.27])

Raman Scattering

Raman scattering is a generic term for inelastic scat-

tering of light but in most cases it refers to inelastic

scattering brought about by optical phonons (quan-

tized vibrations) in molecules and solids. While infrared

absorption originates from the polarization of the sub-

stance, Raman scattering originates from a modulation

of optical polarizability of the substance by phonons.

Therefore, the selection rule is different for the two phe-

nomena. In molecules, infrared absorption occurs when

the molecules have an electric dipole transition moment

in the polarization direction of the incident light, as in

the cases shown in Fig. 5.34. Raman scattering occurs

when a molecular vibration in a certain mode alters

the electronic distribution of the molecule (Fig. 5.34)

and consequently the optical polarizability for the in-

cident light. In solids, although the selection rules are

not as intuitive as for molecules, the principles are the

same. Due to this difference in the selection rules, in-

frared spectroscopy and Raman scattering spectroscopy

are complementary in studies of atomic vibrations in

matter.

In the energy diagram, the sequential two-photon

process in Raman scattering is depicted in Fig. 5.35,

which shows only the case of the Stokes shift, in which

a phonon mode of energy hΩ is excited and as a re-

sult the photon energy is decreased on scattering by

this amount. The broken line in Fig. 5.35a indicates

an intermediate virtual electronic state via which the

system evolves in the sequence of photon absorption

and emission. In contrast to infrared absorption, Raman

Part B 5.1

Nanoscopic Architecture and Microstructure 5.1 Fundamentals 229

+–+

Raman

: allowed : forbidden

Fig. 5.34 Selection rules of infrared absorption and Ra-

man scattering illustrated for molecules in various vibra-

tion modes

a) b)

Intermediate state

Vibronic ground state

hv–hΩ

hΩ

hv–hΩ

hΩ

Virtual Real

Fig. 5.35a,b Raman scattering process: (a) nonresonant,

(b) resonant, shown for the Stokes shift by exciting a single

phonon. hν and hΩ are the energy of the incident photon

and the phonon energy, respectively

scattering is a two-photon process and the scattering

signal is generally very weak. However, when the inter-

mediate electronic state is not virtual but really present

(Fig. 5.35b), Raman scattering occurs in a resonant

manner with the scattering intensity being substantially

enhanced (resonant Raman scattering). The minimum

content of Raman-active centers required is 0.01–1%

or > 10

−3

in nonresonant cases. When the cen-

ters to be detected are present in the surface layer of

samples, the sensitivity is further enhanced (up to 10

times) by employing the scheme of surface-enhanced

Raman scattering [5.28, 29], which exploits a dramatic

increase of the optical electric ﬁeld in the vicinity of

metallic nanoparticles such as Ag and Au.

Magnetic Resonance Spectroscopy

Experimental methods based on magnetic resonance of

nuclear or electronic spins are applied to the inves-

tigation of defects and impurities in solids, structural

analysis of molecules, and in some cases, microstruc-

ture analysis.

When electrons and nuclei have an angular mo-

mentum S (where  is Planck’s constant), a magnetic

moment

μ =γ S (5.16)

is associated with it. S stands for s = 1/2 for electronic

spins, for j for electronic orbital angular momenta, and

for I, various multiples of 1/2, for nuclear spins. The

coefﬁcient γ is called the magnetogyric ratio deﬁned by

γ ≡

2mc

, (5.17)

where g and m are the g-factor (a numeric constant in

the range 1–3 depending on the origin of the angular

momentum) and the mass of the particle, respectively,

and e is the electronic charge, and c the speed of light.

Quantum mechanically, a spin or a magnetic mo-

ment under a static magnetic ﬁeld of intensity B

(magnetic ﬂux density) has discrete eigenstates. For the

simplest case of S = 1/2, the spin has two states, as

shown by the energy level diagram in Fig. 5.36a, sep-

b) c)

hω

Fig. 5.36a–c Quantum-mechanical picture (a) and classi-

cal vector model (b,c of magnetic resonance illustrated for

an S = 1/2 system. In (a), since the Zeeman-split lower

spin state α, is more occupied than the higher state β,in

thermal equilibrium, the application of a resonant electro-

magnetic wave causes transitions between the two states,

resulting in a net energy absorption. Classically, (b) the

macroscopic magnetization M is the average of the spin

magnetizations precessing with random phase in thermal

equilibrium.

bunched and the resultant magnetization starts to ﬂips its

head down, tracing a spiral trajectory in real space

Part B 5.1

230 Part B Chemical and Microstructural Analysis

arated by an energy ω

where

=γ B

(5.18)

is called the Larmor angular frequency. In magnetic res-

onance experiments, the sample is further subject to

a small magnetic ﬁeld perpendicular to the static ﬁeld

and alternating at the Larmor frequency, which reso-

nantly induces transitions between the two states. In

Fig. 5.36a, the number of ﬁlled circles indicates the

population of the respective states. Since, in thermal

equilibrium, the lower energy state (up-spin state) is

more occupied than the higher energy state (down-spin

state), the spin system absorbs a net energy from the

electromagnetic oscillations.

Classically, a magnetic moment under a static

magnetic ﬁeld precesses around the axis of the

static magnetic ﬁeld (normally taken as the z-axis)

at the Larmor frequency, as shown schematically

in Fig. 5.36b. In thermal equilibrium, however, the

precession of the spins cannot be detected because

each precession is random (incoherent) and hence, in

macroscopic samples containing many spins, the mag-

netization of the spin assembly is averaged out leaving

only the z-axis component, due to the excess population

of up spins. An intuitive picture of magnetic resonance

is such that the spins become bunched coherently under

a resonant microwave and the resultant magnetization,

represented by a vector shown in Fig. 5.36c, ﬂips its

head down drawing a spiral trajectory. Although this

classical vector model is rarely used in electron spin

resonance (ESR) or electron paramagnetic resonance

(EPR), it is repeatedly applied to interpretation of nu-

clear magnetic resonance (NMR). (Although ESR and

EPR are often used interchangeably in textbooks, the

term ESR in this chapter refers to a generic methodol-

ogy including EPR.)

What makes magnetic resonance informative for

structural studies of materials is the interactions of var-

ious origins operating between spins. The magnetic

moments associated with spins exert an effective mag-

netic ﬁeld on the dipole moment of other spins (classical

dipole–dipole interaction). The Pauli principle gives

rise to a quantum-mechanical interaction between two

electronic spins (exchange interaction). The behavior of

a general system consisting of electron spins and nu-

clear spins interacting with each other is described by

the effective spin Hamiltonian formally written as

H = B



S−2SJ



S+SAI −B

+IJ

I +IQI +··· . (5.19)

Here S and I are now quantum operators of to-

tal electronic spins and nuclear spins, respectively.

The tensorial magnetogyric ratios γ



[slightly modi-

ﬁed from (5.17) by spin–orbit coupling, the detail of

which is given in Sect. 5.4.2]andγ

or the correspond-

ing tensorial g-factors describe the Zeeman splitting,

respectively, J



the direct exchange interaction between

spins (slightly modiﬁed by spin–orbit coupling), J

the

nuclear spin–spin indirect interaction, A the effect of the

environment of the spins (e.g., anisotropic crystal ﬁeld),

Q the nuclear quadrupole interaction between the elec-

tric quadrupole moment associated with I > 1/2 nuclei

and an electric ﬁeld gradient at the nuclear position. Due

to the large difference between the particle mass of elec-

trons and nuclei, γ



γ

. Therefore, electron spins feel

only small perturbations by nuclear spins, but the EPR

spectra exhibit quite informative ﬁne structures arising

mainly from the third term of (5.19). On the contrary,

since the presence of electronic spins has enormous ef-

fects on the nuclear spin states, NMR spectra become

complicated in paramagnetic samples.

In the absence of electronic spins, the interaction

of nuclear spins with the environment is so weak that

the nuclei have a long spin lifetime, a quantity express-

ing how long the spin coherence once established is

maintained as long as the nuclei are stationary in space.

In other words, the decrease of nuclear spin lifetime

with dynamic motion of the nuclei gives ample infor-

mation of the dynamics. This unique feature of NMR

provides the basis of NMR studies of impurity diffu-

sion in solids (Sect.5.3.1) and of molecular architecture

(Sect. 5.4.2).

There are many other experimental methods

that may be classiﬁed as magnetic resonance spec-

troscopy. Optically detected magnetic resonance

(ODMR) (Sect. 5.3.1), magnetic circular-polarized

emission (MCPE) (Sect. 5.3.1), and magnetic circular

dichroic absorption (MCDA) (Sect. 5.3.1) are optical

spectroscopic versions of EPR. Muon spin resonance

(μSR) (Sect. 5.3.1) and perturbed angular correlation

(PAC) (Sect. 5.3.1) may be regarded as NMR of

exotic or radioactive particles. However, these tech-

niques will be described in a more relevant section

(Sect. 5.3.1).

Electron Spectroscopy

Electron Energy-Loss Spectroscopy (EELS). Nowadays,

transmission electron microscopes are often equipped

with an electron energy spectrometer for routine anal-

ysis of electron energy loss. Like photons, electrons

injected into solid samples lose their energy by ex-

Part B 5.1

Nanoscopic Architecture and Microstructure 5.1 Fundamentals 231

citing quanta of various forms, but the main loss

arises from excitation of other electrons. Among them,

the excitation of plasmons with a loss energy of

≈20 eV is the most efﬁcient process, whereas this

is not the case in photoabsorption, determining the

limited penetration power of the electrons through

the sample. The plasmon energy is not sufﬁciently

sensitive to the material, so the plasmon loss does

not give signiﬁcant information other than the thick-

ness of the thin samples used for TEM observations.

If the energy of incident electrons exceeds the en-

ergy necessary for a core electron excitation, another

energy-loss mechanism takes place. Since the electron

energy used in TEM is high enough, the correspond-

ing thresholds are observed in the EELS spectrum,

which is a common technique for element analysis by

TEM.

X-Ray Electron Spectroscopy. On core excitations by

x-rays, electrons may be emitted from of the solid via

two different mechanisms. Direct photoelectron emis-

sion occurs when the x-ray photon energy is high

enough to excite the core electrons to vacuum levels

(electronic energy levels just outside the solid surface).

The energy of the photoelectrons measured relative to

the Fermi level of the sample, therefore, directly reﬂects

the energy of the core electrons. Another mechanism is

Auger electron emission that occurs when a hole gen-

erated at the core level is annihilated with an electron

in an upper level. The energy released on the electron–

hole annihilation is spent either by creation of a photon

(x-ray ﬂuorescence) or an excitation of another elec-

tron (Auger electron) to a vacuum level. The processes

are competitive but the Auger process dominates in

elements lighter than Z ≈ 30. Whether through direct

photoelectron emission or Auger emission, when the

energy of the electrons is of the order of 10 eV, the

electronic mean free path is so short due to the plas-

mon loss that they cannot escape from deep positions

in the sample. For this reason, x-ray photoemission

spectroscopy (XPS) and Auger electron spectroscopy

(AES) are surface-sensitive techniques, being power-

ful for studies of surfaces but not suitable for bulk

samples.

Mechanical Spectroscopy

Mechanical spectroscopy [5.30] is the generic term

for characterization methods of anelastic behavior such

as elastic aftereffect, internal friction and ultrasonic

attenuation. Anelastic spectroscopy is a synonym of me-

chanical spectroscopy. In the elastic range, the strain

response to applied stress is composed of the (instanta-

neous) elastic strain ε

and the (delayed) anelastic strain

, where the ratio ε

/ε

is indicative of anelasticity.

The measurement time scale is quasistatic for elastic

after effect, below ≈ 10

Hz for internal friction and

above ≈10

Hz for ultrasonic attenuation. Interaction

of acoustic waves with phonons is out of the present

scope. Thermoelastic relaxation is associated with the

adiabatic temperature change induced by application

of a stress and can be commonly observed in solid

materials, but its magnitude is negligibly small except

in the vicinity of the resonant condition. Mechanical

spectroscopy can be applied to detect the recoverable

motions of/in atoms, lattice defects, interfaces, mag-

netic domain walls and so on when they modify the

strain response. The value of ε

/ε

is a function of

the anelastic strain for each process and the concentra-

tion of participating agents, which may be a function of

the strain amplitude ε, frequency f and temperature T .

For example, the value of ε

/ε

at room tempera-

ture is of the order of 10

−7

in silicon single crystals,

−1

in highly damping metals and more than unity in

polymers.

The anelastic relaxation is characterized by the re-

laxation time τ and ε

/ε

, where the relaxation peak

exhibits a maximum at ωτ =1(ω = 2π f ). Thermally

activated anelastic relaxation is studied as a function

of temperature or frequency. The elastic aftereffect

is isothermally measured as a function of elapsed

time, where τ and ε

/ε

at a given temperature are

found directly. In subresonance measurements, inter-

nal friction is isothermally measured as a function of

frequency, e.g., in the range between 10

−3

and 10 Hz.

These methods are applicable for ε

/ε

> 10

−5

be-

cause of limitations on experimental accuracy. It is

emphasized that these methods can also be applied

to materials with ε

/ε

> 1. The resonance meth-

ods are applicable to cases of ε

/ε

< 10

−1

, where

internal friction is measured as a function of tem-

perature. These methods are applicable to thin plates

or rod specimens. Ultrasonic attenuation is applica-

ble to bulky specimens, where the specimen length

should be longer than the pulse length. In Sects. 5.3.1

and 5.3.2, some more detail of internal friction is

described.

Part B 5.1

232 Part B Chemical and Microstructural Analysis

5.2 Crystalline and Amorphous Structure Analysis

The subject covered in this section will be structural

analysis of ordinary metallic and nonmetallic crystalline

solids, molecular crystal, liquid crystals, amorphous

solids, and quasicrystals. The subsections are divided

according to the extent of structural order in space.

Surface-speciﬁc problems are beyond the scope of this

chapter.

5.2.1 Long-Range Order Analysis

Single Crystal Analysis

As mentioned in Sect. 5.1.1, the structure factor F(K)

in wavenumber space is related to the electronic den-

sity ρ(r) in real space through a Fourier transformation.

Since the electrons are concentrated at the atomic

positions, knowing the electronic density ρ(r)isto

know the crystal structure. In principle, therefore, the

crystal structure can be deduced by the inverse Fourier

transformation of the structure factors if known exper-

imentally. In practice, however, the only quantities we

can measure in experiments are not F(g) = F

exp



iφ



but

F(g)

(hereafter, reciprocal lattice vectors g in

structure factors implicitly indicate the structure fac-

tors integrated over the broadening width), which means

that we lack the knowledge of the phase factors φ

calculate the electronic distribution immediately. This

phase problem is the main difﬁculty in structural anal-

ysis of x-ray diffraction, to which much effort has been

devoted. The standard analytical methods to tackle this

problem are the direct method, the heavy atom method

and the anomalous dispersion method.

The direct method is based on a general relation

(Sayre’s formula)

F(h) =a



F(g)F(h−g) a : a real coefﬁcient

(5.20)

which holds for arbitrary structure factors. In many

practical cases, diffraction intensities are concentrated

in a limited number of diffraction spots. In the sim-

plest case, where a single term containing a speciﬁc g

predominates in the sum,

F(h) ≈aF(g)F(h −g) , (5.21)

we have a phase relationship of

≈φ

+φ

h−g

(5.22)

approximately. Thus, having assumed two phase values,

one could evaluate the other and so on, successively. In

the actual procedure, starting with an initial set of phase

values for dominant diffractions, one repeats an iterative

procedure to recalculate the phase values until conver-

gence is achieved. Such procedures are attempted for

many initial sets of F(g) = F

exp



iφ



, or model struc-

tures that yield the sets, until the best ﬁt with experiment

is achieved.

The heavy atom method is based on the fact that

the atomic scattering factor f (K) increases with the

number of electrons in the atom and hence the atomic

number. This method can be efﬁcient in those crystals

containing metal complexes in which the structure fac-

tors are determined mainly by the arrangement of the

heavy metal atoms. Exploiting this situation, we could

estimate the approximate positions of the heavy atoms

in the unit cell. The experimentally measured inverse

Fourier transform of |F(g)|

is called the Patterson

function, the autocorrelation function of the electron

density ρ(r),

P(u) =



ρ(r)ρ(r +u)dv. (5.23)

Therefore, the Patterson function has strong peaks at

relative positional vectors connecting two heavy atoms

in real space. From these peaks one could deduce the

real positions of only the heavy atoms in the unit cell

(for more details, see the relevant textbooks [5.8]). The

heavy atoms may be intentionally introduced in the pro-

cess of crystal growth or in the synthesis of chemicals

for macromolecules that are to be grown into crystalline

samples. Chemical substitution is a method commonly

used in structural analysis of biomolecules (Sect. 5.4.1).

Instead of substituting atoms, in some cases the

anomalous dispersion effect can be used. Anomalous

dispersion is a phenomenon in which the complex

atomic structure factor changes considerably at wave-

lengths around the core excitation edge. Therefore, if

we use x-rays of an appropriate wavelength, we can

effectively substitute atoms with different atomic scat-

tering factors. Since the advent of synchrotron radiation

sources, it has become possible to use strong monochro-

matic x-rays tunable to a speciﬁc wavelength so that the

anomalous dispersion method now constitutes a power-

ful technique applicable to many materials.

In addition to the phase problem, measurements of

obs

(K) for only a limited number of K vectors could

lead to spurious results due to a cut-off effect in the

inverse Fourier transformation. These difﬁculties are

now being overcome by the application of the maxi-

Part B 5.2

Nanoscopic Architecture and Microstructure 5.2 Crystalline and Amorphous Structure Analysis 233

mum entropy method (MEM)[5.31], a state-of-the-art

technique that allows very precise analysis of diffrac-

tion data based on the method of least presumption and

structural models of the crystal.

Regarding the sample, the availability of a single

crystal is an essential prerequisite. As shown in (5.8),

the intensity of the diffracted x-rays depends linearly

on the number of atoms or the sample volume, in other

words, it decreases rapidly as the third power of the

sample dimension. If we use a conventional sealed x-ray

tube, the size of single crystals must be larger than

0.1 mm, but if a synchrotron radiation source is avail-

able, the sample size may be reduced by one order of

magnitude. The crystal quality must be high enough that

peak broadening due to imperfections is small enough

to allow peak separation. This is of particular impor-

tance in molecular crystals because the lattice constant

of molecular crystals is likely to be so large that the

diffraction peaks crowded one another.

The samples are mounted on a goniometer as shown

in Fig. 5.37 and rotated around three Eulerian axes. Usu-

ally the ω–2θ (θ–2θ) scan scheme is employed: the

angles φ and χ are adjusted so that the sample can

be rotated around a zone axis coincident with the ω-

axis by increasing the incidence angle θ step by step

while simultaneously rotating the detector by 2θ so as

to maintain specular reﬂection conditions.

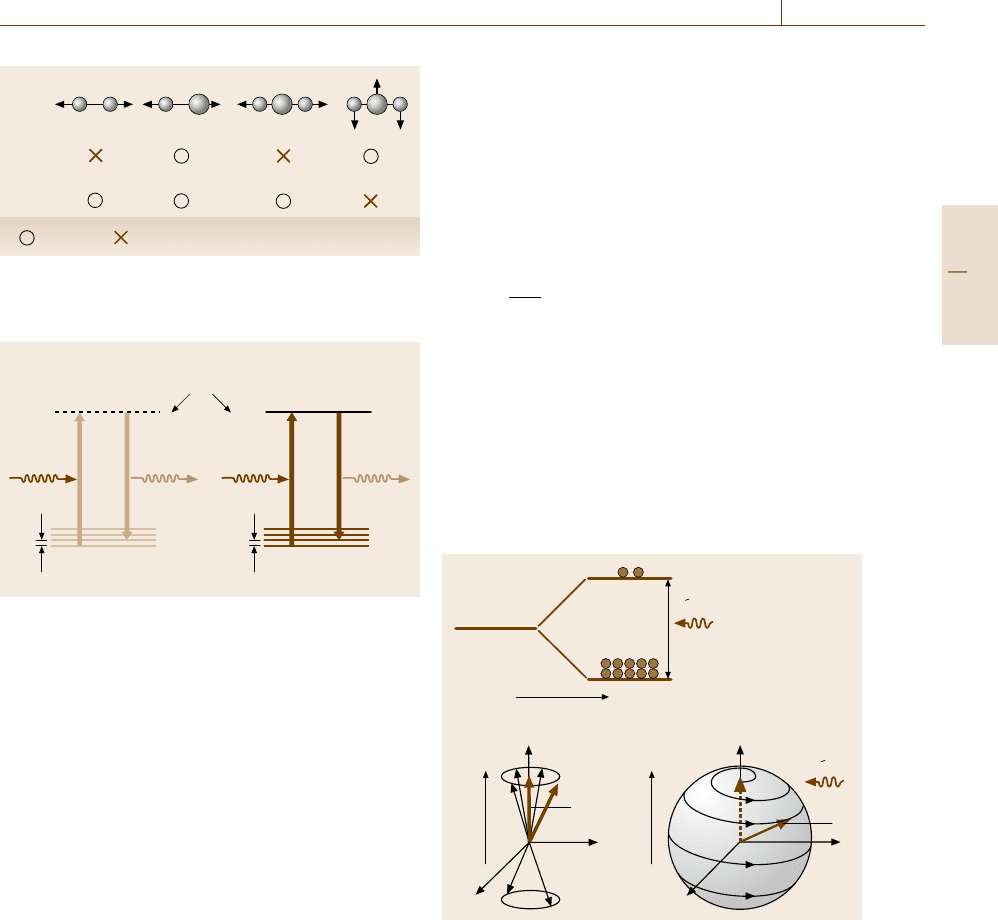
Powder Diffraction

Single crystal diffraction experiments using a relatively

large crystal give a data set from which we could deduce

the crystal structure with high accuracy. However, since

most materials of technical interest cannot grow to large

single crystals, one has to resort to the use of powder

samples consisting of small crystallites. At this point,

one might suspect that, instead of using crystalline sam-

Beam source

Detector

2θ

Fig. 5.37 Rotation angles in a four-circle goniometer

ples, one could use amorphous samples as the extreme

of small crystallites. This view is totally wrong because

for the Bragg diffraction, which is a consequence of

constructive interference, to occur, the crystal must have

a ﬁnite size. For crystal structure determination by pow-

der diffraction, the crystallite size should preferably be

larger than the micron scale. X-ray analysis of short-

range order in amorphous solids will be described in

Sect. 5.2.3.

In powder diffraction, the reciprocal lattice is ran-

domly oriented with respect to the incident x-ray beam

and the Ewald sphere. As a consequence, the x-ray

diffraction by crystallographically equivalent lattice

planes occurs in directions forming a cone with a com-

mon diffraction angle 2θ, as illustrated in Fig. 5.38a.

The diffraction pattern thus obtained consists of rings

(Debye rings) of different diameters the values of

which are related to the interplanar spacings in the

Bragg condition (5.1). The historical method of study-

ing the Debye rings is to use a Debye–Scherrer camera

(Fig. 5.38b) in which a slice of Debye rings is recorded

on a strip of x-ray ﬁlm placed around the sample. In

modern experiments, the x-ray ﬁlm is replaced with an

x-ray detector turning on a diffractometer (Fig. 5.38c).

If the Debye rings or diffraction peaks are properly in-

Diffraction

cone

2υ

X-ray film

2υ

Counts

Fig. 5.38 (a) Ewald construction for powder diffraction,

(b) Debye–Scherrer camera and (c) diffraction proﬁle

recorded by a diffractometer

Part B 5.2

234 Part B Chemical and Microstructural Analysis

dexed with knowledge of the crystal structure and the

extinction rule, the lattice parameter of the crystal can

be determined with accuracy higher than 10

−6

The sample requirements for powder diffraction

measurements are as follows.

1. The sample must be an assembly of crystallites each

smaller than ≈10 μm (ideally ≈3 μm).

2. Individual crystallites must be oriented randomly.

Condition 1 is important because, if exceptionally

large crystallites are present, they introduce bright spots

in the Debye rings (as exempliﬁed in Fig. 5.99), which

introduces a spurious diffraction proﬁle. Similarly, if the

orientational randomness is lost, it is impossible to mea-

sure correct proﬁles. In such cases, the sample must

be rotated to remove such artifacts. For assessment of

orientationally textured materials see Sect. 5.5.1.

The main drawback of the powder diffraction

method compared to methods using single crystals is

the overlap of diffraction peaks that prevents the ac-

curate determination of the integrated intensity of each

reﬂection and hence the structure factor. The Rietveld

method, which allows an effective separation of these

overlapping peaks, is a standard technique routinely

used nowadays in the analysis of powder diffraction

data. For the phase problem, the power of MEM

(Sect. 5.2.1) in the analysis of x-ray powder diffraction,

combined with the Rietveld method, has also been pro-

gressively discovered [5.33]. Using powder diffraction,

one can determine the structures of considerably large

molecules such as metmyoglobin, the single crystal unit

cell of which contains two molecules (≈ 5000 atoms)

and ≈800 waters [5.34].

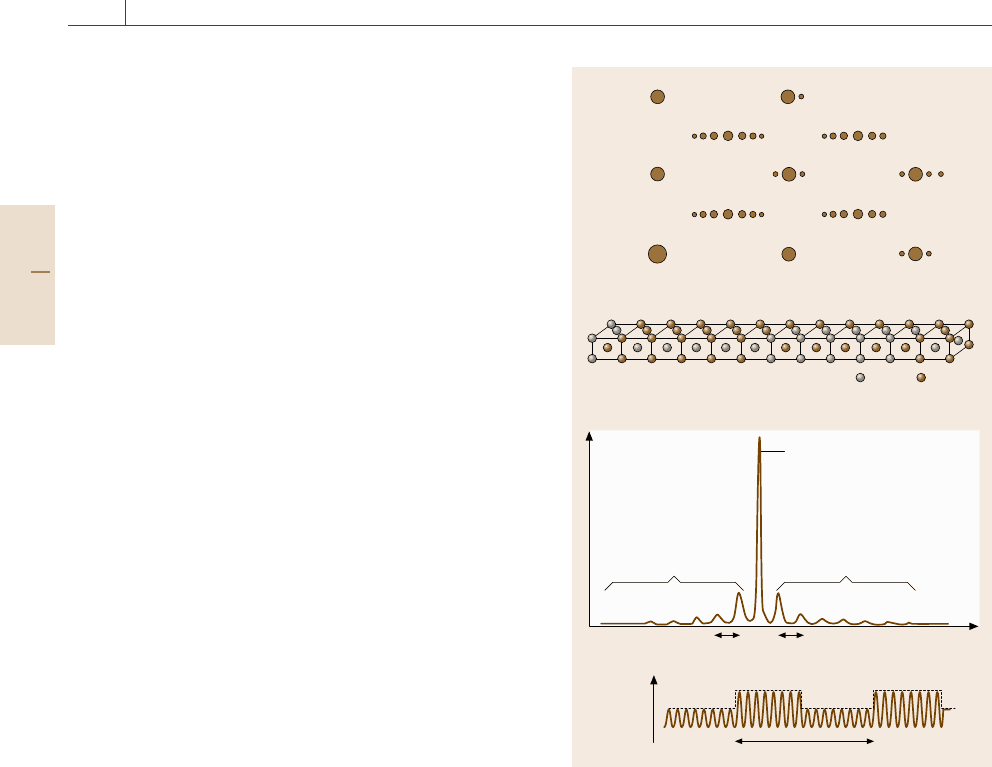
Selected Area Diffraction (SAD)

The general merit of using TEM is that one can in-

vestigate solid structures at a medium-scale range, but

most of this matter is more relevantly addressed in

the section on microstructure analysis (Sect. 5.5). Se-

lected area diffraction in TEM corresponds to single

crystal diffraction of monochromatic x-rays, displaying

a two-dimensional projection of the reciprocal lattice

in the zeroth-order Laue zone (ZOLZ). In this re-

gard, there is no great difference in principle between

x-ray diffraction and SAD. Nevertheless, the real-time

graphic presentation of the reciprocal lattice in SAD

may give us more chance to notice subtle changes in

crystal ordering visually. Figure 5.39ashowsaSAD

pattern of an CuAu stoichiometric alloy ordered with

a superperiodicity (b). The SAD pattern is characterized

by satellite spots which are absent when the crystal is

Diffraction intensity

400

200

000

Satellites

1/Λ

Š (r)

1/Λ

Satellites

Bragg

reflection

420

310 330

110 130

220 240

040

AuCu

020

Fig. 5.39a–d Superlattice reﬂections (a) in the super-

periodic ordered phase of CuAu stoichiometric alloy.

(b) After [5.32] and Fourier transform (c) of a periodically

modulated sinusoidal wave (d)

ordered but not in the long range. The origin of the satel-

lites may be understood by examining Fig. 5.39c, which

illustrates the Fourier transform of a periodically modu-

lated sinusoidal wave (d) that mimics the superperiodic

structure.

Similar satellites can be observed by x-ray diffrac-

tion of artiﬁcial superlattice thin ﬁlms grown by the

molecular beam epitaxial method. For the superlat-

tice spots to be observed, x-ray diffraction experiments

are conducted in a reﬂection conﬁguration, where the

x-rays incident to the front side of the ﬁlms are

Bragg reﬂected by lattice planes that are parallel to

the ﬁlm surface, as shown schematically in Fig. 5.2

(Sect. 5.1.1).

Part B 5.2

Nanoscopic Architecture and Microstructure 5.2 Crystalline and Amorphous Structure Analysis 235

5.2.2 Medium-Range Order Analysis

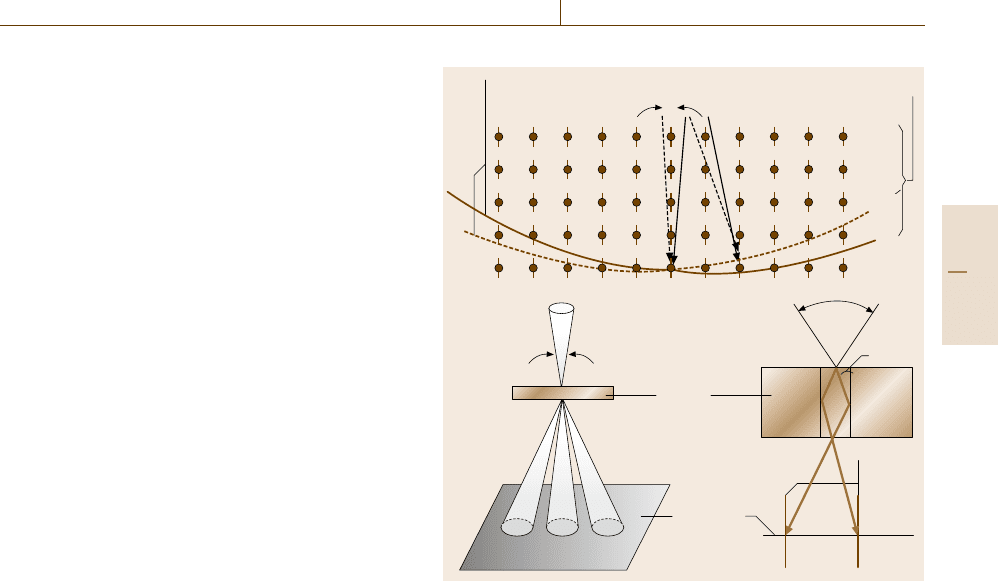
Convergent Beam Electron Diffraction (CBED)

Although the selected area diffraction (SAD) (Sects.

5.1.2 and 5.2.1)inTEM gives us structural informa-

tion of the local parts (> 0.5 μm in size) of the sample

selected by the objective aperture, the crystallographic

information is limited compared with x-ray diffraction.

The convergent beam electron diffraction (CBED)is

even more informative than x-ray diffraction in some

cases. In contrast to the parallel electron beam used in

SAD, the electron beam used in CBED is focused onto

a sample with a convergence semi-angle α>10 mrad.

Figure 5.40 illustrates how CBED patterns are formed

in reciprocal space (a) and in real space (b). The

beam convergence not only improves the spatial res-

olution down to tens of nanometres but also changes

substantially the information contained in the diffrac-

tion patterns if the sample thickness t is larger than

the extinction distance ξ

, the case in which the dy-

namical effect (Sect. 5.1.2) must be taken into account.

Figure 5.41 shows a schematic CBED pattern: the zero-

order Laue zone (ZOLZ) diffraction spots in SAD are

observed as disks in CBED. If the convergence angle 2α

is large enough, diffraction is also excited from higher-

order Laue zones (HOLZ) outside of the ZOLZ disks

(HOLZ is the general term for the ﬁrst-order Laue zone

(FOLZ), the second-order Laue zone (SOLZ), and so

on). An effect of multiple reﬂections in CBED is the

characteristic dynamical contrasts within the disks that

are absent when t <ξ

. In kinematical x-ray diffraction,

centrosymmetric crystals and noncentrosymmetric ones

cannot be distinguished because (h, k,)and(

)

diffraction spots are, in any case, observed with the

same intensity. In CBED, however, the diffraction pat-

tern exhibits the same symmetry as the point group of

the crystal due to the dynamical effect, so that one may

fully determine the point group symmetry from a set of

CBED patterns obtained for different zone axes.

Measurements of lattice parameter by SAD is not

as accurate (≈ 2%) as in x-ray diffraction even if the

camera length, which directly affects the diameter of

the diffraction rings on the screen, is calibrated care-

fully by using a reference crystalline powder (e.g., Au).

However, the accuracy could be enhanced to ≈ 0.2%

by measuring the positions of sharp CBED Kikuchi

lines, another effect of dynamical diffraction in CBED.

When the convergence semi-angle α is larger than the

Bragg angle θ

(Fig. 5.40c), some electrons in the beam

may already satisfy the Bragg condition and hence be

reﬂected by the net planes to form Kikuchi lines sim-

Ewald

sphere

HOLZ

TOLZ

SOLZ

FOLZ

ZOLZ

Sample

2α

Back focal

plane

Kikuchi

lines

Fig. 5.40a–c Convergent beam electron diffraction (CBED)inre-

ciprocal space (a) and in real space (b).Ifα>θ

(Bragg angle),

CBED Kikuchi lines are formed (c)

ilar to those also observed in SAD.However,while

the Kikuchi lines in SAD originate from inelastic scat-

tering of incident electrons, the CBED Kikuchi lines

are formed by elastically scattered electrons. There are

twotypesofCBED Kikuchi lines, those bisecting each

ZOLZ disk (ZOLZ Kikuchi lines) and those arising

from HOLZ diffractions (Fig. 5.41). The Kikuchi lines

of particular importance here are the deﬁcient (dark)

Kikuchi lines observed within the direct (0, 0, 0) disk,

which have their origins in the HOLZ Kikuchi lines.

The positions of the HOLZ Kikuchi lines are more sen-

sitive to lattice strain than ZOLZ Kikuchi lines because

the larger |g|=1/d (d: interplanar spacing), the larger

its shift Δ|g|=−(Δd/d)|g|, which means the higher

sensitivity to strain Δd/d. The sharpness of the CBED

Kikuchi lines due to the smallness of the sampled area

also serves to enhance the strain sensitivity.

Methods for Paracrystalline Solids

The term paracrystal is used as a model of disorder in

crystalline solids. In this chapter, we use this term in

a broader sense to mean materials that are intermediate

between three-dimensionally periodic crystals and com-

Part B 5.2

236 Part B Chemical and Microstructural Analysis

HOLZ

reflections

Deficient

HOLZ

Kikuchi lines

ZOLZ disks

ZOLZ

Kikuchi

lines

(0, 0, 0) Disk

Fig. 5.41 A schematic CBED pattern featured by zero-

order Laue zone (ZOLZ) disks, deﬁcient HOLZ Kikuchi

lines in the direct (0, 0, 0) disk, and reﬂections from higher-

order Laue zones (HOLZ)

pletely amorphous structures. Most of the largest size

macromolecules are polymers which are formed by the

linear repetition of a group of atoms called a monomer.

A polymer has no ﬁxed conﬁguration but takes an al-

most inﬁnite variety of forms. Due to the ﬂexibility of

Crystal Smectic-A Smectic-C Nematic Amorphous

Fig. 5.43 Liquid crystal phases and their diffraction patterns (schematic)

Crystalline region Amorphous region

Fig. 5.42 Structure of polymer solid with coexisting crys-

talline and amorphous domains

polymeric chains and the tendency for mutual entangle-

ment, polymers are likely to solidify in an amorphous or

glassy form and are difﬁcult to crystallize perfectly. So

it is common that the ordered structure, if present, ex-

tends only to a limited range, as illustrated in Fig. 5.42.

For the assessment of the medium-range order, one of

the most common methods is to use interference optical

microscopes, in which phases having different optical

properties in terms of refractive index, birefringency,

the rotary power, etc. are imaged as different contrasts

or colors.

Between completely three-dimensional crystals and

glasses, some molecular solids have structures in which

Part B 5.2

Nanoscopic Architecture and Microstructure 5.2 Crystalline and Amorphous Structure Analysis 237

Fig. 5.44a,b SAD pattern of a quasicrystal (a) and the

model structure (b). Courtesy of Dr. K. Suzuki

the crystalline order is lost in some dimensions. Solids

belonging to this category are called liquid crystals.

The molecules in liquid crystals are commonly elon-

gated rigid rods with a typical length of ≈2.5nm and

a slightly ﬂattened cross section of 0.6nm×0.4nm.

The upper drawings in Fig. 5.43 show various forms

of liquid crystals in different degrees of order. The

crystalline phase on the left and the amorphous phase

on the right are completely ordered and disordered,

respectively, in terms of both molecular position and

orientation. In the so-called nematic phase in between,

the molecules are orientationally ordered but position-

ally disordered, and in smectic phases, the molecules

are orientaitonally ordered forming layers but the mo-

lecular positions are random within each layer. The

lower drawings in Fig. 5.43 illustrate the schematic

x-ray diffraction patterns of the aforementioned phases.

Thus, we may judge the phase from its characteristic

diffraction pattern.

Quasicrystals are noncrystalline solids condensed

with no periodicity that are not amorphous but that have

regularity different from crystals. Quasicrystals consist

of unit cells with ﬁve-fold symmetry which is incom-

patible with any crystalline long-range order. In spite

of the absence of crystalline order, however, quasicrys-

tals exhibit clear diffraction, as demonstrated by the

SAD pattern in Fig. 5.44a. This is due to the fact that,

even if the crystalline periodicity is absent, there are

atomic net planes regularly spaced as one may ﬁnd in

the model structure of a two-dimensional quasicrystal

showninFig.5.44b.

5.2.3 Short-Range Order Analysis

Diffraction Methods

Although the atomic arrangement in amorphous solids

is extremely disordered, it is not completely random as

in a gas phase but preserves a short-range order to some

extent. This is evidenced by halo diffraction rings from

amorphous solids, as shown in Fig. 5.45. For amorphous

solids, the intensity of the diffracted wave is simply

givenby(5.6) where the unit cell extends over the whole

solid. Hence

I(K) = I





(K)exp



iK ·r





= I



m,n

(K) f

(K)exp

[

iK ·(r

−r

)

]

(5.24)

For single component solids ( f

= f

≡ f ) consist-

ing of N atoms, some calculations show that

I(K)/N − f

=4π

∞



r [ρ(r) −ρ

] sin Kr dr ,

(5.25)

where ρ(r) is the radial distribution function, which is

deﬁned as the mean density of atoms located at dis-

tance r from an atom, and ρ

denotes the average

density of atoms. The above equation means that the

Part B 5.2