Цыпкин Я.З Основы теории автоматических систем

Подождите немного. Документ загружается.

СТРУКТУРЫ

АВТОМАТИЧЕСКИХ

СИСТЕМ

[ГЛ.

Условие воспроизведения приводит к образованию дополни-

тельного канала, передаточная функция которого

(p)

(6.42)

%б(р)

(P)

постоянна.

Благодаря этому Z(p) становится равным

FQ{P),

И,

значит,

Х(р)=

0. В этом

случае

система работает как разомкну-

тая.

Роль обратной связи

здесь сводится к уменьше-

нию

всех

дополнительных

изменений

в системе. Отсю-

да и название системы: разо-

мкнутый цикл — преобразо-

вание задающего воздей-

ствия,

замкнутый цикл —

уменьшение влияния различ-

ных дополнительных изме-

нений

в системе.

разомкнуто-замкнутой

системе близка так назы-

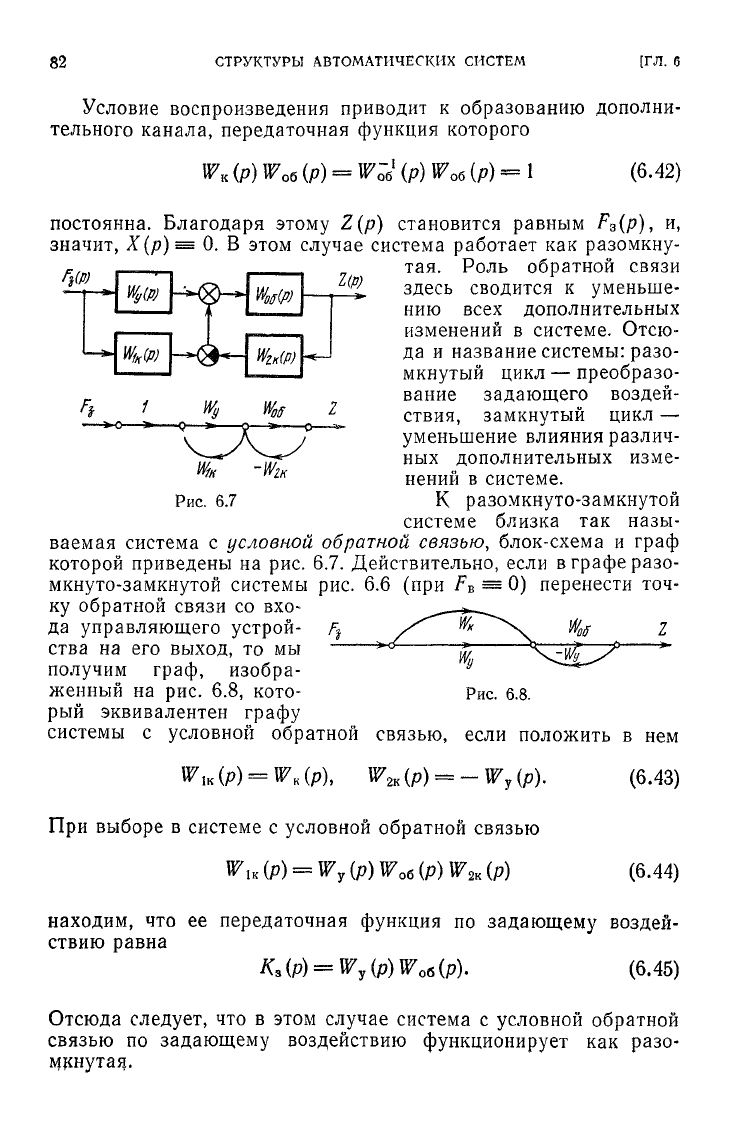
ваемая система с

условной

обратной

связью,

блок-схема и граф

которой приведены на рис. 6.7. Действительно, если в графе разо-

мкнуто-замкнутой системы рис. 6.6 (при

0) перенести точ-

ку обратной связи со

вхо-

да управляющего устрой-

/^ /^ % ^\

ства на его выход, то мы

получим граф, изобра-

женный

на рис. 6.8, кото-

рый

эквивалентен графу

системы с условной обратной связью, если положить в нем

Рис. 6.8.

R^IK

(Р)

(p),

(p)

-W

(p).

(6.43)

При

выборе в системе с условной обратной связью

(p) =

(p)

(6.44)

находим, что ее передаточная функция по задающему воздей-

ствию равна

(p)

(p)W

(p).

(6.45)

Отсюда

следует,

что в этом

случае

система с условной обратной

связью по задающему воздействию функционирует как разо-

вднута*?.

6.51

КОМБИНИРОВАННАЯ

РАЗОМКНУТО-ЗАМКНУТАЯ

СИСТЕМА

6.5. Комбинированная разомкнуто-замкнутая система

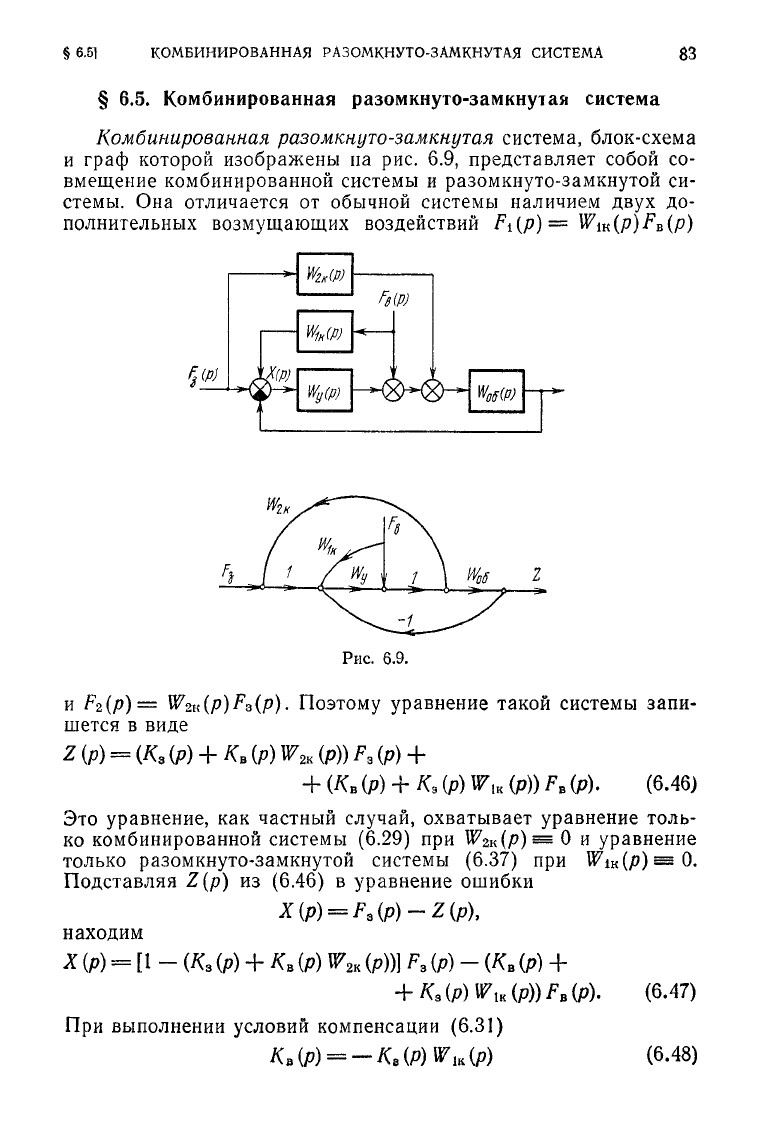
Комбинированная

разомкнуто-замкнутая

система, блок-схема

граф которой изображены па рис. 6.9, представляет собой со-

вмещение комбинированной системы и разомкнуто-замкнутой си-

стемы. Она отличается от обычной системы наличием

двух

до-

полнительных возмущающих воздействий

Fi(p)=

(p)F

(p)

(p)=

W2K{P)FQ(P).

Поэтому уравнение такой системы запи-

шется в виде

(р)

(К,

(Р)

(р)

(p))

(p) +

(К

(р) +

(p)

(p))

(p). (6.46)

Это уравнение, как частный случай, охватывает уравнение толь-

ко

комбинированной системы (6.29) при

№

к(р)=

0 и уравнение

только разомкнуто-замкнутой системы (6.37) при

(/7)^O.

Подставляя Z(p) из (6.46) в уравнение ошибки

находим

X (р)

[1 -

(К

(р) + К» (р)

(p))]

(p) - {К. (Р) +

(

(P))F

(P).

(6.47)

При выполнении условий компенсации (6.31)

(p)

-K

(P)W

(p)

(6.48)

СТРУКТУРЫ

АВТОМАТИЧЕСКИХ

СИСТЕМ

ГГЛ.

и воспроизведения (6.43)

Ks(p)

(P)W

(P)=1

(6.49)

или,

как

было показано

в §§

6.3

6.4,

(6.34), (6.41),

если

(p)^W;

(p)

(6.50)

(P)-W~

]

(p)

(6.51)

ошибка

становится тождественно равной нулю,

Х(р)

(6.52)

при

любых задающих и возмущающих воздействиях.

6.6. Общие уравнения автоматических систем

Рассмотренные выше автоматические системы

могут

быть

описаны

общими уравнениями относительно изображений. Обо-

значим

через

(р) =

Кэ

(р) +

Кп

(Р)

(p)

(6.53)

Kl (р) =

К*

(р) +

(p)

(6.54)

общие передаточные функции по задающему и возмущающему

воздействиям. В частных случаях при

(p)s=0

либо

И?2к(р)

£==

0 мы получаем передаточные функции разомкнуто-замкнутой

либо комбинированной системы, а при

(p)

—

передаточную функцию системы с внутренней положительной

обратной связью и обычной системы. Поэтому общее уравнение

автоматических систем относительно изображения выходной ве-

личины

можно записать в виде

(р) = Kl (p)

(p) + Kl (p)

(p),

(6.55)

а общее уравнение автоматических систем относительно изобра-

жения

ошибки — в виде

X (р)

- Kl (р))

/ч

(р) - Kl

(P)

(p).

(6.56)

Здесь

- Kl (р)

1 -

Кг

(Р) ~

(p)

(p) (6.57)

Kl (р)

К,

(р) +

(P)

(p)

(6.58)

— передаточные функции ошибки по задающему и возмущаю-

щему воздействиям.

ЗАДАЧИ

Автоматические системы называются

инвариантными,

если

их ошибка тождественно равна нулю при любых задающих и

возмущающих воздействиях.

Как

видно из общего уравнения (6.56),

условием

инвариантности

автоматической

системы

являет-

ся

тождественное

равенство

нулю

передаточных

функций

ошибки

по

задающему

возмущающему

воздействиям:

—

/С2

(р)

0, (6.59)

/С2(Р)^О.

(6.60)

В §§ 6.1, 6.2 были приведены частные случаи условий инва-

риантности

для обычной системы (6.7), системы с внутренней

положительной обратной связью

(6.20)

или (6.21), системы с

моделью объекта (6.25). Общие условия инвариантности (6.59),

(6.60)

представляют собой не что иное, как условия инвариант-

ности

комбинированной разомкнуто-замкнутой системы (6.48),

(6.49)

или (6.50), (6.51). Условия инвариантности (6.60),

(6.59)

состоят из

условия

компенсации

— тождественного обращения в

нуль передаточной функции ошибки по возмущающему воз-

действию и

условия

воспроизведения

—

тождественного обра-

щения

в нуль передаточной функции ошибки по задающему

воздействию. Если в автоматической системе выполняется какое-

либо одно из этих условий, то систему можно назвать

частично

инвариантной.

Примерами частично инвариантных систем яв-

ляются комбинированная система — при выполнении условия

компенсации

(6.34)— и разомкнуто-замкнутая

система

—

при

выполнении

условия воспроизведения

(6.39)

или (6.42).

Инвариантные

частично

инвариантные

системы

предста-

вляют

собой

идеальные

системы.

По

причинам, которые мы выясним далее, эти системы, как

правило,

физически нереализуемы. Однако знакомство с такими

идеальными системами весьма важно, так как они определяют

тот предел, к которому

следует

приближаться при желании син-

тезировать высококачественные системы с

учетом

реальных воз-

можностей и ограничений.

Задачи

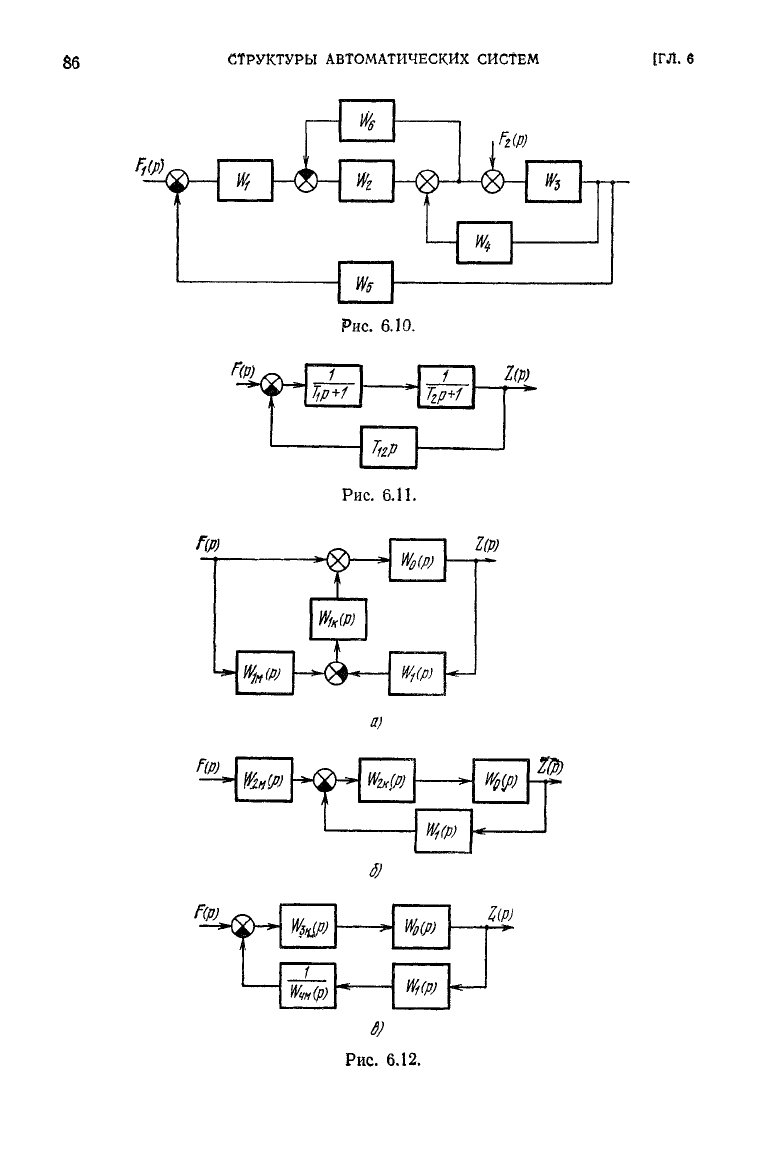
6.1.

Показать,

что передаточные

функции

замкнутой системы (рис. 6.10)

по

отношению

к задающему

f\(t)

возмущающему

(f)

воздействиям

равны

соответственно

(п)

(р)

41 W

1 +

(р)

(р) +

(p)

(р) +

(p)

(р)

Гз

(р)

(р) '

(р) (1 +

(P)

(p))

КР)

И^з

(Р)

(р) +

(p)

(р) +

(p)

(р)

(р) '

СТРУКТУРЫ

АВТОМАТИЧЕСКИХ

СИСТЕМ {ГЛ. 6

ftp)

Рис.

6.10.

Tfp+f

TfzP

TzP+1

Z(P)

Рис.

6.П.

(р;

—^

Щ(Р)

Zip)

ftp)

ЩФ)

т>

(p)

Щ(Р)

д)

Рис.

6.12.

ЗАДАЧИ

6.2. Показать,

что

система

обратной связью

на рис. 6.11

эквивалентна

электрической цепи

на рис. 5.22.

6.3. Показать,

что

структурные схемы

на рис. 6.12, а,

б,

эквивалентны,

если

(p)

(р)

(p)

(р),

6.4. Показать

для

этих

же

структурных схем,

что

если элементы

пере-

даточными функциями

(p),

W2x(p)

№зк(р)

имеют достаточно большие

коэффициенты

усиления

W\(p)

1, то для рис. 6 12, а К(р)

(p),

для

рис.

6.12,6

К(р)

u(p)

для рис. 6.12,0

К(р)

W*u(p).

Глава

ЧУВСТВИТЕЛЬНОСТЬ

АВТОМАТИЧЕСКИХ

СИСТЕМ

7.1.

Понятие

чувствительности

Чувствительность автоматических систем характеризует влия-

ние

изменений параметров элементов

на их

свойства. Вариация

элемента автоматической системы приводит

изменению

его пе-

редаточной функции,

это

свою очередь вызывает изменение

передаточной функции всей замкнутой автоматической системы,

а значит,

конечном итоге,

изменение величин, характеризую-

щих

ее

состояние.

Для

количественного

учета

всех

этих измене-

ний

служат

функции чувствительности

т//С

(р)

п п

Часто удобнее рассматривать

логарифмическую

функцию

чув-

ствительности,

или

просто чувствительность

(p)

передаточ-

ной

функции замкнутой системы

/((/?)

по

передаточной функции

варьируемого элемента

(p),

определяемую

как

<n\

d\nK

(р)

п оч

Чувствительность

{p)

представляет собой отношение отно-

сительных изменений передаточной функции замкнутой системы

передаточной функции изменяемого элемента,

т. е.

—

~KW/

(p) '

V-

Очевидно,

что

чувствительностьSw

(p)

(7.3)

связана

функцией

чувствительности

(p)

(7.1)

соотношением

&b<P)-V$

(p)*$-.

(7.4)

Чем меньше чувствительность

(p) или

функция чувствитель-

ности

VwAp),

тем

меньше влияние передаточной функции

(p)

7 2]

0БЩ4Я

ФОРМУЛА

ЧУВСТВИТЕЛЬНОСТИ

рассматриваемого элемента на свойства автоматической систе-

мы.

Говоря об уменьшении или увеличении чувствительности,

мы всегда

будем

подразумевать уменьшение или увеличение ее

модуля. Естественно, что

чем

меньше

чувствительность

автоматической

системы,

тем

система

более

высококачественна.

Поэтому большой интерес представляют такие структуры авто-

матических

систем,

которые обладают малой чувствительностью.

7.2.

Общая

формула

чувствительности

Для вывода общей формулы чувствительности

{p),

выра-

жающей влияние изменения передаточной функции какого-либо

элемента

(p)

на передаточную функцию автоматической си-

стемы

К{р),

рассмотрим общий граф системы, в котором выде-

лена ветвь

соответствующая

варьируемому элементу (рис. 7.1).

Этот общий граф полностью оп-

ределяется:

ветвью сЪ, соответствующей

соединению элементов,

охваты-

вающих варьируемый элемент от-

рицательной обратной связью и

характеризуемых передаточной

Рис.

7.1.

функцией

Wi(p)\

ветвями

оЬ

ей,

соответствующими соединениям элементов

на

входе

и на выходе варьируемого элемента и характеризуе-

мыми

передаточными функциями

Wn(p)

Wm(p);

наконец,

ветвью

ad,

соответствующей соединениям элементов,

связывающих

вход

и выход системы при отсутствии варьируе-

мого элемента, т.е. при

(p)=

О, и характеризуемой переда-

точной функцией

Кс{р)-

Для краткости

будем

называть

Кс(р)

сквозной

передаточной

функцией,

Wn(p)

(p)~

входной

и соответственно

выходной

передаточными

функциями,

(p)Wi(p)

представляющую со-

бой передаточную функцию разомкнутого контура обратной свя-

зи,

—

контурной

передаточной

функцией.

Передаточная функция графа

К(р)

(рис. 7.2), очевидно,

равна

(п

\ —

к (п

\ .

^п

(Р)

Wui

(Р) ,

7К

(Р) -

(р) +

l + W6{p)Wl(p)

• (7.5)

Найдем вначале функцию чувствительности

(p).

По опре-

делению (7.1) имеем

ЧУВСТВИТЕЛЬНОСТЬ

АВТОМАТИЧЕСКИХ СИСТЕМ

[ГЛ.

Подставляя

{p)

(7.6) в

формулу

для

чувствительности (7.4),

получим

(7.7)

с*

(p)

\HJ—

(p)Wi(p)]

K{p)

Но

из

выражения передаточной функции

(7.5)

следует

(Р)

Win

(р)

(Р)

(р)

(7.8)

Поэтому окончательно общую формулу чувствительности

(7.7)

можно представить

виде

—

АР)

К(Р)

Рис

7.2

(7.9)

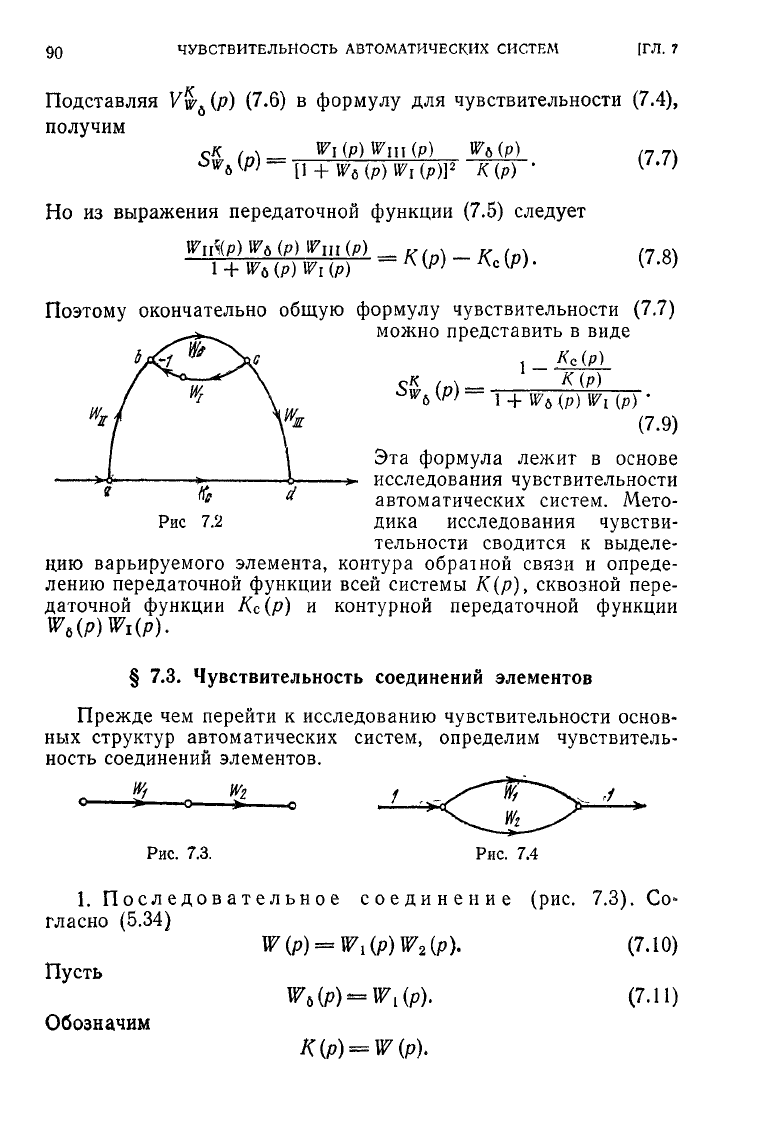
Эта формула лежит

основе

—>.

исследования чувствительности

автоматических систем. Мето-

дика исследования чувстви-

тельности сводится

выделе-

нию

варьируемого элемента, контура обратной связи

опреде-

лению передаточной функции всей системы

К(р)

сквозной пере-

даточной функции

Кс(р)

контурной передаточной функции

(p)W

(p).

7.3.

Чувствительность соединений элементов

Прежде

чем

перейти

исследованию чувствительности основ-

ных

структур

автоматических систем, определим чувствитель-

ность соединений элементов.

Рис.

7.3.

Рис.

7.4

Последовательное

соединение

(рис. 7.3).

Со-

гласно

(5.34)

W(p)~W

(p)W

{p).

(7.10)

Пусть

{p)^W

{

{pY

(7Л1)

Обозначим

7 3]

ЧУВСТВИТЕЛЬНОСТЬ

СОЕДИНЕНИЙ ЭЛЕМЕНТОВ

Для последовательного соединения

(Р)^О

lFi(p)-0.

(

7Л

Поэтому из общей формулы чувствительности (7.9) получаем

(p)

S^(p)

(7.13)

Чувствительность

последовательного

соединения

равна

единице.

2. Параллельное соединение (рис. 7.4). Согласно

(5.43)

W(p)

(p)

(p).

(7.14)

Пусть

W()

(p).

(7.16)

Обозначим

К(р)

W(p).

Для параллельного соединения

(рис.

7.4)

Kc(p)

(p),

!Ti(p)=iO.

(7.16)

Поэтому из общей формулы чувствительности (7.9) следует

или

Чувствительность

параллельного

соединения

равна

отно-

шению

передаточной

функции

варьируемого

элемента

передаточной

функции

соединения.

При

увеличении усиления неварьируемого элемента, т. е. эле-

мента, обладающего передаточной функцией

(p),

чувстви-

тельность параллельного соединения уменьшается, а при уве-

личении

усиления варьируемого элемента, т. е. элемента, обла-

дающего передаточной функ-

цией

Wi(p),

чувствительность

параллельного соединения уве-

личивается, стремясь к едини-

\^£

це.

Таким образом, в отличие

от последовательного соедине-

ис

' * *

ния,

при параллельном соеди-

нении

чувствительность может быть уменьшена за счет увеличе-

ния

усиления неварьируемого элемента.

3. Обратное соединение, или соединение

об-

ратной

связью (рис. 7.5). Согласно (5.54)

™

ос\Р)

_х_

W/.

(п\

Н7-

/гЛ

V'***'/