Цыпкин Я.З Основы теории автоматических систем
Подождите немного. Документ загружается.

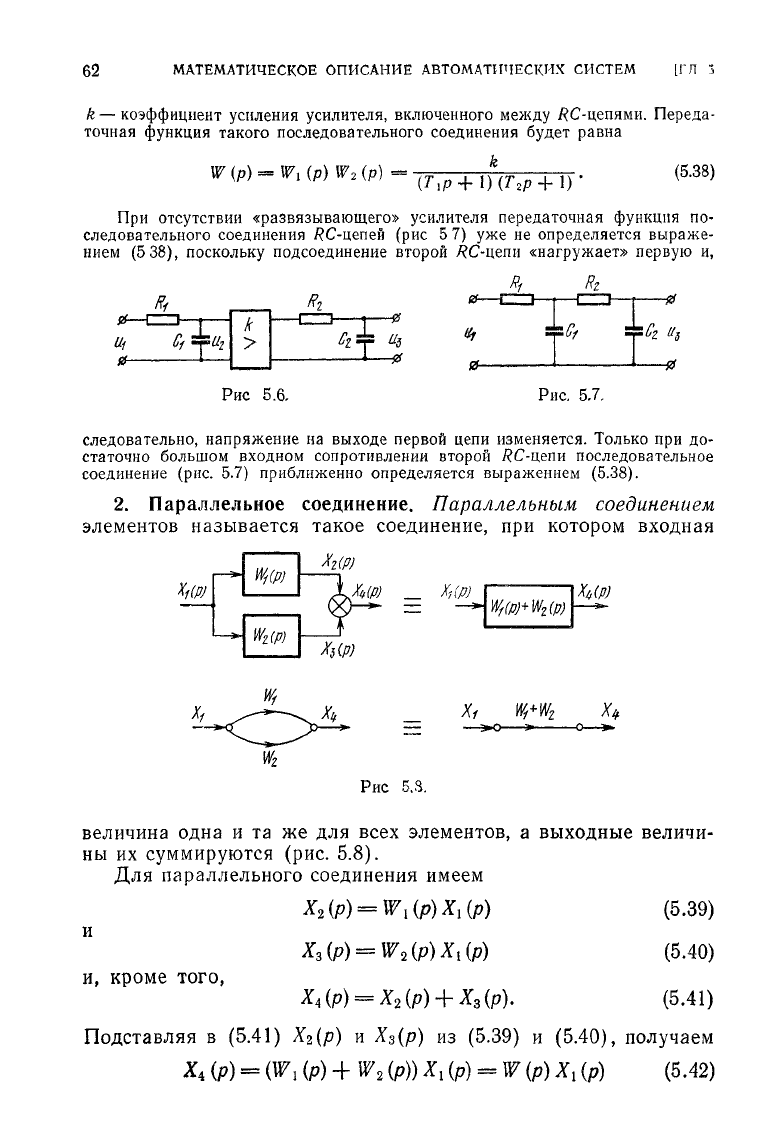
62
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ АВТОМАТИЧЕСКИХ СИСТЕМ
[ГЛ
3
k
— коэффициент усиления усилителя, включенного
между
/?С-цепями.
Переда-
точная функция такого последовательного соединения
будет
равна
W
(р)
=
W
x
(p)
W
2
(p)
(5.38)
При
отсутствии «развязывающего» усилителя передаточная функция по-
следовательного соединения
/?С-цепей
(рис 5 7) уже не определяется выраже-
нием
(5 38), поскольку подсоединение второй
/?С-цепи
«нагружает»
первую и,
Щ
Яг
(if
0-
Рис
5.6,
Рис,
5.7.
следовательно, напряжение на
выходе
первой цепи изменяется. Только при до-
статочно большом входном сопротивлении второй
RC-ixeun
последовательное
соединение (рис. 5.7) приближенно определяется выражением (5.38).
2. Параллельное соединение.
Параллельным
соединением
элементов называется такое соединение, при котором
входная
Щ(Р)
W
z
{p)
W
f
(p)+W
z
(p)
Рис
5,3.
величина
одна
и та же для
всех
элементов,
а
выходные
величи-
ны
их
суммируются
(рис. 5.8).
Для
параллельного
соединения
имеем
Р)
(5.39)
Р)
(5.40)
з(р).
(5.41)
и,
кроме того,
Подставляя в
(5.41)
Х%(р)
и
Х
3
(р)
из
(5.39)
и (5.40),
получаем
Xi
(р)
==
{W,
(р) +
W
2
(р))
X,
(р)
=
W (р)
X,
(р)
(5.42)
§5.3}
АЛГЕБРА
ПЕРЕДАТОЧНЫХ
ФУНКЦИЙ
и,
значит,
W(p)
=
W
l
{p)
+
W
2
(p).
(5.43)
В общем случае при параллельном соединении п элементов
W
(р) =
W
x
(р) +
W
2
(р) + ... +
W
n
(p). (5.44)
I
Передаточная
функция параллельного
соединения
равна
сумме
передаточных
функций
отдельных
звеньев.
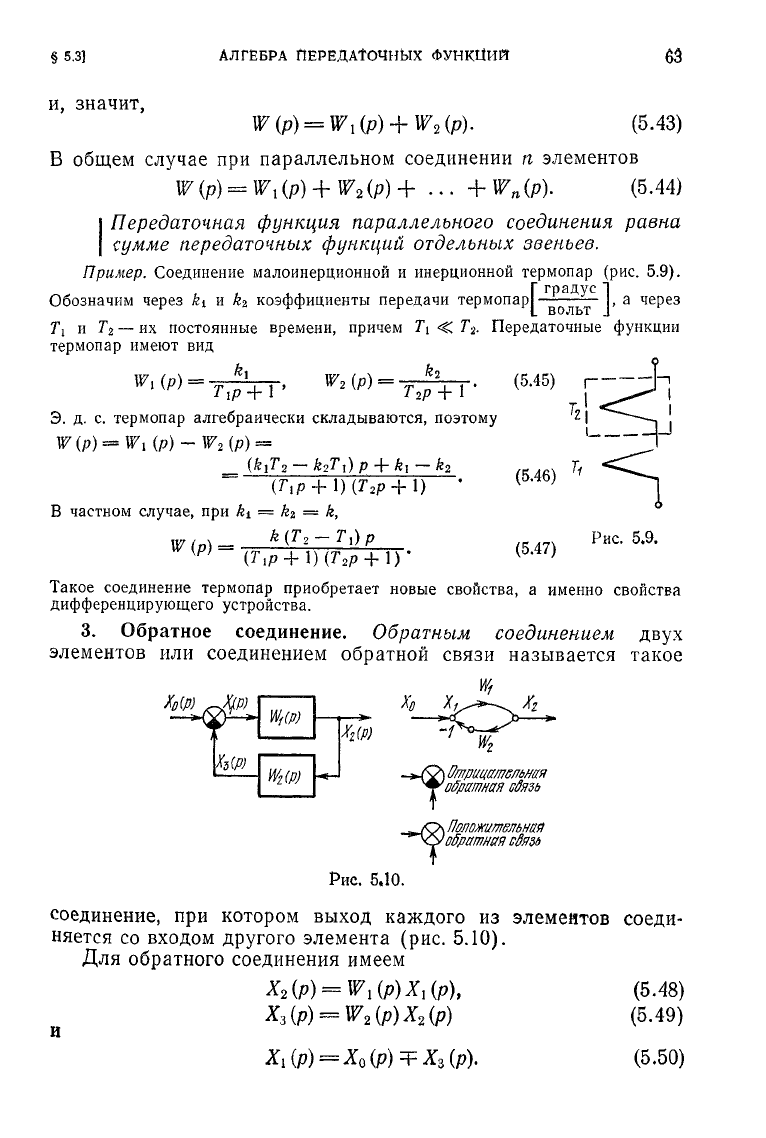
Пример.
Соединение малоинерционной и инерционной термопар (рис. 5.9).
[
градус 1
,
а через
ВОЛЬТ
J
Т\
и
Т
2
— их постоянные времени, причем
Т\
<
Т
2
.
Передаточные функции
термопар имеют вид
W
x
(p) =
•
(р)
••
Э.
д. с. термопар алгебраически складываются, поэтому
В частном случае, при
kt
=
й
2
=
k,
(5.45)
(5.46)
(5.47)
Рис.
5.9.
Такое соединение термопар приобретает новые свойства, а именно свойства
дифференцирующего устройства.
3.
Обратное
соединение.
Обратным
соединением
двух
элементов
или соединением обратной связи называется такое
Х
г
{р)
х
\
Положительная
у
обратная
сбязь
I
Рис.
5.10.
соединение,
при
котором
выход
каждого
из
элементов
соеди-
няется
со
входом
другого
элемента
(рис. 5.10).
Для
обратного
соединения
имеем
P),
(5.48)
P)
(5.49)
(5.50)

64
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ АВТОМАТИЧЕСКИХ СИСТЕМ [ГЛ.
5
Знак
минус в (5.50) соответствует отрицательной обратной свя-
зи,
а
знак
плюс — положительной обратной связи Из
уравнений
(5.48)
и (5.49), соответствующих последовательному
соедине-
нию
элементов,
следует
X
i
(p)
=
W
l
(p)W
2
{p)X(j)).
(5.51)
Заменяя
Х
3
(р)
в (5.50) его
значением
из (5.51), получим
*'^-i
±
wnP)
w
(б
-
52)
Подставляя
это
значение
в (5.48), будем иметь
Х
>
<Р)
=
1±^(РММР)
ХО
{р) = Гос {р) Хо {р)
•
(5
'
53)
Отсюда
находим передаточную
функцию
обратного
соединения:
^(р)=т±жйк(Д-
(5
-
54)
Элемент,
характеризуемый передаточной
функцией
Wi(p),
назо-
вем
прямой частью
замкнутой
системы,
а
элемент,
характери-
зуемый
передаточной
функцией
W
2
(p),—
обратной связью.
Передаточная функция обратного
соединения,
или соеди-
нения обратной связи, равна
дроби,
числитель которой
представляет
собой
передаточную функцию прямой части,
а знаменатель — передаточную функцию разомкнутой сис-
темы со знаком плюс, если обратная связь отрицательна,
или
со знаком
минус,
если обратная связь
положительна,
увеличенную на единицу.
Для
обратной
передаточной
функции
обратного
соединения
получаем
Woe
1
(p) =
WT
]
(p) ±
W
2
(p).
(5.55)
Обратная передаточная функция обратного соединения
равна алгебраической сумме обратной передаточной функ-
ции
прямой части и передаточной функции элемента об-
ратной связи.
Пример.
Рассмотрим
обратное
соединение
/?С-цепи
и
усилителя
(рис.
5 11).
Таким
образом осуществляется так
называемая
жесткая
обратная
связь.
Передаточные
функции
#С-цепи
и усилителя
равны
У
'
W
=
Тр+
1
'
T = RC (5>56)
и
W
2
(p)
-
k.
(5.57)

§
5 3]
АЛГЕБРА ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
Передаточная
функция обратного соединения равна
1
TF/
/*Л_
Т
Р
-\-\
__
1
7>
+ 1 ±
k
'
(5.58)
Тр+\
или, вводя обозначения эквивалентных коэффициентов усиления
и
постоянной
времени
l±k'
±k'
получаем
ос
(Р)
•
ТэкР
+
f
и
ь
*
(5.60)
к
-0
Введение жесткой обратной связи изменяет парамет-
ры
/?С-цепи.
При отрицательной обратной связи Рис 5.11.
(знак
+)
#эк
и
Гэк
уменьшаются в (1
-\-k)
раз.
При
положительной обратной связи
(знак
—)
к
вп
и
Г
эк
увеличиваются
в
(1 —k) раз при
k
< 1. Если же
k
=
1, то, как следует из (5.59),
(Р)
-
1
Тр
'
(5.61)
что соответствует интегратору. Из этого примера видно, что обратное соедине-
ние
позволяет качественно изменять свойства элементов.
При
преобразовании блок-схем или графов, помимо
указан-
ных выше правил определения передаточных функций
соедине-
ний,
полезно использовать правила переноса точки съема и точ-
ки
суммирования.
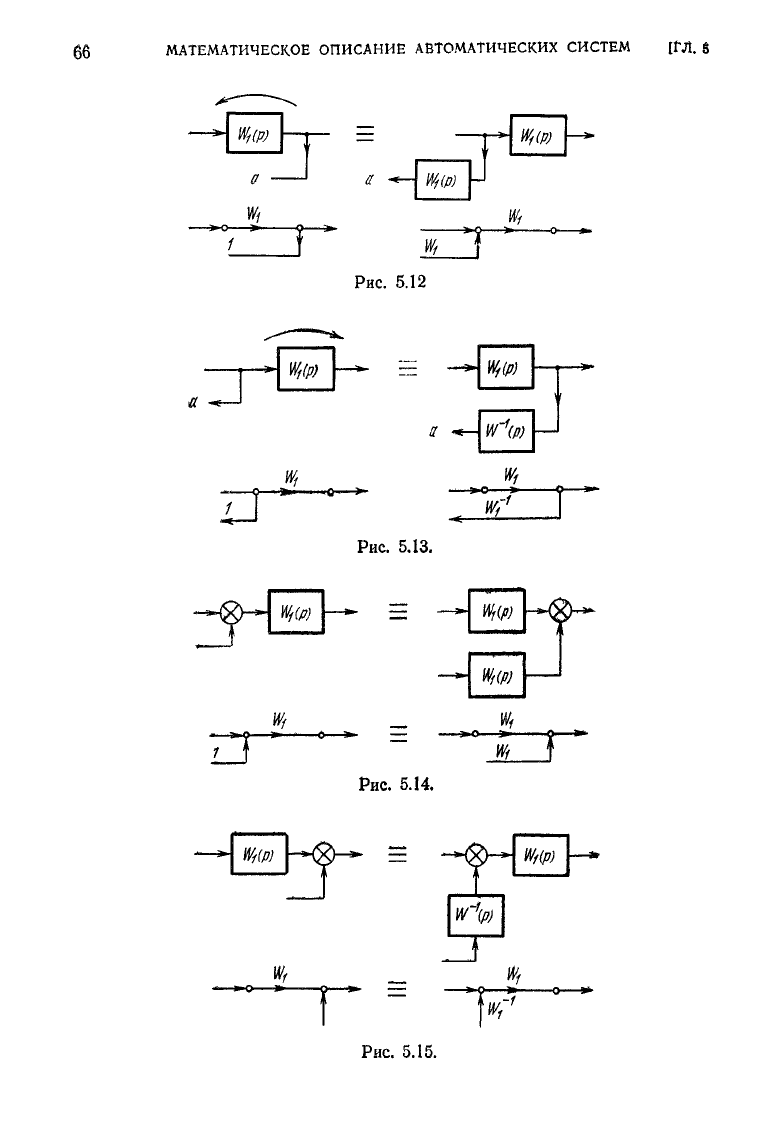
4. Правило переноса точки съема.
Если
точка
съема
переносится
против
направления
прохо-
ждения
сигнала,
то в
переносимую
ветвь
нужно
включить
элементы
с
передаточными
функциями
всех
элементов,
встречающихся
на пути
между
прежней
и
новой
точками
съема
(рис. 5.12).
Если
точка
съема
переносится
по
направлению
прохо-
ждения
сигнала,
то в
переносимую
ветвь
нужно
включить
элементы
с
обратными
передаточными
функциями
всех
элементов,
встречающихся
на пути
между
новой
и
преж-
ней
точками
съема
(рис.
5.13).
5. Правило переноса точки суммирования.
Если
точка
суммирования
переносится
по
направлению
прохождения
сигнала,
то в
переносимую
ветвь
нужно
включить
элементы
с
передаточными
функциями
всех
эле-
ментов,
встречающихся
на пути
между
прежней
и
новой
точками
суммирования
(рис.
5.14),
3 Я. 3.
Цыпкин
66
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ АВТОМАТИЧЕСКИХ СИСТЕМ
[ГЛ.
g

§
5 4]
ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ЗАМКНУТЫХ СИСТЕМ
67
Если
точка
суммирования
переносится
против
направления
прохождения
сигнала,
то в
переносимую
ветвь
нужно
вклю-
чить
элементы
с
передаточными
функциями
всех
элементов,
встречающихся
между
новой
и
прежней
точками
суммиро-
вания
(рис.
5.15).
§
5.4.
Передаточные
функции
и
уравнения
замкнутых
систем
Общая
методика определения передаточных функций
замкну-
тых систем состоит в следующем:
1. Переносим точки съема на основании правила 4 так, что-
бы образовались выделяемые последовательное, параллельное
соединения
и соединение с обратной связью.
2. Заменяем параллельно соединенные элементы и внутрен-
ние
обратные соединения на основании правил 1, 2, 3 эквива-
лентными
элементами.
3. Выписываем передаточную функцию замкнутой системы
на
основании правила 3 и по этой передаточной функции со-
ставляем уравнение замкнутой си-
стемы.
Рассмотрим в качестве примера
систему автоматического регулиро-
вания
числа оборотов электродвига-
теля. Поскольку в ней все типы со-
единений
(последовательное и об-
ратное) выделены, то нет необходи-
мости в первом этапе. Второй
Рис.
5.16=
этап
—
замена внутреннего обратно-
го соединения — сводится к введению вместо обратного соедине-
ния
эквивалентного элемента с передаточной функцией
W
ос
и
блок-схема примет более простой вид (рис.
5.16).
Прямая
часть системы включает элементы с передаточными функциями
W
oc
(p)
и
Wi(p),
а в обратную связь
входит
элемент с переда-
точной функцией
W
5
(p). Передаточная функция замкнутой си-
стемы
будет
равна
(p)
W
5
(p)
•
Vk.bd)
или,
в развернутой форме, после подстановки
W
oc
(p)
из (5.62),
г
(г
л
=
W*
(P)
W
2
(p)
1Г
3
(р)
W
A
(p)
W
1 +
W
2
(p)
W
b
(p)
W,
(p)
W,
(р) +
Wi
(p)
W
2
(p)
Wi
(p)
W,
(p)
W
6
(p)
•
(5.64)

68
МАТЕМАТИЧЕСКОЕ
ОПИСАНИЕ
АВТОМАТИЧЕСКИХ
СИСТЕМ
[ГЛ. 5
Уравнение замкнутой системы регулирования числа оборотов
двигателя, таким образом, представится в виде
N(p)
=
K
(p)
U
о
(р)-
(5.65)
В качестве
другого
примера, в котором необходимо использо-
вать все этапы методики определения передаточной функции,
Г(р)
Xf(p)
Х
7
(р)
Щ(Р)
Xz(P)
'Хъ(Р)
W
z
(p)
Рис.
5.17
рассмотрим блок-схему, изображенную на рис. 5.17. Соответ-
ствующий этой блок-схеме граф приведен на рис. 5.18, а. В от-
личие от предыдущего примера, все этапы
будем
проводить с
XQ
1
Xf
Wf
Xz
f
X$/S^*^Xfy
В)
Рис Б.13
помощью преобразований графа. Рис.
5.18,6
соответствует пере-
носу точки съема для образования выделяемого соединения вну-
тренней
обратной связи. Рис.
5.18,
в соответствует замене вну-
тренней
обратной связи эквивалентным элементом. Непосред-
ственно по преобразованному таким образом графу (рис.
5.18,
в)

и,
следовательно, уравнение
замкнутой
системы запишется в
виде
При
наличии несколь-
ких воздействий (рис.
5.19) на основании
прин-
ципа
суперпозиции нахо-
дятся передаточные
функ-
ции
замкнутой системы
относительно каждого
воздействия порознь. Затем они умножаются на изображение
соответствующих
воздействий и складываются. Так, для блок-
схемы рис. 5.19 передаточная функция по задающему воздей-
ствию
F
3
(p)
равна
Рис
5 19
Уравнение системы, следовательно,
будет
иметь вид
(5.70)
Рассмотрим общую блок-схему автоматической системы
(рис.
5.20).
Обозначим через
W
3
(p)
передаточную функцию со-
единения
элементов
между
точкой приложения задающего воз-
действия
/
3
(0
и выходной величиной
z(t),
а через
W
B
(p)~~
пере-
даточную функцию соединения элементов
между
точкой прило-
жения
возмущающего воздействия
f
B
(t)
и выходной величиной
2
(О*
Наконец, через
W(p)
будем
обозначать передаточную
выписываем передаточную функцию замкнутой системы:
§5 4] ПЕРЕДАТОЧНЫЕ
ФУНКЦИИ
ЗАМКНУТЫХ СИСТЕМ
69
(5.66)
(5.67)
(5.68)
(5.69)
а передаточная функция по возмущающему воздействию
F
B
(p)
равна
(5.71)
где
Подставляя
(5.67)
в (5.66), находим

70
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ АВТОМАТИЧЕСКИХ СИСТЕМ [ГЛ.
5
функцию
элемента
между
задающим
и
возмущающим воздей-
ствиями.
Тогда передаточные функции замкнутой системы
по за-
дающему
и
возмущающе-
\№
Zip)
W(p)
му
воздействиям будут
равны
соответственно
W
3
(P)
WAP)
(5.72)
Рис
5.20.
l
+
U7
B
(р)
И/(р)
•
(5.73)
Уравнение замкнутой системы относительно выходной величины
будет
иметь
вид
Z
(Р)
=
*
3
(Р)
F
a
(р)
+
К
в
(р)
F
B
(p). (5.74)
Изображение ошибки
Х(р)
связано
с
изображениями задающего
воздействия
F
3
(p)
и
выходной величины
Z(p)
простым соотно-
шением:
=
F
a
{p)-Z(p),
(5.75)
выражающим условие замыкания системы. Подставляя
в
(5.75)
Z(p)
из
(5.74), получим уравнение относительно ошибки:
X(р)
=
(1
—
/С.(р))
F
a
(Р)
-
^в
(Р)
F»
(Р).
(5.76)
При
наличии дополнительных воздействий, приложенных
к
различным точкам системы,
следует
определить соответствую-
щие передаточные функции
по
этим воздействиям
и
добавить
в
уравнение
(5.74)
слагаемые, равные произведению этих переда-
точных функций
на
изображения соответствующих воздействий.
Если
начальные значения
для
некоторых элементов отличны
от
нуля,
то их
можно рассматривать
как
дополнительные воздей-
ствия,
приложенные
ко
входу
этих элементов.
Так,
для
элемен-
тов, обладающих передаточными функциями вида (5.27),
изо-
бражения этих дополнительных воздействий определятся соглас-
но
(5.28)
как
Т /ЛЧ
(5.77)
(5.78)
что соответствует воздействию вида
б-функции
(см.
приложения
1 и 2).
Заметим,
что это
воздействие
x
H
(t)
су-
щественно
зависит
от
параметров элемента.
§5.4]
ПЕРЕДАТОЧНЫЕ
ФУНКЦИИ
ЗАМКНУТЫХ СИСТЕМ
7!
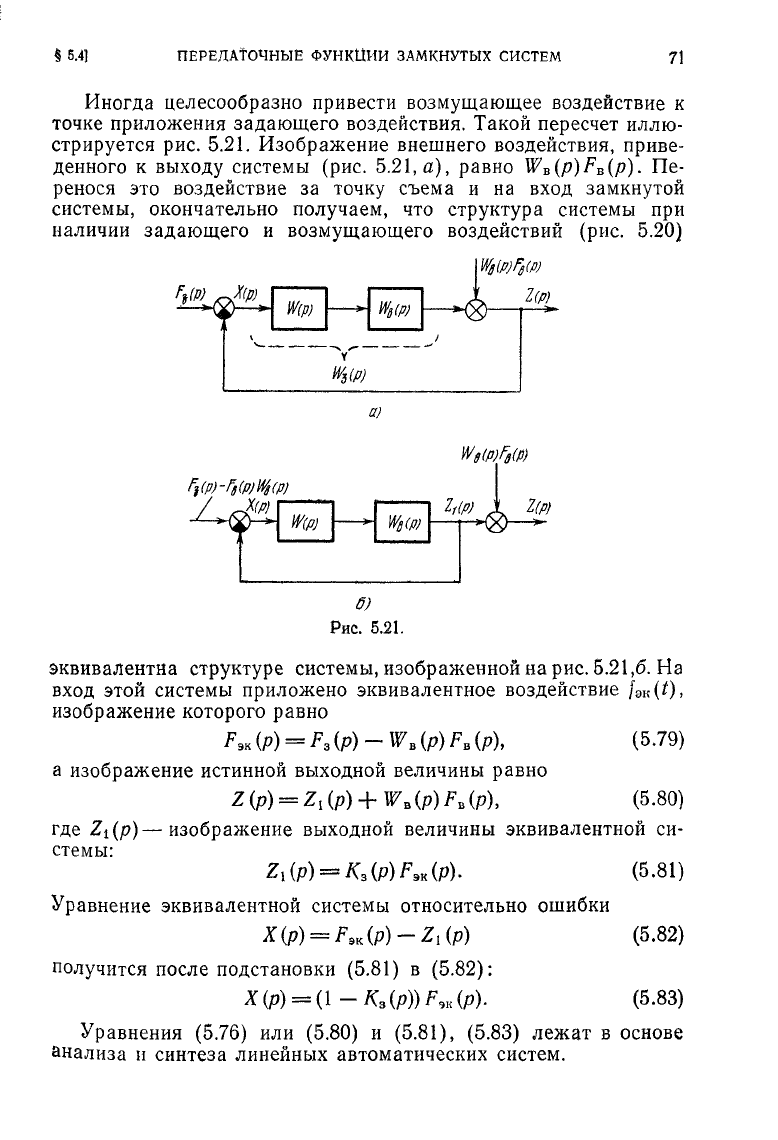
Иногда
целесообразно привести возмущающее воздействие
к
точке приложения задающего воздействия. Такой пересчет иллю-
стрируется
рис. 5.21.
Изображение внешнего воздействия, приве-
денного
к
выходу
системы
(рис.
5.21,
а),
равно
W
B
(p)F
B
(p).
Пе-
ренося
это
воздействие
за
точку съема
и на
вход
замкнутой
системы, окончательно получаем,
что
структура системы
при
наличии
задающего
и
возмущающего воздействий
(рис.
5.20)
-J(p)
V
"
*
Wip)
— ——"—
Щ(Р)
—""-— —-
Щ(Р)г
д
(Р)
А
1(р)
ю
1
W(p)
—*•
W
S
W
6)
Рис.
5.21.
эквивалентна
структуре системы, изображенной
на
рис.
5.21,6.
На
вход
этой системы приложено эквивалентное воздействие
/
Э
к(0»
изображение которого равно
/Чк
(Р)
=
F
3
(p)
-
W
B
(p)
F
B
(p),
(5.79)
а изображение истинной выходной величины равно
Z(p)
=
Z
l
(p)
+
W
B
(p)F
B
(p),
(5.80)
где
Zi(p)—изображение
выходной величины эквивалентной
си-
стемы:
ад)
=
/С
3
(р)^к(р).
(5.81)
Уравнение эквивалентной системы относительно ошибки
Xip)
=
Fn{p)-Z
x
{p)
(5.82)
получится после подстановки (5.81)
в
(5.82):
,
K
(p)-
(5.83)
Уравнения (5.76)
или
(5.80)
и
(5.81), (5.83) лежат
в
основе
анализа
и
синтеза линейных автоматических систем.
