Цыпкин Я.З Основы теории автоматических систем

Подождите немного. Документ загружается.

92 ЧУВСТВИТЕЛЬНОСТЬ АВТОМАТИЧЕСКИХ СИСТЕМ

[ГЛ. 7

где знак плюс соответствует отрицательной обратной связи, а

знак

минус соответствует положительной обратной связи.

Обо-

значим

)

(P)

(7.20)

положим вначале

Wi(p).

(7.21)

Это означает, что варьируется элемент в прямой части системы.

Поскольку

для обратного соединения

КЛР)**0,

{p)

{p),

(7.22)

то из общей формулы чувствительности (7.9) получаем

00 =

SS,

(P) =

l±Wl{

p)W2{p)

(7-23)

или,

учитывая (7.19),

о/С

(р)

Чувствительность

обратного

соединения

по

отношению

элементу

прямой

части

равна

отношению

передаточной

функции

соединения

передаточной

функции

варьируемо-

го

элемента

прямой

части.

Введение обратной связи изменяет чувствительность по срав-

нению

последовательным

соединением. Отрицательная обрат-

ная

связь (ей соответствует знак плюс в (7.23)) уменьшает чув-

ствительность соединения, а положительная обратная связь (ей

соответствует знак минус в (7.23)) увеличивает чувствитель-

ность.

При

увеличении

усиления

любого

из

элементов

соедине-

ния

отрицательной

обратной

связью

чувствительность

об-

ратного

соединения

по

элементу

прямой

части

умень-

шается.

Примем

теперь, что

(p)

(p),

(7.24)

что соответствует вариации элемента в обратной связи. Тогда

вместо (7.22) будем иметь

(р) =

(p),

}

(p) =

{

(p),

(7.25)

тогда из общей формулы чувствительности (7.9)

пол>чим

bWb\P)-*W

W—

(p)W

(p)

(p)/(ldbW

(p)WAP))

(7.26)

7.4]

ЧУВСТВИТЕЛЬНОСТЬ

ОСНОВНЫХ

СТРУКТУР

или,

после упрощений,

(

(p)W

(p)

{Р)

1 ±

(p)

Учитывая (7.19), представим

(p) в виде

S$Ap)

=FW

(p)W

(p).

(7.28)

Чувствительность

обратного

соединения

по

отношению

элементу

обратной

связи

равна

произведению

передаточ-

ных функций

соединения

варьируемого

элемента

(со

знаком

минус

для

отрицательной

обратной

связи

и знаком

плюс

для

положительной

обратной

связи).

Отрицательная обратная связь (ей соответствует

знак

плюс в

знаменателе (7.27)) уменьшает чувствительность обратного

со-

единения,.

а положительная обратная связь (ей соответствует

знак

минус в знаменателе (7.27)) увеличивает чувствительность

обратного соединения.

При

увеличении

усиления

любого

из

элементов

соедине-

ния с

отрицательной

обратной

связью

чувствительность

обратного

соединения

по

элементу

обратной

связи

увели-

чивается,

стремясь

единице.

Из

выражений чувствительностей

S^,

(р)

(7.23) и

SS^p)

(7.27)

следует, что

S^(p)-S^(p)

(7.29)

Разность

чувствительностей

обратного

соединения

по от-

ношению

элементам

прямой

части

обратной

связи

рав-

на

единице.

7.4. Чувствительность

основных

структур

автоматических систем

Как

правило, в автоматических системах варьируемым эле-

ментом является управляемый объект. Наряду с решением той

или

иной

задачи автоматического управления следует

умень-

шать чувствительность автоматической системы по отношению

возможным, непредвиденным изменениям параметров управ-

ляемого объекта Однако, помимо этого, нас

будет

интересовать

чувствительность автоматической системы к изменениям

управляющего устройства и других дополнительных корректи-

рующих

устройств.

ЧУВСТВИТЕЛЬНОСТЬ АВТОМАТИЧЕСКИХ СИСТЕМ [ГЛ. 7

Для определения чувствительности основных структур авто-

матических систем воспользуемся общей формулой чувствитель-

ности

(7.9):

KP)

1 +

(p)

•

частности,

при

/Cc(p)

(7.30)

из (7.9)

получаем

^W-i

wedmoo-

(

)

Если сквозная

передаточная

функция

равна

нулю,

то чув-

ствительность

автоматической

системы

полностью

опреде-

ляется

контурной

передаточной

функцией

(p)Wi(p).

Этот вывод существенно упрощает нахождение чувствитель-

ности

автоматической системы. Действительно, рассмотрим лю-

бую из типовых структур автомати-

ческих систем, приведенных в гл. 6.

7 Предположим, что в основной струк-

туре (рис.

7.6)

варьируемым эле-

ментом является управляемый объ-

ект. Тогда легко видеть, что для за-

Рис

дающего и возмущающего воздей-

ствий и выходной величины z сквоз-

ная

передаточная функция

(р)

равна нулю. Следовательно,

чувствительность

любой

типовой структуры по

отношению

управляемому

объекту

полностью

определяется

только

контурной

передаточной

функцией,

Введение дополнительных корректирующих элементов

(p),

W2u(p),

например, как это имеет место в разомкнуто-замкнутых

комбинированных системах, не влияет на чувствительность.

Введение же дополнительных элементов в замкнутый контур, на-

пример,

как это имеет место в основной структуре (рис. 7.7) и

системе с внутренней положительной обратной связью

(рис.

7.8), изменяет контурную передаточную функцию, а значит,

и чувствительность. Так, для основной структуры (рис. 7.7)

ЧУВСТВИТЕЛЬНОСТЬ

ОСНОВНЫХ

СТРУКТУР

для

системы

внутренней положительной обратной связью

(Р)

(р)

(p)

(р)

^у

(р)

ЪА\

(р) +

(p)

(p)'

Как

видно

из

приведенных выше выражений

для

чувствительно-

сти,

наличие обратной связи может понижать чувствительность

Рв

Рис.

7.7

Рис.

7.8

по

сравнению

разомкнутой системой,

для

которой

чувствитель-

ность равна единице. Сопоставляя выражение чувствительности

(7.32)

выражением передаточной функции ошибки

по

задаю-

щему воздействию (6.2), заключаем,

что для

обычной системы,

системы

внутренней положительной обратной связью

разо-

мкнуто-замкнутой системы

—/Св(р).

(7.35)

'об "об

Чувствительность

обычной

системы,

системы

внутренней

положительной

обратной

связью,

разомкнуто-замкнутой

системы

по

отношению

управляемому

объекту

равна

пе-

редаточной

функции

ошибки

по

задающему

воздействию.

Пользуясь общей формулой чувствительности (7.9), можно

определить чувствительность различных

структур

автоматиче*

ских систем

по

отношению

управляющему

корректирующим

устройствам. Рассмотрим

качестве примера наиболее общую

комбинированную разомкнуто-замкнутую систему, граф которой

изображен

на

рис.

7.9.

Передаточные функции

по

задающему

по

возмущающему воздействиям равны соответственно

(7.36)

Klip)

(p)

(р)

[1 +

(p)

(p)]

Wy{pjWo

(p)

~ •

(7>37)

Если

варьируемый элемент

не

входит

контур обратной связи,

как,

например, корректирующие элементы

(p)

W_K(JO),

TO,

ЧУВСТВИТЕЛЬНОСТЬ

АВТОМАТИЧЕСКИХ

СИСТЕМ

[ГЛ. 7

как

видно из рис. 7.2, в общей формуле чувствительности (7.9)

следует

положить

Wi(p)

0, и тогда

(7.38)

Поскольку

сквозные передаточные функции соответственно рав-

ны

(рис. 7.9)

•

(7.39)

1 +

(р)

то по формуле

(7.38)

получаем

>;/»=

(Р)

^2К

(Р)

У?*

(Р)

(p)

(7.40)

(7.41)

(7.42)

В этом случае чувствительность не зависит от управляемого объ-

екта. При увеличении усиления управляющего устройства

чув-

ствительность

(р)уменъ-

шается,

а чувствительность

(p) увеличивается,

стре-

мясь

к единице.

Чувствительность по

управляющему устройству

находится по общей форму-

ле (7.9). Принимая во вни-

мание,

что сквозные передаточные функции соответственно рав-

ны

(рис. 7.9)

(К1)

{р)

№

об

{р),

(7.44)

а контурная передаточная функция имеет вид

Wy(p)W

^(p)

по-

лучим по формуле (7.9)

cKl

™

^об

(Р)

(p)]

(р) +

(р)

(p)

(7.45)

(p)

(p)] [Wy (p) +

(p)]

(p) -

(p)\

(p)

(p)\

[\ +

(p)

(p)]

•

(7.46)

7.5]

СИСТЕМЫ НУЛЕВОЙ ЧУВСТВИТЕЛЬНОСТИ 97

При

И7

к(р)

= 0, что соответствует разомкнуто-замкнутой систе-

ме,

(р)

(7.46)

остается без изменений, а из

(7.45)

получаем

°w

yP>—

\ +

(p)W

(p)

Ht)

При

{p)

что соответствует комбинированной системе,

из

(7.45)

(7.46)

получаем

К°

(Р)

^об

(Р)

°^у

1Р]

^у

(Р)

(р) >

\Р)

— - 1 +

(р)

(р) • ^

Наконец,

при

(p)=

^2к(/?)^0,

что соответствует обычной

структуре

автоматической системы, чувствительности по отноше-

нию

к управляющему устройству определяются формулами

(7.48). При увеличении усиления управляющего устройства

к°

(p) уменьшается, стремясь к нулю, a

(p) увеличивается,

стремясь к единице.

7.5.

Системы нулевой чувствительности

Из

основной формулы чувствительности

^с

(Р)

оК

/ч

(р)

V(P)

можно установить два пути уменьшения чувствительности авто-

матических систем.

Первый

путь состоит в таком изменении передаточной функ-

ции

замкнутой системы

К(р),

при котором она приближалась бы

передаточной функции части системы, не зависящей от варьи-

руемого элемента. По

существу,

этот путь связан с

компен-

сацией

изменений варьируемого элемента, т. е. с измерением

эффекта,

вызываемого вариацией элемента, и созданием соот-

ветствующего компенсирующего воздействия. Классическим при-

мером реализации этого пути является известная мостиковая

схема компенсации. Этот путь, по

существу,

используется в разо-

мкнуто-замкнутой системе.

Второй путь состоит в увеличении усиления элементов кон-

тура

обратной связи. При стремлении усиления к бесконечности,

как

следует

из (7.32), (7.33), чувствительность по отношению

управляемому объекту

будет

стремиться к нулю. Поскольку

для обычной системы, системы с внутренней обратной связью и

комбинированной

системы чувствительность по отношению к

4 Я. 3. Цыпкин

98 ЧУВСТВИТЕЛЬНОСТЬ АВТОМАТИЧЕСКИХ СИСТЕМ

{ГЛ.

управляемому объекту равна передаточной функции

по

ошибке:

об "об

то системы

нулевой чувствительностью соответствуют системам

с нулевой ошибкой,

т. е.

инвариантным системам,

которых

шла

речь

в гл. 6.

обычной

комбинированной

системах

нулевая чувстви-

тельность

достигается

при

бесконечном

увеличении

коэф-

фициента

усиления

управляющего

устройства.

В системе

внутренней положительной обратной связью,

как

видно

из

(7.34)

или

условий инвариантности (6.34), нулевая

чув-

ствительность соответствует условию

(p)=W;

{p).

(7.49)

Система

внутренней

положительной

обратной

связью

об-

ладает

нулевой

чувствительностью

при

равенстве

переда-

точной

функции

элемента

обратной

связи

обратной

пере-

даточной

функции

охватываемого

управляющего

устрой-

ства, т.

е,

при

равенстве

произведения

этих

передаточных

функций

единице.

§"

7,6»

реализуемости систем нулевой чувствительности

Анализ формул чувствительности позволяет найти условия

нулевой чувствительности

для

любых структур автоматических

систем. Однако

мы

этим заниматься

не

будем, Дело

в том, что

системы нулевой чувствительности или,

что

эквивалентно, систе-

мы

нулевой ошибкой представляют собой идеальные системы,

если

бы

можно было

бы их

осуществить,

то

многие проблемы

теории автоматических систем были

бы

решены либо отпали

за

ненадобностью.

сожалению, однако,

на

пути осуществления

таких идеальных систем возникает множество препятствий

далеко

не все они

могут быть преодолены. Поэтому

эти

идеаль-

ные

системы могут служить лишь ориентиром,

которому

сле-

дует

стремиться настолько, насколько позволяют

нам

законы

природы

различного рода

ограничения,

которые вызваны огра-

ниченностью энергетических ресурсов, ограниченным диапазоном

изменений

величин, характеризующих состояние системы,

и т. д.

Условия нулевой чувствительности

нулевой ошибки требуют

неограниченного увеличения усиления элементов прямой части

системы, расположенных между точками приложения задающего

возмущающего воздействий. Удовлетворение этого требования

можно себе представить

как

непосредственное неограниченное

увеличение коэффициента усиления одного

из

элементов

(как в

7.6]

РЕАЛИЗУЕМОСТЬ СИСТЕМ НУЛЕВОЙ ЧУВСТВИТЕЛЬНОСТИ 99

обычной системе, см. § 6.1) либо, что физически эквивалентно,

как

создание контура внутренней положительной обратной связи

путем введения дополнительного элемента с передаточной функ-

цией

(p),

равной

(p)

(р) (как в системе с внутрен-

ней

положительной обратной связью, см. § 6.2). Действительно

при

этом условии, как видно из (6.16),

( \-

Wy{p)

вое

(Р)—

! _

WK {О)

Гу (р)

—

оо

Если

отвлечься от трудностей получения неограниченных уси-

лений

хотя бы по причине наличия ограничений на величину

управляющего воздействия, то при желании получить идеальные

системы мы сталкиваемся с невозможностью точной реализации

обратных передаточных функций

(7.49)

и с возникновением

неустойчивости по мере увеличения коэффициента усиления (см.

6.2) либо вариаций параметров. Эти обстоятельства не позво-

ляют осуществить идеальные системы нулевой чувствительности

или

нулевой ошибки. Условия нулевой чувствительности

требуют

введения в систему элемента, передаточная функция которого

(p)

равна обратной передаточной функции управляющего

устройства

Wy(p).

Аналогично этому, условия воспроизведения

(для разомкнуто-замкнутых систем, см. § 6.4) и условия компен-

сации

(для комбинированных систем, см. §

6.5)

требуют

введе-

ния

в систему корректирующих элементов, передаточные функ-

ции

которых равны обратной передаточной функции управляе-

мого объекта, т. е.

(p)

W$(p).

(7.50)

Так,

например, если

то согласно

(7.50)

получаем

Это значит, что корректирующий элемент, вводимый в систему,

помимо

безыскаженной передачи входного сигнала, должен осу-

ществлять идеально операции дифференцирования первого, вто-

рого и третьего порядков, что на практике точно осуществить

невозможно.

Условия типа

(7.50)

эквивалентны условию

100

ЧУВСТВИТЕЛЬНОСТЬ

АВТОМАТИЧЕСКИХ

СИСТЕМ

[ГЛ

(p)W

Q(p)=

которое означает,

что

от

вводимого

систему

элемента

передаточной функцией

(p)

требуется, чтобы,

бу-

дучи

последовательно соединенным

управляемым объектом,

обладающим передаточной функцией

e(p),

он

полностью

компенсировал

бы

инерционные свойства последнего. Невыпол-

нимость

этого требования особенно наглядно видна, если допу-

стить,

что

управляемый объект имеет запаздывание

реакции

выходной величины

на

входное

воздействие,

т. е.

(p)^k

e-P\

(7.53)

где

т—время

запаздывания.

этом

случае

вводимый

систему

элемент

или,

если угодно, управляющее устройство должно

об-

ладать передаточной функцией вида

(p)=±ei",

(7.54)

т.

е.

это

устройство должно быть наделено свойством предсказа-

ния,

упреждения,

что

физически невозможно. Поэтому условия

вида (7.49),

(7.50)

сколько-нибудь реальной ситуации точно

выполнить невозможно.

Таким

образом,

системы

нулевой

чувствительностью,

как и

инвариант-

ные

системы,

являются

идеальными

системами.

Идеальные системы

не

могут

быть физически реализованы,

задача обычно состоит

том,

чтобы реальные автоматические

системы приблизить, насколько

это

возможно,

идеальным

си-

стемам.

На

этом пути возникает много трудностей, таких,

как

наличие помех

элементах системы, дополнительные возмущаю-

щие

воздействия

и т. п.

Несмотря

на

невозможность реализации

идеальных систем,

мы им

уделили большое внимание потому,

что

они

указывают

нам

те

предельные возможности,

которым

следует

стремиться

при

создании автоматических систем

с уче-

том реальных условий.

Задачи

7.1.

Показать,

что

чувствительность передаточной функции

(п\

—

(p)

z(p)

л КР)

(р)

аЛ

(р)

по

параметру

равна

о/С,

(p)

a(A

(p)A

(p)-A

(p)A

(p))

°*

КР)

da К

(р) ""

Из

(р)

аЛ

(р))

{А,

(р)

аЛ

(р)) *

ЗАДАЧИ

101

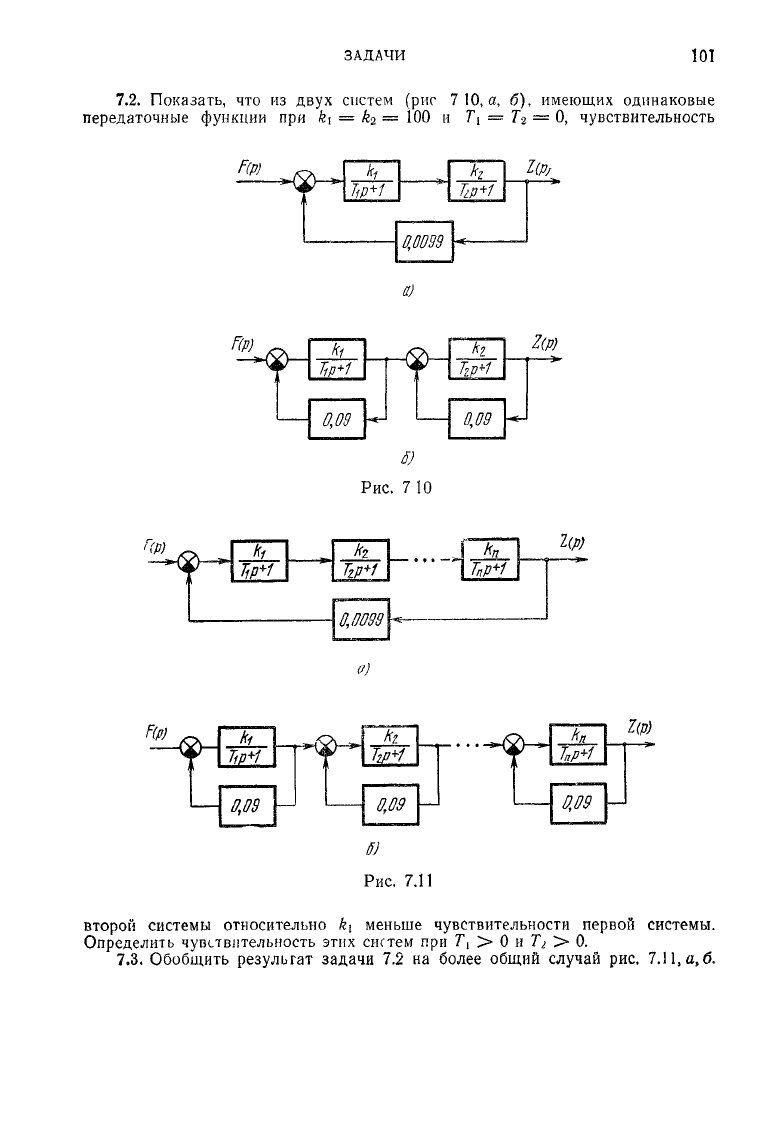
7.2. Показать, что из

двух

систем (рис 7

10,

а, б), имеющих одинаковые

передаточные функции при к\ =

100

= 0, чувствительность

Рис.

7 10

Рис.

7.11

Т1Р+1

0,0099

Tfp+f

0,09

L(P/

0,09

UP)

TiP

Tzp+1

0,0099

[MIL

-—Q

Tip+t

0,09

_/Os

p+1

0,09

TnP

второй системы относительно

к\

меньше чувствительности первой

системы.

Определить чувствительность этих систем при

{

>•

0 и

Тi

7.3. Обобщить

результат

задачи 7.2 на более общий случай рис.

7.11,

а,

б.