Цыпкин Я.З Основы теории автоматических систем

Подождите немного. Документ загружается.

522

ПРИЛОЖЕНИЯ

Одним из важнейших свойств преобразования Лапласа, кото-

рое способствовало широкому применению его для решения раз-

нообразных задач, является простота операций над изображе-

ниями

по сравнению с операциями над

оригиналами.

Так, дифференцированию и

интегрированию оригиналов соответ-

ствуют

более простые операции умноже-

ния

и деления на параметр преобразова-

ния

р в

случае

изображений. На основе

этих свойств и линейности преобразова-

ния

Лапласа от линейного дифференци-

ального уравнения относительно оригина-

лов переходят к линейному алгебраиче-

скому уравнению относительно изобра-

жений.

По найденному из этого уравне-

ния

изображению определяется оригинал

с помощью формулы обращения либо таблиц соответствий ори-

гиналов и изображений.

Пример.

Пусть / (t) =

Тогда из (1), (3) получаем

Рис.

П.1.

dt--

При

0, f (t)

1 (0, 0

/ <

оо

Важную роль при использовании преобразования Лапласа

играют теоремы, устанавливающие соответствия

между

опера-

циями

в области оригиналов и изображений. Приведем форму-

лировки

основных теорем с краткими указаниями способа их до-

казательства. Подробные доказательства и ряд дополнительных

теорем читатель может найти в книгах, приведенных в списке

литературы

Теорема

Линейность

преобразования

Лапласа:

(

' 1

«vfv

(t)

\ =

lv=l

)

v=l

(6)

Изображение

линейной

комбинации

оригиналов

равно

линейной

комбинации

их

изображений.

Теорема 2.

Дифференцирование

оригинала:

{f (/)} = pL {f (t)} - f

(0)

(p) - f (0), (7)

(/)}

- pf (0) - f

(0)

(p) - pf (0) - / (0) (8)

ПРЕОБРАЗОВАНИЯ

ЛАПЛАСА И

ФУРЬЕ

52$

и,

в общем случае,

{f(t)} - t

p»-

(0) =

(p)

(0), (9)

()

Равенство

(7)

находится интегрированием основного

соотно-

шения

(1) по

частям. Равенство

(9)

получается

последователь-

ным

применением

(7) к

соотношению

}

Если

f(*-D(O)

ft =

l,2,

....

то

из (9)

получаем

{/<">

(/)}

P"L

(0)

(p).

(10)

этом случае

п-кратному

дифференцированию оригинала со-

ответствует

умножение изображения на

Теорема

3. Интегрирование оригинала:

(11)

Интегрированию

оригинала от 0 до t

соответствует

деление

изо-

бражения на р.

Соотношение

(11)

можно получить, например, интегрирова-

нием

(1) по

частям.

Теорема

4. Смещение аргумента оригинала (теорема

за-

паздывания)

L{f(i-

т)}

e-P-L

(/)} =

e-P*F

(p).

(12)

Предполагается,

что f(t —

т)=

0 при t

т.

Смещению

аргумен-

та оригинала на т соответствует

умножение

изображения

на

е~

рх

Соотношение

(12)

вытекает

из (1) при

замене

в нем f(t) на

f(t

—

т) и

последующей замене переменной

t на t

-f-1.

Теорема

5. Смещение аргумента изображения:

F(p +

L{e-**f(t)}.

(13)

Смещению аргумента изображения на а

соответствует

умноже-

ние

оригинала на

Теорема

6. Умножение изображений (теорема свертыва-

ния):

(14)

524

ПРИЛОЖЕНИЯ

Операция

называется сверткой.

Изображение

свертки двух

оригиналов

равно

произведению

их

изображений.

Равенство

(14)

можно получить умножением обеих частей

(1)

на

F2(p)

применением теоремы

Теорема

Площадь

оригинала:

f(t)dt.

(15)

Площадь

оригинала

(если

она

существует)

равна

начальному

значению

изображения.

Соотношение

(15)

следует

из

(1)

при

р = 0.

е о р е

а 8.

Предельные

значения:

\impF{p)=limf(t)

f(O),

(16)

f(oo),

(17)

эта

предельные

значения

существуют.

Эта теорема позволяет найти значение оригинала

при t = 0

оо

по

изображению. Соотношения

(16) и (17)

следуют

из

(7) при стремлении

р к

бесконечности

нулю.

Наиболее часто встречающиеся оригиналы

соответствую-

щие

им

изображения приведены

табл. П.1.

Наряду

односторонним преобразованием Лапласа, опреде-

ляемым формулами

(1) и (4),

иногда вводят

рассмотрение

двустороннее преобразование Лапласа

(18)

(19)

—

/СО

котором оригинал

(f)

определен

интервале

—оо

< t <

оо.

Для двустороннего преобразования Лапласа справедливы теоре-

мы

1, 4, 5.

Что

же

касается теорем

2, 3, 6, 7, то их

формулировки

несколько

упрощаются благодаря тому,

что f(t)

определено при

всех значениях

поэтому начальные значения оригналов

ПРЕОБРАЗОВАНИЯ

ЛАПЛАСА

ФУРЬЕ

Таблица

П.1

1(0

/n\

sin

cat

cosco^

sin

(<at

— ф)

sin {cat — ф)

F(p)=L{/(^)}

—

се

со

cos

— p sin

cos

— (p — a) sin

(p -

+ со

производных

в них не

фигурируют. Если

в (18)

предположить,

что

/(0^=0

при

/<0,

(20)

то

двустороннее

преобразование Лапласа превращается

одно-

стороннее.

Полагая

двустороннем преобразовании Лапласа

(18) и (19)

/со,

мы

приходим

преобразованию

Фурье:

или,

кратко,

со

или,

кратко,

(/)

gr~

(/со)}.

(21)

(22)

(23)

(24)

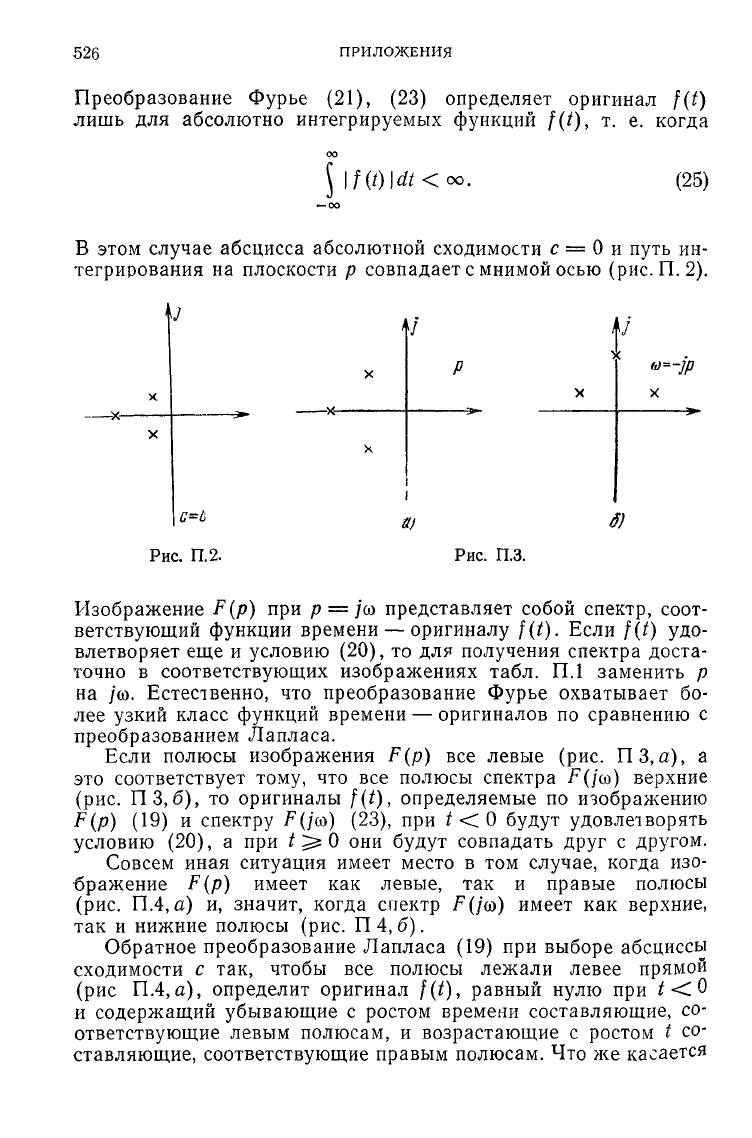
526

ПРИЛОЖЕНИЯ

Преобразование Фурье (21), (23) определяет оригинал f(t)

лишь

для абсолютно интегрируемых функций

/(/),

т. е. когда

оо.

(25)

В этом

случае

абсцисса абсолютной сходимости с = 0 и путь ин-

тегрирования на плоскости р совпадает с мнимой осью (рис. П. 2).

в)

Рис.

П.

Рис. П.З.

Изображение

F(p) при р = /со представляет собой спектр, соот-

ветствующий функции

времени

— оригиналу f(t). Если

f(t)

удо-

влетворяет еще и условию (20), то для получения спектра доста-

точно в соответствующих изображениях табл. П.1 заменить р

на

/со. Естественно, что преобразование Фурье охватывает бо-

лее узкий класс функций времени — оригиналов по сравнению с

преобразованием Лапласа.

Если

полюсы изображения

F(p)

все левые (рис. П 3, a), a

это

соответствует

тому,

что все полюсы спектра

F(/со)

верхние

(рис.

П 3, б), то оригиналы

f(t),

определяемые по изображению

F(p) (19) и спектру

F(/<D)

(23), при

£<0

будут

удовлетворять

условию (20), а при t ^ 0 они

будут

совпадать

друг

с другом.

Совсем иная ситуация имеет место в том случае, когда изо-

бражение F(p) имеет как левые, так и правые полюсы

(рис.

П.4, а) и, значит, когда спектр

F(jay)

имеет как верхние,

так

и нижние полюсы (рис.

ПА,

б).

Обратное преобразование Лапласа (19) при выборе абсциссы

сходимости с так, чтобы все полюсы лежали левее прямой

(рис

П.4,а),

определит оригинал

f(t),

равный нулю при

t<.0

содержащий убывающие с ростом времени составляющие, со-

ответствующие левым полюсам, и возрастающие с ростом t со-

ставляющие, соответствующие правым полюсам. Что же касается

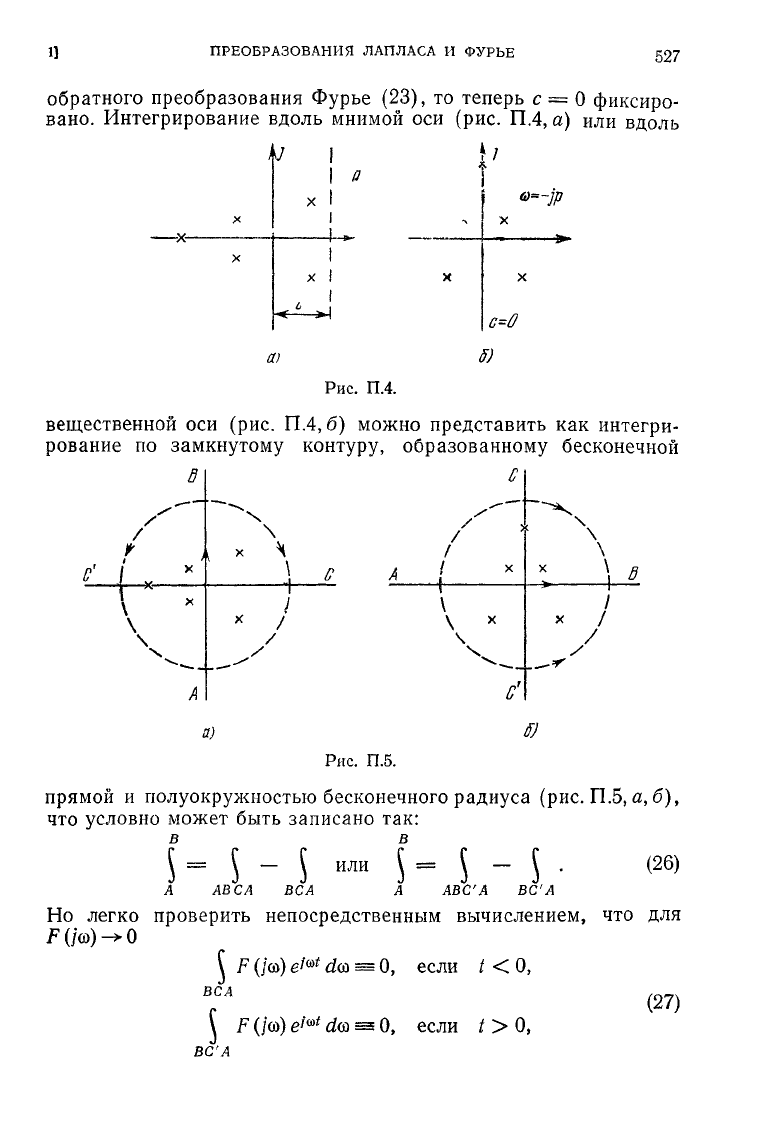
ПРЕОБРАЗОВАНИЯ

ЛАПЛАСА

И ФУРЬЕ

527

обратного преобразования Фурье (23), то теперь с = О фиксиро-

вано.

Интегрирование вдоль мнимой оси (рис.

ПА,

а) или вдоль

;

с=0

Рис.

П.4.

вещественной оси (рис.

П.4,

б) можно представить как интегри-

рование по замкнутому контуру, образованному бесконечной

В С

й)

Рис.

П.5.

прямой

и полуокружностью бесконечного радиуса (рис.

П.5,

а,

б),

что условно может быть записано так:

в в

iii

/ОА\

\ —

или

\ = \ — \ .

\ло)

АВС

ВС

А А

АВС

ВС

Но

легко проверить непосредственным вычислением, что для

(/©)-»

F (/со)

е№

Ас

= 0, если / < О,

ВСА

(/©)

0, если

> О,

(27)

вел

528

ПРИЛОЖЕНИЯ

что интеграл по контуру

АВС'А,

охватывающему левую (верх-

нюю)

полуплоскость, определяет f(t) при t > 0, а интеграл по

контуру

АВСА,

охватывающему правую (нижнюю) полупло-

скость,

определяет f(t) при t < 0. Таким образом, если разло-

жить

F(/o))

на простейшие дроби, то составляющие, соответ-

ствующие верхним полюсам, определят

fk(t)

при t

0, а со-

ставляющие,

соответствующие нижним полюсам, определят

fk(t)

при

t < 0.

Пример.

Пусть

F (р)

- а) (р +

—

alp

-\-Ь

Тогда оригинал, соответствующий обратному преобразованию Лапласа,

будет

равен

/(О

о,

*<o

(28)

/«

b — a

Применим

теперь обратное преобразование Фурье

t > 0.

F (/©)

этом

случае

(/со — а)

(/(0

+ Ь)

Ь — a L /со —

у© —

fit)'

b — а

b — a

~bt

t<0,

t>0.

(29)

Полученные оригиналы изображены на рис. П.6, а и б соответственно. Они

существенно отличаются

друг

от

друга.

Очевидно, что оригинал

f(t)

а)

Рис.

П.6.

рис.

П.6, б

соответствует

физически нереализуемому процессу, так как он

существует

при отрицательном времени.

ИМПУЛЬСИВНЫЕ

ФУНКЦИИ

529

2. Импульсивные функции

Для выяснения смысла импульсивной функции, или, как ее

еще называют, б-функции, рассмотрим разрывную функцию вида

скачка (рис. П.7). Эта функция аналитически представима в

I(/)=-l(l

sign/),

(30)

где

{

при / > 0, _____

О при /==0, (31)

—

при t < 0.

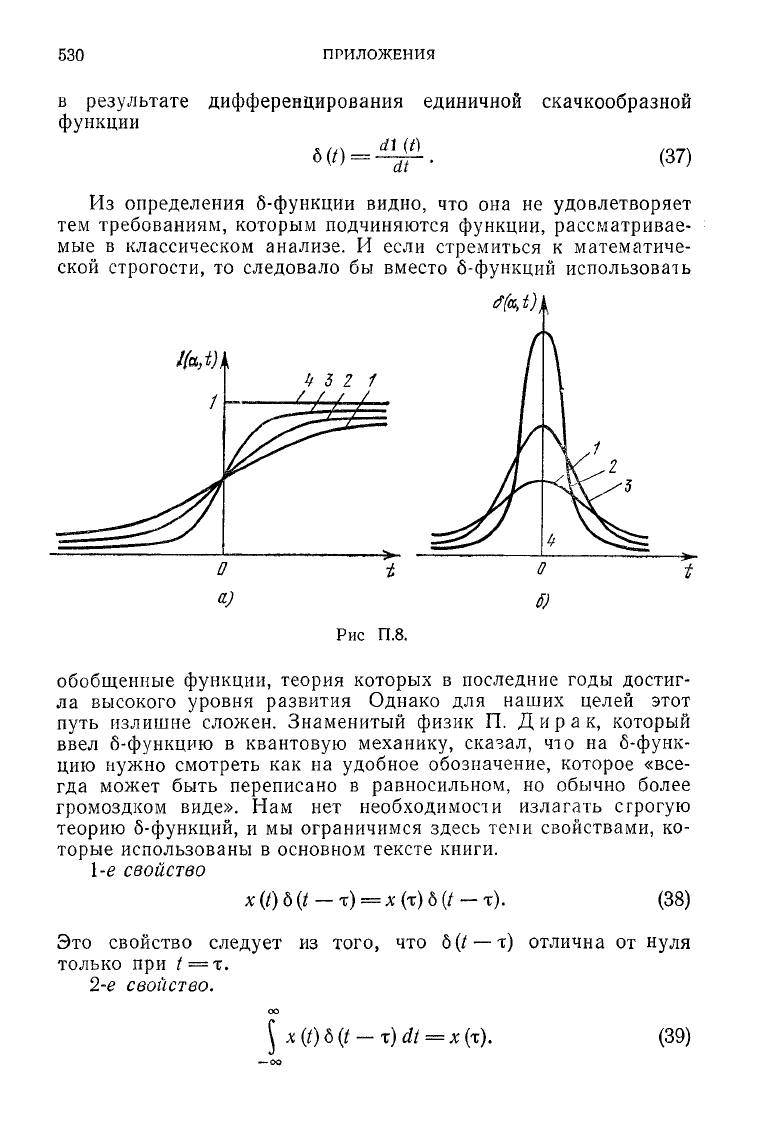
Разрывную функцию 1 (t) можно

р П7

рассматривать как предел

неко-

ис

' '

горого семейства непрерывных

функций при изменении параметра этого семейства, например:

1 1

I (a, t) =

—

arctg

а/. (32)

В пределе

при

а-*оо,

как

видно

из

рис.

П.8,

а,

lim

(а,

(/).

(33)

Обозначим

производную 1 (а,

через

(а,

/),

так что с учетом (32)

б (a, t) =

—^-^-

—rz~W'

@4)

Площадь

(a,

(рис.

П.8,

б) не зависит от а и всегда равна 1:

оо

б (а,

[б (а,

01Г»

[т

]

(

)

—

оо

Возможны

иные, более сложные семейства, обладающие свой-

ствами

(33), (35).

Определим

импульсивную функцию, или 6-функцию, как

предел б (а,

при

оо,

т. е.

б(/)=

lim

(а,

/).

(36)

а->оо

8-функция

представляет

собой

функцию,

равную нулю во всех

точках,

кроме точки t = 0, причем

«площадь»

этой 8-функции

равна единице. Физически б-функцию можно представить себе

как

ток, протекающий через емкость, включенную на постоянное

напряжение

в 1 В. Формально б-функция может быть получена

18 Я. 3

Цыпкин

530

ПРИЛОЖЕНИЯ

результате

дифференцирования единичной скачкообразной

функции

Из

определения б-функции видно, что она не удовлетворяет

тем требованиям, которым подчиняются функции, рассматривае-

мые в классическом анализе. И если стремиться к математиче-

ской

строгости, то следовало бы вместо 6-функций использовать

5 2 1

а)

Рис

П.8.

обобщенные функции, теория которых в последние годы достиг-

ла высокого уровня развития Однако для наших целей этот

путь излишне сложен. Знаменитый

физик

П.

Дирак,

который

ввел

6-функцию

в квантовую механику, сказал, что на б-функ-

цию

нужно смотреть как на удобное обозначение, которое

«все-

гда может быть переписано в равносильном, но обычно более

громоздком виде». Нам нет необходимости излагать

строгую

теорию б-функций, и мы ограничимся здесь теми свойствами, ко-

торые использованы в основном тексте книги.

1-е

свойство

x{t)6{t

— т)

—т).

(38)

Это свойство следует

из

того,

что

(/—-г)

отлична

от

нуля

только

при

т.

2-е

свойство.

(39)

ИМПУЛЬСИВНЫЙ

ФУНКЦИИ

531

Это свойство вытекает из 1-го свойства. Действительно,

оо

—

)

(х)

— т) dt =

А;

(Т)

—

оо

Но

из определения б-функции

следует,

что

(40)

Заметим,

что бесконечные пределы в (39) можно заменить ко-

нечными,

но так, чтобы аргумент б-функции обращался в нуль

внутри этих пределов:

х (t)

&(l—x)dt

x{t)b{t—x)dt=x{x)

г—е

(41)

3-е

свойство.

где /

— нули функции

x(t),

т. е. корни уравнения

x(t)

которые предполагаются простыми. Суммирование

(42) ведется по всем корням /

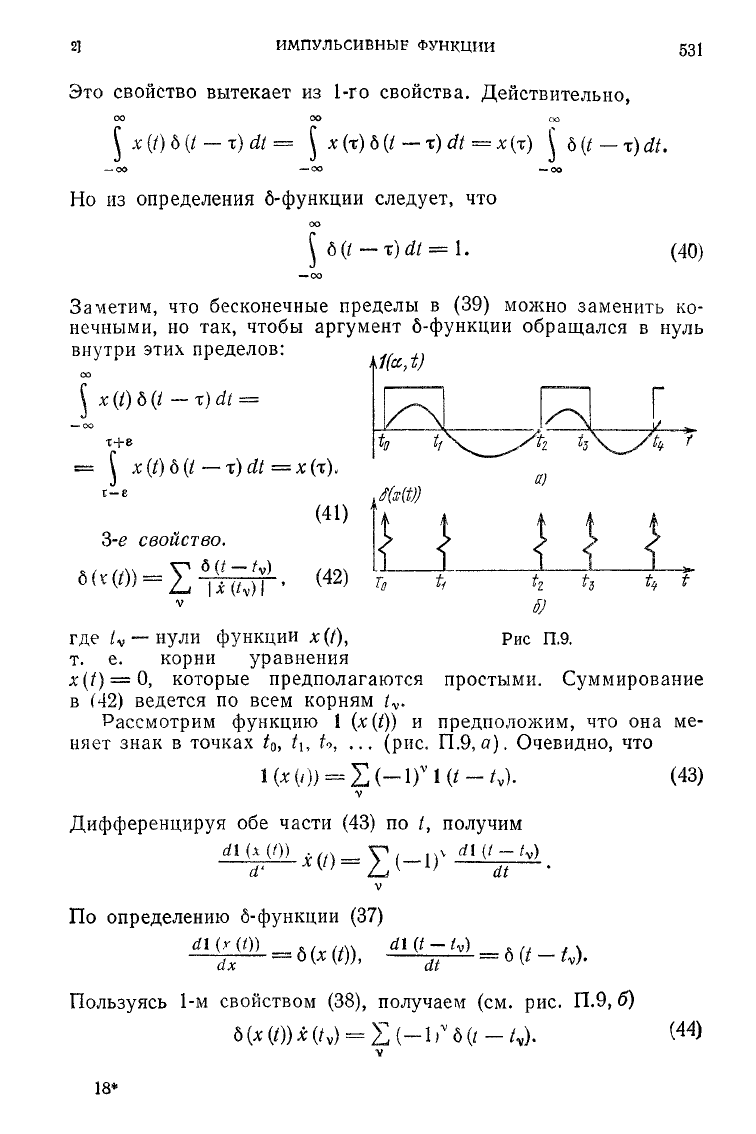
Рассмотрим функцию 1 {x(t)) и предположим, что она ме-

няет

знак в точках

, t

to,

... (рис.

П.9

а),

Очевидно, что

(*('))

E(-l)

l(*-*v).

(43)

Дифференцируя

обе части (43) по /, получим

По

определению б-функции (37)

dl {t

Пользуясь 1-м свойством (38), получаем (см. рис,

П.9,

б)

(х (/))

)

Z(—b

6(/—

18*