Цыпкин Я.З Основы теории автоматических систем

Подождите немного. Документ загружается.

482

УСТОЙЧИВОСТЬ

НЕЛИНЕЙНЫХ

ИМПУЛЬСНЫХ

СИСТЕМ

[ГЛ. 35

Процессы

нелинейной

импульсной

системе

устойчивой

импульсной

частью,

вызываемые

ограниченным

внешним

воздействием,

будут

устойчивыми,

если

коэффициент

диф-

ференциальной

линеаризации

нелинейного

элемента

удо-

влетворяет

условию

few(*)<£<,,

(35.53)

частотная

характеристика

линейной

импульсной

части

W*(j(d)

расположена

справа

от

вертикальной

прямой

—

-у>

где k > fe

Условие (35.53), налагаемое на коэффициент дифференциаль-

ной

линеаризации

&СЮ(#),

равносильно не только условию принад-

лежности характеристики нели-

нейного элемента сектору

(0,fe),

но

и ее монотонности (рис. 35.4).

Критерий абсолютной устойчиво-

сти процессов предъявляет более

жесткие требования к характери-

стике нелинейного элемента, чем

критерий абсолютной устойчиво-

сти состояния равновесия.

Если характеристика нелиней-

ного элемента зависит от вре-

мени:

Рис.

35.4.

Ф(х,

т),

то и коэффициенты статической линеаризации

(35.54)

дифференциальной

линеаризации

йФ

(*е,

т)

(35.55)

будут

также зависеть от времени

т.

Критерии абсолютной устой-

чивости состояния равновесия и процессов такой нестационарной

системы формулируются, как и выше, но вместо

стационарны^

коэффициентов

статической и дифференциальной линеаризации

в них фигурируют нестационарные коэффициенты статической и

дифференциальной линеаризации и условия вида (35.49),

(35.53)

должны выполняться при всех значениях т.

35.4]

ОБЩИЙ

КРИТЕРИЙ

АБСОЛЮТНОЙ УСТОЙЧИВОСТИ

35.4. Общий критерий абсолютной устойчивости

483

Рассмотрим теперь нелинейную импульсную систему,

кото-

рой линейная импульсная часть может быть нейтральной

или

неустойчивой,

но при

этом такой, которая допускает стабилиза-

цию

при

помощи пропорциональной обратной связи

(рис.

35.1).

Эквивалентными преобразованиями

эту

структурную

схему

легко привести

виду

как на рис. 35.5, где г

—постоянная

Рис

35.5

величина.

этой схеме характеристика нелинейного элемента

определяется

как

(х)

Ф(х)-гх,

(35.56)

Частотная характеристика линейной импульсной части равна

(/©)

(35.57)

(/со)

а спектр внешнего воздействия определяется выражением

ffi}

(35.58)

Из

(35.56)

следует,

что

коэффициенты статической

дифферен-

циальной линеаризации характеристики преобразованного

Фп(#)

исходного

Ф(х)

нелинейных элементов связаны соотноше-

ниями

{

^(x)

{c)

(x)-r

(35.59)

(д) / \

^д)

/ \

/о

г*

г\\

(х)

—

г.

(35.60)

Если коэффициенты статической

дифференциальной линеари-

зации

нелинейного элемента удовлетворяют неравенствам

й<д>

(х)

(35.61)

(35.62)

16*

484

УСТОЙЧИВОСТЬ

НЕЛИНЕЙНЫХ

ИМПУЛЬСНЫХ

СИСТЕМ

[ГЛ. 35

то согласно

(35.59),

(35.60)

}

{x) и

k^ix)

неравенствам

0 <

£п

с)

(х)

-r

0 <

{

]

(х)<

г.

будут

удовлетворять

(35.63)

(35.64)

Поскольку

приведенная линейная импульсная часть должна

быть устойчива, то согласно частотному критерию устойчивости

(

—-г-,

/01

положительном направлении

sJ2

раз, где

— индекс неустой-

чивости исходной линейной части. Условие неотрицательности

типа

(35.47)

запишется в виде

(/©) +

-г-!—

(35.65)

«о —

Подставляя в

(35.65)

значение

(/со) из (35.57), получим после

простых преобразований

>r).

(35.66)

Граница области, определяемой неравенством (35.66), задается

уравнением

14 с

+ rW* (/со)

или,

что равносильно,

Re [1 +

(/©)]

rW*

/со)] - 0.

(35.67)

Уравнение вида

(35.67)

определяет собой окружность, про-

Jr%

ходящую через точки

— —

---г-

с центром на оси

(

абсцисс в точке —

-х-

[

—Ь

т~

радиусом

-й-

б)

а об-

Рис.

35.6.

ласть, определяемая

неравен-

ством (35.66), соответствует

внешности

окружности при

> 0 (рис. 35.6, а) и внутренности при

< 0 (рис.

35.6,6).

Назовем

для краткости эти окружности

r) -окружностями.

Неравенство

(35.66)

будет

выполняться, если частотная харак-

теристика линейной импульсной части

будет

находиться в неза-

штрихованной области. Теперь нетрудно сформулировать кру-

говые

критерии

абсолютной

устойчивости.

§35

ОБЩИЙ

КРИТЕРИЙ

АБСОЛЮТНОЙ

УСТОЙЧИВОСТИ

485

Критерий

абсолютной

устойчивости

состояния

равнове-

сия (круговой

критерий).

Состояние равновесия нелиней-

ной импульсной системы будет абсолютно

устойчивым,

если коэффициент

статической

линеаризации нелинейного

элемента удовлетворяет неравенству

r<№(x)<k

(35.68)

частотная

характеристика

линейной импульсной части

W*(jcb)

при 0

<(о<;-у-

охватывает

(ko

r)-окружность

при k <

> 0 против часовой стрелки

раз,

где

— индекс

неустойчивости.

На

рис. 35.7

изображены

случаи

абсолютной

устойчивости

состояния

равновесия

при

= 0 (а) и

= 2 (б).

Условие

(35.68),

налагаемое

на

коэффициент

статической

линеаризации

Рис.

35.7.

равносильно

условию

принадлежности

характеристики

нелинейного

элемента

Ф(х) углу

(г,

)

(рис.

35.8).

Критерий абсолютной устойчивости процессов (круговой

критерий).

Процессы в нелинейной импульсной

системе,

вызванные ограниченным внешним воздействием, будут

аб-

солютно устойчивыми, если

коэффициент

дифференциаль-

ной линеаризации нелинейного элемента

удовлетворяв!

условию

№

(х) <

(35.69)

частотная

характеристика

линейной импульсной части

(/со) при 0

со

-«г-

охватывает

(ko,

-окружность

при k <

> 0 против часовой стрелки

раз,

гда

— индекс

неустойчивости.

Условие

(35 69),

налагаемое

на

коэффициент

дифференциаль-

ной

линеаризации

при

> 0,

равносильно

условию

монотонности

486

УСТОЙЧИВОСТЬ

НЕЛИНЕЙНЫХ

ИМПУЛЬСНЫХ

СИСТЕМ

[ГЛ. 35

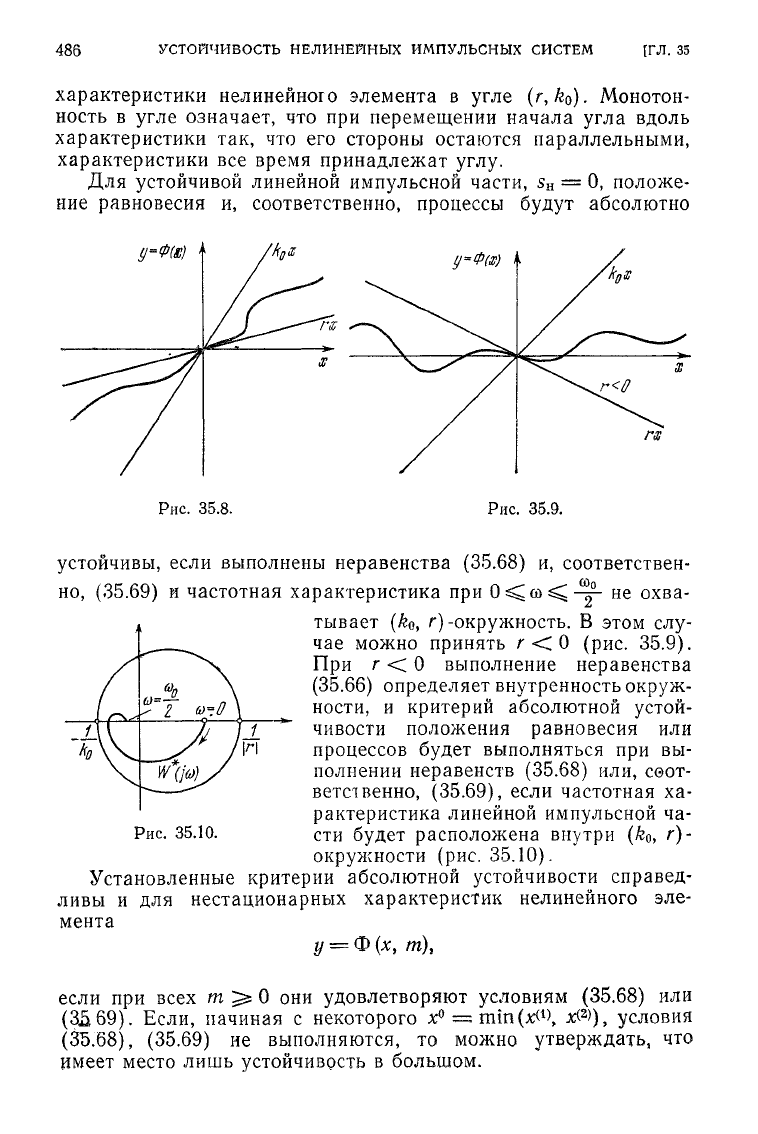
характеристики нелинейного элемента в

угле

(г,

Монотон-

ность в

угле

означает, что при перемещении начала

угла

вдоль

характеристики так, что его стороны остаются параллельными,

характеристики все время принадлежат

углу.

Для устойчивой линейной импульсной части,

= 0, положе-

ние

равновесия и, соответственно, процессы

будут

абсолютно

гх

Рис.

35.8.

Рис.

35.9.

устойчивы, если выполнены неравенства

(35.68)

и, соответствен-

но,

(35.69)

и частотная характеристика при

0<!со^-^-

не

охва-

тывает

(&о,

-окружность. В этом слу-

чае можно принять

0 (рис. 35.9).

При

г<0

выполнение неравенства

(35.66)

определяет внутренность окруж-

ности,

и критерий абсолютной устой-

чивости положения равновесия или

процессов

будет

выполняться при вы-

полнении

неравенств

(35.68)

или, соот-

ветственно, (35.69), если частотная ха-

рактеристика линейной импульсной ча-

Рис.

35.10.

сти

будет

расположена внутри

г)-

окружности (рис. 35.10).

Установленные критерии абсолютной устойчивости справед-

ливы и для нестационарных характеристик нелинейного эле-

мента

Ф(х,

т),

если при

всех

т ^ 0 они удовлетворяют условиям

(35.68)

или

(35.69). Если, начиная с некоторого

х°

—

min

(х^\

лЯ),

условия

(35.68),

(35.69)

не выполняются, то можно

утверждать,

что

имеет место лишь устойчивость в большом.

ЗАДАЧИ

48?

Задачи

35.1.

Показать, что при дополнительном ограничении на характеристику

нелинейного

элемента

с!ф(х)

частотное условие устойчивости принимает вид

[1 + а (1

е~^)\

(/со)

> 0.

Дать геометрическую интерпретацию этому частотному условию.

35.2. Показать, что для абсолютной устойчивости нелинейной импульсной

системы, частотная характеристика линейной импульсной части которой равна

0,572

0,028

необходимо и достаточно выполнение условия

<-*«-<

3,25.

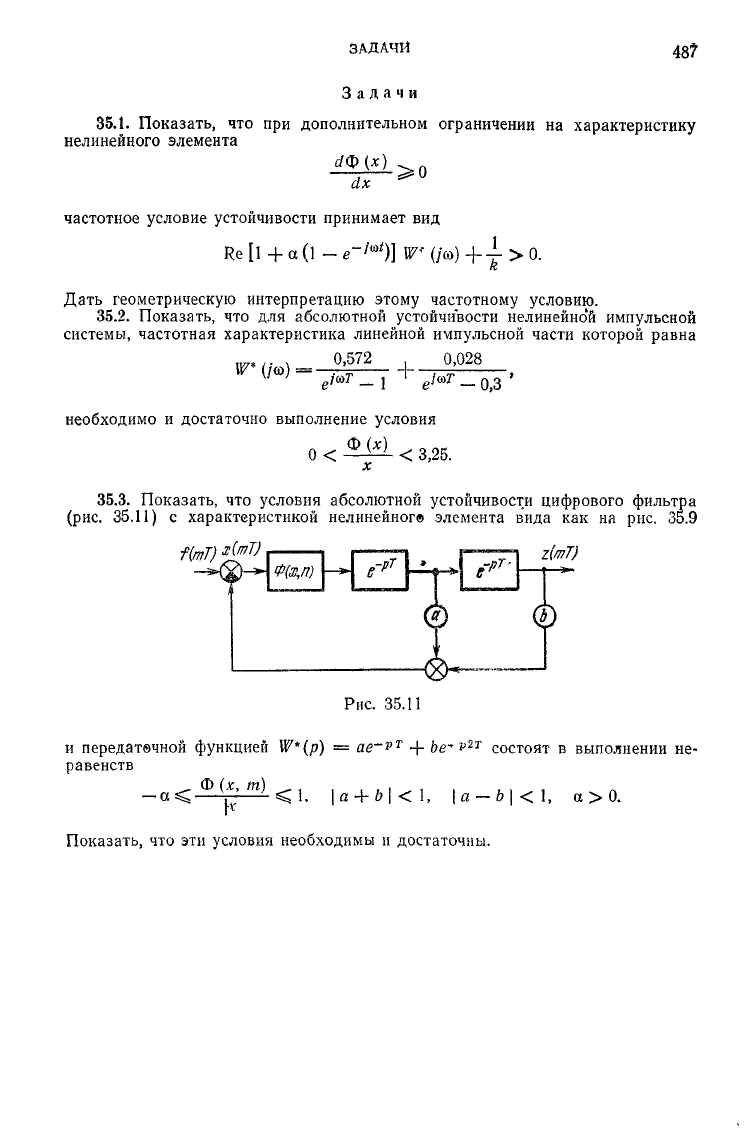
35.3. Показать, что условия абсолютной устойчивости цифрового фильтра

(рис.

35.11)

с характеристикой нелинейного элемента вида как на рис. 35.9

ПтТ)

z(mT)

Рис.

35.11

передаточной функцией

W*(p)

ae-v

be-

состоят в выполнении не-

равенств

(я,

т)

Показать,

что эти условия необходимы и достаточны.

Глава

ОЦЕНКИ

КАЧЕСТВА

СВОБОДНЫХ

ПРОЦЕССОВ

36.1. Мера быстродействия

нелинейных

импульсных систем

Будем говорить, что

быстродействие

или

степень

устойчиво-

сти нелинейной импульсной системы не меньше заданной |

если

lim

(mT)

= 0.

(36.1)

Для оценки быстродействия, или степени устойчивости, умножим

обе части уравнения свободного процесса

(35.4)

на

е^

тТ

Тогда

получим после очевидных преобразований

{mT)

f *

(mT)

—

((m

s) Т)

е^

("*-*>

(

m)e^

(36.2)

Вводя новые обозначения

(36.3)

запишем

уравнение

(36.2)

в такой форме:

(тГ)

-2]й((/п-5)Г)Ф

(mT),

m).

(36.4)

(шГ)

[пгТ)

Это уравнение соответствует некой преобразованной нелинейной

импульсной системе с нестационарной характеристикой нелиней-

36 1] МЕРА БЫСТРОДЕЙСТВИЯ НЕЛИНЕЙНЫХ СИСТЕМ 489

ного элемента

Ф(х

т) и видоизмененной линейной импульсной

частью, обладающей временной характеристикой w(mT). Оче-

видно,

если преобразованная система

будет

абсолютно устойчи-

вой,

т. е. если

lim

x*(mT)-=

lim

(mT)

(36.5)

т->оо

то быстродействие исходной нелинейной импульсной системы

будет

не меньше

Ъ-

Отсюда

следует,

что оценка быстродействия

исходной системы сводится к установлению абсолютной устой-

чивости преобразованной системы. Применим к последней об-

щий

критерий абсолютной устойчивости состояния равновесия,

который,

как мы отмечали уже выше, справедлив

для неста-

ционарных

характеристик. Найдем прежде всего частотную ха-

рактеристику линейной импульсной части преобразованной си-

стемы.

Так как согласно обозначению

(36.3)

(ml)

{mT)

(36.6)

то частотная характеристика, представляющая собой дискретное

преобразование Фурье,

будет

равна

{})

-О

или,

учетом

(36.6),

(mT)e-'«>

(36.7)

Назовем

W*(j(o

—

|o)

смещенной

частотной

характеристикой.

Тогда нелинейная импульсная система

будет

обладать быстро-

действием, не меньшим |

, если смещенная частотная характе-

ристика

будет

удовлетворять круговому критерию абсолютной

устойчивости. При этом, если выполнены ограничения, налагае-

мые на статический коэффициент линеаризации

k^(x)

(35.54),

то речь идет об оценке скорости достижения состояния равно-

весия.

Если же выполнены ограничения, налагаемые на диффе-

ренциальный

коэффициент линеаризации

k^(x)

(35.55), то

тогда

оценивается скорость установления процессов в нелиней-

ной

импульсной системе.

На

рис. 36.1 приведены смещенные частотные характери-

стики

W*(/(o

—

go),

которых система обладает степенью устойчи-

вости

|о, для случая устойчивой линейной импульсной части

490

ОЦЕНКИ

КАЧЕСТВА СВОБОДНЫХ ПРОЦЕССОВ

[ГЛ

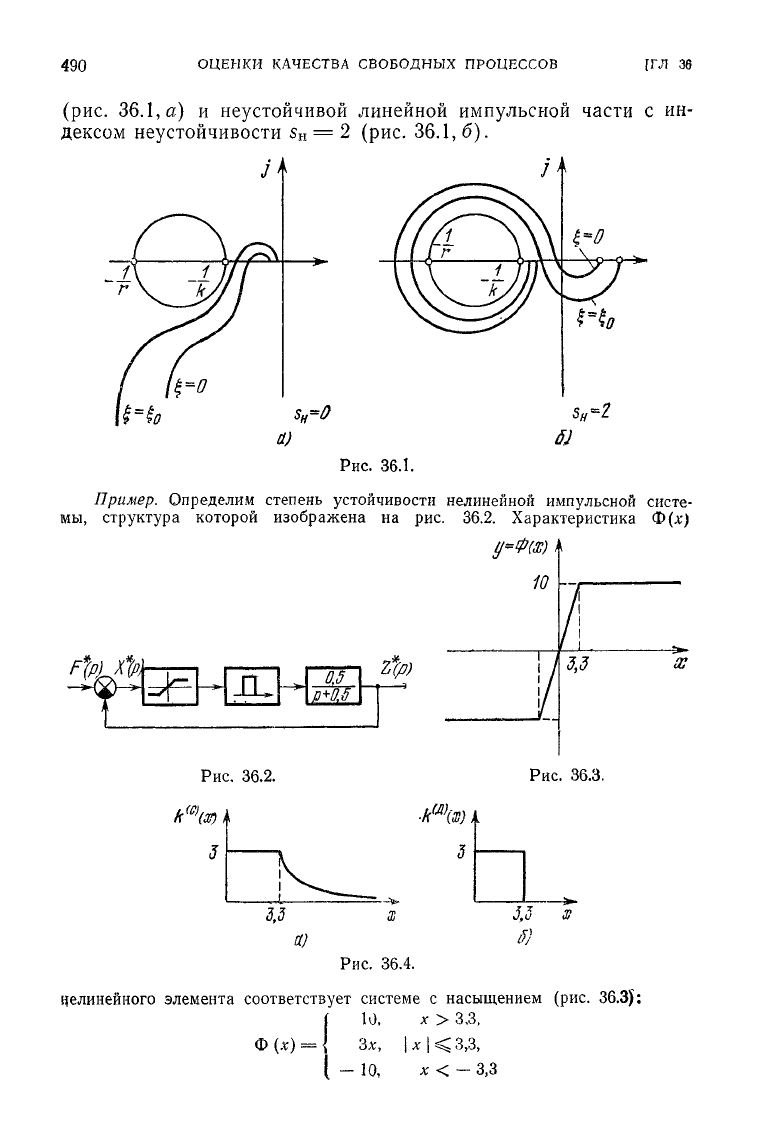
(рис.

36.1,

а)

и неустойчивой линейной импульсной части с ин-

дексом неустойчивости

(рис. 36.1, б).

/~\

Рис.

36.1.

Пример.

Определим степень устойчивости нелинейной импульсной систе-

мы,

структура которой изображена на рис. 36.2. Характеристика

Ф(л*)

Щр)

Рис.

36.2.

Рис.

36.3.

3,3

Рис.

36.4.

нелинейного

элемента соответствует системе с насыщением

(рис.

36.3):

(

10.

х>ЗД

(*)=!

з*,

з,з,

— 10, х <

-3,3

. 36?]

ОЦЕНКА

СУММАРНОГО

КВАДРАТИЧЕСКОГО

ОТКЛОНЕНИЯ

491

При

эгом

(рис 36.4, а, б) 0

>(*)

3 и 0

№(х)

3. Час-

тотная

характеристика линейной импульсной части определяется выраже-

нием

IF/-/'

(/со)

—г~-

Смещенная

частотная характеристика

будет

равна

п,*/,.

.ч

0,39

Она

для различных значений | = 0; 0,1;

0,2; 0,49 построена на рис. 36.5. Как

видно

из рис. 36.5, максимальная степень

устойчивости равна

0,49. Про-

ведя прямую —

-г-

= —

7Г5^-

— ~

°>

Рис.

36.5

для которой удовлетворяются крите-

рии

абсолютной устойчивости относительно смещенной частотной характери-

стики,

находим значение степени устойчивости нелинейной системы, не мень-

шее величины

= 0,49.

36.2. Оценка суммарного квадратического отклонения

Суммарное

квадратическое

отклонение,

вызываемое собствен-

ным

процессом, по аналогии с интегральным квадратическим от-

клонением

(см. § 19.3) определим как

ИЛИ

[х*(тТ)]\

т==0

/Ф=

(36.8)

(36.9)

если мы интересуемся суммарным квадратическим отклонением

от состояния равновесия, или, наконец,

/$=

&(xHmT),m),

т=0

(36.10)

если мы интересуемся суммарным квадратическим отклонением

от заданного процесса. Поскольку согласно

(35.5)

(х

(тТ),

/и)

= Ф

(х*

(пгТ)

(пгТ)) - Ф

(х

(пгТ))

(36.11)

и,

в частном

случае,

при

(mT)^0

становится равной

(х

(тГ),

/и)

= Ф

{шТ))

(36.12)

то мы рассмотрим наиболее общее выражение суммарного ква-

дратического отклонения

(36.10)

оценки

/$.

Точное значение