Цыпкин Я.З Основы теории автоматических систем

Подождите немного. Документ загружается.

462

УРАВНЕНИЯ

НЕЛИНЕЙНЫХ

ИМПУЛЬСНЫХ

СИСТЕМ

[ГЛ.

Продолжение

табл. 33.1

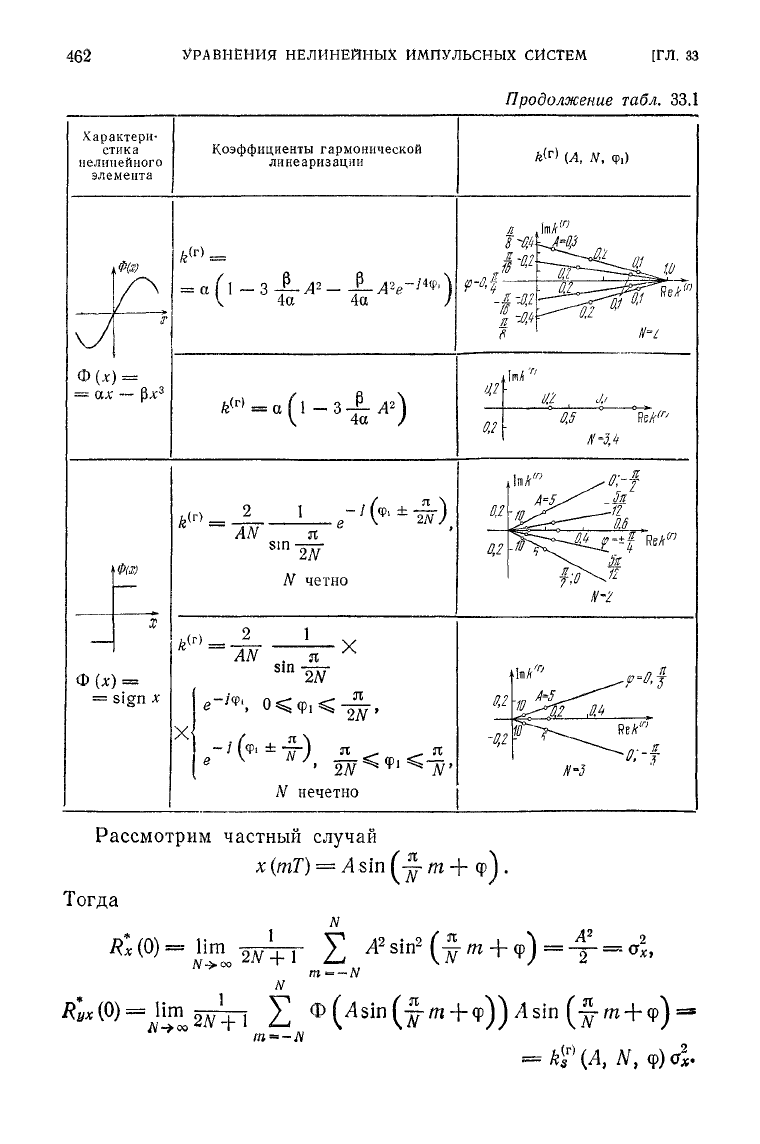
Характери-

стика

нелинейного

элемента

Коэффициенты

гармонической

линеаризации

(Л,

4а

{]

(г)

OJ^

">-—.

0,1

ах —

$х

0,2

Ы'

(г

{r)

•

четно

sin

sign

2iV

\ N

нечетно

Рассмотрим

частный случай

х(тТ)

sin

ф)

Тогда

^*(0)==

Пт

ОА

sin

(-тг

iv->oo

2N+\

П—N

33.3]

УРАВНЕНИЯ

НЕЛИНЕЙНЫХ

ИМПУЛЬСНЫХ

СИСТЕМ

463

значит, согласно

(33.19),

(33.20)

iCT)

(<&)=kU(A

q>).

В табл. 33.1 приведены характеристики нелинейных элемен-

тов и соответствующие им коэффициенты гармонической линеа-

ризации.

33.3. Уравнения нелинейных импульсных систем

Уравнения нелинейных импульсных систем, блок-схема кото-

рых приведена к виду рис.

33.1,

образуются из уравнения линей-

ной

импульсной части

z(mT)

{(m

s)T)x

{sT),

(33.21)

уравнения нелинейного элемента

(тТ)

Ф(х(тТ))

(33.22)

условия замыкания

(шТ)

= f

(шТ)

(шТ).

(33.23)

Исключая из уравнений

(33.21)

—

(33.23)

промежуточные пере-

менные

Xi(mT)

z(mT)

получаем уравнение относительно

ошибки:

(пгГ)

= f (mT)

{{m

s) Т) Ф (х

(sT)).

(33.24)

Если же исключить

Xi(mT)

x(mT)

то получим уравнение от-

носительно выходной величины:

(mT)

=Zw({m-s)T)&

(sT)

(sT)).

(33.25)

Уравнения

(33.24)

(33.25)

представляют собой нелинейные

суммарные уравнения относительно величин, характеризующих

состояние системы в дискретные моменты времени t = mT. Под-

вергая уравнения

(33.24)

(33.25)

D-преобразованию

и учиты-

вая,

что

D{f(mT)}

F*(p),

получим уравнения относительно изображений:

(р)

F* (р)

(р) D {Ф (х

(mT))}

(33.26)

(р)

W* (р) D {Ф (/ (mT)

(тГ))}.

(33.27)

Здесь

464 УРАВНЕНИЯ НЕЛИНЕЙНЫХ ИМПУЛЬСНЫХ СИСТЕМ

{ГЛ

— передаточная функция линейной части импульсной системы.

Уравнения

(33.26)

(33.27)

содержат

изображение нелинейной

функции

от искомого решения

0{Ф(х(тТ))}.

сожалению, это

изображение не выражается в явной форме через Х*(р) =

—

D{x(mT)}.

Поэтому уравнения (33.26),

(33.27)

носят услов-

ный

характер. В отличие от уравнений нелинейных непрерывных

систем

— нелинейных интегральных уравнений, уравнения нели-

нейных

импульсных систем — нелинейные суммарные уравнения

(33.24),

(33.25)

представляют собой рекуррентные соотношения

позволяют определить значения ошибки процесса

х(пгТ)

в по-

следовательные моменты времени

пгТ

(пг

= О, 1, 2, 3, ...). По-

этому задача построения процесса в нелинейной импульсной си-

стеме при заданном внешнем воздействии решается довольно

просто.

Что же касается исследования свойств этого процесса,

то здесь имеются те же возможности, что и для непрерывных

систем.

Задачи

33.1.

Вывести выражения коэффициентов гармонической линеаризации

для типовых нелинейных элементов, приведенных в табл. 33 1.

33.2. Установить отличие коэффициентов статической, дифференциальной,

гармонической и стохастической линеаризации нелинейных элементов в непре-

рывных и дискретных системах.

Глава

ПРОЦЕССЫ

НЕЛИНЕЙНЫХ

ИМПУЛЬСНЫХ

СИСТЕМАХ

34.1. Построение процессов

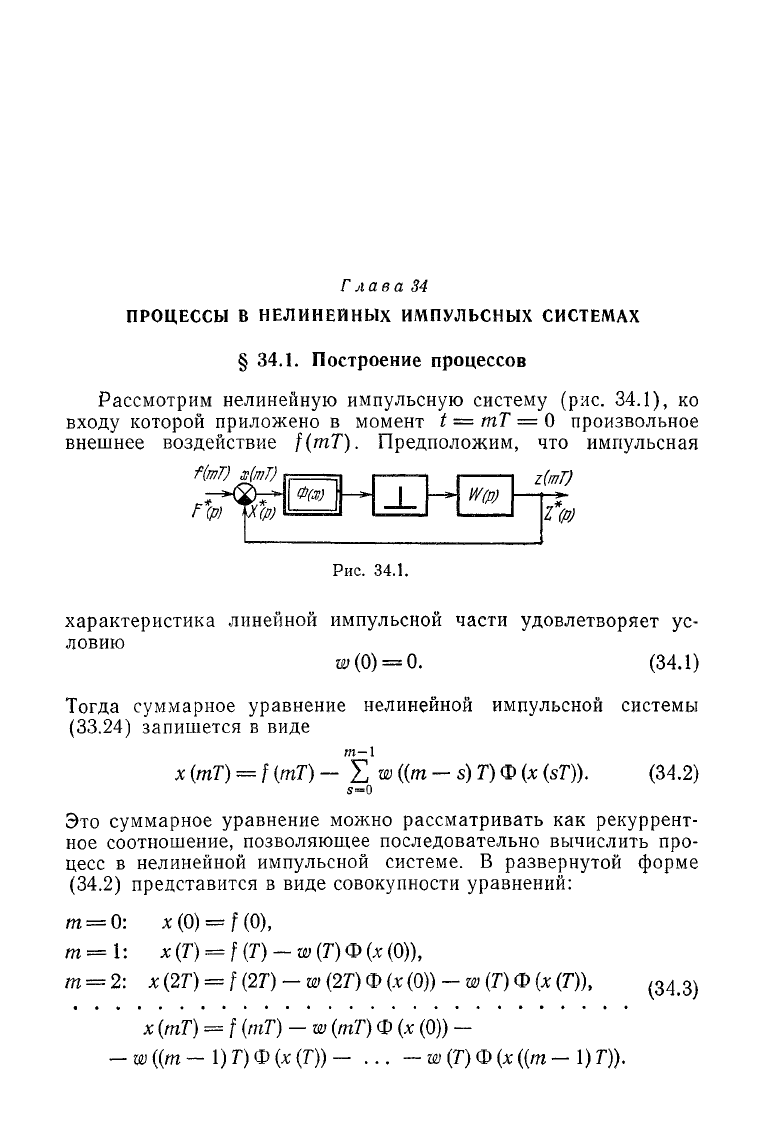
Рассмотрим нелинейную импульсную систему (рис. 34.1), ко

входу

которой приложено в момент t = тТ = 0 произвольное

внешнее воздействие

f(mT).

Предположим, что импульсная

ПтпТ)

F(p)

\Хф)

Ф(ЗВ)

W(p)

z(mT)

Рис. 34.1.

характеристика линейной импульсной части удовлетворяет ус-

ловию

ш(0)

(34.1)

Тогда суммарное уравнение нелинейной импульсной системы

(33.24)

запишется в виде

(тТ)

((пг

s) Т) Ф (х

(sT)).

(34.2)

Это суммарное уравнение можно рассматривать как рекуррент-

ное

соотношение, позволяющее последовательно вычислить про-

цесс в нелинейной импульсной системе. В развернутой форме

(34.2)

представится в виде совокупности уравнений:

(34.3)

*(Г)

/(Г)-а>(Г)Ф(*(0)),

2: х

(2Г)

Ф (х (0))

(T)

Ф (х

(Г)),

х {пгТ)

(mT)

(тТ)

Ф (х (0))

...

-о;(Г)Ф(*((т--1)Г)).

466

ПРОЦЕССЫ

НЕЛИНЕЙНЫХ ИМПУЛЬСНЫХ СИСТЕМАХ

[ГЛ. 34

Из

этих уравнений наглядно видна возможность

последователь-

ного вычисления процесса

x(mT)

—

О,

1, 2, ..., по

заданным

f(mT),

w(mT) и

Ф(х(тТ)). Некоторое неудобство рекуррент-

ного соотношения (34.2) состоит

в том, что с

ростом

m в нем

число слагаемых неограниченно возрастает.

Для

того чтобы

осво-

бодиться

от

этого, воспользуемся уравнением нелинейной

им-

пульсной системы относительно изображений (33.26):

(р)

D {Ф

(х

(mT))h

(34.4)

где

W*(p)

D{w(mT)},

или,

развернутой форме

при

выполнении условия (34.1),

При

этом порядок

(р) отличен

от 0.

Умножая числитель

знаменатель (34.5)

на

е~Р

пТ

запишем

(р)

виде

Ъ.ш

РТ±Ь„*

[±_^j^e^^

(34e6)

-г

{

Подставляя W* (р) (34.6)

(34.4)

освобождаясь

полученном

уравнении

от

знаменателя,

запишем (34.4)

таком виде:

(

-J-

е~~

рт

... +

е~~

рпТ

X* (р)

—

(Ь[е-

рТ

Ь'

е~

р2Т

+ ...

+Ь

е^

рпТ

)О{Ф{х{тТ))}.

(34.7)

Переходя

(34.7)

от

изображений

оригиналам

на

основании

теорем линейности

запаздывания, получим

х(пгТ)

-\-

х((/и

—

1) Т)

... +

х{(пг

—

п)Т)

(шТ)

a\f

((m—l)T)+

... +

a'J

((m

— n)T)

—

Ь[Ф

(x((m

1)Г))

Ь'

Ф(х(пг

-2)Т))~

...

-Ь'

Ф(х((т-п)Т)),

(34.8)

где

х((т

—

п)Т),

({m

—

п)Т)

при

<п

следует

полагать

рав-

ными

нулю. Таким образом, получим

из

(34.8)

для

пг

(пгТ)

(34.9)

34.2] ВЫНУЖДЕННЫЕ И СВОБОДНЫЕ ПРОЦЕССЫ 467

и для

т^п

(тТ) =

v-i

)

(34.90

Эти рекуррентные соотношения содержат конечное число слагае-

мых, не превышающее

Зя+1,

где

—

порядок передаточной

функции

линейной части импульсной системы. Таким образом,

отличие

от

нелинейных

непрерывных

систем,

в нелиней-

ных

импульсных

системах

при

заданном

внешнем

воздей-

ствии

принципиально

всегда

может

быть

построен

про-

цесс,

вызванный

этим

воздействием.

Этот факт

будет

иметь важное значение при цифровом моде-

лировании

непрерывных систем.

34.2. Вынужденные и свободные процессы

Назовем

вынужденным

процессом

процесс

(тТ),

вызывае-

мый

внешним ограниченным воздействием, приложенным в мо-

мент времени, отстоящий от момента наблюдения на бесконечно

большой интервал времени. Предположим, что внешнее воздей-

ствие приложено к системе в момент времени k —

тогда по-

ведение этой системы

будет

описываться суммарным уравнением

вида

—

s)T)d>(x(sT)).

(34.10)

Устремляя в (34.10)

—оо,

получаем уравнение вынужден-

ного процесса:

(mT)

f{mT)-

w((m-~k)T)<D(x

(kT)),

или,

после замены

— k на s и,

значит,

k на m — s,

оо

(mT)

{шТ)

(sT) Ф

{х

((/и

Г)).

(34.11)

Свободный

процесс

(тТ)

определяется разностью между об-

щим

процессом х(пгТ) и вынужденным процессом

(тТ),

т.е.

{mT)

x{mT)-x

(mT).

Полагая

в уравнении (34.2)

468 ПРОЦЕССЫ В НЕЛИНЕЙНЫХ ИМПУЛЬСНЫХ СИСТЕМАХ [ГЛ.

где /.

(тТ)—исчезающее

внешнее воздействие, характеризую-

щее ненулевое состояние импульсной системы в момент прило-

жения

внешнего воздействия, вычитая из него уравнение выну-

жденного процесса (34.11), получаем уравнение свободного

процесса:

((m

- s) T) [Ф

{sT)

(sT)) - Ф

(sT))].

(34.12)

В этом уравнении

оо

U(mT)=

w((m-s)T)O(x

(mT))

w(sT)Q)(x

'((m-s)T))

—oo

S«0

— воздействие, которое, наряду с

№(пгТ),

вызывает свобод-

ный

процесс.

Свободный

процесс

вызывается

как

самим

фактом

прило-

жения

внешнего

воздействия,

так и

ненулевым

начальным

состоянием.

34.3. Возможные процессы

Если

положить в уравнении вынужденного процесса

(34.11)

f(mT)~0,

(34.13)

то мы получим уравнения, определяющие возможные стационар-

ные

состояния нелинейной импульсной системы при отсутствии

внешнего воздействия. Обозначив эти стационарные состояния

ст

(тТ)

получаем из

(34.12)

при условии

(34.13)

уравнение

стационарных состояний:

оо

дет

(тГ

)

= -

(sT) Ф

ст

((от - s) T)).

(34.14)

Стационарные

состояния

могут

соответствовать положениям

равновесия системы либо периодическим процессам, по в отли-

чие от нелинейных непрерывных систем, где период этих процес-

сов может быть, вообще говоря, любым, в нелинейных импульс-

ных системах периодические процессы имеют период, всегда

кратный

периоду повторения импульсного

элемента.

Эти процес-

сы,

строго говоря, нельзя назвать автономными, так как им-

пульсная система

даже

при отсутствии внешних воздействий не

является автономной из-за наличия импульсного элемента. По-

этому такие процессы, строго говоря, не являются автоколеба-

34.4]

ВЛИЯНИЕ

КВАНТОВАНИЯ

ПО

УРОЁМЮ

409

ниями.

Это обстоятельство объясняет сложность процессов, ко-

торые

могут

возникать в нелинейной импульсной системе. По-

этому

мы ограничимся исследованием только периодиче-

ских процессов.

34.4.

Влияние

квантования

по

уровню

Общие свойства процессов в непрерывных системах,

рассмо-

тренные в § 16.4, остаются справедливыми и для импульсных си-

стем. Поэтому здесь мы не

будем

повторяться и подробнее рас-

смотрим влияние квантования по уровню — нелинейности, спе-

цифической

для цифровых автоматических систем. Квантование

ц~Ф(Х)

Х-

17^

«2?

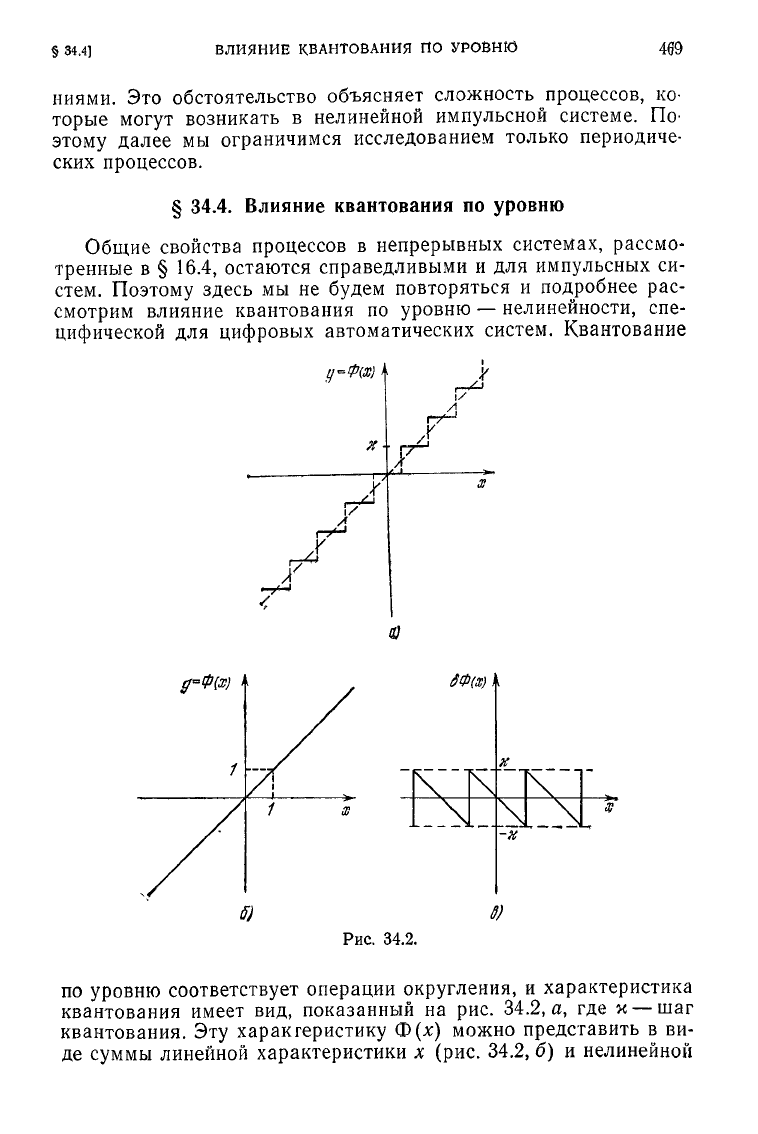
Рис.

34.2.

по

уровню

соответствует

операции округления, и характеристика

квантования

имеет вид, показанный на рис. 34.2, а, где

—

шаг

квантования.

Эту характеристику

Ф(х)

можно представить в ви-

де суммы линейной характеристики х (рис. 34.2, б) и нелинейной

470

ПРОЦЕССЫ

НЕЛИНЕЙНЫХ ИМПУЛЬСНЫХ СИСТЕМАХ

[ГЛ.

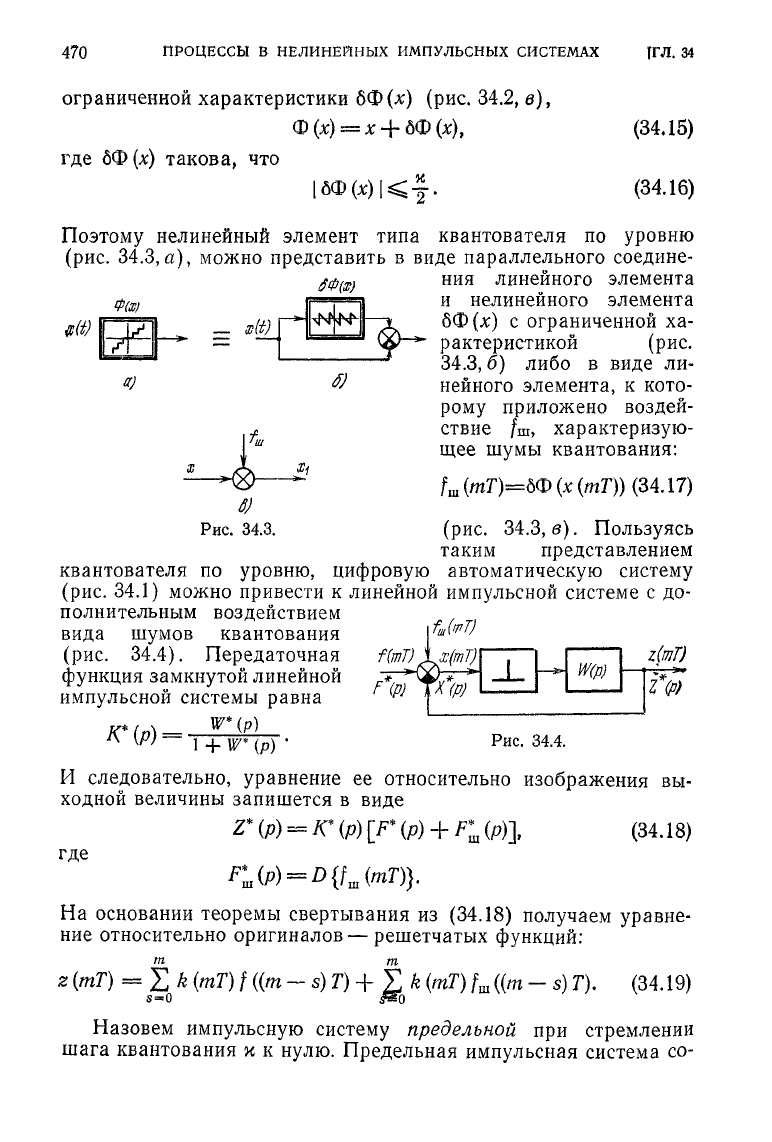
ограниченной

характеристики

8Ф(х)

(рис.

34.2,

в),

ф(х)^х

6Ф(х)

где

6Ф(я)

такова,

что

|бФ(х)|<|.

(34.15)

(34.16)

Поэтому нелинейный элемент типа квантователя

по

уровню

(рис.

34.3,

а),

можно представить

виде параллельного соедине-

ния

линейного элемента

(х}

»|

нелинейного элемента

6Ф(я)

ограниченной

ха-

рактеристикой

(рис.

34.3,

б)

либо

виде

ли-

нейного

элемента,

кото-

рому приложено воздей-

ствие /

, характеризую-

щее шумы квантования:

(mT)=№(x(mT))

(34.17)

Рис

34.3.

(рис.

34.3,

в).

Пользуясь

таким

представлением

квантователя

по

уровню, цифровую автоматическую систему

(рис.

34.1)

можно привести

линейной импульсной системе

с до-

полнительным воздействием

вида шумов квантования

(рис.

34.4). Передаточная

функция

замкнутой линейной

импульсной системы равна

ПтТ)

1фТ)

W(p)

z(mT)

Z(p)

Рис.

34.4.

следовательно, уравнение

ее

относительно изображения

вы-

ходной величины запишется

виде

(р)

—

К* (р)

[F*

(р)

(/?)],

(34.18)

где

На

основании теоремы свертывания

из

(34.18)

получаем уравне-

ние

относительно

оригиналов—решетчатых

функций:

(mT)

f((m-

)T)+Yk

(mT)

((m

-s)T).

(34.19)

Назовем

импульсную систему

предельной при

стремлении

шага квантования

нулю. Предельная импульсная система

со-

34.4]

ВЛИЯНИЕ

КВАНТОВАНИЯ ПО

УРОВНЮ

471

ответствует линейной системе при отсутствии воздействия шума

квантования;

ее уравнение:

(тТ)

(sT) f

((m

- s)

Г).

(34.20)

Обозначая через

(niT)

{mT)

—

(mT)

эффект,

вызываемый квантованием

по

уровню, находим, вычитая

из

уравнения (34.19) уравнение (34.20),

()Е

Оценим

6z(mT). Очевидно,

(шТ)

(sT)

((т

- s) T) |. (34.21)

Но в

силу

(34.16) и (34.17)

Поэтому неравенство (34.21) можно усилить как за счет замены

|/in((frc

—

)^)1

правой части, так и за счет увеличения верх-

него предела суммирования m до оо. Таким образом, получим

Для устойчивых линейных импульсных систем, как следует из

определения устойчивости,

оо

Z\k(sT)\

= C

<oo,

(34.22)

где С —

податливость

системы, и, значит, верхняя граница

\8z(mT)\

всегда

будет

меньше некоторой фиксированной вели-

чины,

а именно:

я/

пг

Таким

образом,

наибольшее

отклонение

процесса,

вызываемое

квантова-

нием

по

уровню,

не

превосходит

произведения

податливо-

сти

системы

на

половину

шага

квантования-