Цыпкин Я.З Основы теории автоматических систем

Подождите немного. Документ загружается.

362

ОСНОВНЫЕ

СТРУКТУРЫ

ИМПУЛЬСНЫХ

СИСТЕМ

[ГЛ. 24

воздействиями F*(p) и

№*

лф

(р)

(р),

приложенными в разных

точках системы (рис.

24.3,6).

Уравнение этой системы, состав-

ляемое по обычным правилам, представится з виде

W*(p)

(р)

г;

(р)

(р)}

W—

+ w

{p)

КР)+

+ г

* (р)

Или,

так как согласно теореме 5 приложения 3

(Р)

г;

(р)

г;

(р)

то окончательно получим

Уравнение же относительно ошибки X* (р)

(р) — Z* (р) пред-

ставится в виде

Г(

При

выборе

(р)

(24.10)

получаем тождественное равенство нулю ошибки:

Таким

образом,

при

передаточной

функции

дискретного

фильтра

W*.(p),

равной

обратной

передаточной

функции

непрерывной

ча-

сти,

система

воспроизводит

входное

воздействие

без

иска-

жений,

т. е.

Z*(p)^F*(p).

(24.11)

Как

и в непрерывных системах, условие (24.10) не может

быть точно выполнено, и поэтому не могут быть выполнены и

условия идеального воспроизведения

(24.11).

ПшТ)

W*(

)

ftp)

Рис

24.4

разомкнуто-замкнутой системе близка по структуре система

условной

обратной

связью

(рис. 24.4). Эту систему можно так-

же рассматривать как систему с двумя внешними воздействиями,

ЗАДАЧИ

363

изображения которых равны

Wl^{p)F{p)

и соответственно

.(р)

F (р), приложенными в различных точках. Уравнение

такой системы запишется в виде

(Р)

При

1 +

Г*

(р)

система с условной обратной связью

соответствует

ранее рас-

смотренной разомкнуто-замкнутой системе.

Задачи

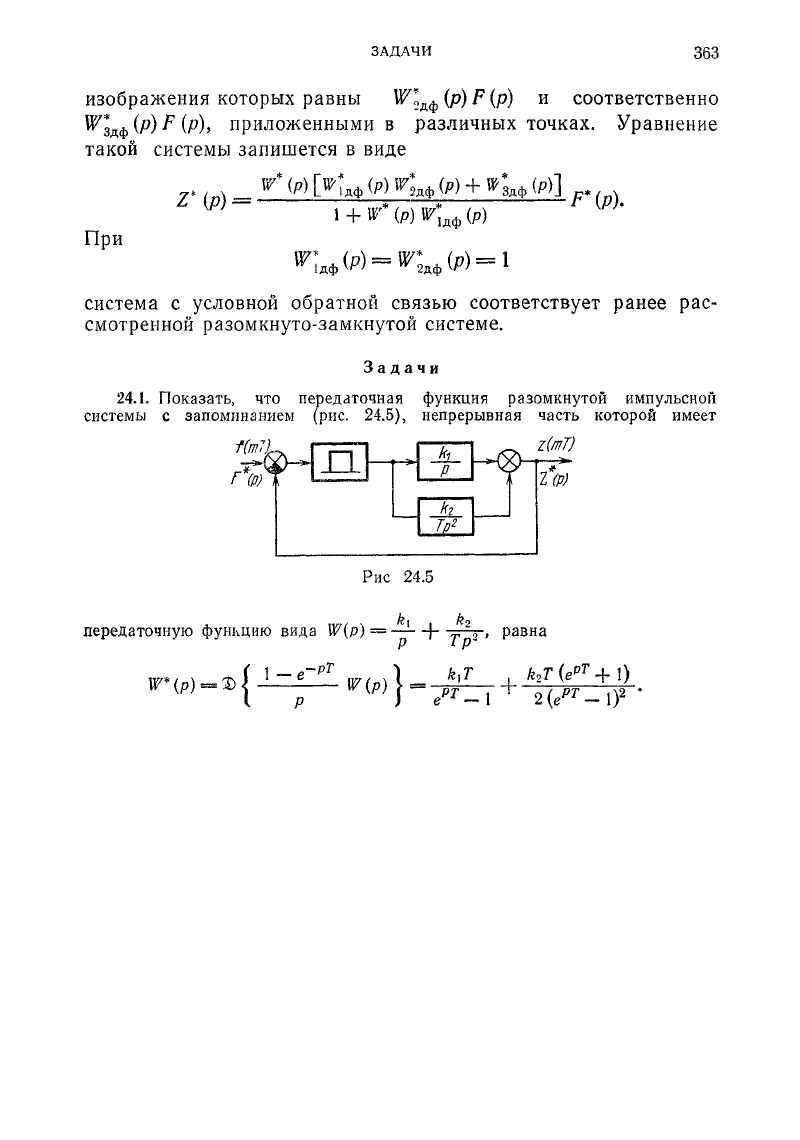
24.1.

Показать, что передаточная функция разомкнутой импульсной

системы с запоминанием (рис. 24.5), непрерывная часть которой имеет

JELh

кг

передаточную функцию вида W{p)

Рис

24.5

Гр»'

W(P)

—'

И7(р)

равна

T(e"

+\)

Глава

ОСНОВНЫЕ

ХАРАКТЕРИСТИКИ

ИМПУЛЬСНЫХ

СИСТЕМ

25.1.

Законы

управления

Простейшие

законы управления, такие, как пропорциональ-

ный

(П), интегральный (И), пропорционально-интегральный

(ПИ),

могут

формироваться в непрерывной части системы по-

добно

тому,

как это делалось в непрерывных автоматических си-

стемах (см. § 8.1). Изменение характеристик непрерывной части

системы в конечном итоге влияет на свойства замкнутой систе-

мы в целом. По аналогии с подобными непрерывными законами

управления можно формировать дискретные законы регулиро-

вания

в дискретном фильтре или ЦВУ путем выбора передаточ-

ной

функции

W^(p)

nBy

(p)

(p).

Так, при

(р)

y^T

*,(!-

РГ

(

25Л

)

мы получаем пропорциональный суммарно-разностный (ПСР)

закон

управления. Составляющие, входящие в (25.1),

РТ РТ

1 е

g-рт

=.—

—

(25 2)

соответствуют

суммированию и взятию первой разности входной

решетчатой величины.

В отличие от операции

дифференцирования,

которая не мо-

жет быть точно осуществлена, взятие разности не представляет

особого

труда.

Подставляя

(25.2)

в (25.1), получим после при-

ведения к общему знаменателю

(Ъ

-L.

J-

с£рТ

(и

рТ

117*

(п\

гс—\

~г

к\)

\KQ

-f-

к\)

-f

к\

Отсюда видно, что стандартные законы управления соответ-

ствуют

выборам конкретных видов коэффициентов передаточных

функций

дискретного фильтра или ЦВУ (24.3). В общем же слу-

чае дискретные фильтры и ЦВУ позволяют реализовать разно-

25.2]

ДИСКРЕТНЫЕ

ПЕРЕДАТОЧНЫЕ

ФУНКЦИИ

365

образные сложные законы управления, что открывает широкие

возможности получения высококачественных импульсных систем

управления. Поэтому целесообразно далее рассмотреть струк-

туру

импульсной автоматической системы, которая содержит

дискретный фильтр или ЦВУ в контуре управления.

25.2. Дискретные передаточные функции

разомкнутых импульсных систем

В отличие от непрерывных систем, для которых передаточ-

ные

функции составляются непосредственно по уравнениям эле-

ментов,

в импульсных системах передаточные функции опреде-

ляются по временной характеристике или передаточной функции

непрерывной

части. Соответствие

между

ними устанавливается

D-

или

©-преобразованиями.

Так, если передаточная функция

приведенной

непрерывной части равна

W(p)

S(p)WAp),

то

передаточная функция разомкнутой импульсной системы

W*(p),

которую мы

будем

называть для краткости дискретной

передаточной функцией, находится в

результате

©-преобразова-

ния

от

W(p),

т. е.

(р)

{W (р)}

(p)}.

Для прямоугольной формы импульса

значит, согласно определению

©-преобразования

(23.5)

&=_оо

Мы

здесь предполагаем, что начальное значение импульсной ха-

рактеристики непрерывной части равно нулю, т.е.

(0)=0.

В противном

случае

к правой части

(25.3)

следует

добавить сла-

гаемое

(0)/2.

Тогда получим, что

Г{Р)

_^л+£

•-.

Wm{р

_ ,

(25

Соотношения

(25.3),

(25.4)

определяют дискретную передаточ-

ную функцию разомкнутой импульсной системы через передаточ-

ную функцию непрерывной части в виде бесконечного ряда.

Можно

найти выражение дискретной передаточной функции

разомкнутой импульсной системы в конечной форме.

366 ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИМПУЛЬСНЫХ

СИСТЕМ

[ГЛ. 2$

Предположим, что в общем

случае

^—wu-

(25

где

Р(р),

Q(p)

— многочлены степени

и п соответственно.

Обозначая через

рь

р2,

...,

полюсы передаточной функции

предполагая их отличными

друг

от

друга,

представим

(25.5)

виде разложения:

£Шт^-

(25

v=»l

Подставляя

(25.6)

в выражение для

(р), получим

Меняя

последовательность суммирования и взятия

S-преобразо-

вания

и вынося за знак

©-преобразования

функции

е^

на осно-

вании

теорем ©-преобразования (см. приложение 2), получим

(25.7)

V—1

Но

поскольку

Р(Р-

Pv) Р- Pv

ТО

Пользуясь таблицей соответствий (таблица П.2 приложения 2),

получаем

Подставляя

(25.8)

в (25.7), после очевидных преобразований

получим

Если

один из полюсов

(p),

например

равен нулю,

= О,

то

п-е

слагаемое в

(25.6)

становится неопределенным. Раскры-

вая

неопределенность, получим

(Рп)

pT_J>n

Q'(0)

^-Г

25.2]

ДИСКРЕТНЫЕ

ПЕРЕДАТОЧНЫЕ

ФУНКЦИИ

367

Неопределенность возникает также при наличии кратных

полю-

сов.

Она может быть раскрыта обычным способом.

Передаточную функцию разомкнутой импульсной системы

(25.9)

можно представить в виде дробно-рациональной функции.

Из

(25.4)

или

(25.9)

следует,

что

W*{p

jk<bo)

W(p),

±1,

±2,

...

(25.10)

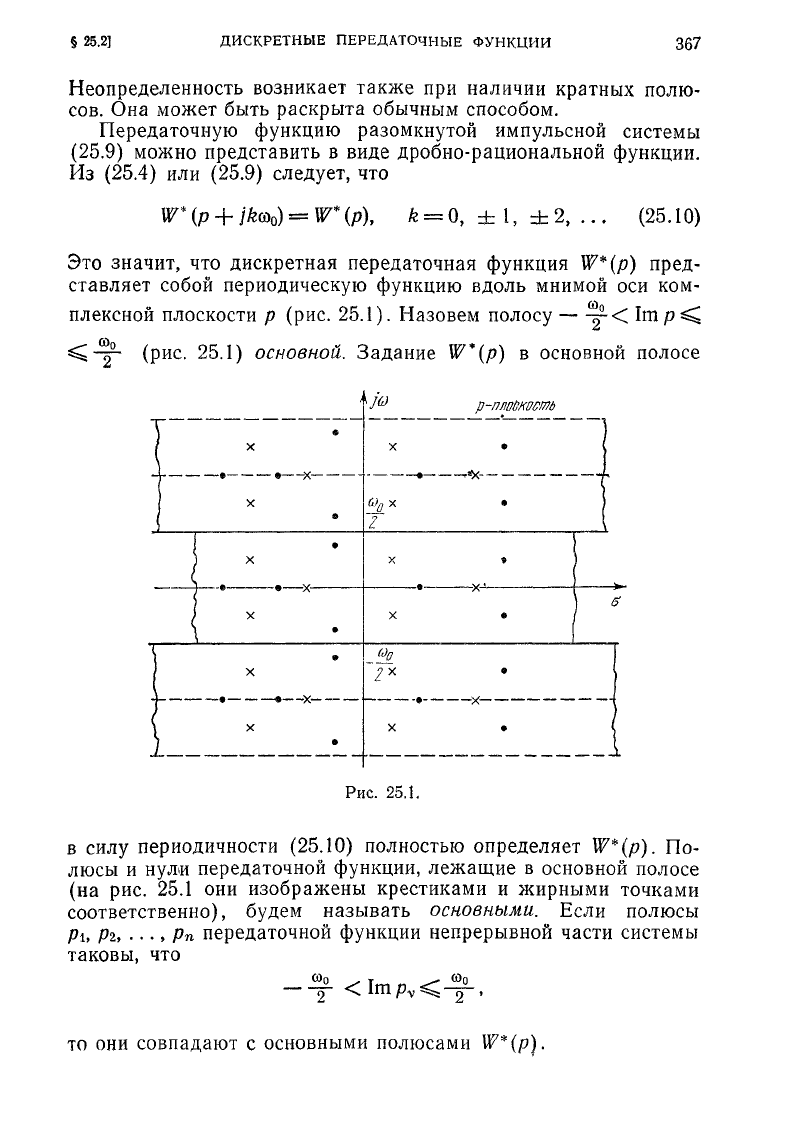
Это значит, что дискретная передаточная функция W*(p) пред-

ставляет собой периодическую функцию вдоль мнимой оси ком-

плексной

плоскости р (рис. 25.1). Назовем полосу —

-™-<

Imp^

^-у-

(рис.

25.1)

основной.

Задание

W*(p)

в основной полосе

р-плойжть

Рис.

25.1.

силу периодичности

(25.10)

полностью определяет

W*(p).

По-

люсы и нули передаточной функции, лежащие в основной полосе

(на

рис. 25.1 они изображены крестиками и жирными точками

соответственно),

будем

называть

основными.

Если полюсы

ри

р2,

. • •,

Рп

передаточной функции непрерывной части системы

таковы, что

<Ч

1ГП

"~п~"

то они совпадают с основными полюсами

W*{p).

368 ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИМПУЛЬСНЫХ СИСТЕМ

ГГЛ.

В общем

случае

дискретную передаточную функцию разо-

мкнутой системы можно представить в виде дроби

где

Q*(p)

Р*(р)—многочлены

е^

степени п

и,

вообще го-

воря,

п — 1 соответственно. Таким образом, импульсная переда-

точная функция имеет п полюсов и п — 1 нулей.

Дискретную передаточную функцию часто удобно предста-

вить в форме

(п) -

{р)

(р)

где

(p)

и Р*

(р)

— нормированные многочлены степени

—

п — 1 соответственно, т. е. такие, что

Р*

(0)

— коэффициент усиления разомкнутой импульсной

систехмы.

Введем следующие числовые показатели дискретной переда-

точной функции.

Порядок

п определяется степенью знаменателя дискретной

передаточной функции

IF*(p).

Степень

определяется разностью степеней знаменателя

числителя дискретной передаточной функции W*(p). Как пра-

вило,

степень

W*(p)

равна

= /г —

(/г

—

Индекс

неустойчивости

определяется числом правых по-

люсов

W*(p).

Индекс

астатизма

определяется числом полюсов

W*(p),

равных нулю.

Индекс

неминимально-фазовости

%ф

определяется числом

правых нулей

W*(p).

Через эти числовые показатели далее

будут

выражены раз-

личные свойства импульсных систем.

25.3. Дискретные передаточные функции

типовых импульсных систем

Найдем передаточные функции ряда конкретных типовых им-

пульсных систем.

Рассмотрим импульсную систему первого порядка

(рис.

25.2, а), состоящую из импульсного элемента с прямоуголь-

ной

формой импульса и линейной

части,

передаточная функция

25.3] ДИСКРЕТНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ТИПОВЫХ СИСТЕМ 369

которой равна

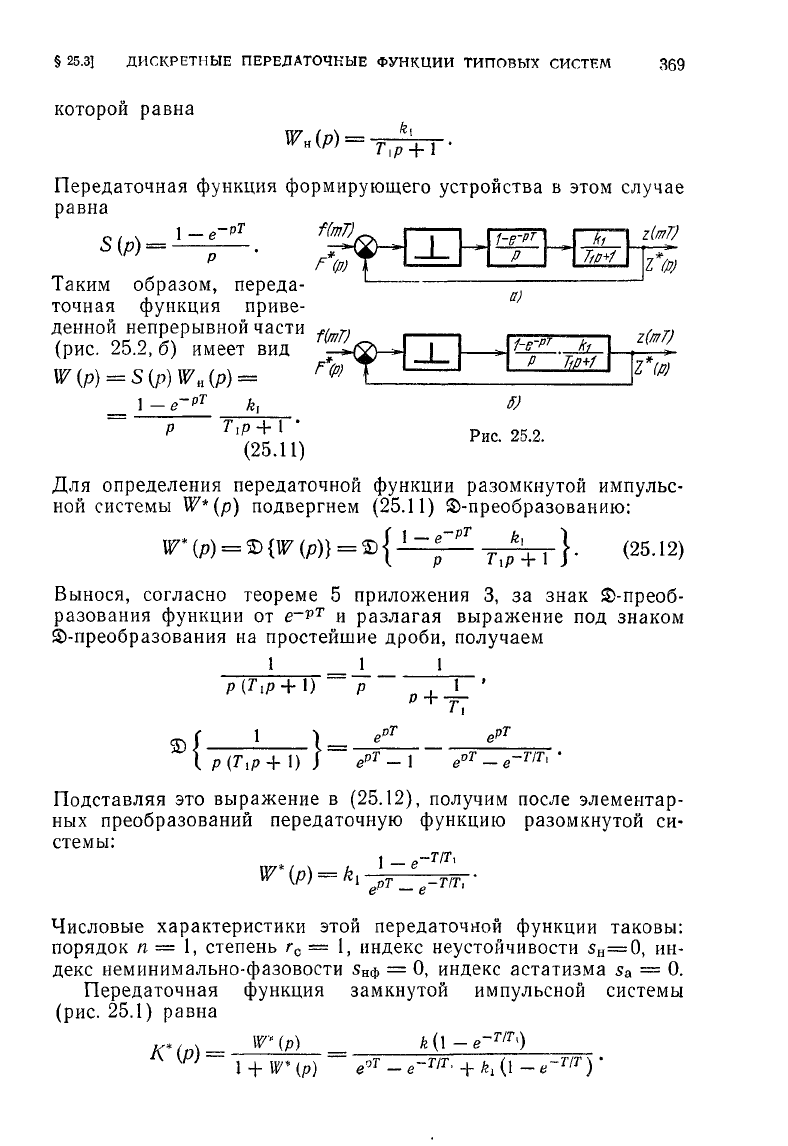
Передаточная функция формирующего устройства в этом

случае

равна

с,

(р)

е-»

Таким образом, переда-

точная функция приве-

денной непрерывной части

(рис.

25.2,

б) имеет вид

W(p)

S{p)W

(p)

z(mT)

1Ф)

а)

M-L-

Ttf+/

z(mT)

Z*(P)

(25.ll)

Рис.

25.2.

Для определения передаточной функции разомкнутой импульс-

ной

системы

W*(p)

подвергнем

(25.II)

{p) =

Тгр-

(25.12)

Вынося, согласно теореме 5 приложения 3, за знак

©-преоб-

разования функции от

e~v

и разлагая выражение под знаком

P(TiP

р-

[)

•}-

рТ

Подставляя это выражение в (25.12), получим после элементар-

ных преобразований передаточную функцию разомкнутой си-

стемы:

Числовые характеристики этой передаточной функции таковы:

порядок п = 1, степень

= 1, индекс неустойчивости

=0,

ин-

декс неминимально-фазовости

= 0, индекс астатизма

Передаточная функция замкнутой импульсной системы

(рис.

25.1) равна

(р)

k{\ —

T/Tl

)

\Г

(р)

оТ

e-W'

e-W)

К*(Р)-

370

ОСНОВНЫЕ

ХАРАКТЕРИСТИКИ

ИМПУЛЬСНЫХ

СИСТЕМ

[ГЛ. 25

Рассмотрим импульсную систему второго порядка (рис. 25.3),

состоящую из простейшего импульсного элемента и линейной

части, передаточная функция которой равна

Формирующее устройство в этом

случае

отсутствует,

т. е.

Поэтому передаточные функции приведенной и неприведенной

непрерывной

части совпадают, т. е.

и,

значит,

или,

после преобразования,

{\ -

Числовые характеристики этой передаточной функции таковы:

порядок

п = 2, степень

= 1, индекс неустойчивости

= 0,

Г(р)

p(T

p4)

z(m/J

Z*(p)

Рис 25.3.

индекс

неминимально-фазовости

0, индекс астатизма

Передаточная функция замкнутой системы

будет

равна

(р)

TIT

т/т

))

25,4.

Уравнения импульсных систем

Зная

передаточные функции замкнутых систем, можно урав-

нения

этих замкнутых систем относительно изображений запи-

сать в виде

Гр).

(25.13)

По

определению дискретного преобразования Лапласа

§25 4]

УРАВНГНИЯ

ИМПУЛЬСНЫХ

CHCTFM

371

где

k(mT)

—

оригинал, соответствующий изображению

/(*(/?).

Исходя из уравнения относительно изображений (25 13), на ос-

новании

теоремы свертывания получим уравнение импульсной

системы относительно оригиналов:

171

(щТ)

{sT)

({m

s) T)

(25.14)

или,

что

эквивалентно,

(

пг

т)

((m -~s)T)f

{sT).

(25.15)

Эти уравнения определяют процессы в замкнутой импульсной си-

стеме при произвольном внешнем воздействии

f(mT)

В отличие

от уравнения (23

22),

определяющего процесс в импульсной си-

стеме через временную характеристику разомкнутой системы в

неявной

форме, уравнения (25.14), (25 15) определяют процесс

импульсной системе через временную характеристику замкну-

той системы в явной форме. Нетрудно видеть, что выражения

(25.14),

(25.15)

являются решением уравнения (23 22).

Предположим, что внешнее воздействие кратковременно, т. е.

]

^>o!

(25Л6)

Тогда

из

уравнения

(25

15) получаем

{mT)

^=Zk({m-s)T)(y

(sT)

(mT),

откуда

следует,

что реакция замкнутой импульсной системы на

импульсное решетчатое воздействие определяется временной ре-

шетчатой функцией k{mT)

.Назовем

k(mT)

временной

характери-

стикой

замкнутой импульсной

системы

Найдем явное выражение

для временной характеристики. Передаточная функция замкну-

той импульсной системы равна

7i|ri-

25Л7

где

и Р* —

многочлены

по

рТ

степени

лип

— 1

соответ-

ственно. Подставляя

W*(p) в (25

17),

получим

к-it,)-

{р)

Q«

(Р

)

/>(,)

—

а*

(р)

•