Цыпкин Я.З Основы теории автоматических систем

Подождите немного. Документ загружается.

342

УРАВНЕНИЯ

ИМПУЛЬСНЫХ

СИСТЕМ

[ГЛ.

Индекс

«н» напоминает, что речь здесь идет об исходной непре-

рывной

части системы. Таким образом, уравнение непрерывной

части может быть записано в виде

(/)

(т)

y(t —

либо

где

(p) =.

Помимо

временной характеристи-

ки

(t)

и передаточной функции

(p),

линейная часть может быть

описана

и частотной характеристи-

кой

(/co),

которая получается из

Рис.

23.2. передаточной функции

W(p)

при за-

мене р на /со. Эти характеристики и

переменные указаны на рис. 23.2. Новым элементом в этой си-

стеме является импульсный элемент, и для составления уравне-

ния

всей системы в целом нам необходимо выяснить свойства

импульсного элемента и найти его уравнения.

23.2.

Импульсный

элемент

и его

уравнения

Амплитудно-импульсный элемент представляет собой устрой-

ство, реагирующее на дискретные равноотстоящие

друг

от дру-

га значения входного сигнала x(t) при t = mT. Его выходная

величина является последовательностью импульсов определенной

ФЩ

llllil.

HJLT

тггзг

OTZT3T

Рис.

23.3

формы,

амплитуда которых пропорциональна дискретным значе-

ниям

входной величины х(тТ) (рис. 23.3). Поскольку

мы

основном рассматриваем амплитудно-импульсные элементы, то

для краткости слово

«ахмплитудный»

мы

будем

опускать.

Назовем

простейшим

импульсным

элементом

такой, выход-

ная

величина которого x*{t) представляет собой последователь-

23.2]

ИМПУЛЬСНЫЙ

ЭЛЕМЕНТ

И ЕГО

УРАВНЕНИЯ

343

ность

б-функций,

«площади»

которых равны дискретным значе-

ниям

выходной величины

х(тТ).

Физически б-функции

(см. при-

ложение

соответствуют

импульсам бесконечно большой

ам-

плитуды

бесконечно малой длительности,

площадью,

рав-

ной

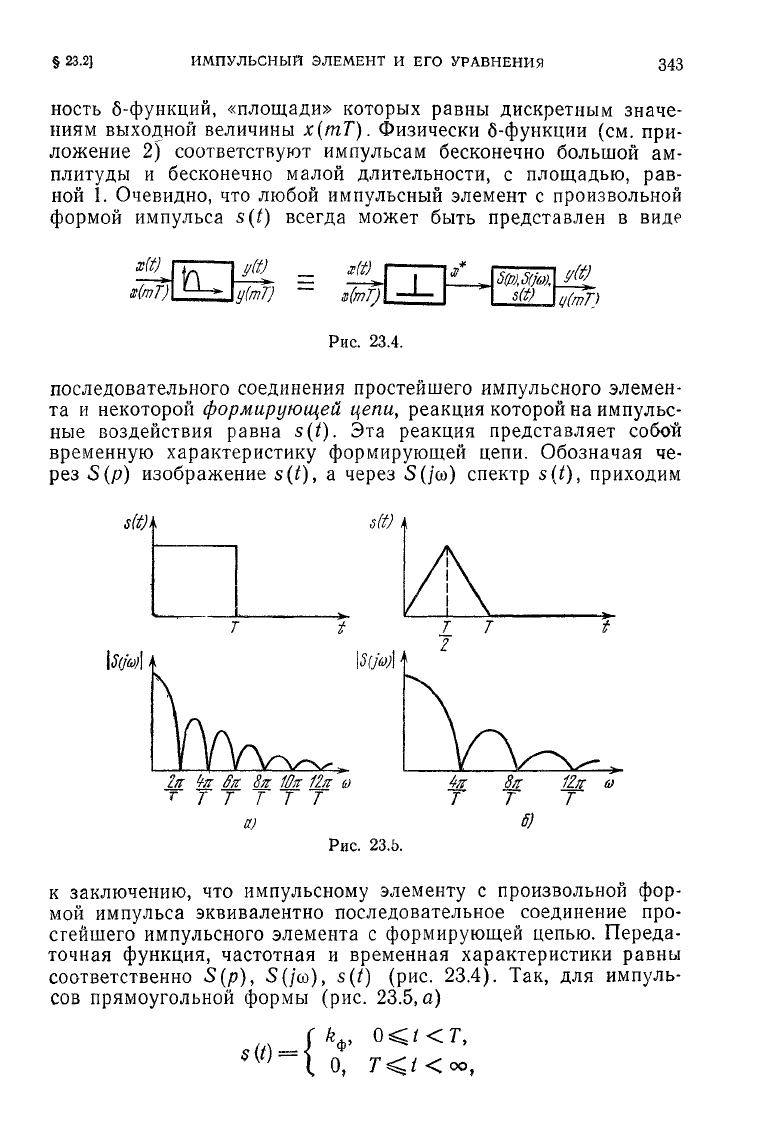
Очевидно,

что

любой импульсный элемент

произвольной

формой

импульса

s(t)

всегда

может быть представлен

виде

у(тГ)

p,(j

s(t)

Рис.

23.4.

последовательного соединения простейшего импульсного элемен-

та

некоторой

формирующей

цепи,

реакция которой

на

импульс-

ные

воздействия равна

s(t). Эта

реакция представляет собой

временную характеристику формирующей цепи. Обозначая

че-

рез

S(p)

изображение

s(t),

через

(/со) спектр

s(t),

приходим

sit)

s(t)

\5<ja)\

Ш Ш

Рис.

23.5.

заключению,

что

импульсному элементу

произвольной

фор-

мой

импульса эквивалентно последовательное соединение

про-

стейшего импульсного элемента

формирующей цепью. Переда-

точная функция, частотная

временная характеристики равны

соответственно

S(p),

S(/co),

s(t) (рис.

23.4).

Так, для

импуль-

сов прямоугольной формы

(рис. 23.5, а)

0</<7\

О,

Г</<оо

344

имеем

при р

/со

УРАВНЕНИЯ ИМПУЛЬСНЫХ СИСТЕМ [ГЛ. 23

sin

/со

(if-,

Для импульсов треугольной формы (рис. 23.5, б)

{

0</<

будем

иметь

а при р = /со

Г</<оо,

Заметим,

что для конечных по времени импульсов, т. е. для

финитных

s(t),

передаточная функция S(p) не имеет особых то-

чек

— полюсов. Формирующие цепи можно отнести к непрерыв-

ной

части системы. Поэтому здесь мы ограничимся детальным

xlt)

x(mT)

Рис.

23.6.

изучением свойств и особенностей простейшего импульсного эле-

мента. Выходная величина простейшего импульсного элемента

x*(t)

представляет собой последовательность модулированных

6-функций, поэтому простейший импульсный элемент можно так-

же рассматривать как модулятор б-функций (рис. 23.6). Пред-

ставим немодулированную периодическую последовательность

б-функций в виде

Ь((-шТ)

23.2] ИМПУЛЬСНЫЙ ЭЛЕМЕНТ И ЕГО УРАВНЕНИЯ 345

либо представим эту периодическую последовательность в виде

ряда Фурье

2я

где

са

-у

частота квантования по времени.

Модуляция состоит в умножении входной величины — оги-

бающей—

x(t) на немодулированную последовательность

6г(/).

Следовательно, выходная величина простейшего импульсного

элемента

x*(t),

представляющая собой модулированную после-

довательность б-функций,

будет

равна

(23.1)

Изображение

непрерывной входной величины простейшего им-

пульсного элемента x(t) по определению равно

Найдем теперь изображение выходной величины простейшего

импульсного элемента

x*(t).

Учитывая (23.1), имеем

X* (р) = L {х*

(/)}

L {х

(/)

(/)}.

(23.2)

Если

подставить в

(23.2)

выражение

б?(0>

то мы

получим

оо оо

Х*(Р)=

L{x(t)6(t-mT)}=

x{mT)L{b{t-mT)}.

(23.3)

т—

—

оо

т=

—оо

Здесь учитывается то свойство б-функции, что, кроме точки

t =

тТ,

она

всюду

равна нулю. Замечая еще, что

оо

L{6(t — mT)}

6(t

—

mT)

e~p'

получаем из

(23.3)

Г(р)

Соотношение

(23.4)

отличается от

(23.2)

тем, что вместо не-

прерывных функций x(t) в нем фигурируют соответствующие ре-

шетчатые функции

х(тТ).

Поэтому соотношение

(23.4)

уместно

назвать дискретным преобразованием Лапласа или, короче,

346

УРАВНЕНИЯ

ИМПУЛЬСНЫХ

СИСТЕМ

[ГЛ. 23

D-преобразованием.

Итак, из

(23.4)

(23.2)

заключаем, что пре-

образование Лапласа, или

L-преобразование,

модулированной

последовательности б-функций равно дискретному преобразова-

нию

Лапласа, или

D-преобразованию,

соответствующей решет-

чатой функции

х(тТ),

т. е.

Подставляя в

(23.2)

выражение

бг(/)

через ряд Фурье, получим

оо

**<Р)=~

l*{x(t)ei*°*},

k=*~

оо

но

на основании свойств преобразования Лапласа

Ь{х{{)е!

Х{р-]1гщ).

Следовательно,

оо

£ £

(23.5)

Соотношение

(23.5)

устанавливает связь

между

изображениями

непрерывной

Х(р) и решетчатой функций Х*(р). Будем назы-

вать операцию нахождения Х*(р) по

Х(р),

определяемую соот-

ношением

(23.5),

^-преобразованием.

Приведенные выше соот-

ношения

справедливы при выполнении условия

x(/)=G,

t^O,

Если

же при t = 0

х(О)фО,

то вместо

(23.4)

(23.5)

следует

пользоваться соотношениями

X* (р)

D{x

(mT)}

{mT)

e~P

(23.6)

Х(р-}кщ).

(23.7)

Основные теоремы и свойства D- и

©-преобразований

приведены

приложении 3.

Здесь мы ограничимся несколькими примерами.

Пример.

Пусть х (t)

e~"

и, значит, X (р) = —-:—. Найдем

изображе-

~г

иие

соответствующей решетчатой функции (рис. 23.7, а, б)

23.2]

ИМПУЛЬСНЫЙ ЭЛЕМЕНТ

ЕГО

УРАВНЕНИЯ

347

Согласно

(23.6)

оо

X*(

{e-

amT

}=:

~(а+р)

тТ

Пользуясь

формулой суммы геометрической прогрессии получим

<„)

{

Таким

образом,

Х*(р)

..D{e-

amT

}

- (23.8)

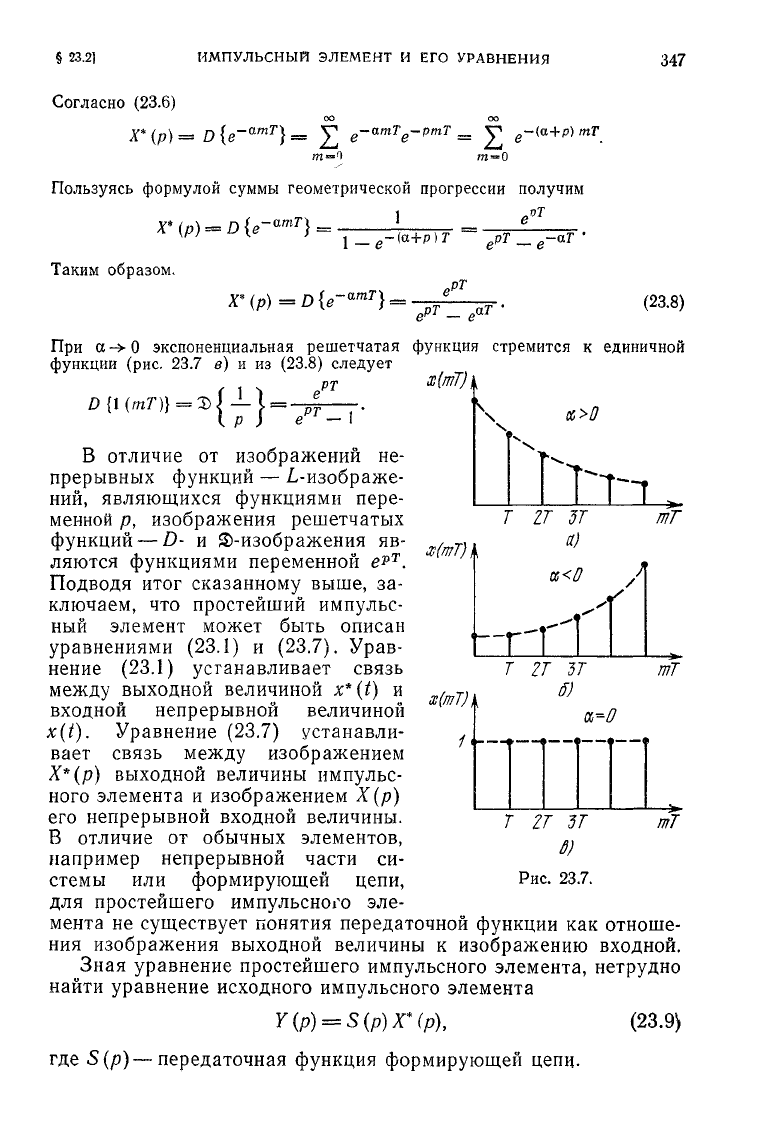
При

экспоненциальная решетчатая функция стремится

единичной

функции

(рис. 23.7 в) и из

(23.8)

следует

D{l(mT)}=^D<

{

их

)

Н1

—

ОС>0

В отличие

от

изображений

не-

прерывных функций

—

L-изображе-

ний,

являющихся функциями пере-

менной

/?,

изображения решетчатых

функций

— D-

©-изображения

яв-

ляются функциями переменной

е^

Подводя итог сказанному выше,

за-

ключаем,

что

простейший импульс-

ный

элемент может быть описан

уравнениями

(23.1)

(23.7). Урав-

нение

(23.1)

устанавливает связь

между

выходной величиной

x*(t) и

входной непрерывной величиной

x(t).

Уравнение

(23.7)

устанавли-

вает связь

между

изображением

Х*(р) выходной величины импульс-

ного элемента

изображением

Х(р)

его непрерывной входной величины.

В отличие

от

обычных элементов,

например

непрерывной части

си-

стемы

или

формирующей цепи,

для простейшего импульсного

эле-

мента

не

существует

понятия передаточной функции

как

отноше-

ния

изображения выходной величины

изображению входной.

Зная

уравнение простейшего импульсного элемента, нетрудно

найти

уравнение исходного импульсного элемента

Y(p)

S(p)r(p),

(23.9)

где

S(p)—передаточная

функция формирующей цепи.

тТ

Рис.

23.7.

348

УРАВНЕНИЯ

ИМПУЛЬСНЫХ

СИСТЕМ

(ГЛ. 23

23.3.

Свойства

импульсного

элемента

Выясним

спектральные, или частотные, свойства простейшего

импульсного элемента. Для этой цели воспользуемся его урав-

нением

относительно изображений (23.5). Для простоты мы по-

ложим, что имеет место условие

x(t)=O

при / < 0. Полагая

(23.5) р = /со, найдем связь между спектрами выходной и

входной величин простейшего импульсного элемента:

ОО

Г(/ю)

©{*(/«>)}=™

{«>

koo)).

(23.10)

&=•—

оо

Отсюда следует, что

спектр

X*(ja)

выходной

величины

x*(t)

простейшего

им-

пульсного

элемента

пропорционален

сумме

смещенных

спектров

X (/ (со —

k(x)o))

непрерывной

входной

величины

Заменим

в (23.10) со на со

гсо

где

—целое

число. Тогда

Вводя новую переменную

/-,

получим

&=»—

ОО

^ssr—OO

Таким

образом,

Г(/(со±гсо

))

Г(/со)

(23.11)

и, значит,

Из

соотношения

(23.11)

следует, что

спектр

X*(j<s))

выходной

величины

x*(t)

простейшего

им-

пульсного

элемента

периодичен

по

частоте

«периодом»,

равным

частоте

квантования.

Отсюда следует, что спектр

^*(/со)

полностью определяется

2~'

или в силу симметрии

(0,-о-J

Из

соотношения

(23.11)

следует,

чго

наличие в спектре входного

сигнала

А^(/со)

частоты

«i,

лежащей вне основной полосы

Y~'

"У")

вызывает

такой же эффект, как частота

coi

—

гсоо

где

— целое число такое, что |

со

—

гсо

| <

^т-,

т. е,

23.3!

СВОЙСТВА ИМПУЛЬСНОГО ЭЛЕМЕНТА

349

простейший

импульсный элемент осуществляет перенос, транс-

понирование

частот в основную полосу

^—у-,

-тг)

•

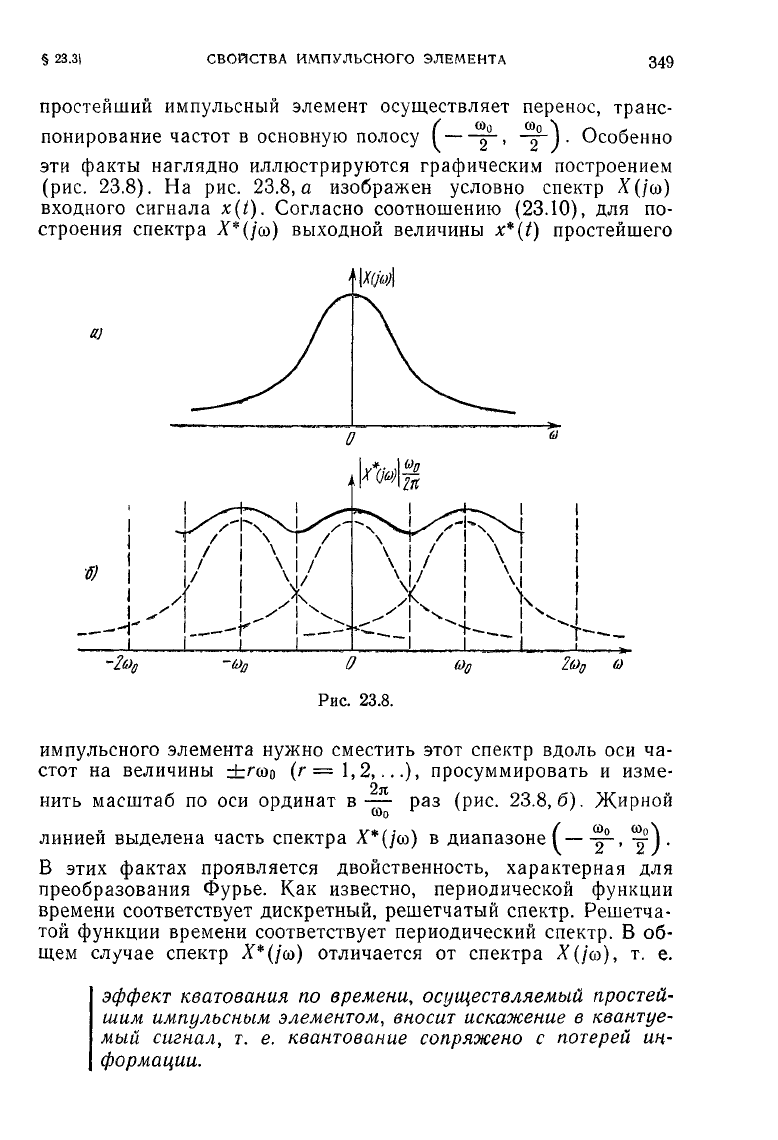
Особенно

эти

факты наглядно иллюстрируются графическим построением

(рис.

23.8). На рис. 23.8, а изображен условно спектр

Х(/со)

входного сигнала x(t). Согласно соотношению (23.10), для по-

строения

спектра

^*(/со)

выходной величины x*(t) простейшего

•s)

\l /

{

\X*P)

| /

| \

i i

1 1

>•**

Ztin

Рис.

23.8.

импульсного элемента нужно сместить этот спектр вдоль оси ча-

стот на величины

±поо

(г =

1,2,...),

просуммировать и изме-

нить

масштаб по оси ординат в— раз (рис.

23.8,6).

Жирной

линией

выделена часть спектра

Х*(/со)

в диапазоне

Г—-у-,

—V

В этих фактах проявляется двойственность, характерная для

преобразования Фурье. Как известно, периодической функции

времени соответствует дискретный, решетчатый спектр. Решетча-

той функции времени соответствует периодический спектр. В об-

щем

случае

спектр

^*(/(о)

отличается от спектра

X(ja>)

т. е.

эффект

кватования

по

времени,

осуществляемый

простей-

шим

импульсным

элементом,

вносит

искажение

в квантуе-

мый

сигнал,

т. е.

квантование

сопряжено

потерей

ин-

формации.

350

УРАВНЕНИЯ

ИМПУЛЬСНЫХ СИСТЕМ

[ГЛ. 23

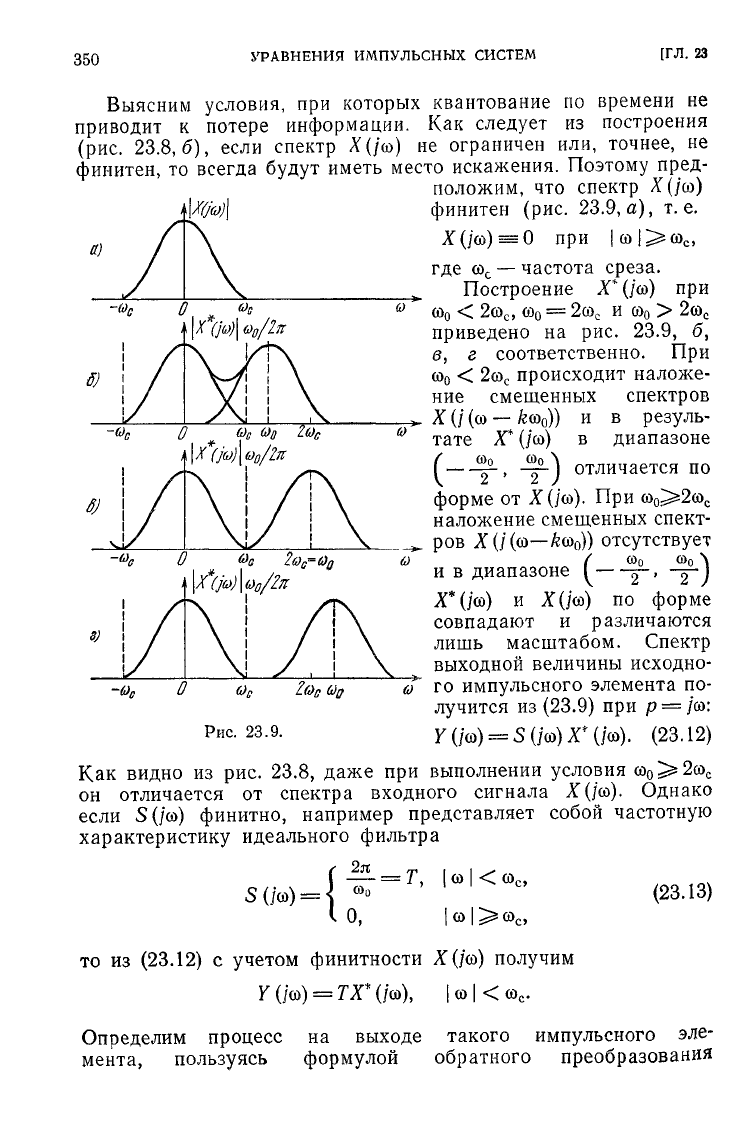
Выясним

условия, при которых квантование по времени не

приводит к потере информации. Как

следует

из построения

(рис.

23.8,6),

если спектр

Х(/оо)

не ограничен или, точнее, не

финитен,

то всегда

будут

иметь место искажения. Поэтому пред-

положим, что спектр

^(/со)

\X(jo))\

финитен (рис. 23.9, а), т.е.

(/©)

() ПрИ

|©|^©с,

где

— частота среза.

Построение

Т~

(/©)

при

©о

2©

©о

2©

©о

2©

приведено на рис. 23.9, б,

в, г соответственно. При

©о

2©

происходит наложе-

ние

смещенных спектров

&©о))

и в резуль-

тате

(/©)

в диапазоне

(—^-

}

-^-)

отличается по

форме от

Х(/©).

При

©о>2©

наложение смещенных спект-

ров

Х(/(©—&©о))

отсутствует

в диапазоне

<р,

-^М

X*(j®)

J(/©)

по форме

совпадают и различаются

лишь

масштабом. Спектр

выходной величины исходно-

__ __

fo^

го

импульсного элемента по-

лучится из

(23.9)

при р

/©:

ис

23.9.

(/©)

= S

(/©)

(/©).

(23.12)

Как

видно из рис. 23.8,

даже

при выполнении условия

>2©

он

отличается от спектра входного сигнала

X(j<£>)*

Однако

если

S(/©)

финитно, например представляет собой частотную

характеристику идеального фильтра

О,

|(0|>©с,

то из

(23.12)

учетом

финитности

Х(/©)

получим

к\х%Ъ)\о)

/2я

S(h)

- =

©с

(23.13)

(/©)

|©|<©

Определим процесс на

выходе

такого импульсного эле-

мента, пользуясь формулой обратного преобразования

§23.4]

УРАВНЕНИЯ ИМПУЛЬСНЫХ

АВТОМАТИЧЕСКИХ

СИСТЕМ

351

Фурье

которая

в силу (23.12),

(23.13)

принимает вид

У^^-k

^(/©)^dco.

(23.14)

-со

Но

из

(23.6)

при р

/со

следует,

что

m-l

Поэтому

из (23.14) получаем

(t)

(шТУ^-

е'»

С-"

"»

da,

m==l

или

окончательно

оо

sin

со

—

2/(0=

(t —

тТ)

откуда видно (рис. 23.9), как по дискретам х(тТ) восстанавли-

вается непрерывный сигнал без потери информации. Таким об-

разом,

если

непрерывная

величина

x(t)

обладает

финитным

спек-

тром

X(j(d)

частотой

среза

со

то

квантование

по

време-

ни ее с

частотой

со

2со

не

приводит

потере

инфор-

мации.

Этот вывод составляет содержание теоремы о квантовании и

лежит в основе импульсных способов передачи и преобразования

информации.

Она обосновывает возможность замены передачи

непрерывного сигнала передачей решетчатого сигнала без поте-

ри

информации. Для этого квантованный сигнал необходимо по-

дать на формирующее устройство, обладающее частотной харак-

теристикой идеального фильтра.

23.4. Уравнения импульсных автоматических

систем

Импульсную автоматическую ситему после замены импульс-

ного элемента соединением простейшего импульсного элемента и

формирующей цепи или формирующего устройства можно