Цыпкин Я.З Основы теории автоматических систем

Подождите немного. Документ загружается.

312

ПЕРИОДИЧЕСКИЕ

ПРОЦЕССЫ

[ГЛ.

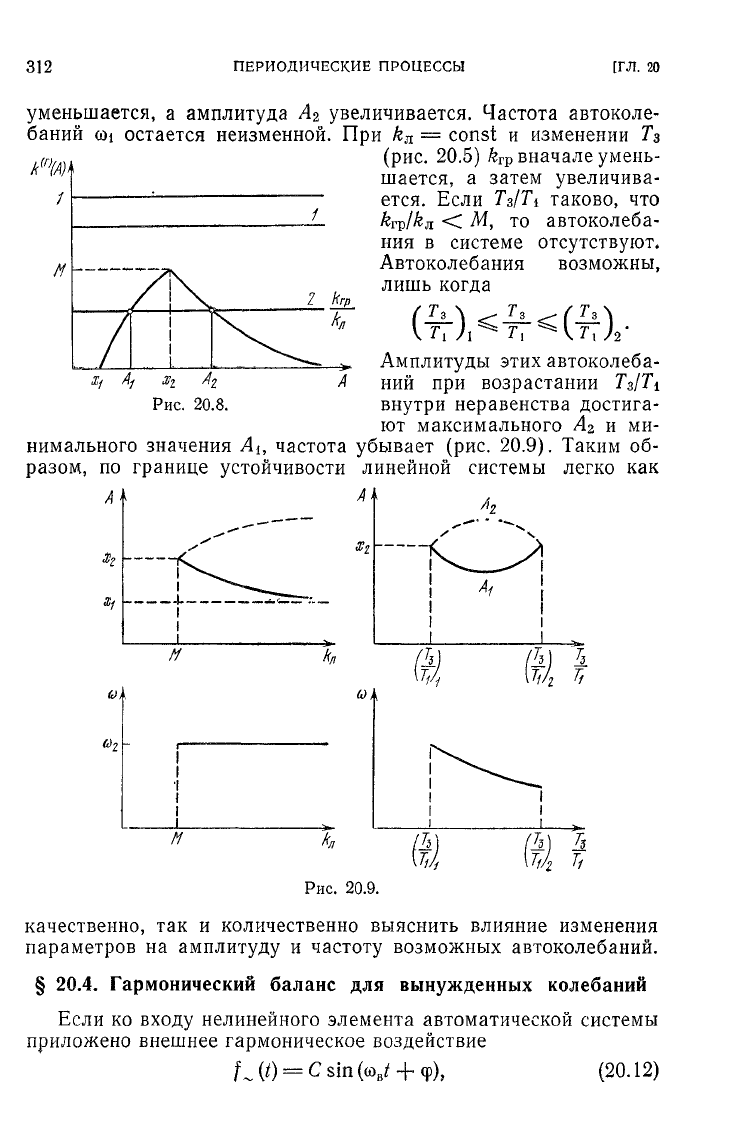
уменьшается, а амплитуда

увеличивается. Частота автоколе-

баний

coi

остается неизменной. При

= const и изменении

(рис.

20.5)

вначале умень-

шается, а затем увеличива-

ется. Если

Тз/Ti

таково, что

&гр/&л

М,

то автоколеба-

ния

в системе

отсутствуют.

Автоколебания возможны,

лишь

когда

(1)

(А)>

л,

Рис.

20.8.

пгр

Амплитуды

этих автоколеба-

ний

при возрастании

ТУА

внутри неравенства достига-

ют максимального

и ми-

нимального значения

Аи

частота

убывает

(рис. 20.9). Таким об-

разом,

по границе устойчивости линейной системы легко как

АЬ

Рис.

20.9.

качественно,

так и количественно выяснить влияние изменения

параметров на амплитуду и

частоту

возможных автоколебаний.

20.4.

Гармонический

баланс

для

вынужденных

колебаний

Если

ко

входу

нелинейного элемента автоматической системы

приложено внешнее гармоническое воздействие

(20.12)

§20 4] ГАРМОНИЧЕСКИЙ БАЛАНС ДЛЯ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ 313

то в зависимости от тех или иных условий в автоматической си-

стеме возможны различные режимы. Так, в абсолютно устойчи-

вых нелинейных системах вынужденные процессы

будут

перио-

дическими с частотой, равной частоте внешнего гармонического

воздействия

со

либо с частотами

со

субгармонических коле-

баний.

Если же в нелинейной системе были автоколебания, то

внешнее гармоническое воздействие может подавить эти автоко-

лебания,

навязав системе свою частоту

со

или

со

/&.

Мы пока

будем

интересоваться вынужденными процессами, которые при-

ближенно представляют собой гармонические колебания часто-

ты

со

т. е.

(20.13)

В комплексной форме записи

(20.12)

(20.13)

представляются

виде

(/)

(W4

(t)

Ае

(20.14)

Пользуясь уравнением гармонически линеаризованного нелиней-

ного элемента (20.3), можно записать уравнение вынужденного

процесса в комплексной форме:

оо

(t)

(/)

—

о,

(

)

£<г)

(А)

- т)

dx.

(20.15)

Замечая,

что

учитывая (20.14), получаем из

(20.15)

if) =

- W

(К)

|(D

(А)

(0,

(20.16)

или

1»

(/) =

L_^

{t)t

(

2o.i7)

1 + W

(/©

)

(

г)

(Л)

Уравнение

(20.17)

представляет собой уравнение относительно

ошибки

гармонически линеаризованной нелинейной системы, и

оно

может быть получено непосредственно по блок-схеме или

графу линеаризованной системы. Заменяя в

(20.16)

{t)

f^(t)

их значениями из (20.14), получим после сокращения на

основное

соотношение гармонического баланса для вынужден-

ных гармонических колебаний:

Се^

{A) AW

(/©

(20.18)

или

-£-

е/Ф

(/со

)

№

(Л).

(20.19)

314

ПЕРИОДИЧЕСКИЕ ПРОЦЕССЫ [ГЛ. 20

При

Е==

0 это соотношение переходит в соотношение гармони-

ческого баланса для автоколебаний.

Соотношение

гармонического

баланса

для

вынужденных

колебаний

(20.19)

определяет

амплитуду

вынужденных

колебаний

сдвиг

фаз

между

внешним

гармониче-

ским

воздействием

вынужденными

колебаниями.

Зависимость

ср

от частоты со внешнего воздействия опре-

деляет резонансные свойства нелинейной системы.

20.5.

Резонансные

свойства

нелинейной

автоматической

системы

Для исследования резонансных свойств воспользуемся соот-

ношением

гармонического баланса для вынужденных колебаний

(20.19). Его можно записать в виде

1(fa

)

(20.20)

АЬ

Г)

(А)

г)

(А)

или,

воспользовавшись обозначением

№

г)

{А) =

г)

(А)

е^

(Л)

{r)

(Л)

/е

(г)

(А)

(20.21)

Рассмотрим снова комплексную плоскость, на которой изобра-

жены частотная характеристика линейной части

W(/со)

и отри-

цательный обратный коэффициент гармонической линеаризации

—

з:

(рис.

20.10,

а)

под этой кривой. Отметим на частотной

{r)

(A)

характеристике линейной части

W(jco)

точку, соответствующую

частоте внешнего воздействия со =

со

Минимальное расстояние

^min(co

)

от этой точки до отрицательного обратного

коэффици-

ента гармонической линеаризации

—

определяется вели-

чиной

радиуса окружности с центром в точке со =

со

касаю-

щейся

—

—. Пусть это касание имеет место в точке

А=А

k^{A)

Тогда

(20.22)

)

{r)

)

Соотношение

(20.21) будет

выполнено

при

таких

со

и С, для

которых

(20.23)

20.5]

РЕЗОНАНСНЫЕ

СВОЙСТВА

НЕЛИНЕЙНОЙ

СИСТЕМЫ

315

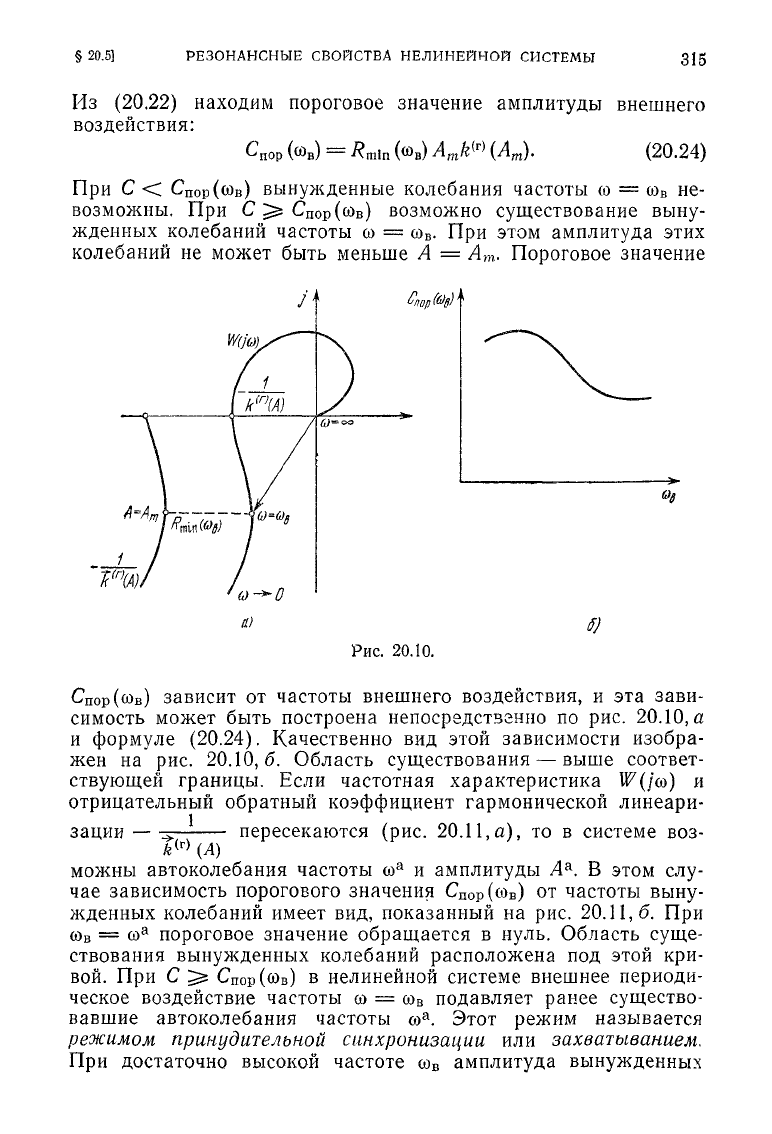
Из

(20.22)

находим пороговое значение амплитуды внешнего

воздействия:

Спор

(©в) =

Ятш

К)

№

(А

(20.24)

При

<С

Спор(сов)

вынужденные колебания частоты со =

со

не-

возможны. При

С^Спор(о)в)

возможно существование выну-

жденных колебаний частоты со =

со

При этом амплитуда этих

колебаний

не может быть меньше А =

Пороговое значение

Рис.

20.10.

р(в)

зависит от частоты внешнего воздействия, и эта зави-

симость может быть построена непосредственно по рис.

20.10,

формуле (20.24). Качественно вид этой зависимости изобра-

жен на рис.

20.10,6.

Область

существования

— выше соответ-

ствующей границы. Если частотная характеристика

W(j®)

отрицательный обратный коэффициент гармонической линеари-

зации

—

т£

пересекаются (рис.

20.11,а),

то в системе воз-

(г)

(А)

можны автоколебания частоты

со

и амплитуды

В этом слу-

чае зависимость порогового значения

ПО

р(со

)

от частоты выну-

жденных колебаний имеет вид, показанный на рис.

20.11,6.

При

о)

оз

пороговое значение обращается в нуль. Область суще-

ствования вынужденных колебаний расположена под этой кри-

вой.

При С ^

Спор(о)в)

в нелинейной системе внешнее периоди-

ческое воздействие частоты со =

со

подавляет ранее существо-

вавшие автоколебания частоты

оз

Этот режим называется

режимом

принудительной

синхронизации

или

захватыванием.

При

достаточно высокой частоте

со

амплитуда вынужденных

ПЕРИОДИЧЕСКИЕ

ПРОЦЕССЫ [ГЛ. 20

колебаний

С может быть сделана достаточно малой. Поэтому

часто при

сов

со

режим захватывания используется для по-

давления автоколебаний.

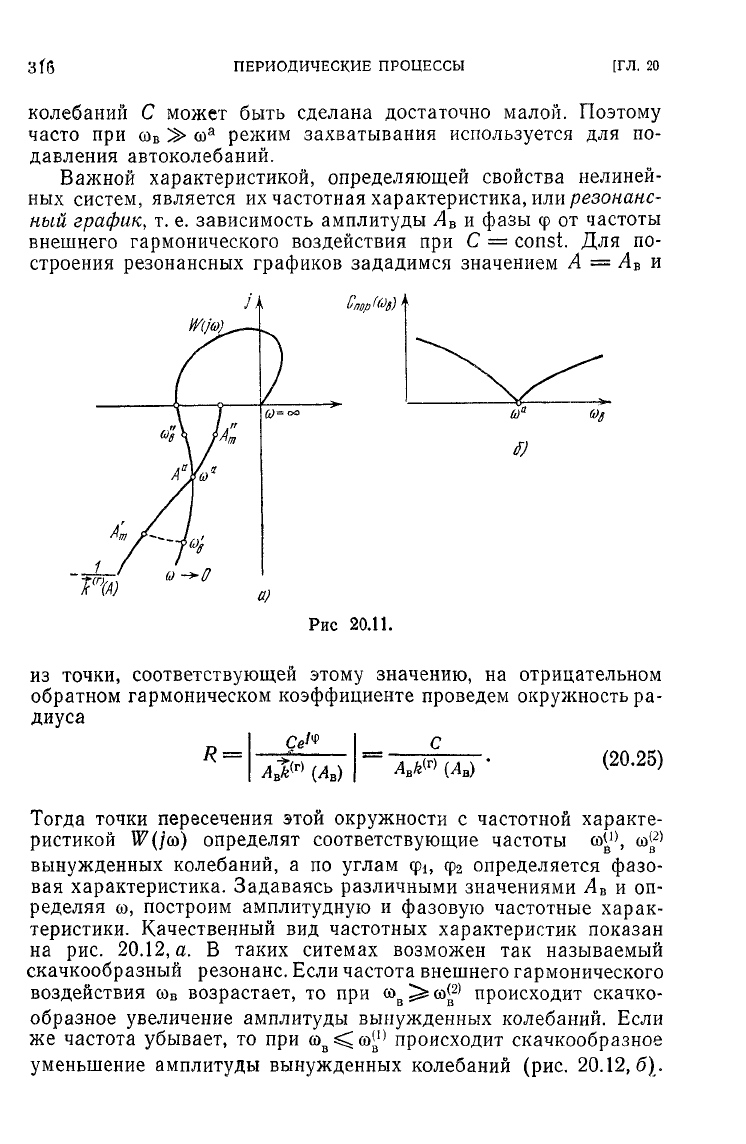
Важной характеристикой, определяющей свойства нелиней-

ных систем, является

их

частотная характеристика, или

резонанс-

ный

график,

т. е. зависимость амплитуды

фазы

ер

от частоты

внешнего гармонического воздействия при С = const. Для по-

строения

резонансных графиков зададимся значением А =

WIJQ)

Рис

20.11.

из

точки, соответствующей этому значению, на отрицательном

обратном гармоническом коэффициенте проведем окружность ра-

диуса

р/ф

(Л

)

(20.25)

Тогда точки пересечения этой окружности с частотной характе-

ристикой

!F(/co)

определят соответствующие частоты

со^,

ш^

вынужденных колебаний, а по

углам

определяется фазо-

вая

характеристика. Задаваясь различными значениями

и оп-

ределяя

оз,

построим амплитудную и фазовую частотные харак-

теристики.

Качественный вид частотных характеристик показан

на

рис.

20.12,

а. В таких ситемах возможен так называемый

скачкообразный

резонанс. Если частота внешнего гармонического

воздействия

оз

возрастает, то при

со

^со^

происходит скачко-

образное увеличение амплитуды вынужденных колебаний. Если

же частота убывает, то при

^о^

происходит скачкообразное

уменьшение амплитуды вынужденных колебаний (рис.

20.12,6).

20.5)

РЕЗОНАНСНЫЕ СВОЙСТВА НЕЛИНЕЙНОЙ СИСТЕМЫ

317

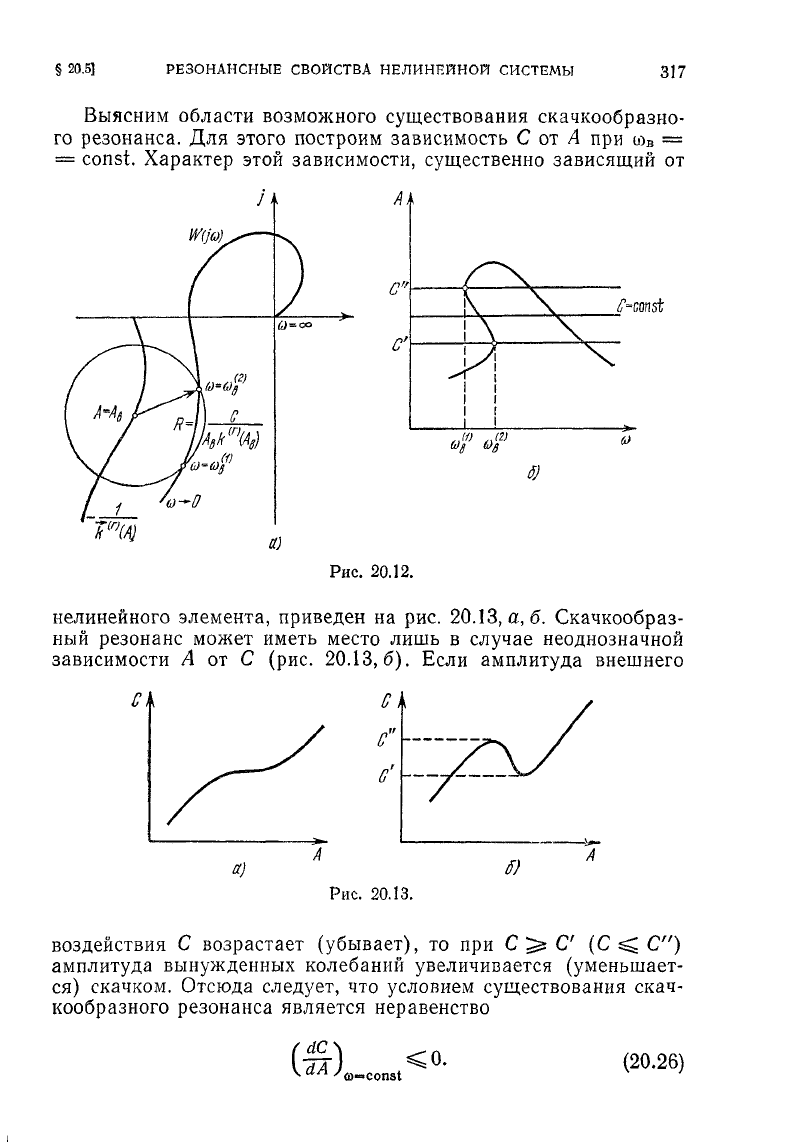
Выясним области возможного существования скачкообразно-

го резонанса.

Для

этого построим зависимость

С от Л при

(о

const. Характер этой зависимости, существенно зависящий

от

С'

..т

,.(2)

Рис.

20.12.

нелинейного элемента, приведен

на рис.

20.13,

а, б.

Скачкообраз-

ный

резонанс может иметь место лишь

случае

неоднозначной

зависимости

от С (рис.

20.13,6).

Если амплитуда внешнего

Рис.

20.13.

воздействия

возрастает (убывает),

то при С

(С

С")

амплитуда вынужденных колебаний увеличивается (уменьшает-

ся) скачком. Отсюда

следует,

что

условием существования скач-

кообразного резонанса является неравенство

(20.26)

318

ПЕРИОДИЧЕСКИЕ ПРОЦЕССЫ [ГЛ. 20

Раскроем

это условие для случая вещественного

коэффици-

ента гармонической линеаризации

№(А).

Запишем уравнение

(20.18)

в такой форме:

Се*

А№

(А)

[щ^

Отсюда находим, беря абсолютные величины от обеих частей,

А№

(A)

\(U

(ш)

ТПТТГУ

(со)]''

Дифференцируя обе части уравнения по Л, получим условие

существования скачкообразного резонанса в виде

(20.27)

На

плоскости частотной характеристики уравнение

(Л, со) = 0

соответствует окружности радиуса

с центром в точке

2 1 .

dkfr)

(

А\

и(?)

' '

Эти окружности зависят от амплитуды возможных вынужденных

колебаний.

Очевидно, что область возникновения скачкообраз-

ного резонанса определяется огибающей семейства окружностей.

Для получения уравнения огибающей в параметрической форме

достаточно продифференцировать по А

левую

часть

(20.27)

при-

равнять

результат

нулю и разрешить это уравнение относи-

тельно U и V. Тогда получим

dk^

(Л)

Т/

/м\

—

g/i

L_ dA

JV_

^Л

( }

г**

(г)

<^>

•

d2fe(r>

+Л

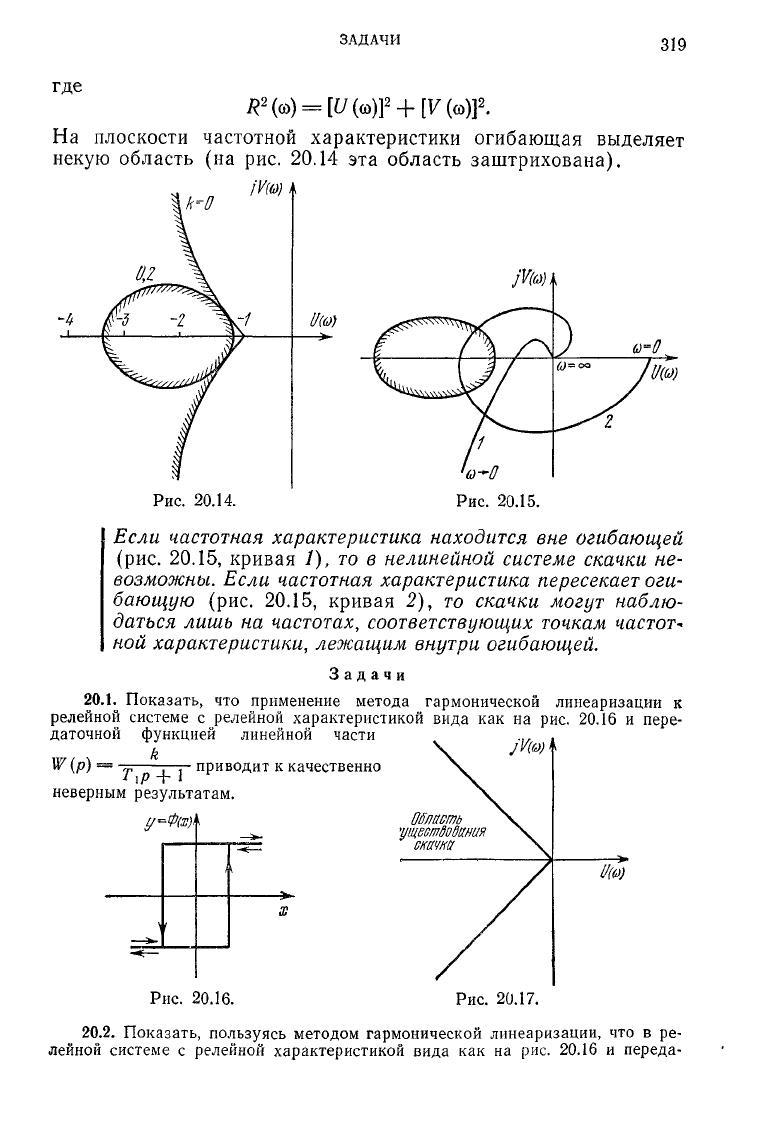
ЗАДАЧИ

319

где

На плоскости

частотной

характеристики

огибающая

выделяет

некую

область

(на рис. 20.14 эта

область

заштрихована).

/У(й>)

Рис.

20.14.

Рис.

20.15.

Если частотная характеристика находится вне огибающей

(рис.

20.15,

кривая

1),

то в нелинейной системе скачки не-

возможны. Если частотная характеристика пересекает оги-

бающую (рис. 20.15,

кривая

2), то скачки могут

наблю-

даться лишь на

частотах,

соответствующих точкам

частот*

ной

характеристики,

лежащим внутри огибающей.

Задачи

20.1.

Показать,

что

применение метода гармонической линеаризации

релейной

системе

релейной характеристикой вида

как на рис. 20.16 и

пере-

даточной функцией линейной части

(р) =

-=г

7-rr-

приводит

качественно

\р

неверным

результатам.

—*~

Я?

Рис.

20.16.

Рис.

20.17.

20.2. Показать, пользуясь методом гармонической линеаризации,

что в ре-

лейной

системе

релейной характеристикой вида

как на рис. 20.16 и

переда-

320 ПЕРИОДИЧЕСКИЕ ПРОЦЕССЫ

[ГЛ. 20

точной функцией линейной части W

(р)

у=

^—r-тт

частота и ампли-

р+

+ 1)

туда

возможных автоколебаний равны соответственно

20.3. Показать, что область существования резонансного скачка для си-

стемы с нелинейностью вида у

определяется условиями

— — —

V-.

2 !

Л2

' "~ "" з

Уз

или

(рис.

20.17).

Г л а $ а

СТОХАСТИЧЕСКИЕ

ПРОЦЕССЫ

21.1.

Особенности

стохастических

процессов

Стохастические процессы в нелинейных автоматических си-

стемах

могут

быть вызваны как внешними случайными воздей-

ствиями,

так и случайными изменениями параметров линейной

части или характеристики нелинейного элемента. Наличие нели-

нейного

элемента приводит к существенному изменению

плот-

ности

распределения

случайного процесса. Пусть ко

входу

не-

линейного

элемента приложено случайное воздействие

x(t),

плотность распределения которого в каждый момент времени t

гауссова (рис.

21.1,а),

т. е.

Ht)

р(*(О)

-т=-е

2а|

, (21.1)

где

а|

— дисперсия случайного

воздействия.

Среднее значение

случайного воздействия x(t) предполагается равным нулю. Плот-

ность распределения p(y(t)) выходной величины y(t) =

O(x(t))

будет,

вообще говоря, отличаться от p(x(t)) (21.1). Так, для

нелинейного

элемента с насыщением (рис.

21.1,6)

в интерва-

лах, где

|л;(£)|^и,о,

соответствующих линейным участкам с ко-

нечным

наклоном, отличным от нуля, распределение выходной

величины

будет

также гауссовым, при этом

\k\G

На

отрезках, где выходная величина постоянна, плотность распре-

деления y(t) является нулевой, с б-функциями на границе. Ве-

совые коэффициенты этих б-функций определяются из того

условия, что площадь любого распределения равна 1. Таким

образом, плотность распределения выходной величины y(t)

рассмотренного нелинейного элемента состоит из участков

гаус-

сова распределения и б-функций (рис. 21.1, б), т. е.

(У

(0)

гб

(у

(t)

kxo)

гб

(у (t) -

)

+ p (у)

|„

е(

ЛХо>

где

ко

-^—

[

V2JI

dx.

Я.

Цыпкин